CSDN 第三十一期竞赛题解
第二次参加
总分77.5,主要是在最后一题数据有误,花费了巨量时间…
参加的另一次比赛最后一道题目也出现了一点问题,有点遗憾。
题解
T1:最优利润值
你在读的经营课程上,老师布置了一道作业。在一家公司的日常运营中,是会对一些商品的价格走势根据一些经验和数据进行预估,并据此进行决策。例如,假设某商品每天的价格都有可能变动,我们要做的就是低买高卖获得最高利润。比如假设我们预估该商品接下来七天内的价格走势如下: 4 1 2 3 6 4 8 那我们采取的最佳策略是在价格1块钱的时候买入,在价格8块钱的时候卖出。为了简化整个过程,我们限定在此周期内只能有一次买入一次卖出,且商品在没有购入前是无法卖出的,即该商品不是期货而是现货。 现要求你用程序来实现自动决策。输入一定天数的商品预估价格,自动计算出最优利润值。例如,上面的例子中,最优利润值为8-1=7。(简单起见,只考虑0-100000之间的整数价格)
最大值 - 最小值即可,注意卖出时间比进货时间晚。
Code(时间复杂度小)
#include<bits/stdc++.h>
using namespace std;
int a[8],ans,mn=1e9;
int main(){for(int i=1;i<=7;i++){scanf("%d",a+i);mn=min(mn,a[i]);ans=max(ans,a[i]-mn);}printf("%d",ans);return 0;
}
T2:开学趣闻之美食诱惑
小艺酱又开学了,可是在上学的路上总会又各种意想不到的美食诱惑让小艺酱迟到。 假设小艺酱家到学校是一个n*n的矩阵。 每个格子包含一个诱惑值p,诱惑着小艺,让她迟到。 小艺位于矩阵的左上角,学校在矩阵的右下角落。 小艺想知道自己到达学校所要经历的最小诱惑值是?
数字三角形 dp 板题。
Code
#include<bits/stdc++.h>
using namespace std;
int n,a[5005][5005],f[5005][5005];
int main(){scanf("%d",&n);for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&a[i][j]);f[1][1]=a[1][1];for(int i=1;i<=n;i++) f[i][0]=f[0][i]=1e9;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j&&i==1) continue;f[i][j]=min(f[i-1][j]+a[i][j],f[i][j-1]+a[i][j]);}}printf("%d",f[n][n]);return 0;
}
T3:小艺照镜子
回文串是一个正读和反读都一样的字符串,已知字符串str。 输出字符串str中最长回文串的长度
CSDN竞赛题目短的题能难吗?
和前两题比起来,能。
Manacher板题。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=110005;
int cnt,len,ans,p[N<<1];
char s[N<<1],S[N],ch;
inline void Rd(){ans=0;s[0]='~';s[1]='|';len=strlen(S);for(int i=0;i<len;i++) s[i*2+2]=S[i],s[i*2+3]='|';cnt=strlen(s);return ;
}
int main(){while (~scanf("%s",S)){Rd();for(int t=1,r=0,mid=0;t<=cnt;t++){if(t<=r) p[t]=min(p[(mid<<1)-t],r-t+1);while (s[t+p[t]]==s[t-p[t]]) p[t]++;if(t+p[t]>r) r=t+p[t]-1,mid=t;if(p[t]>ans) ans=p[t];}printf("%d\n",ans-1);}return 0;
}
T4:爱吃鬼
小艺酱每天都在吃和睡中浑浑噩噩的度过。 可是小肚子是有空间上限v的。 小艺酱有n包零食,每包零食占据小肚子空间##a_i##并会给小艺酱一个甜蜜值##b_i##。 小艺酱想知道自己在小肚子空间上限允许范围内最大能获得的甜蜜值是多少?
题目描述是01背包?
而看数据应该是完全背包??
而交上去评测是???
别问我,我也不知道错哪儿了额。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL v,n,a[10005],b[10005],f[10000005];
int main(){scanf("%lld%lld",&v,&n);for(int i=1;i<=n;i++) scanf("%lld%lld",a+i,b+i);for(int i=1;i<=n;i++) for(int j=a[i];j<=v;j++) f[j]=max(f[j],f[j-a[i]]+b[i]);printf("%lld",f[v]);return 0;
}
找了一遍,最后一题的题解还是没有啊 @CSDN?
相关文章:

CSDN 第三十一期竞赛题解
第二次参加 总分77.5,主要是在最后一题数据有误,花费了巨量时间… 参加的另一次比赛最后一道题目也出现了一点问题,有点遗憾。 题解 T1:最优利润值 你在读的经营课程上,老师布置了一道作业。在一家公司的日常运营中&…...
)
EM_ASM系列宏定义(emscripten)
2.5 EM_ASM系列宏很多编译器支持在C/C代码直接嵌入汇编代码,Emscripten采用类似的方式,提供了一组以“EM_ASM”为前缀的宏,用于以内联的方式在C/C代码中直接嵌入JavaScript代码。2.5.1 EM_ASMEM_ASM使用很简单,只需要将欲执行的Ja…...

Batchnorm和Layernorm的区别
在深度学习训练中,我们经常会遇到这两个归一化操作,他们之间有什么区别呢?我们来简单介绍一下: BatchNorm: 在深度学习训练的时候我们的数据如果没有经过预处理,有可能会出现梯度消失或者梯度爆炸的情况&…...

高级前端面试题汇总
iframe 有那些优点和缺点? iframe 元素会创建包含另外一个文档的内联框架(即行内框架)。 优点: 用来加载速度较慢的内容(如广告)可以使脚本可以并行下载可以实现跨子域通信 缺点: iframe 会…...
HTML#5表单标签
一. 表单标签介绍表单: 在网页中主要负责数据采集功能,使用<form>标签定义表单表单项: 不同类型的input元素, 下拉列表, 文本域<form> 定义表单<input> 定义表单项,通过typr属性控制输入形式<label> 为表单项定义标注<select> 定义下拉列表<o…...

ONNX可视化与编辑工具
ONNX可视化与编辑工具netrononnx-modifier在模型部署的过程中,需要使用到ONNX模型,下面给大家推荐两个ONNX可视化与编辑工具,其中,netron仅支持模型的可视化,onnx-modifier支持ONNX的可视化与编辑。 netron Netron是…...
Verilog 学习第五节(串口接收部分)
小梅哥串口部分学习part2 串口通信接收原理串口通信接收程序设计与调试巧用位操作优化串口接收逻辑设计串口接收模块的项目应用案例串口通信接收原理 在采样的时候没有必要一直判断一个clk内全部都是高/低电平,如果采用直接对中间点进行判断的话,很有可能…...
)
AIX系统常见漏洞修复(exec、rlogin、rsh、ftp、telnet远端服务运行中)
漏洞:1.1 SSH 服务支持弱加密算法 1. 使用telnet 登录2.vi /etc/ssh/sshd_config 最后添加一下内容(去掉 arcfour、arcfour128、arcfour256 等弱加密算法) Ciphers aes128-ctr,aes192-ctr,aes256-ctr,aes128-cbc,3des-cbc,blowfish-cbc,cast…...
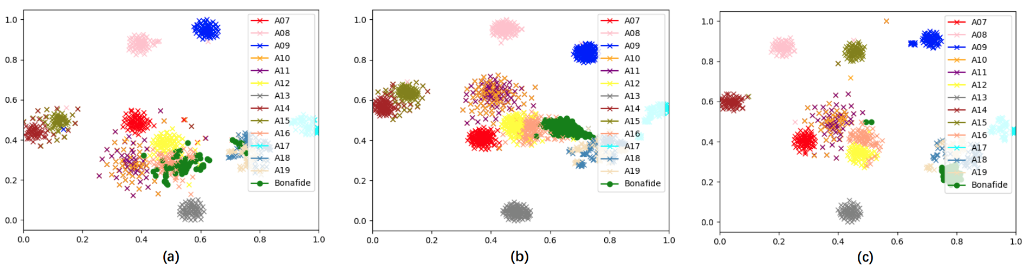
IEEE SLT 2022论文丨如何利用x-vectors提升语音鉴伪系统性能?
分享一篇IEEE SLT 2022收录的声纹识别方向的论文,《HOW TO BOOST ANTI-SPOOFING WITH X-VECTORS》由AuroraLab(极光实验室)发表。 来源丨AuroraLab AuroraLab源自清华大学电子工程系与新疆大学信息科学与工程学院,以说话人识别和…...
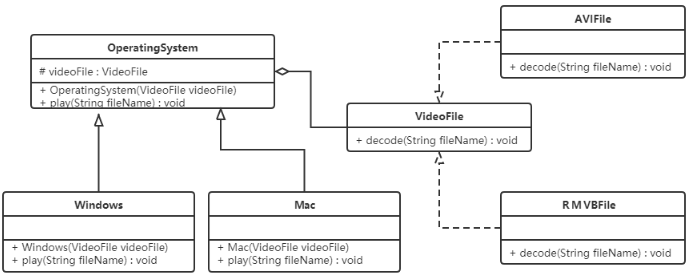
设计模式(十三)----结构型模式之桥接模式
1 概述 现在有一个需求,需要创建不同的图形,并且每个图形都有可能会有不同的颜色。我们可以利用继承的方式来设计类的关系: 我们可以发现有很多的类,假如我们再增加一个形状或再增加一种颜色,就需要创建更多的类。 试…...

倾向得分匹配案例分析
一、倾向得分匹配法说明 倾向得分匹配模型是由Rosenbaum和Rubin在1983年提出的,首次运用在生物医药领域,后来被广泛运用在药物治疗、计量研究、政策实施评价等领域。倾向得分匹配模型主要用来解决非处理因素(干扰因素)的偏差。 …...

基于SpringCloud的可靠消息最终一致性04:项目基础代码
上一节给出了项目需求和骨架代码,这一节来接着看基础代码。骨架代码和基础代码最主要的区别是:骨架代码都是数据库脚本、POM依赖文件、配置文件内容、运维脚本等,而基础代码则是和业务有关联,但并非关键代码的部分。 这些代码不用一个个地看,主要是看看结构就行。 图二十五…...

操作系统权限提升(十八)之Linux提权-内核提权
Linux 内核提权 Linux 内核提权原理 内核提权是利用Linux内核的漏洞进行提权的,内核漏洞进行提权一般包括三个环节: 1、对目标系统进行信息收集,获取到系统内核信息及版本信息; 2、根据内核版本获取其对应的漏洞以及EXP 3、使…...

华为OD机试真题Java实现【快递运输】真题+解题思路+代码(20222023
快递运输 题目 一辆运送快递的货车,运送的快递均放在大小不等的长方体快递盒中,为了能够装载更多的快递,同时不能让货车超载,需要计算最多能装多少个快递。 注:快递的体积不受限制,快递数最多1000个,货车载重最大50000。 🔥🔥🔥🔥🔥👉👉👉👉👉�…...

java面试题-JVM问题排查
1.常见的Linux定位问题的工具?常见的 Linux 定位问题的命令可以分为以下几类:系统状态命令:包括 top、uptime、vmstat、sar 等命令,用于查看系统整体的状态,如 CPU 使用率、内存使用率、磁盘 I/O 等。进程状态命令&…...
市场上有很多低代码开发平台,不懂编程的人可以用哪些?
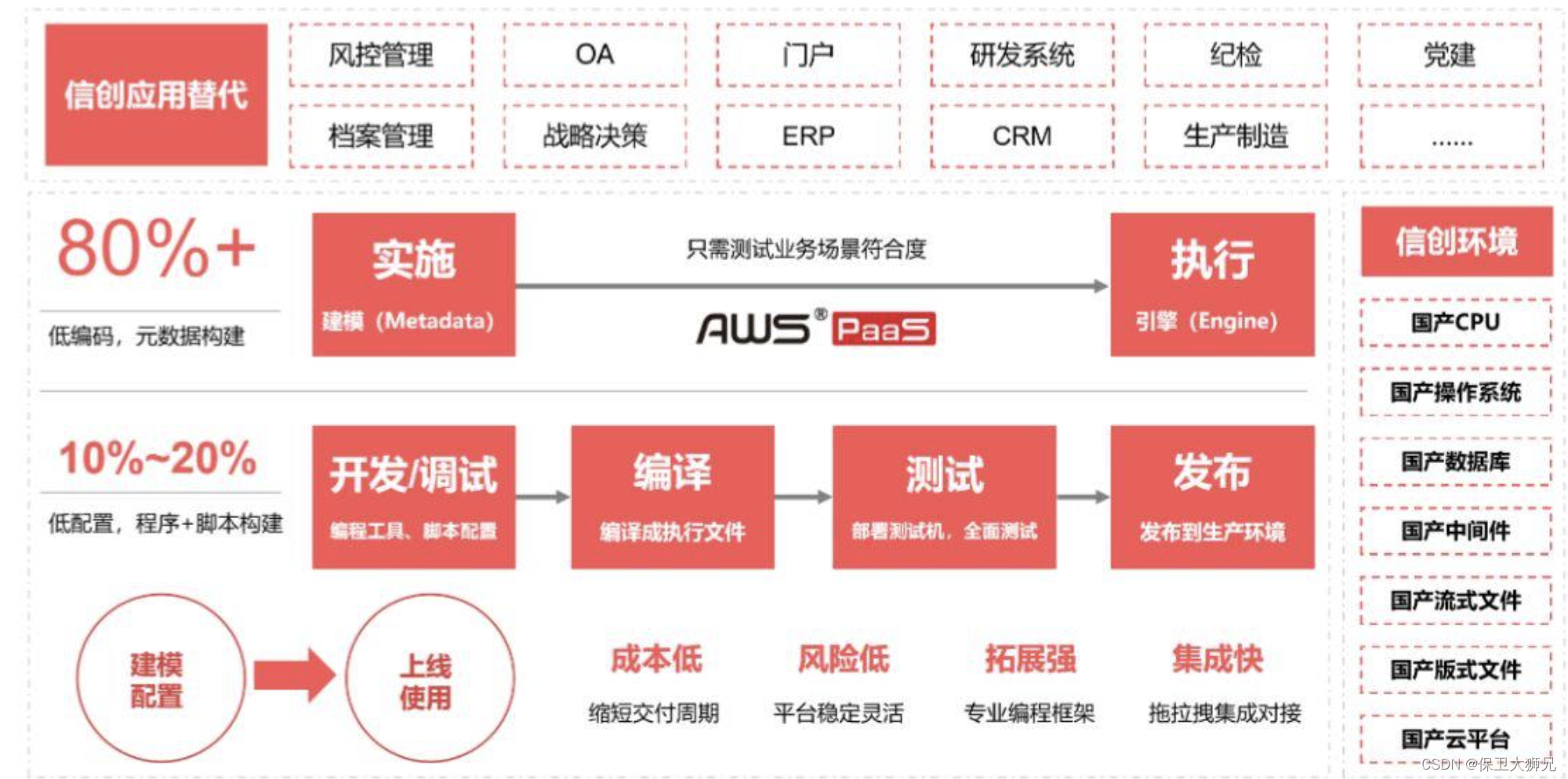
市场上有很多低代码开发平台,不懂编程的人可以用哪些?这个问题一看就是外行问的啦,低代码平台主打的就是一个“全民开发”,而且现在很多低代码平台都发展为零代码了,不懂编程也完全可以使用! 所谓低代码开…...

Tina_Linux打包流程说明指南_new
OpenRemoved_Tina_Linux_打包流程_说明指南_new 1 概述 1.1 编写目的 介绍Allwinner 平台上打包流程。 1.2 适用范围 Allwinner 软件平台Tina v3.0 版本以上。 1.3 相关人员 适用Tina 平台的广大客户,想了解Tina 打包流程的开发人员。 2 固件打包简介 固件…...

JVM面试题
JVM 1.jvm的组成部分 类加载器:将javac编译的class文件加载到内存中 运行时数据区:将内存划分成若干个不同的区域。 执行引擎:负责解析命令,提交操作系统执行。 本地接口:融合不同的语言为java所用 2.运行时数据区 方法区&…...

@FeignClient注解
1.在启动类上开启Feign功能 不开会提示找不到所需要的bean Consider defining a bean of type in your configuration SpringBootApplication EnableFeignClients public class AuthApplication {public static void main(String[] args) {SpringApplication.run(AuthApplic…...
一文搞懂如何在 React 中使用 防抖(Debounce)和 节流(Throttle)
在前端的日常开发中,经常会使用到两个函数防抖(Debounce)和节流(Throttle),防抖函数可以有效控制在一段时间内只执行最后一次请求,例如搜索框输入时,只在输入完成后才进行请求接口。…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
