@FeignClient注解
1.在启动类上开启Feign功能
不开会提示找不到所需要的bean
Consider defining a bean of type in your configuration@SpringBootApplication
@EnableFeignClients
public class AuthApplication {public static void main(String[] args) {SpringApplication.run(AuthApplication.class, args);}}2.编写Feign客户端:
@FeignClient(value = "checkcode" ,fallbackFactory = CheckCodeClientFactory.class)
public interface CheckCodeClient {//来自checkcode模块,checkcodecontroller下的方法@PostMapping(value = "/verify")public Boolean verify(String key, String code);
}这个客户端主要是基于SpringMVC的注解来声明远程调用的信息,比如:
服务名称:checkcode
熔断降级:CheckCodeClientFactory
请求方式:POST(请求的方法是其他模块中已有的方法,此处的方法的签名体和被调用的方法的签名体一致)
请求路径:/verify
请求参数:key,code
返回值类型:布尔
这样,Feign就可以帮助我们发送http请求,无需自己使用RestTemplate来发送了。
3.熔断方法:
/*** @author YCL* @version 1.0* @description 熔断方法* @date 2023-02-27 15:41*/
@Slf4j
@Component
public class CheckCodeClientFactory implements FallbackFactory<CheckCodeClient> {@Overridepublic CheckCodeClient create(Throwable throwable) {return new CheckCodeClient() {@Overridepublic Boolean verify(String key, String code) {log.debug("调用验证码服务熔断异常:{}",throwable.getMessage());return null;}};}
}
trick:
如果熔断方法和feign执行失败的返回值一致的话,我们无法区别到底是熔断了,还是feign执行失败了。所以此处return 的是null。而不是布尔类型,注意feign的verify方法的返回值是布尔类型。
相关文章:

@FeignClient注解
1.在启动类上开启Feign功能 不开会提示找不到所需要的bean Consider defining a bean of type in your configuration SpringBootApplication EnableFeignClients public class AuthApplication {public static void main(String[] args) {SpringApplication.run(AuthApplic…...
一文搞懂如何在 React 中使用 防抖(Debounce)和 节流(Throttle)
在前端的日常开发中,经常会使用到两个函数防抖(Debounce)和节流(Throttle),防抖函数可以有效控制在一段时间内只执行最后一次请求,例如搜索框输入时,只在输入完成后才进行请求接口。…...

Airbyte API
Airbyte API涵盖了Airbyte功能的方方面面,主要分类:Source_definition:来源定义,实现了来源的增删改查功能。Destination_definition:目标定义,实现了目标的增删改查功能。Workspace:工作区管理…...

vue项目使用Electron开发桌面应用
添加npm配置避免安装Electron错误 请确保您的 node 版本大于等于 18. cmd运行: npm config edit 该命令会打开npm的配置文件,请在空白处添加: electron_builder_binaries_mirrorhttps://npmmirror.com/mirrors/electron-builder-binaries/ e…...

std::chrono笔记
文章目录1. radio原型作用示例2. duration原型:作用示例3. time_point原型作用示例4. clockssystem_clock示例steady_clock示例high_resolution_clock先说感觉,这个库真恶心,刚接触感觉跟shi一样,特别是那个命名空间,太…...

接收arp请求并发送回应的实例
本文简单介绍了arp协议,用一个实例查看收到的ARP请求,并对该请求发出ARP回应,实例有完整的源代码,使用C语言在Linux下实现,代码中有详细的注释。 1. ARP协议 ARP(Address Resolution Protocol),地址解析协议;在局域网上通过IP地址获取物理地址MAC的协议,该协议工作在数…...
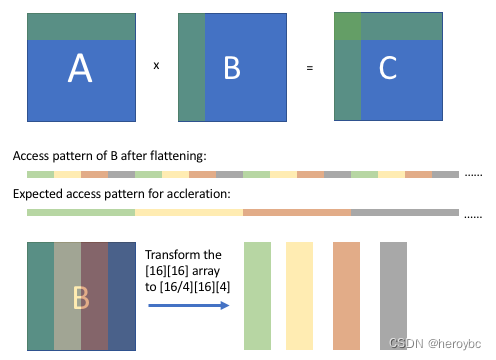
【高性能计算】TVM使用TE手动优化矩阵乘法算法解析与代码解读
引言 注:本文主要介绍、解释TVM的矩阵优化思想、代码,需要配合代码注释一起阅读。 矩阵乘法是计算密集型运算。为了获得良好的 CPU 性能,有两个重要的优化措施: 提高内存访问的高速缓存命中率。复杂的数值计算和热点内存&#x…...

消息中间件的概念
中间件(middleware)是基础软件的一大类,属于可复用的软件范畴。中间件在操作系统软件,网络和数据库之上,应用软件之下,总的作用是为处于自己上层的应用软件提供运行于开发的环境,帮助用户灵活、高效的开发和集成复杂的…...

窃密恶意软件Raccoon最新样本Stealer v2分析
Raccoon 是一个恶意软件家族,2019 年来一直在地下犯罪论坛中以恶意软件即服务的身份进行售卖。2022 年 7 月,该恶意软件家族发布了 C 语言编写的新版本 Raccoon Stealer v2,打破了以往使用 C 开发的传统。 Raccoon 是一个信息窃密恶意软件&a…...
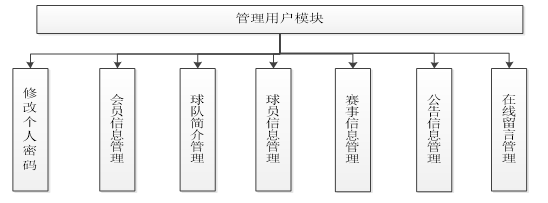
足球俱乐部管理系统
技术:Java、JSP等摘要:网站是一种主要的渠道。人们通过互联网快速、准确的发布信息、获取信息。而足球俱乐部是足球职业化、专业化的一个标志,是足球运动员以足球谋生时,所被聘用的机构,应运时代发展,规模、…...
)
2023上半年数学建模竞赛汇总(比赛时间、难易程度、含金量、竞赛官网)
1、美国大学生数学建模竞赛等级:国家级是否可跨校:否竞赛开始时间:2月17日~2月21日综合难度:⭐⭐⭐⭐ 竞赛含金量:⭐⭐⭐⭐⭐竞赛官网:https://www.comap.com/2、MathorCup高校数学建模挑战赛---大数据竞赛…...

【python学习笔记】:PHP7 Null合并运算符
在PHP7,一个新的功能,空合并运算符(??)已被引入。它被用来代替三元运算并与 isset()函数功能结合一起使用。如果它存在并且它不是空的,空合并运算符返回它的第一个操作数;否则返回第二个操作数。 示例 <?php// fetch the value of $_…...
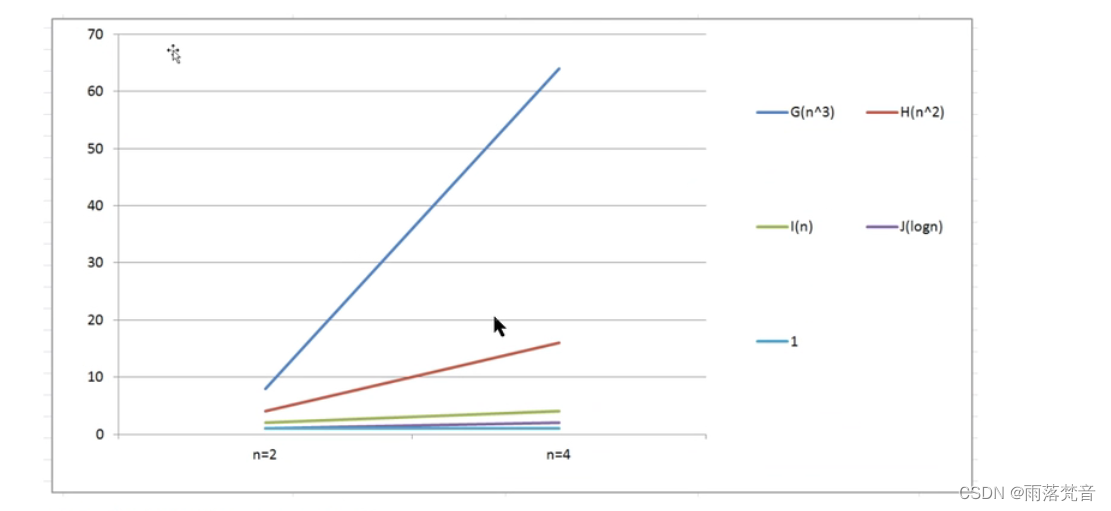
数据结构与算法——3.时间复杂度分析1(概述)
前面我们已经介绍了,研究算法的最终目的是如何花费更少的时间,如何占用更少的内存去完成相同的需求,并且也通过案例演示了不同算法之间时间耗费和空间耗费上的差异,但我们并不能将时间占用和空间占用量化。因此,接下来…...
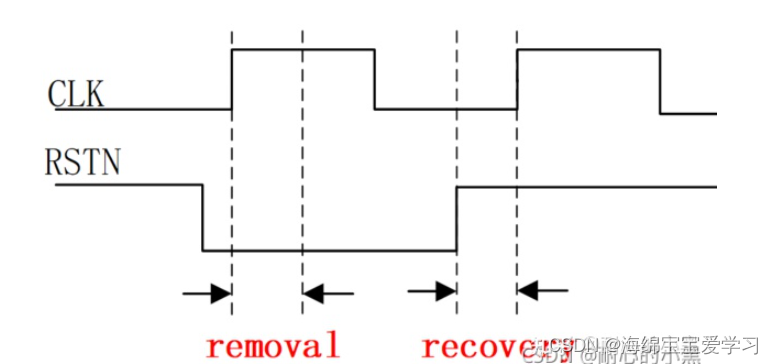
FPGA学习之日常工作复位电路
最近一个多月没有写博客了,然后最近工作中也遇到一个复位信号的问题。问题是这样的,关于外部复位信号,之前我们的处理方式都是通过PLL产生的Lock信号作为内部的复位信号。但是由于换到A54上面没有IP核,所以只有不用PLL,…...
)
【洛谷 P1177】【模板】快速排序 题解(快速排序+指针)
【模板】快速排序 题目描述 利用快速排序算法将读入的 NNN 个数从小到大排序后输出。 快速排序是信息学竞赛的必备算法之一。对于快速排序不是很了解的同学可以自行上网查询相关资料,掌握后独立完成。(C 选手请不要试图使用 STL,虽然你可以…...
Pthon--自动化实用技巧篇--文件目录处理
为什么要讲这一篇,主要是因为这个在自动化测试框架或者脚本的编写的时候会用到,还是比较方便的。看上述两个函数。getcwd()、chdir()。使用 os.getcwd() 函数获得当前工作目录。使用 os.chdir()函数改变当前工作目录。所以在用chdir()函数的时候别忘记指…...

想招到实干派程序员?你需要这种面试法
技术招聘中最痛的点其实是不精准。技术面试官或CTO们常常会向我们吐槽: “我经常在想,能不能把我们项目中的代码打印出来,作为候选人的面试题的一部分?” “能不能把一个Bug带上环境,让候选人来试试怎么解决…...

cesium常见操作:鼠标点击获取对象
目录 一、viewer.scene.pick(获取Cartesian2) 二、 viewer.scene.pickPosition(获取Cartesian3) 三、viewer.scene.drillPick(穿透拾取,获取所有对象) 四、viewer.scene.globe.pick…...
【玩转c++】git的安装和使用以及可视化处理
本期主题:git的安装和使用(windows环境)博客主页:小峰同学分享小编的在Linux中学习到的知识和遇到的问题 小编的能力有限,出现错误希望大家不吝赐1.两个工具介绍第一个工具git,链接gitee或者github等代码托…...

第三阶段02-Mybatis框架
Mybatis框架 Mybatis框架是目前最流行的数据持久层框架, 使用Mybatis框架可以帮助程序员自动生成JDBC代码, 程序员只需要通过注解或xml配置文件提供需要执行的SQL语句,以及对象和表的映射关系, Mybatis框架会根据此映射关系和SQL自动生成出JDBC代码,从而提高开发效率 Mybatis框…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
