WPF中的xmlns 和xmlns:x有什么区别?
WPF (Windows Presentation Foundation) 中的 xmlns 和 xmlns:x 是XML命名空间的声明,它们在XAML(eXtensible Application Markup Language)中被广泛使用。XAML是WPF、Silverlight、Xamarin.Forms等技术中用于定义UI元素的标记语言。
-
xmlns: 这是默认的XML命名空间。在WPF中,当你在XAML文件中使用xmlns,你通常指的是默认的WPF命名空间。这个命名空间包含了大多数常用的WPF控件和元素。例如:<Window xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"><!-- 这里是窗口内容 --> </Window>在这个例子中,
xmlns定义了一个范围,在这个范围内,你可以直接使用Button、TextBox等WPF控件,而无需指定额外的命名空间。 -
xmlns:x: 这是一个常用的前缀,用于引用XAML命名空间。这个命名空间包含了一些用于XAML处理的特殊功能,比如支持XAML的扩展和定义控件的键(Key)。最常见的用途是为XAML元素定义x:Name属性,这允许你在代码后面引用这些元素。<Window xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"><Button x:Name="myButton">Click Me</Button> </Window>在这个例子中,
xmlns:x声明了一个额外的命名空间,用于x:Name属性。这使得你可以在代码中通过myButton来引用这个按钮。
总的来说,xmlns和xmlns:x是XAML中用于区分不同功能和元素集的命名空间声明。xmlns通常用于默认的WPF元素,而xmlns:x用于XAML特有的功能和属性。
相关文章:

WPF中的xmlns 和xmlns:x有什么区别?
WPF (Windows Presentation Foundation) 中的 xmlns 和 xmlns:x 是XML命名空间的声明,它们在XAML(eXtensible Application Markup Language)中被广泛使用。XAML是WPF、Silverlight、Xamarin.Forms等技术中用于定义UI元素的标记语言。 xmlns: …...

为什么流量卡禁区多,而手机卡却可以用呢?
很多朋友比较关心流量卡禁区的问题,当我们申请流量卡时,运营商都会在套餐详情中标明具体的禁发地区,这个时候很多朋友都会有疑问了,为什么流量卡不能用的地区,可以申请到手机卡呢。 想要清楚这个问题࿰…...

Linux 桌面应用
Part I: Linux 系统概述 什么是 LinuxLinux 的历史和版本Linux 发行版介绍Linux 的优缺点 Part II: Linux 安装与配置 5. 硬件要求与准备工作 6. 安装 Linux 操作系统 7. Linux 系统初始化设置 8. Linux 系统更新与升级 9. Linux 基础配置 Part III: Linux 命令行 10. Linux…...

NLP领域的突破催生大模型范式的形成与发展
当前的大模型领域的发展,只是范式转变的开始,基础大模型才刚刚开始改变人工智能系统在世界上的构建和部署方式。 1、大模型范式 1.1 传统思路(2019年以前) NLP领域历来专注于为具有挑战性的语言任务定义和设计系统,…...
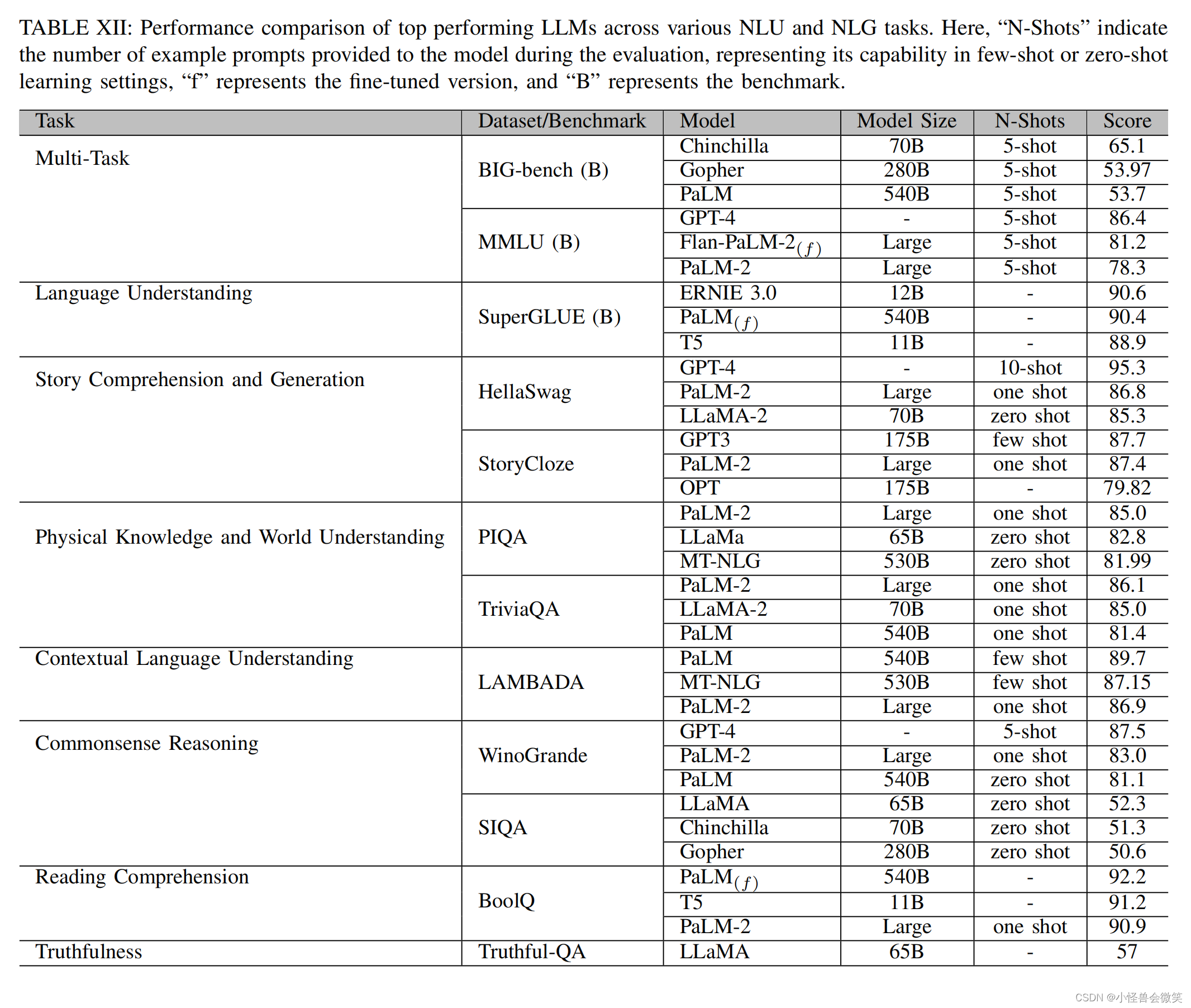
大模型的全面回顾,看透大模型 | A Comprehensive Overview of Large Language Models
大模型的全面回顾:A Comprehensive Overview of Large Language Models 返回论文和资料目录 论文地址 1.导读 相比今年4月的中国人民大学发表的大模型综述,这篇综述角度更侧重于大模型的实现,更加硬核,更适合深入了解大模型的一…...

【瑞禧分享】碳化硅纳米线 SiC纳米线 <100nm SiC晶须 SiC短纤维
碳化硅纳米线 规格或纯度:线/晶须含量:99% 供应商:西安瑞禧生物 英文名称:SiC Nanowire 别名:碳化硅纳米线,SiC晶须,SiC短纤维,SiC纳米线 英文别名:SiC Nanowire,SiC whiskers,SiC fiber 介绍&#x…...
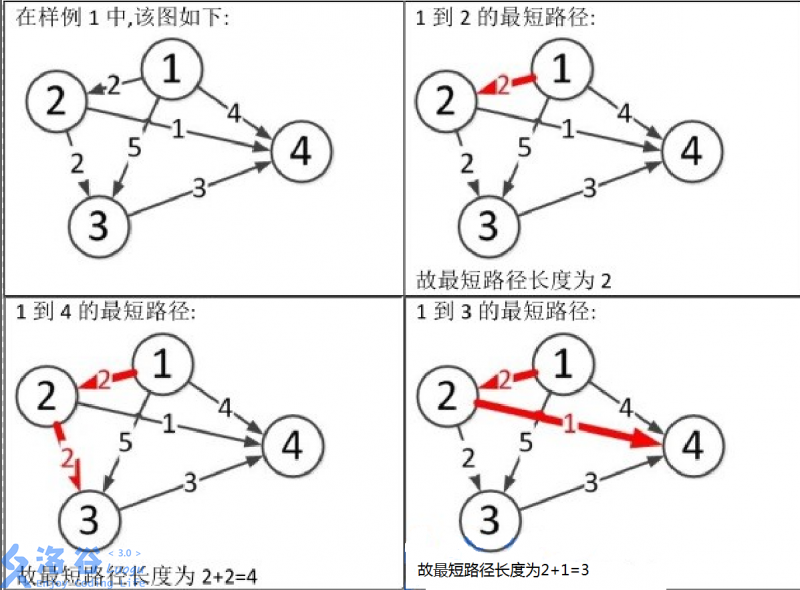
P3371 【模板】单源最短路径(弱化版)
【模板】单源最短路径(弱化版) 题目背景 本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步 P4779。 题目描述 如题,给出一个有向图,请输出从某一点出发到所有点的最短路…...
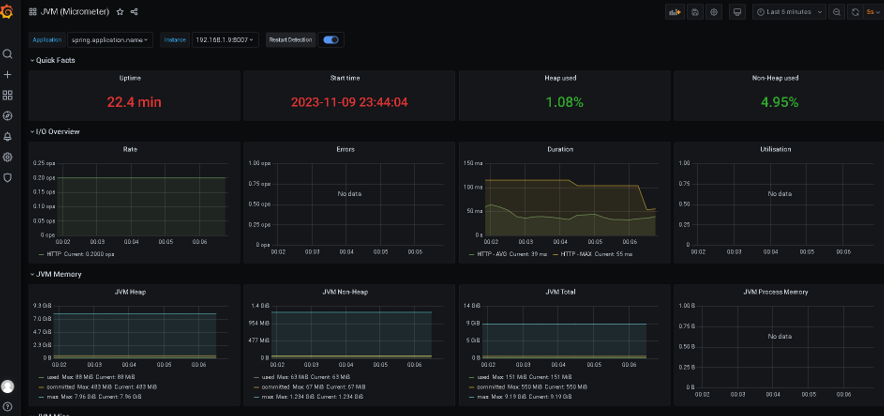
一文入门Springboot+actuator+Prometheus+Grafana
环境介绍 技术栈 springbootmybatis-plusmysqloracleactuatorPrometheusGrafana 软件 版本 mysql 8 IDEA IntelliJ IDEA 2022.2.1 JDK 1.8 Spring Boot 2.7.13 mybatis-plus 3.5.3.2 本地主机应用 192.168.1.9:8007 PrometheusGrafana安装在同一台主机 http://…...
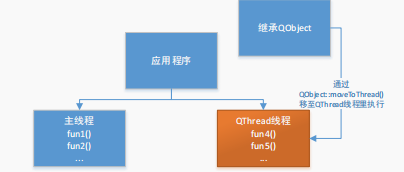
基于Qt 多线程(继承 QObject 的线程)
继承 QThread 类是创建线程的一种方法,另一种就是继承QObject 类。继承 QObject 类更加灵活。它通过 QObject::moveToThread()方法,将一个 QObeject的类转移到一个线程里执行。恩,不理解的话,我们下面也画个图捋一下。 通过上面的图不难理解,首先我们写一个类继承 QObj…...
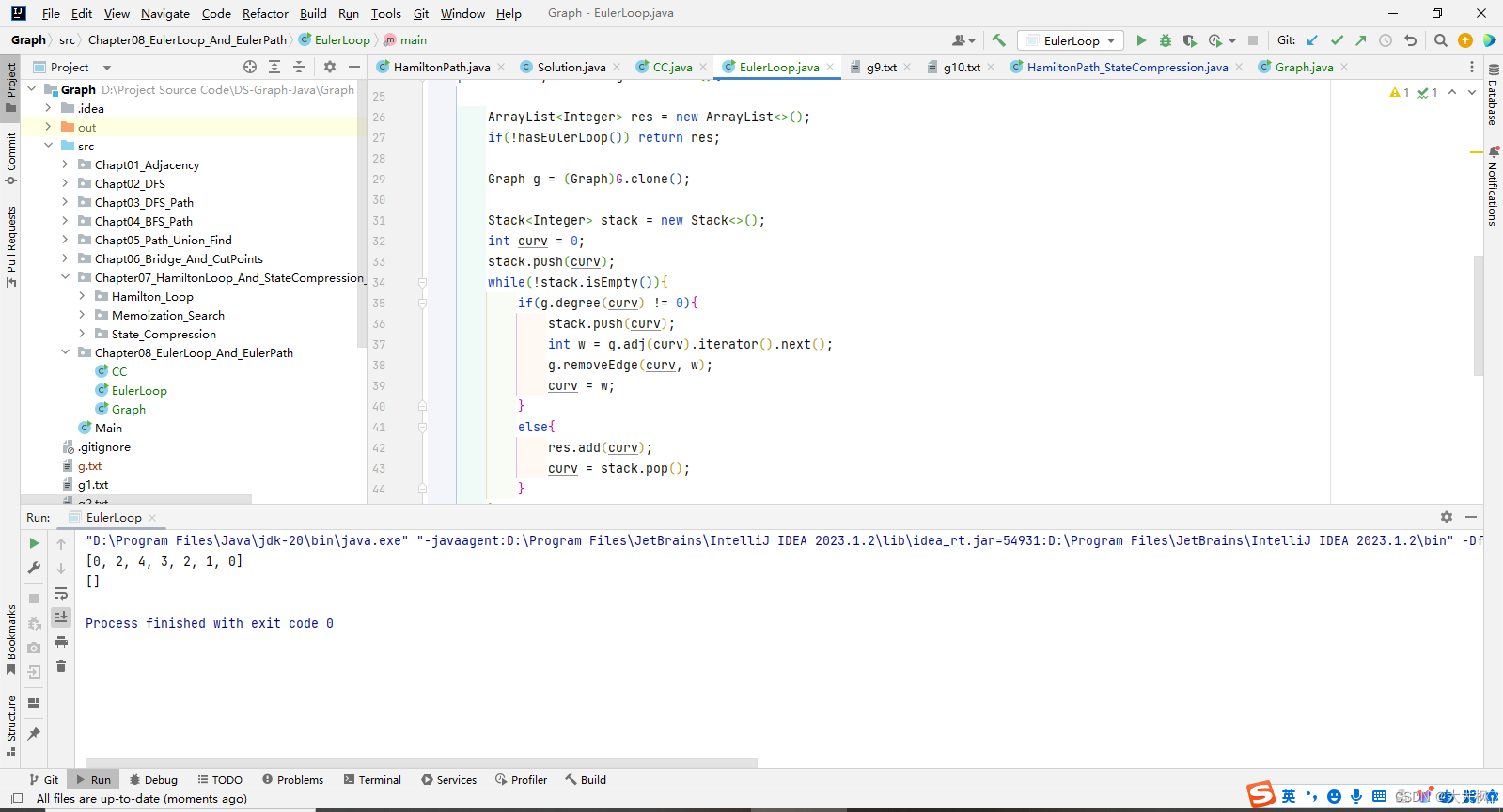
图论11-欧拉回路与欧拉路径+Hierholzer算法实现
文章目录 1 欧拉回路的概念2 欧拉回路的算法实现3 Hierholzer算法详解4 Hierholzer算法实现4.1 修改Graph,增加API4.2 Graph.java4.3 联通分量类4.4 欧拉回路类 1 欧拉回路的概念 2 欧拉回路的算法实现 private boolean hasEulerLoop(){CC cc new CC(G);if(cc.cou…...
(一)什么是Vite——vite介绍与使用
什么是Vite Vite(法语意为 "快速的",发音 /vit/,发音同 "veet")是一种新型前端构建工具,能够显著提升前端开发体验。 它主要由两部分组成: 一个开发服务器,它基于 原生 …...

直流电动机四象限运行控制变流器设计
摘 要 节能和效率是工业经济发展的主题,电机在各行各业都是主要的动力来源, 直流电机以其控制简单,效率高,功率密度大等优势脱颖而出。基于直流电动机四象限运行控制变流器应用广泛,比如电子设备、电机控制、工业等行…...
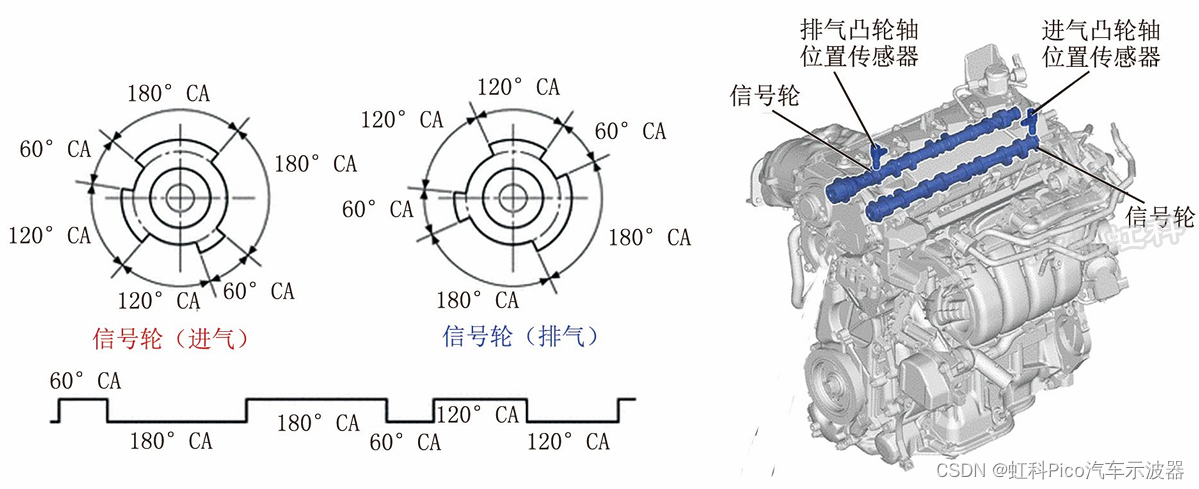
虹科示波器 | 汽车免拆检修 | 2021款广汽丰田威兰达PHEV车发动机故障灯异常点亮
一、故障现象 一辆2021款广汽丰田威兰达PHEV车,搭载A25D-FXS发动机和动力蓄电池系统(额定电压为355.2V,额定容量为45.0Ah),累计行驶里程约为1万km。车主反映,高速行驶时发动机突然抖动,且发动机…...

机器学习和深度学习领域的算法和模型
机器学习和深度学习领域有许多算法和模型,以下是一些常见的算法和模型: 线性回归(Linear Regression)逻辑回归(Logistic Regression)决策树(Decision Tree)随机森林(Ran…...

减轻关键基础设施网络安全风险的 3 种方法
物理安全和网络安全之间存在相当大的重叠,特别是在保护关键基础设施方面。防止基础设施被篡改需要在物理安全方面进行大量投资,但任何连接到互联网的设备都代表着更广泛网络的潜在攻击点。 缺乏足够保护的设备可能会给这些对手在网络中提供立足点&#…...

Redis的特性以及使用场景
分布式发展历程参考 陈佬 http://t.csdnimg.cn/yYtWK 介绍redis Redis(Remote Dictionary Server)是一个基于客户端-服务器架构的在内存中存储数据的中间件,属于NoSQL的一种。它可以用作数据库、缓存/会话存储以及消息队列。 作为一种内存数…...
【python后端】- 初识Django框架
Django入门 😄生命不息,写作不止 🔥 继续踏上学习之路,学之分享笔记 👊 总有一天我也能像各位大佬一样 🌝分享学习心得,欢迎指正,大家一起学习成长! 文章目录 Django入门…...

队列与堆栈:原理、区别、算法效率和应用场景的探究
队列与堆栈:原理、区别、算法效率和应用场景的探究 前言原理与应用场景队列原理应用场景: 堆栈原理应用场景递归原理和堆栈在其中的作用递归原理堆栈作用 队列与堆栈区别队列堆栈算法效率 前言 本文主要讲解数据结构中队列和堆栈的原理、区别以及相关的…...
数据结构与算法【链表:一】Java实现
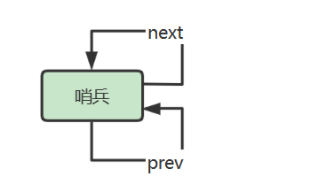
目录 链表 单向链表 哨兵链表 双向链表 环形链表 链表 链表是数据元素的线性集合,其每个元素都指向下一个元素,元素存储上并不连续。 随机访问性能 根据 index 查找,时间复杂度 O(n) 插入或删除性能 起始位置:O(1)结束位…...
数据结构 | 队列的实现
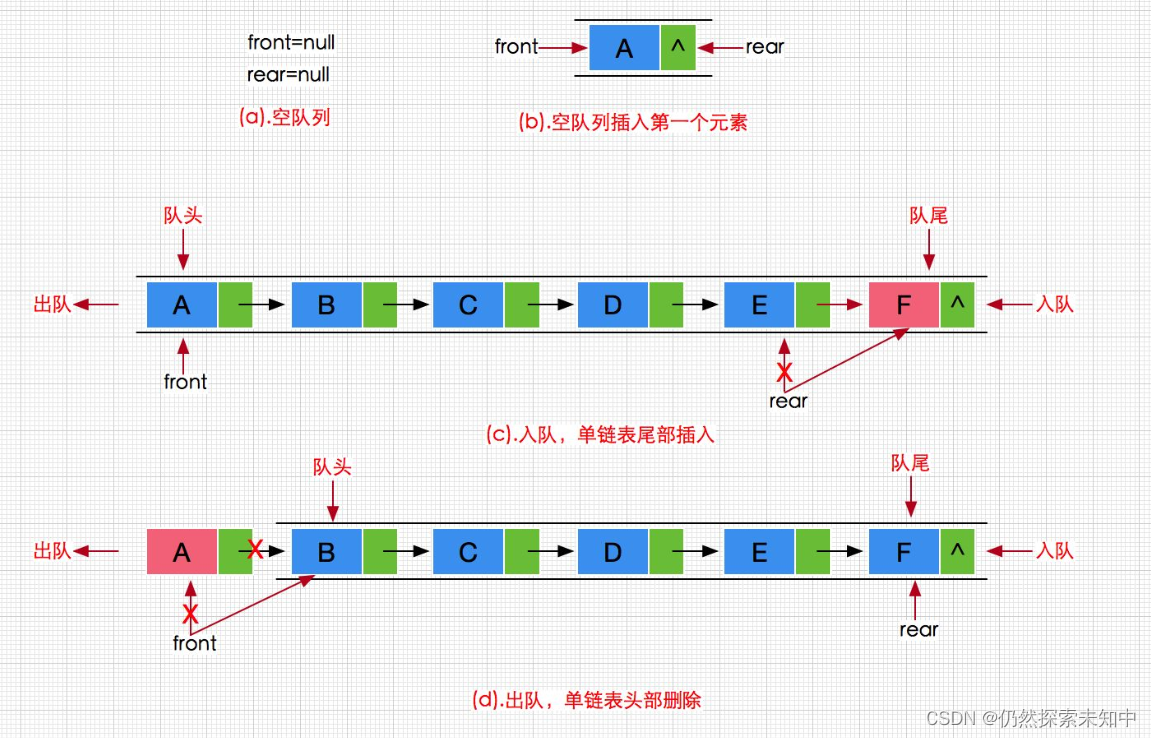
数据结构 | 队列的实现 文章目录 数据结构 | 队列的实现队列的概念及结构队列的实现队列的实现头文件,需要实现的接口 Queue.h初始化队列队尾入队列【重点】队头出队列【重点】获取队列头部元素获取队列队尾元素获取队列中有效元素个数检测队列是否为空销毁队列 Que…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
