代码随想录算法训练营第五十三天丨 动态规划part14
1143.最长公共子序列
思路
本题和动态规划:718. 最长重复子数组 (opens new window)区别在于这里不要求是连续的了,但要有相对顺序,即:"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
继续动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
有同学会问:为什么要定义长度为[0, i - 1]的字符串text1,定义为长度为[0, i]的字符串text1不香么?
这样定义是为了后面代码实现方便,如果非要定义为长度为[0, i]的字符串text1也可以,卡哥在 动态规划:718. 最长重复子数组 (opens new window)中的「拓展」里 详细讲解了区别所在,其实就是简化了dp数组第一行和第一列的初始化逻辑。
- 确定递推公式
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
代码如下:
if (text1.charAt(i-1) == text2.charAt(j-1)){dp[i][j] = dp[i-1][j-1]+1;
}else{dp[i][j] =Math.max(dp[i][j-1],dp[i-1][j]);
}
- dp数组如何初始化
先看看dp[i][0]应该是多少呢?
test1[0, i-1]和空串的最长公共子序列自然是0,所以dp[i][0] = 0;
同理dp[0][j]也是0。
其他下标都是随着递推公式逐步覆盖,初始为多少都可以,那么就统一初始为0。
代码:
int[][] dp = new int[text1.length()+1][text2.length()+1];- 确定遍历顺序
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图:
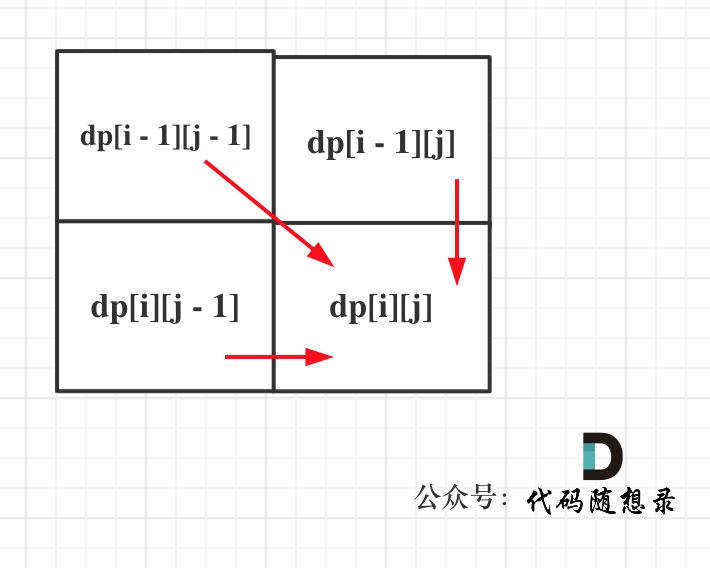
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵。
- 举例推导dp数组
以输入:text1 = "abcde", text2 = "ace" 为例,dp状态如图:
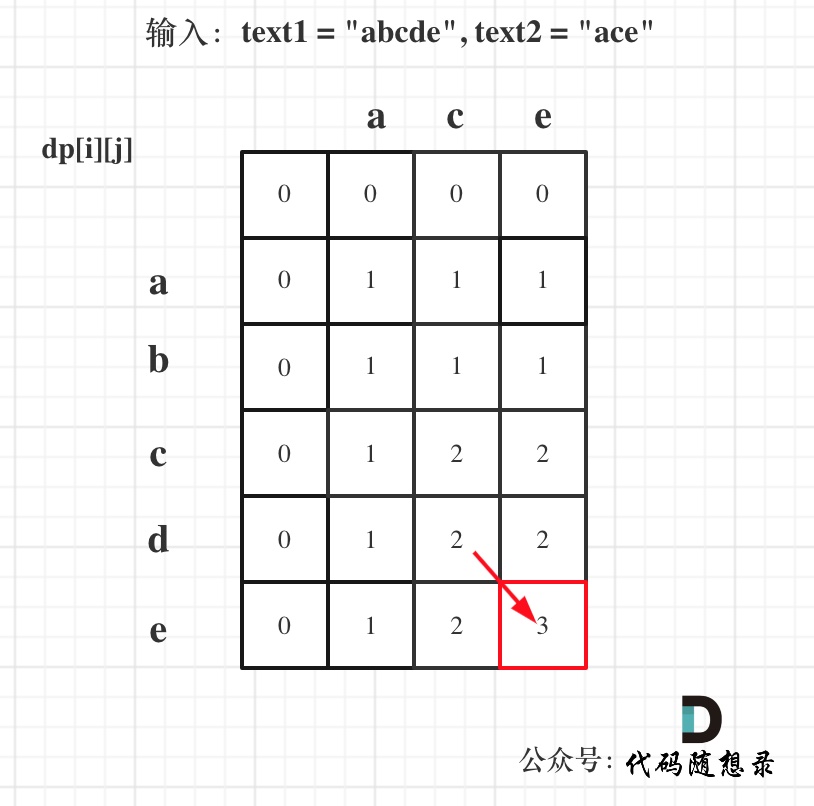
最后红框dp[text1.size()][text2.size()]为最终结果
以上分析完毕,C++代码如下:
class Solution {public int longestCommonSubsequence(String text1, String text2) {int[][] dp = new int[text1.length()+1][text2.length()+1];//Arrays.fill(dp,1);int result = 0;for (int i = 1; i <= text1.length(); i++) {for (int j = 1; j <= text2.length(); j++) {if (text1.charAt(i-1) == text2.charAt(j-1)){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] =Math.max(dp[i][j-1],dp[i-1][j]);}result = Math.max(result,dp[i][j]);}}return result;}
}- 时间复杂度: O(n * m),其中 n 和 m 分别为 text1 和 text2 的长度
- 空间复杂度: O(n * m)
1035.不相交的线
思路
相信不少录友看到这道题目都没啥思路,来逐步分析一下。
绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且直线不能相交!
直线不能相交,这就是说明在字符串A中 找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。
拿示例一A = [1,4,2], B = [1,2,4]为例,相交情况如图:
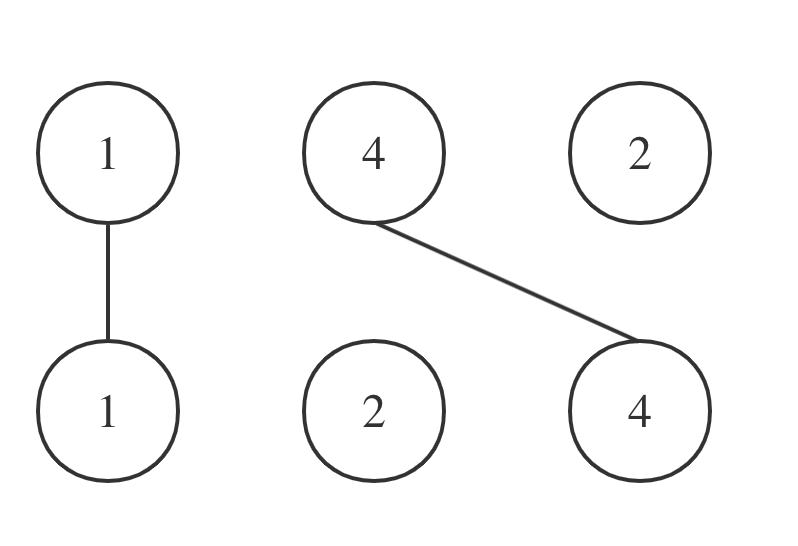
其实也就是说A和B的最长公共子序列是[1,4],长度为2。 这个公共子序列指的是相对顺序不变(即数字4在字符串A中数字1的后面,那么数字4也应该在字符串B数字1的后面)
这么分析完之后,大家可以发现:本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
那么本题就和我们刚刚讲过的这道题目动态规划:1143.最长公共子序列 (opens new window)就是一样一样的了。
一样到什么程度呢? 把字符串名字改一下,其他代码都不用改,直接copy过来就行了。
其实本题就是求最长公共子序列的长度,介于我们刚刚讲过动态规划:1143.最长公共子序列 (opens new window),所以本题我就不再做动规五部曲分析了。
如果大家有点遗忘了最长公共子序列,就再看一下这篇:动态规划:1143.最长公共子序列(opens new window)
本题代码如下:
class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length+1][nums2.length+1];/**本题其实核心含义就是找相同的子序列*/for (int i = 1; i <= nums1.length; i++) {for (int j = 1; j <= nums2.length; j++) {if (nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1]+1;}else {dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}return dp[nums1.length][nums2.length];}
}- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
53. 最大子序和
思路
这道题之前我们在讲解贪心专题的时候用贪心算法解决过一次,贪心算法:最大子序和 (opens new window)。
这次我们用动态规划的思路再来分析一次。
动规五部曲如下:
- 确定dp数组(dp table)以及下标的含义
dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]。
- 确定递推公式
dp[i]只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
- dp数组如何初始化
从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态,dp[0]就是递推公式的基础。
dp[0]应该是多少呢?
根据dp[i]的定义,很明显dp[0]应为nums[0]即dp[0] = nums[0]。
- 确定遍历顺序
递推公式中dp[i]依赖于dp[i - 1]的状态,需要从前向后遍历。
- 举例推导dp数组
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
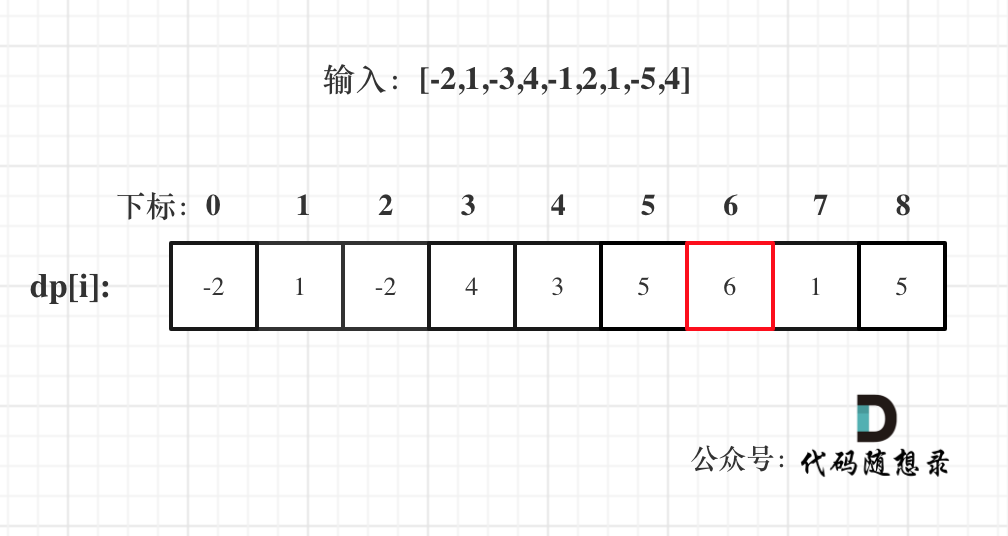
注意最后的结果可不是dp[nums.size() - 1]! ,而是dp[6]。
在回顾一下dp[i]的定义:包括下标i之前的最大连续子序列和为dp[i]。
那么我们要找最大的连续子序列,就应该找每一个i为终点的连续最大子序列。
所以在递推公式的时候,可以直接选出最大的dp[i]。
以上动规五部曲分析完毕,完整代码如下:
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int result = dp[0];for (int i = 1; i < nums.length; i++) {dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);// 状态转移公式result = Math.max(result,dp[i]);// result 保存dp[i]的最大值}return result;}
}- 时间复杂度:O(n)
- 空间复杂度:O(n)
相关文章:

代码随想录算法训练营第五十三天丨 动态规划part14
1143.最长公共子序列 思路 本题和动态规划:718. 最长重复子数组 (opens new window)区别在于这里不要求是连续的了,但要有相对顺序,即:"ace" 是 "abcde" 的子序列,但 "aec" 不是 &quo…...
pdf增强插件 Enfocus PitStop Pro 2022 mac中文版功能介绍
Enfocus PitStop Pro mac是一款 Acrobat 插件,主要用于 PDF 预检和编辑。这个软件可以帮助用户检查和修复 PDF 文件中的错误,例如字体问题、颜色设置、图像分辨率等。同时,Enfocus PitStop Pro 还提供了丰富的编辑工具,可以让用户…...
uniapp app tabbar 页面默认隐藏
1.在page.json 中找到tabbar visible 默认为true,设为false则是不显示 uni.setTabBarItem({ index: 1, //列表索引 visible:true //显示或隐藏 })...

深度学习 YOLO 实现车牌识别算法 计算机竞赛
文章目录 0 前言1 课题介绍2 算法简介2.1网络架构 3 数据准备4 模型训练5 实现效果5.1 图片识别效果5.2视频识别效果 6 部分关键代码7 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于yolov5的深度学习车牌识别系统实现 该项目较…...
:IM安全相关文章(Part12) [共15篇])
即时通讯技术文集(第23期):IM安全相关文章(Part12) [共15篇]
为了更好地分类阅读 52im.net 总计1000多篇精编文章,我将在每周三推送新的一期技术文集,本次是第23 期。 [- 1 -] 理论联系实际:一套典型的IM通信协议设计详解(含安全层设计) [链接] http://www.52im.net/thread-283-…...

为什么UI自动化难做?—— 关于Selenium UI自动化的思考
在快速迭代的产品、团队中,UI自动化通常是一件看似美好,实际“鸡肋”(甚至绝大部分连鸡肋都算不上)的工具。原因不外乎以下几点: 1 效果有限 通常只是听说过,就想去搞UI自动化的团队,心里都认…...

Python小白之“没有名称为xlwings‘的模块”
题外话:学习和安装Python的第一个需求就是整理一个Excel,需要读取和写入Excel 背景:取到的模板代码,PyCharm本地运行报错:没有名称为xlwings的模块 解决办法:这类报模板找不到的错,即是模块缺…...

RK3588 学习教程1——获取linux sdk
上手rk3588前,需要先拥有一块开发板,这样可以少走很多弯路。个人推荐买一块itx3588j的板子。挺好用,接口丰富,可玩性高。 sdk可以直接在firefly官网下载,不用管什么版本,下载下来后直接更新即可࿰…...
保护您的Google账号安全:检查和加固措施
简介:随着我们在日常生活中越来越依赖于Google账号,我们的个人信息和敏感数据也变得越来越容易受到威胁。为了确保您的Google账号的安全性,本文将介绍一些简单但有效的方法,帮助您检查和加固您的Google账号。 --- 在数字时代&am…...

「Verilog学习笔记」优先编码器Ⅰ
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 分析 分析编码器的功能表: 当使能El1时,编码器工作:而当E10时,禁止编码器工作,此时不论8个输入端为何种状态&…...
服务端-客户端)
java实现TCP通信(socket)服务端-客户端
我在写的时候,我的需求就很简单,写一个服务端,去让别人进行请求,借鉴了很多聊天室什么的,越搞越复杂。 期间也使用到了 BufferedReader中readLine()方法,进行获取客户端传来的数据&…...
企业信息模糊搜索API的使用及应用场景
前言 随着企业数据的不断增加,如何高效地搜索和管理这些数据成为了企业管理者关注的重要问题。而企业信息模糊搜索API的出现,为企业提供了一种高效的解决方案。本文将介绍企业信息模糊搜索API的使用及应用场景。 一、什么是企业信息模糊搜索API&#x…...

.net6+aspose.words导出word并转pdf
本文使用net6框架,aspose.word破解激活并兼容net6,导出word模板并兼容识别html并给其设置字体,前端直接浏览器下载,后端保存文件并返回文件流,还有批量导出并压缩zip功能 1、安装Aspose.Words的nuget包选择21.8.0 版本…...

深度学习 植物识别算法系统 计算机竞赛
文章目录 0 前言2 相关技术2.1 VGG-Net模型2.2 VGG-Net在植物识别的优势(1) 卷积核,池化核大小固定(2) 特征提取更全面(3) 网络训练误差收敛速度较快 3 VGG-Net的搭建3.1 Tornado简介(1) 优势(2) 关键代码 4 Inception V3 神经网络4.1 网络结构 5 开始训练5.1 数据集…...

《深入浅出进阶篇》洛谷P4147 玉蟾宫——悬线法dp
上链接:P4147 玉蟾宫 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P4147 上题干: 有一个NxM的矩阵,每个格子里写着R或者F。R代表障碍格子,F代表无障碍格子请找出其中的一个子矩阵,…...

社区论坛小程序源码系统,功能齐全,页面简洁,前端+后端+完整部署教程
现如今,社区论坛已经成为人们交流思想,分享经验,获取信息的重要平台。近年来,小程序的出现更是改变了传统的网站建设方式,让用户体验更加便捷,高效。今天源码小编来和大家分享一款社区论坛小程序源码系统&a…...
)
大数据开发面试(一)
1、Kafka 和 Flume 的应用场景? Kafka 和 Flume 的应用场景如下: Kafka:定位消息队列,适用于多个生产者和消费者共享一个主题队列的场景。适用于需要高吞吐量、可扩展性和容错能力的场景。主要用于大数据处理、实时数据流分析和日…...
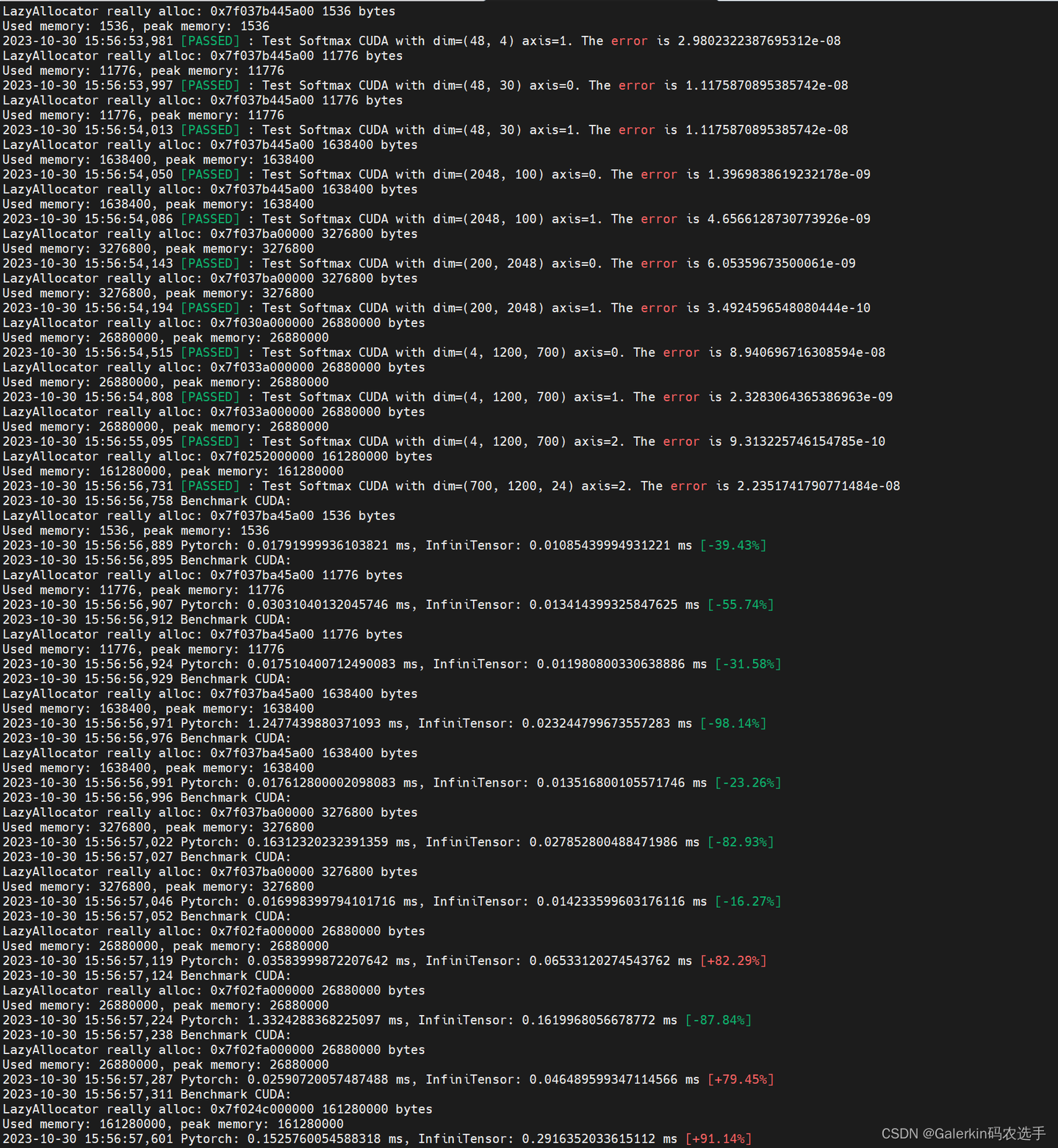
softmax的高效CUDA编程和oneflow实现初步解析
本文参考了添加链接描述,其中oneflow实现softmax的CUDA编程源代码参考链接添加链接描述 关于softmax的解读以及CUDA代码实现可以参考本人之前编写的几篇文章添加链接描述,添加链接描述,添加链接描述 下面这个图片是之前本人实现的softmax.cu经过接入python接口,最终和pytor…...

如何解决 Node.js 20 升级中未预期的请求问题
在 Tubi,我们使用 Node.js 为 Web/OTT 应用进行服务端渲染及代理请求。近来,为了从新版本的性能改进和新功能中受益,我们将 Node.js 从 14.x 版本升级到了 20.x。 升级像 Node.js 这样的基础设施绝非易事,尤其是有着许多第三方依…...

no tests were found
将带有Test的方法返回类型设为void...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
