《深入浅出进阶篇》洛谷P4147 玉蟾宫——悬线法dp
上链接:P4147 玉蟾宫 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P4147
https://www.luogu.com.cn/problem/P4147
上题干:
有一个NxM的矩阵,每个格子里写着R或者F。R代表障碍格子,F代表无障碍格子请找出其中的一个子矩阵,其元素均为‘F’,并且面积最大,输出它的面积*3的值
求最大子矩阵我们一般用到一个方法叫——悬线法;
下面来介绍悬线法:
我们找任意找一个非障碍格子作为底边的一个格子,从该点出发,引出3条直线,左直线,右直线,上直线。
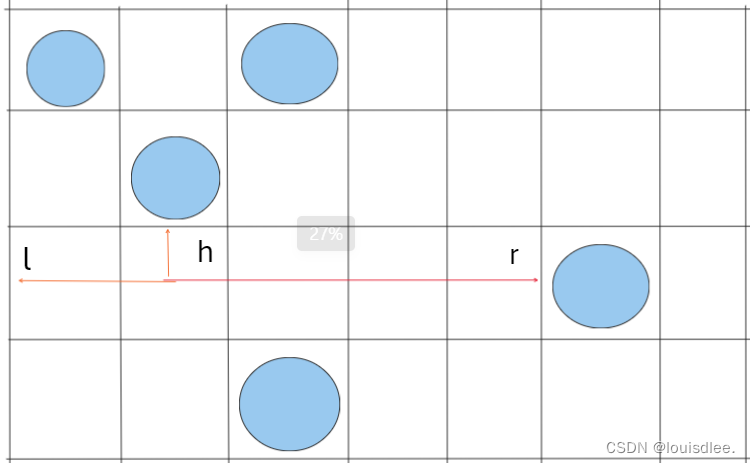
我们从这个点出发,向左一直延伸直到遇到障碍格,向右一直延伸一直延长到障碍格子,同理,向上也是。
第一步:
设置四个数组:
棋盘:char a[N][N];
左悬线数组:表示每个格子能向左延伸到的最远距离, int l[N][N];
右悬线 :表示每个格子能向右延伸到的最远距离,int r[N][N] ;
上悬线:表示每个格子能向上延伸到的最远距离 int h[N][N];
第二步:
求左悬线:
思路:
我们先将每个格子的向左能延伸到的最远距离初始化为该格子本身的列数,也就是它一开始只能延伸到它本身。
以第一行为例:

然后循环每一列,从最左边开始,当a[i][j]为空地,并且a[i][j-1]为空地的时候,该格子的左悬线能延伸到的位置就是左边一格能延伸到的位置。
所以有此代码:
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i][j - 1] == 'F')l[i][j] = l[i][j - 1];
这样就可以求出所有格子的左悬线了。
同理
求右悬线:
思路:
我们先将每个格子的向右能延伸到的最远距离初始化为该格子本身的列数,也就是它一开始只能延伸到它本身
循环每一列,从最右边开始,当a[i][j]为空地,并且a[i][j+1]为空地的时候,该格子的右悬线能延伸到的位置就是右边一格能延伸到的位置。
for (int i = 1; i <= n; i++)for (int j = m; j >= 1; j--)if (a[i][j] == 'F' and a[i][j + 1] == 'F')r[i][j] = r[i][j + 1];求上悬线:
思路:
我们先将每个格子的向上能延伸到的最远距离初始化为该格子本身的高度,即为1,也就是它一开始只能延伸到它本身
循环每一列,从任意一遍开始都行,我们以从左边开始为例子,当a[i][j]为空地,并且a[i-1][j]为空地的时候,该格子的上悬线能延伸到的位置就是上边一格能延伸到的位置。
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i - 1][j] == 'F')h[i][j] = h[i - 1][j] + 1;将这三个代码整合起来就是这样的:
for (int i = 1; i <= n; i++)
{for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i][j - 1] == 'F')l[i][j] = l[i][j - 1];for (int j = m; j >= 1; j--)if (a[i][j] == 'F' and a[i][j + 1] == 'F')r[i][j] = r[i][j + 1];for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i - 1][j] == 'F')h[i][j] = h[i - 1][j] + 1;
}第三步:
求每个格子以上悬线为高的矩形面积
到这里还没有结束,不要傻乎乎的就用每一个格子的三个悬线开始计算面积了。
我们应该可以注意到,有这样一种情况:

如果直接拿右悬线-左悬线 乘以高的话,求出来的面积 是绿色矩形的面积,然而实际上我们希望求的是在上悬线尽可能高的情况下的矩形面积(目的是使得枚举不重不漏)。
所以我们还需要修改一个条件,该格的左悬线应该为 (该格,和上面一格)的左悬线之间长度小的那一根。
由于l[i][j]代表的是该格向左能延伸到的最远的坐标(离得越远,坐标越小),所以我们需要让l[i][j]尽可能大,
同理,我们要让r[i][j]尽可能的小。
那么则有:
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++) if (a[i][j] == 'F' and a[i - 1][j] == 'F') {r[i][j] = min(r[i][j], r[i - 1][j]);l[i][j] = max(l[i][j], l[i - 1][j]);}到这里就基本结束了。
第四步:
最后我们只需要打擂台,不断求出每个格子三悬线组成的面积的最大值就可以了。
也就是:
for (int i = 1; i <= n; i++) if (a[i][j] == 'F')ans = max(ans, h[i][j] * (r[i][j] - l[i][j] + 1));
总的来看,这道题一共有四个步骤,设三条悬线,求三条悬线,求以上悬线为高的矩形面积,打擂台求最大值。
上代码:
const int N = 1010;
int n, m, ans;
char a[N][N];
int h[N][N], l[N][N], r[N][N];
int main()
{ans = 0;cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++){cin >> a[i][j];h[i][j] = 1, r[i][j] = l[i][j] = j;//初始化h,r,l}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i][j - 1] == 'F')l[i][j] = l[i][j - 1];for (int j = m; j >= 1; j--)if (a[i][j] == 'F' and a[i][j + 1] == 'F')r[i][j] = r[i][j + 1];for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i - 1][j] == 'F')h[i][j] = h[i - 1][j] + 1;}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++) {if (a[i][j] == 'F' and a[i - 1][j] == 'F') {r[i][j] = min(r[i][j], r[i - 1][j]);l[i][j] = max(l[i][j], l[i - 1][j]);}if (a[i][j] == 'F')ans = max(ans, h[i][j] * (r[i][j] - l[i][j] + 1));}}cout << 3 * ans;}相关文章:

《深入浅出进阶篇》洛谷P4147 玉蟾宫——悬线法dp
上链接:P4147 玉蟾宫 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P4147 上题干: 有一个NxM的矩阵,每个格子里写着R或者F。R代表障碍格子,F代表无障碍格子请找出其中的一个子矩阵,…...

社区论坛小程序源码系统,功能齐全,页面简洁,前端+后端+完整部署教程
现如今,社区论坛已经成为人们交流思想,分享经验,获取信息的重要平台。近年来,小程序的出现更是改变了传统的网站建设方式,让用户体验更加便捷,高效。今天源码小编来和大家分享一款社区论坛小程序源码系统&a…...
)
大数据开发面试(一)
1、Kafka 和 Flume 的应用场景? Kafka 和 Flume 的应用场景如下: Kafka:定位消息队列,适用于多个生产者和消费者共享一个主题队列的场景。适用于需要高吞吐量、可扩展性和容错能力的场景。主要用于大数据处理、实时数据流分析和日…...
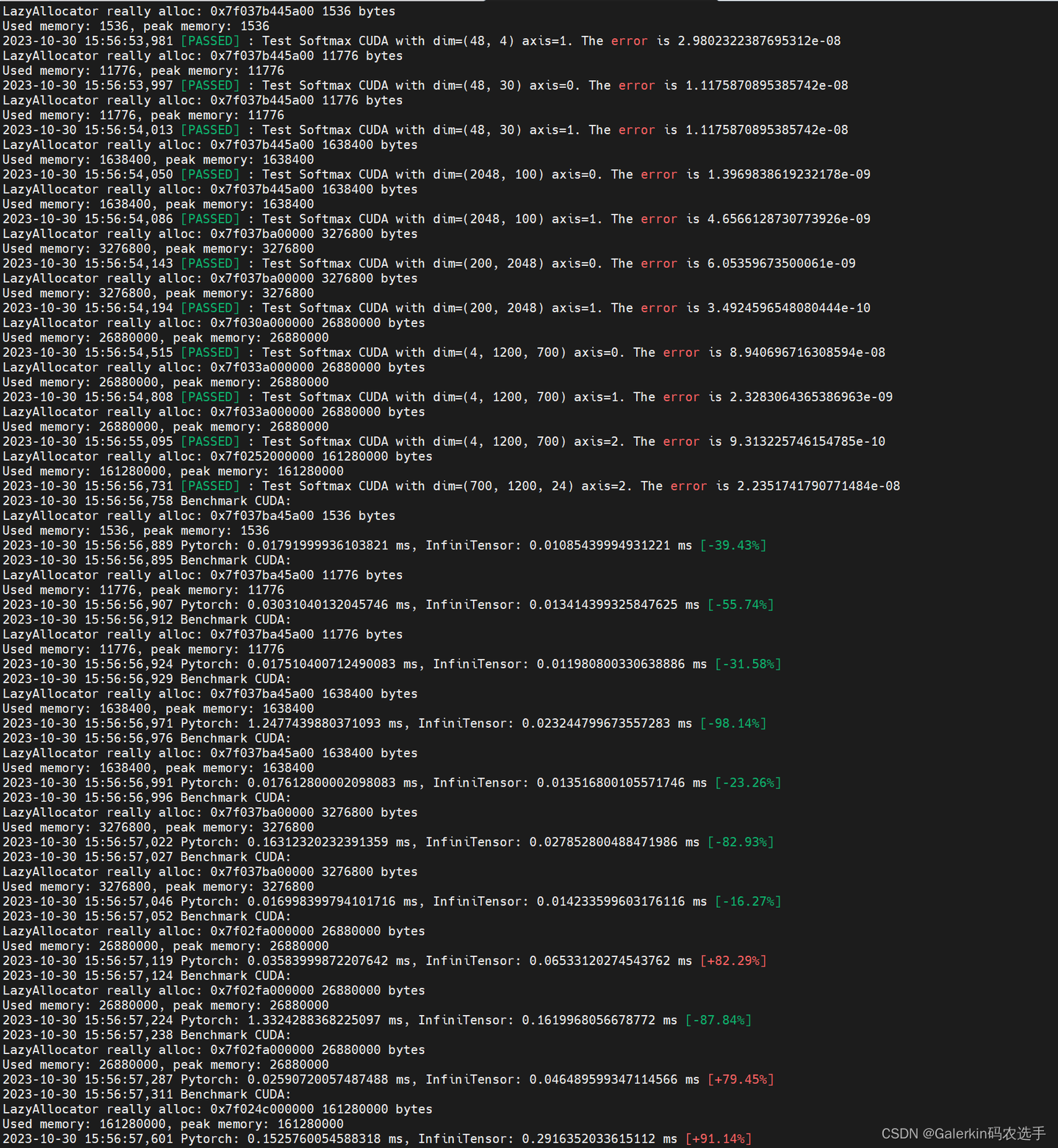
softmax的高效CUDA编程和oneflow实现初步解析
本文参考了添加链接描述,其中oneflow实现softmax的CUDA编程源代码参考链接添加链接描述 关于softmax的解读以及CUDA代码实现可以参考本人之前编写的几篇文章添加链接描述,添加链接描述,添加链接描述 下面这个图片是之前本人实现的softmax.cu经过接入python接口,最终和pytor…...

如何解决 Node.js 20 升级中未预期的请求问题
在 Tubi,我们使用 Node.js 为 Web/OTT 应用进行服务端渲染及代理请求。近来,为了从新版本的性能改进和新功能中受益,我们将 Node.js 从 14.x 版本升级到了 20.x。 升级像 Node.js 这样的基础设施绝非易事,尤其是有着许多第三方依…...

no tests were found
将带有Test的方法返回类型设为void...

泛型擦除是什么
//在编译阶段使用泛型,运行阶段取消泛型,就是擦除. //因为泛型其实只是在编译器中实现的而虚拟机并不认识泛型类项,所以要在虚拟机中将泛型类型进行擦除, //擦除是将泛型以其父类代替,如String变成了object等. //在使用的时候还是进行带强制类型转化,只不过这是比较安全的转换,…...

7、线性数据结构-切片
切片slice 容器容量可变,所以长度不能定死长度可变,元素个数可变底层必须依赖数组,可以理解它依赖于顺序表,表现也像个可变容量和长度顺序表引用类型,和值类型有区别 定义切片 var s1 []int //长度、容量为0的切片&…...
linux grub2 不引导修复 grub2-install:error:/usr/lib/grub/x86_64-efi/modinfo.sh
系统部署在物理机上,开机后一直pxe不进系统,怀疑GRUB丢失。 查看bios 里 采用uefi 启动方式, 无硬盘系统引导选项, 且BMC设置为硬盘永久启动也无效。 挂载光驱ISO进入救援模式,sda为系统盘,重装grub报错 grub2-inst…...

建筑楼宇智慧能源管理系统,轻松解决能源管理问题
随着科技的进步与人们节能减排意识的不断增强,建筑楼宇是当下节能减排的重要工具。通过能源管理平台解决能效管理、降低用能成本、一体化管控、精细化管理和服务提供有力支撑。 建筑楼宇智慧能源管理系统是一种利用先进手段,采用微服务架构,…...

【洛谷算法题】P5711-闰年判断【入门2分支结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5711-闰年判断【入门2分支结构】🌏题目描述🌏输入格式&a…...
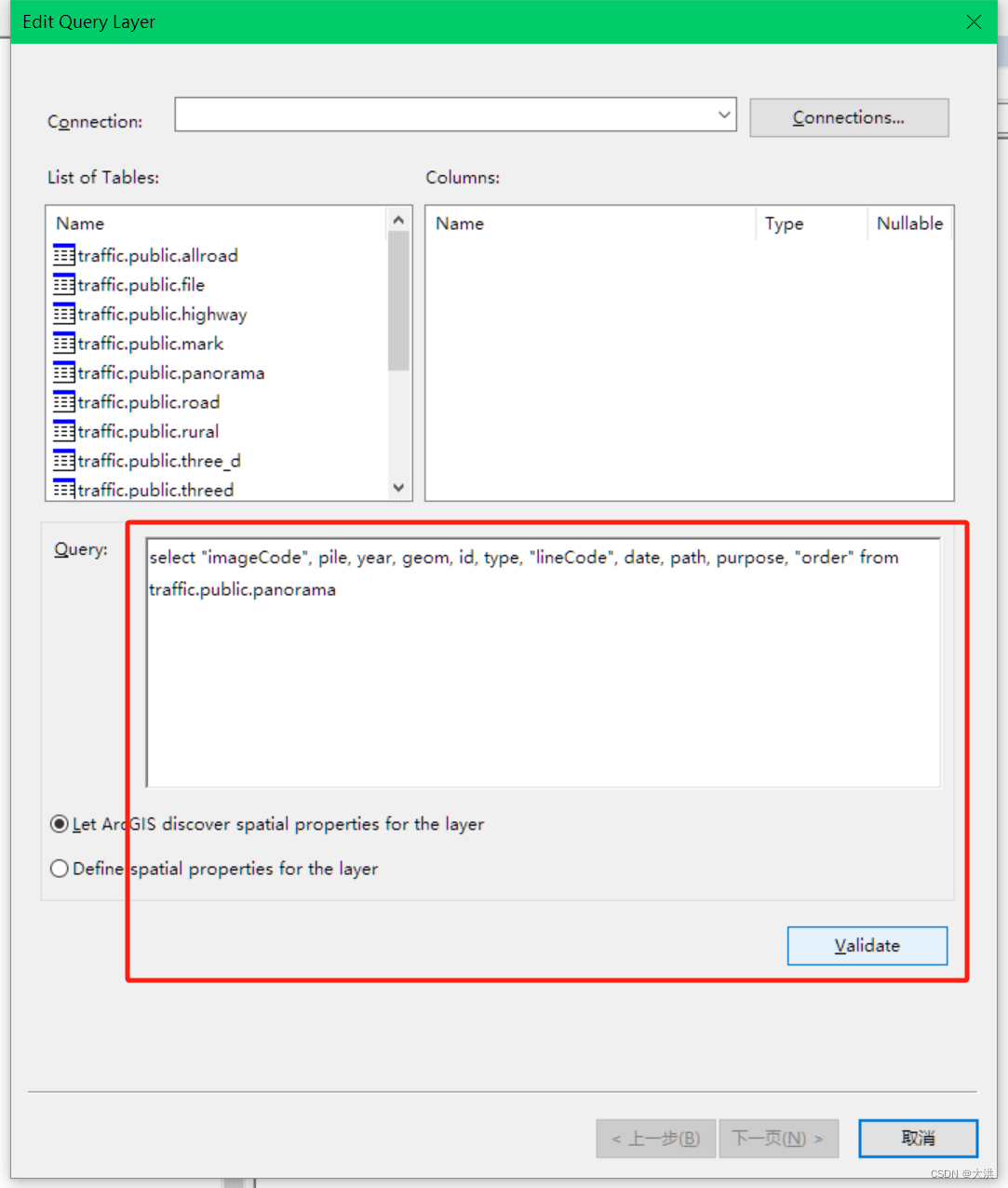
ArcGIS10.8 连接 PostgreSQL 及遇到的两个问题
前提 以前同事用过我的电脑连PostgreSQL,失败了。当时不知道原因,只能使用GeoServer来发布数据了。现在终于搞明白了,原因是ArcGIS10.2版本太老,无法连接PostgreSQL9.4。参考这里 为了适应时代的发展,那我就用新的Ar…...
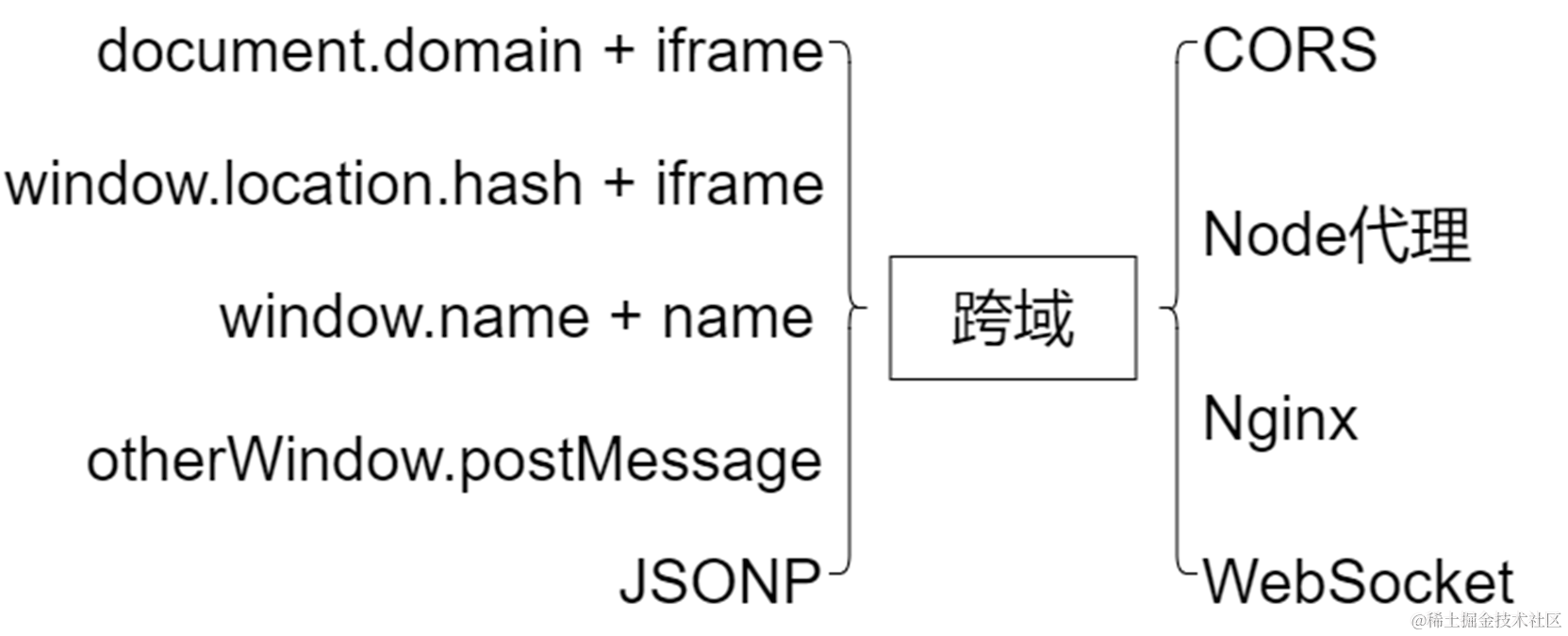
深入跨域 - 从初识到入门 | 京东物流技术团队
前言 跨域这两个字就像一块狗皮膏药一样黏在每一个前端开发者身上,无论你在工作上或者面试中无可避免会遇到这个问题。如果在网上搜索跨域问题,会出现许许多多方案,这些方案有好有坏,但是对于阐述跨域的原理和在什么情况下需要用…...
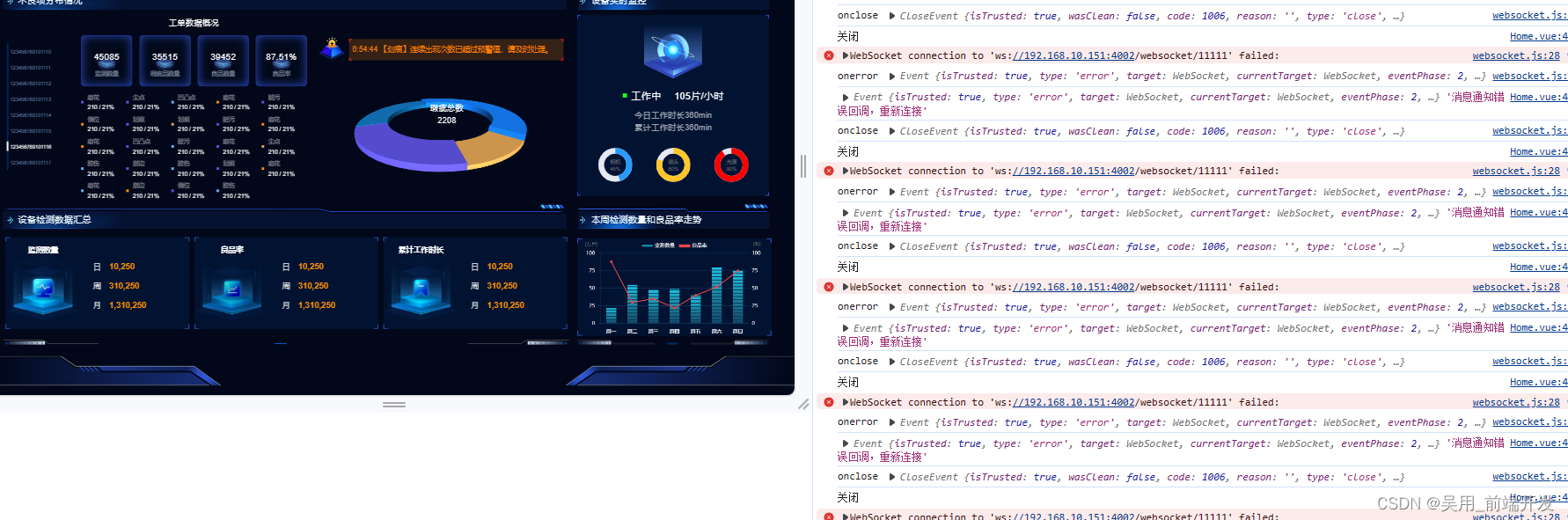
WebSocket真实项目总结
websocket websocket是什么? websocket是一种网络通讯协议。 websocket 是HTML5开始提供的一种在单个TCP链接上进行全双工通讯的协议。 为什么需要websocket? 初次接触websocket,都会带着疑惑去学习,既然已经有了HTTP协议,为什么还需要另一…...

Python 如何实现解释器(Interpreter)设计模式?什么是解释器设计模式?
什么是解释器(Interpreter)设计模式? 解释器(Interpreter)设计模式是一种行为型设计模式,它定义了一种语言文法的表示,并提供了一个解释器,用于解释语言中的句子。该模式使得可以定…...
单片机与PLC的区别有哪些?
单片机与PLC的区别有哪些? 什么是单片机? 单片机(Microcontroller,缩写MCU)是一种集成了中央处理器(CPU)、存储器和输入/输出接口等功能模块的微型计算机系统。它通常被用于嵌入式系统和控制系统中&#x…...

修改浏览器滚动条样式--ios同款
::-webkit-scrollbar{width: 5px;height: 5px; } ::-webkit-scrollbar-thumb{border-radius: 1em;background-color: rgba(50,50,50,.3); } ::-webkit-scrollbar-track{border-radius: 1em;background-color: rgba(50,50,50,.1); } 修改滚动条样式用到的CSS伪类: :…...
python自动化测试selenium核心技术3种等待方式详解
这篇文章主要为大家介绍了python自动化测试selenium的核心技术三种等待方式示例详解,有需要的朋友可以借鉴参考下,希望能够有所帮助,祝大家多多进步早日升职加薪 UI自动化测试过程中,可能会出现因测试环境不稳定、网络慢等情况&a…...
苹果手机照片如何导入电脑?无损快速的传输办法分享!
前些天小编的朋友联系到我,说是自己苹果手机里面的照片太多,有好几千张,不知道该怎么快而无损地传到电脑。我想遇到这种情况的不止是小编的朋友,生活中遇到手机照片导入电脑的同学不在少数。不管是苹果手机还是安卓手机࿰…...

csh 脚本批量处理文件并将文件扔给程序
文章目录 前言程序批量造 case 并将 cmd 扔给程序运行批量收集数据汇总 前言 Linux下我们经常会写一些shell脚本来辅助我们学习或者工作,从而提高效率。 之前就写过一篇博客:Linux下利用shell脚本批量产生内容有规律变化的文件 程序 批量造 case 并将…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
