Linux内核分析(十四)--内存管理之malloc、free 实现原理
目录
一、引言
二、malloc实现方式
------>2.1、动态内存分配的系统调用：brk / sbrk
------>2.2、malloc实现思路
------------>2.2.1、最佳适应法
------------>2.2.2、最差适应法
------------>2.2.3、首次适应法
------------>2.2.4、下一个适应法
------------>2.2.5、free
------>2.3、实现方式一：显式空闲链表 + 整块分配
------>2.4、显式空闲链表 + 按需分配
------>2.5、分离的空闲链表
------>2.6、分离适配
------>2.7、buddy系统的malloc
------>2.8、tcmalloc
------>2.9、总结
三、页面回收
------>3.
相关文章：
--内存管理之malloc、free 实现原理)
Linux内核分析(十四)--内存管理之malloc、free 实现原理
目录 一、引言 二、malloc实现方式 ------>2.1、动态内存分配的系统调用：brk / sbrk ------>2.2、malloc实现思路 ------------>2.2.1、最佳适应法 ------------>2.2.2、最差适应法 ------------>2.2.3、首次适应法 ------------>2.2.4、下一个适应…...
Hive函数
1. Hive 内置运算符 整体上，Hive 支持的运算符可以分为三大类：关系运算、算术运算、逻辑运算。 官方参考文档：LanguageManual UDF - Apache Hive - Apache Software Foundation 也可以使用下述方式查看运算符的使用方式： -- 显…...
教资笔记（目录）
目录 中小学教资笔记总结中学教资小学教资小学中学科一《综合素质》（通用）：考情分析：学习笔记 小学科二《教育知识与能力》：考情分析：学习笔记： 中小学教资笔记总结 2023.9.16教资考试 笔试成绩…...
的注意事项)
np.repeat()的注意事项
对于一个shape为（3, 2）的矩阵a， b a.repeat(9, axis1)。 那b[:, :9]是相同的，b[:, 9:]是相同的，意见 a np.random.rand(3, 2) b a.repeat(9, axis1) np.all(b[:, 0] b[:, 1]), np.all(b[:, 0] b[:, 9]) Out: (Tr…...
239. 滑动窗口最大值
239. 滑动窗口最大值 原题链接：完成情况：解题思路：参考代码：错误经验吸取 原题链接： 239. 滑动窗口最大值 https://leetcode.cn/problems/sliding-window-maximum/description/ 完成情况： 解题思路&…...
c++ barrier 使用详解
c barrier 使用详解 std::barrier c20 头文件 #include <barrier>。作用：一般被用来协调多个线程，在所有线程都到达屏障点之后，才允许它们继续执行，对于需要线程间同步的并行算法和任务来说非常有用。使用步骤：…...
c# 接口
c#接口 namespace demo1 {/// <summary>/// 接口使用interface关键字进行定义/// 接口中只能声明方法不能定义，也就是说声明的方法不能有方法体。/// 接口不能包含常量、字段、运算符、实例构造函数、析构函数或类型，不能包含静态成员。由于不能有…...
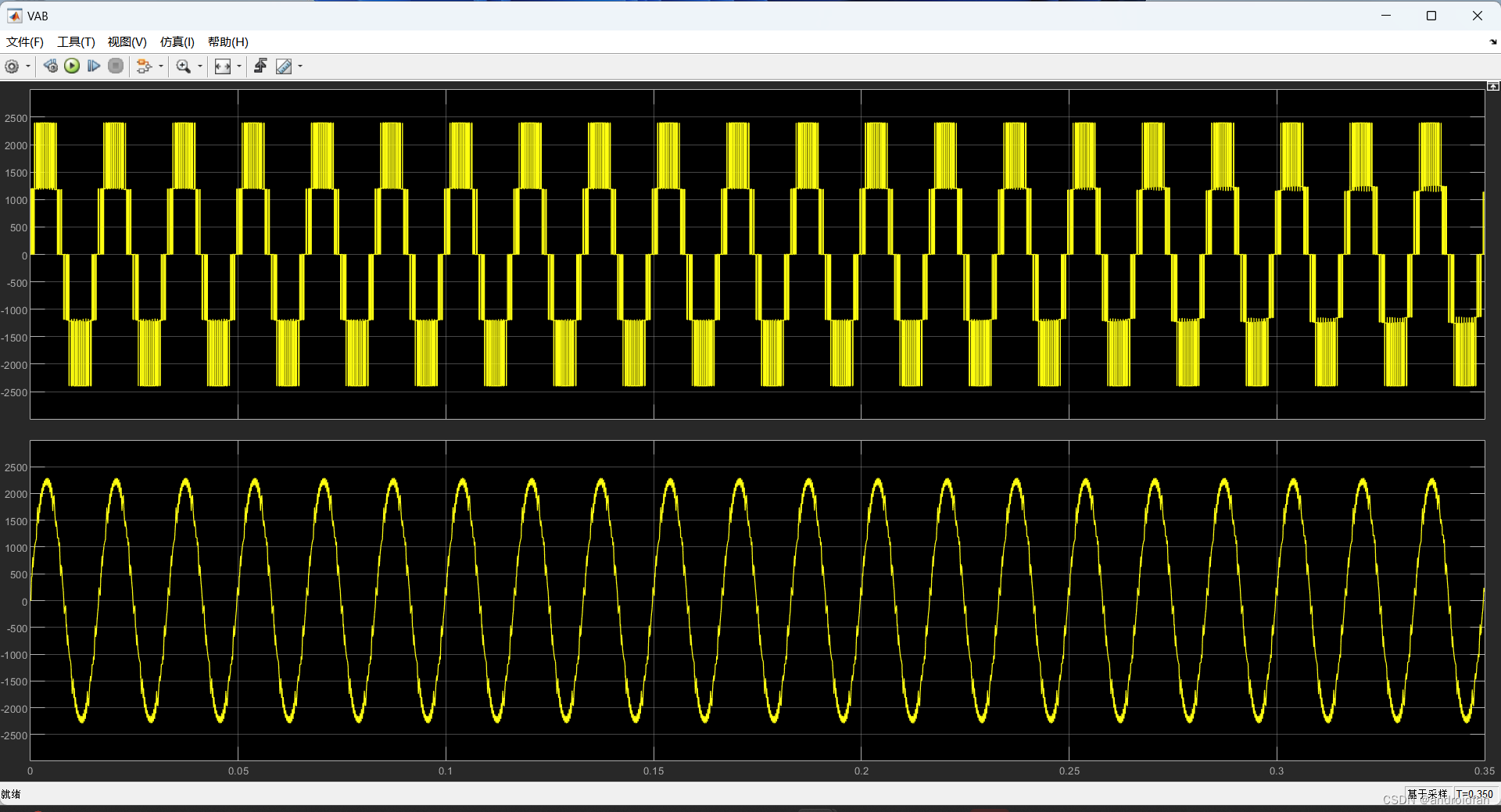
1、NPC 三电平SVPWM simulink仿真
1、SVPWM时间计算函数，是从matlab的SVPWM3L_TimingCalculation.p文件中反汇编出来的函数： function [TgABC_On ,TgABC_Off ,Sn ]SVPWM3L_TimingCalculation_frompfile (Vref ,DeltaVdc ,Fsw ) %#codegen %coder .allowpcode (plain ); TgABC_On [0 ,0 ,…...
JAVA对象列表强转失败，更好的方法
JAVA将无法强转的list泛型对象使用JSON工具类转换为list类 List<DiskUseRateVo> list JSON.parseArray(JSON.toJSONString(httpGet(url).getContent()), DiskUseRateVo.class);之前一直强转发现后续list.get(0)报错，用JSON解决了问题。...
2023最新版本 从零基础入门C++与QT（学习笔记） -5- 动态内存分配(new)
🎏C的动态内存要比C方便 🎄注意C申请内存的时候可以直接的初始化！！！ 🎄格式（申请一块内存） 🎈new(关键字) 变量类型 🎄格式（申请多块内存&am…...
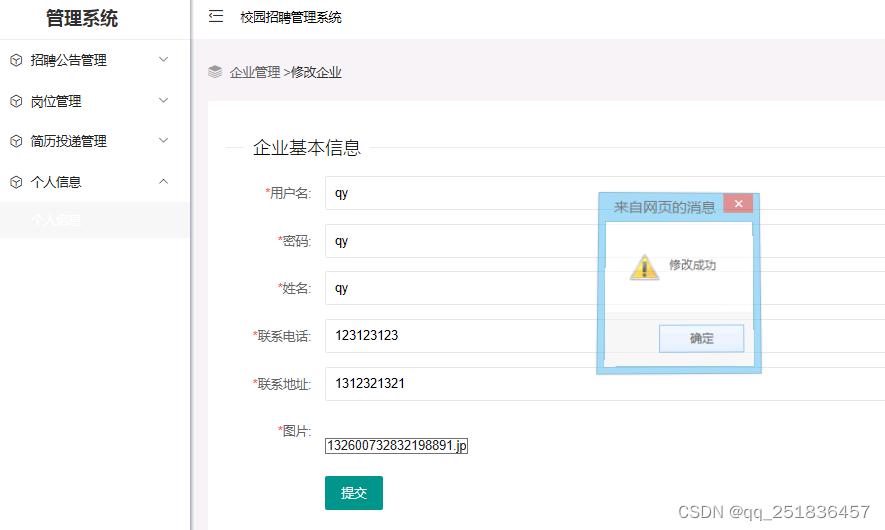
asp.net校园招聘管理系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net 校园招聘管理系统是一套完善的web设计管理系统，系统具有完整的源代码和数据库，系统主要采用B/S模式开发。开发环境为vs2010，数据库为sqlserver2008，使用c#语言开发 应用技术：asp.net c#s…...
flink的键值分区状态自动过期ttl配置
背景 flink的状态清理之前一直都是通过处理函数的ontimer设置定时器的方式清理掉那些无用的状态，但是这种方式容易出错而且代码也不优雅，使用flink提供的状态ttl的方式可以解决这个问题 flink键值分区状态ttl设置 文件系统/基于内存的状态后端的ttl设…...
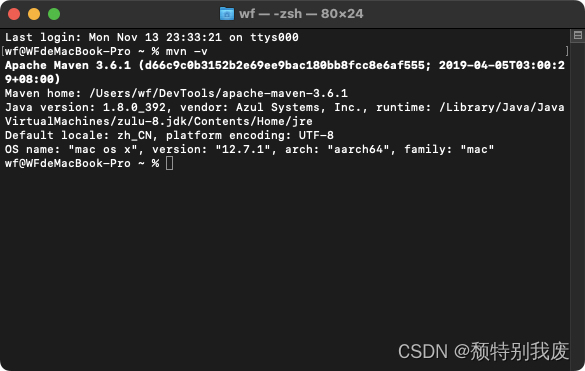
解决Mac配置maven环境后，关闭终端后环境失效的问题(适用于所有终端关闭后环境失效的问题)
目录 问题的原因 解决方式一、每次打开终端时输入："source ~/.bash_profile"，这个方式比较繁琐 解决方式二、我们终端输入"vim ~/.zshrc"打开".zshrc"文件 1、我们输入以下代码： 2、首先需要按 " i…...
springboot运行jar包，实现复制jar包resources下文件、文件夹（可支持包含子文件夹）到指定的目录
背景： 以jar包运行时，获取文件目录时，会报错； idea运行不会报错。 代码： //复制文件夹到指定路径下 String srcFilePath Thread.currentThread().getContextClassLoader().getResource("").getPath() &…...
Webpack Bundle Analyzer包分析器
当我们需要分析打包文件dist里哪些资源可以进一步优化时，就可以使用包分析器插件webpack-bundle-analyzer。NPM上的介绍是使用交互式可缩放树图可视化 webpack 输出文件的大小。 我的是vue2项目。 1、webpack-bundle-analyzer插件的安装 $ npm install --save-dev…...
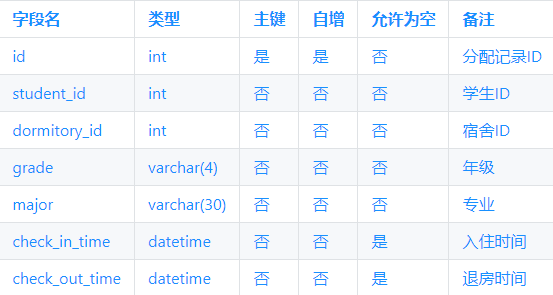
SQL-----STUDENT
【学生信息表】 【宿舍信息表】 【宿舍分配表】 为了相互关联，我们需要在表中添加外键。在宿舍分配表中添加用于关联学生信息表的外键 student_id，以及用于关联宿舍信息表的外键 dormitory_id； sql代码 -- 创建学生信息表 CREATE TABLE st…...
OpenCV入门——图像视频的加载与展示一些API
文章目录 OpenCV创建显示窗口OpenCV加载显示图片OpenCV保存文件利用OpenCV从摄像头采集视频从多媒体文件中读取视频帧将视频数据录制成多媒体文件OpenCV控制鼠标关于[np.uint8](https://stackoverflow.com/questions/68387192/what-is-np-uint8) OpenCV中的TrackBar控件TrackBa…...
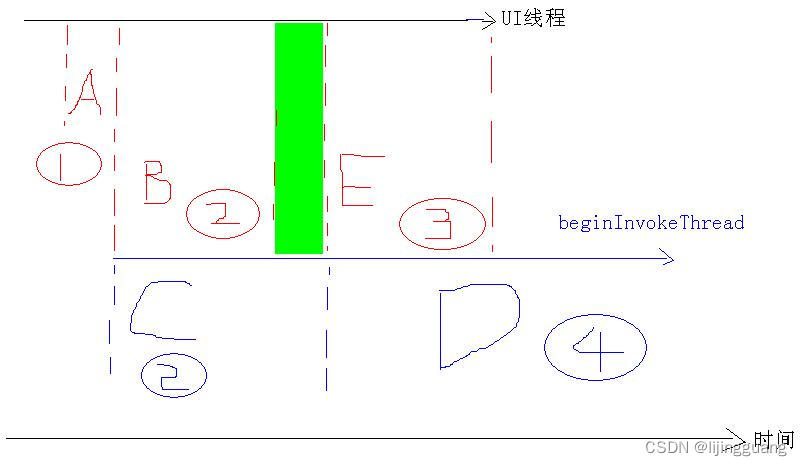
Control的Invoke和BeginInvoke
近日，被Control的Invoke和BeginInvoke搞的头大，就查了些相关的资料，整理如下。感谢这篇文章对我的理解Invoke和BeginInvoke的真正含义 。 (一）Control的Invoke和BeginInvoke 我们要基于以下认识： （1&#x…...
什么是OpenCL？
什么是OpenCL？ 1.概述 OpenCL(Open Computing Language 开放计算语言)是一种开放的、免版税的标准，用于超级计算机、云服务器、个人计算机、移动设备和嵌入式平台中各种加速器的跨平台并行编程。OpenCL是由Khronos Group创建和管理的。OpenCL使应用程序…...
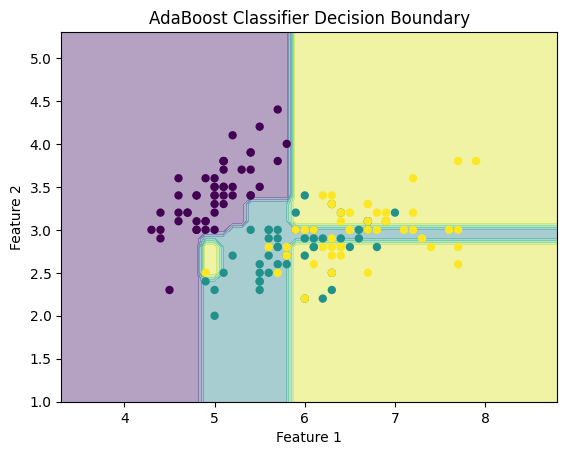
AdaBoost：提升机器学习的力量
一、介绍 机器学习已成为现代技术的基石，为从推荐系统到自动驾驶汽车的一切提供动力。在众多机器学习算法中，AdaBoost（Adaptive Boosting的缩写）作为一种强大的集成方法脱颖而出，为该领域的成功做出了重大贡献。AdaBoo…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课，做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程，它的核心机制是 Goroutine 协程、Channel 通道，并基于CSP（Communicating Sequential Processes࿰…...
Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案，允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性：使神经网络可学习复杂模式控制输出范围：如Sigmoid将输出限制在(0,1)梯度传递：影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
select、poll、epoll 与 Reactor 模式
在高并发网络编程领域，高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表，以及基于它们实现的 Reactor 模式，为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
Map相关知识
数据结构 二叉树 二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子 节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只 有左子节点，有的节点只有…...
深度学习习题2
1.如果增加神经网络的宽度，精确度会增加到一个特定阈值后，便开始降低。造成这一现象的可能原因是什么？ A、即使增加卷积核的数量，只有少部分的核会被用作预测 B、当卷积核数量增加时，神经网络的预测能力会降低 C、当卷…...
基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发，数据库mysql，前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式，给定一个隐函数关系： F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标： 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...