2020年五一杯数学建模C题饲料混合加工问题解题全过程文档及程序
2020年五一杯数学建模
C题 饲料混合加工问题
原题再现
饲料加工厂需要加工一批动物能量饲料。饲料加工需要原料,如加工猪饲料需要玉米、荞麦、稻谷等。加工厂从不同的产区收购了原料,原料在收购的过程中由于运输、保鲜以及产品本身属性等原因,存在着效能率的问题(如1吨玉米可加工成0.7吨左右的玉米面)。这个数据在原料进厂之后可以通过随机抽样进行检测得到。
某饲料加工厂有9个加工窖,现有一批加工任务,要将16个加工原料(见表1)按照某种混合方案一次性放入加工窖中进行加工。一个加工窖的混合产品称为一个加工包。如果某加工原料重量不少于500千克,则可以单独成为一个加工包。因产品属性原因,要求品种代码10的加工原料不能单独成为一个加工包。每一个加工窖能够加工的重量有限定范围(见表2)。加工窖加工成本由点火成本(也称固定成本)与加工量成本(也称可变成本)构成,其他成本暂不考虑。表1提供了各加工原料的品种代码、总重量和效能率。表2提供了每一个加工窖能够加工的重量范围以及点火成本、加工量单位成本数据。
由于加工窖数量低于饲料加工原料的品种数,所以在加工前需要将若干个加工原料进行混合。为了保证加工后饲料的质量,要求混合的任何两个加工原料之间必须具有亲缘关系。工厂技术人员对每种加工原料进行了基因检测,得到了10个关键位点的基因序列(见表1),并规定,两个加工原料如果有N个相同位点的基因序列标记相同,就认为这两个加工原料的亲缘值为N(如果N大于0,则说明这两种加工原料之间具有亲缘关系),一个加工包中所有原料两两之间亲缘值的平均值称为亲缘度。例如品种代码1、2、5的加工原料混合成为一个加工包,假设品种代码1和品种代码2的亲缘值为5,品种代码1和品种代码5的亲缘值为3,品种代码2和品种代码5的亲缘值为5,那么它们的亲缘度就是(5+3+5)/3。如果一个加工包中只含有一种加工原料,则该加工包的亲缘度为10。本题仅从亲缘度角度考虑混合加工饲料的质量,亲缘度越高,饲料质量就越高。
请考虑下列问题:
1. 请研究16个加工原料两两之间的亲缘值,并进行统计性分析。
2. 将16个加工原料进行混合全部放入9个加工窖中。请建立数学模型,求出饲料质量最高的混合方案并给出每个加工包的亲缘度。
3. 将16个加工原料进行混合全部放入9个加工窖中。请建立数学模型,求出平均能耗率超过80%的加工包数量最多的混合方案并给出每个加工包的能耗率,并将结果填入表3。
4. 如果饲料加工厂允许部分加工窖不生产,请建立数学模型,给出混合加工方案,用尽量低的加工成本完成整个加工任务,同时要求平均能耗率超过80%的加工包尽量的多。
5. 如果饲料加工厂允许部分加工窖不生产,但必须完成整个加工任务。请建立数学模型,给出混合加工方案使得(1)饲料质量尽量高,(2)加工成本尽量低,(3)平均能耗率超过80%的加工包尽量多。
整体求解过程概述(摘要)
近年来,养殖业迅猛发展,对于饲料的需求日益增加,导致饲料混合加工行业竞争十分激烈。因此,企业都在积极寻求质优价廉高效的饲料配比方案。本文通过数学模型,就饲料配比加工方案进行优化,给出最优的饲料混合配比方案。
针对问题一,对饲料两两加工原料之间的亲缘关系进行研究。饲料两两加工原料之间的亲缘关系用两种原料的对应 10 个关键点的基因序列相同个数进行判断,其表征为亲缘值大小。利用 Matlab 进行编程,获得两两加工原料的亲缘值表。对两两加工原料亲缘关系利用 IBM SPSS statistics 进行统计分析获得两两加工原料亲缘关系有 40 种,最大值为 6,最小值为 1,亲缘值范围长度为 5,亲缘值方差为 2.254,标准偏差为 1.50128,均值为 3.0500。
针对问题二,要求将 16 种加工原料全部放入 9 个加工窖中进行加工,求出能得出饲料质量最高的混合并给出每个加工包的亲缘度,实际上是一个优化问题。以加工原料的混合配比方案的亲缘度为优化目标。假设所有加工窖在加工过程中完全可以正常使用;只考虑亲缘度对混合加工饲料质量的影响;假设只考虑加工窖的点火成本和加工量成本,其他成本不考虑。建立亲缘度优化目标函数,给出配比方案的质量系数矩阵 A,在满足加工窖质量上下限约束和特定种类不能单独混合约束条件下,通过 Matlab 编程,结合蒙特卡洛算法进行优化,得到亲缘度最大的原料混合配比加工方案,亲缘度的最大值为 50.667。
针对问题三,要求将 16 个加工原料进行混合全部放入 9 个加工窖中,求出平均效能率超过 80%的加工包数量最多的混合方案并给出每个加工包的效能率,也是最优问题,优化目标函数为加工包的能耗率最大问题。影响单个加工包效能率的因素为每个加工窖中的每种加工原料的质量分配。在问题 2 的基础之上结合题目三所给的约束条件进行求解。利用蒙特卡洛算法进行优化,得到平均能耗效率超过 0.8 的加工包有 7 个 ,另外两个加工包的效率也在 0.7-0.8 之间。
针对问题四,从本质上来说,问题 4 属于双目标优化问题,问要求在允许部分加工窖不生产的情况下,满足成本尽量低,平均效能率超过 80%的加工包尽量多,取消一次性加工限制,可以多次加工。即在各种约束条件下设计出一个可以使得成本最小化、平均效能率超过 80%的加工包尽量多的混合方案。建立成本最低,加工包能耗率大于 0.8 数量尽可能多的目标函数,利用线性加权和法进行双目标优化,经过优化得线性加权和后的目标函数的最优解为 0.9548,其中成本为14350 元,效能值大于 0.8 的加工包的数量为 5。
问题五与问题四类似,属于多目标优化问题。经优化得线性加权后得目标函数得最优解为 0.9091,在此种配比情况下亲缘值为 43,即为质量最好,成本为14474 元,效能率大于 0.8 的加工包数量为 4。
模型假设:
[1]假设所有加工窖在加工过程中完全可以正常使用。
[2]假设只考虑亲缘度对混合加工饲料质量的影响。
[3]假设只考虑加工窖的点火成本和加工量成本,其他成本不考虑。
问题分析:
问题 1 的分析
问题 1 要求研究 16 个加工原料两两之间的亲缘值,并进行统计性分析。因此,首先根据题目所给亲缘值定义:即两个加工原料如果有 N 个相同位点的基因序列标记相同,就认为这两个加工原料的亲缘值为 N(如果 N 大于 0,则说明这两种加工原料之间具有亲缘关系)。由于是两两原料之间,且两元素之间不存在先后顺序问题,所以利用 matlab 进行编程,筛选出两两加工原料的组合方式,并计算出两两加工原料之间的亲缘值,然后利用 IBM SPSS Statistics 对数据进行统计分析。
问题 2 的分析
问题 2 要求将 16 种加工原料全部放入 9 个加工窖中进行加工,建立数学模型,求出能得出饲料质量最高的混合并给出每个加工包的亲缘度。显然问题二最终目标是求取亲缘度最优值问题,并给出饲料质量最高的混合方案(仅从亲缘度角度考虑混合加工饲料的质量,亲缘度越高,饲料质量就越高)。将 16 中种加工原料进行混合投放到 9 个加工窖中进行加工,由于每个加工窖中投放的加工原料组合不同以及每种组合方式的加工原料的重量分配比例也不确定,因此每个加工窖的加工原料组合具有随机性。因此我们将加工窖中加工原料混合方案问题看作是蒙特卡洛算法的优化组合方案问题。在考虑加工原料混合方案时,如何确定每一个加工窖的投放的加工原料的种类以及各种加工原料的重量占比是本问题的难点。但是,从企业的经营方式和经营目的来看生产方式必定是符合实际的,生产方案必定追求合理性,因此我们对于每个加工窖中的加工原料种类限制在 1 到 4 之间。原料种类大于 4 种的不予考虑,这就极大的简化了问题的复杂程度,并且该简化是合理的,符合企业实际生产的。同时要求混合方案达到质量最高的同时,还必须使投放的混合原料的重量在加工窖的加工重量范围上限和下限之间。我们从 9 个加工窖进行着手,通过建立加工原料重量组合系数矩阵,将每个加工窖的质量范围进行约束,从而建立数学模型,进行求解。
问题 3 的分析
问题 3 是将 16 个加工原料进行混合全部放入 9 个加工窖中,求出平均效能率超过 80%的加工包数量最多的混合方案并给出每个加工包的效能率。显然问题三同问题二一样属于最优问题,并在约束条件之下寻找加工原料的最优混合方案。问题中包含 16 种元素,9 个加工窖。假设在加工原料混合方案确定后,将混合原料投放到 9 个加工窖形成 9 个加工包。则每一个加工包都有一个效能率。通过对 16 种加工原料相关数据的分析,不难发现,由于加工窖自身没有加工效率问题,我们默认加工窖的加工效率是 1,对于每个加工包的效能率无影响。同时每种加工原料的能效率是定值,且不会随着外界条件发生改变。因此,影响单个加工包效能率的因素为每个加工窖中的每种加工原料的质量分配。在明确影响因素的前提条件下,建立起优化目标函数,在问题 2 的基础之上结合题目三所给的约束条件进行求解。利用蒙特卡洛算法进行优化,获得最优解,给出方案配比完成附表 3。
问题 4 的分析
问题 4 要求在允许部分加工窖不生产的情况下,满足给定的两个条件,一个是成本尽量低,另一个是平均效能率超过 80%的加工包尽量多,进而完成加工任务,即取消一次性加工的限制,可以多次加工。从本质上来说,问题 4 属于双目标优化问题,即在各种约束条件下设计出一个可以使得成本最小化、平均效能率超过 80%的加工包尽量多的混合方案。我们采用线性加权和法进行双目标优化。该问题的难点在于同时从成本以及效能率两个角度进行考虑,将复杂的任务预定规则转化为约束条件。在考虑加工成本最低时,我们发现加工窖的容量越大,加工成本越低,因此优先使用加工容量较大的加工窖进行加工。我们按照加工要求,设定约束条件,求解双目标优化模型。
问题 5 的分析
问题5的建模与求解过程是综合考虑前4个问题的求解结果进行优化计算的,问题 5 共有 3 个目标函数,属于多目标函数优化问题。由于这 3 个目标函数的最优解已经得到,因此我们直接采用线性加权和法进行求解,建立目标函数。假设饲料质量、加工成本和效能率对工厂加工的重要性相等,我们分别赋予每个指标各三分之一的权系数,以问题 2、问题 3 和问题 4 求解的最优值作为基准,建立新的目标函数进行优化。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
[num,jy,raw]=xlsread('temp.xlsx');
qyz=zeros(120,3);
count=0;
for i=1:15for m=i+1:16count=count+1;qyz(count,1)=num(i,1);qyz(count,2)=num(m,1);for j=1:10jdg=strcmp(jy(i,j),jy(m,j));if jdgqyz(count,3)=qyz(count,3)+1;endendend
end
temp=find(qyz(:,3));
yxqyz=qyz(temp,:);
qyzpj=mean(qyz(:,3));
stdqyz=std(qyz(:,3));
count=1;
num2=nan.*ones(16);
for i=1:size(qyz,1)num2(qyz(i,1),qyz(i,2))=qyz(i,3);num2(qyz(i,2),qyz(i,1))=qyz(i,3);num2(qyz(i,1),qyz(i,1))=10;
end
num2(16,16)=10;
for i=1:14for j=i+1:15for k=j+1:16if num2(i,j)*num2(i,k)*num2(j,k)~=0qy3z(count,1:3)=[i,j,k];qy3z(count,4)=(num2(i,j)+num2(i,k)+num2(j,k))/3;qy3z(count,5)=num(i,2)+num(j,2)+num(k,2);count=count+1;endendend
end
ttt=find(qy3z(:,5)>1200);
qy3z(ttt,:)=[];
function [ xxx ] = creatxbq()
%UNTITLED13 Summary of this function goes here
% Detailed explanation goes here
tryload qyzload luziload slzlalphab=1:16;syu=ones(1,16);xxx=zeros(9,16);qudiao=ceil(4*rand());qudiao=qudiao-1;if qudiaoprob=[100 100 100 20 20 20 1 1 1];prob=prob/sum(prob);luzinm=1:9;kd=[];while max(size(kd))~=qudiaokd1=randsrc(1,qudiao,[luzinm;prob]);kd = unique (kd1);endend for i=9:-1:1jdg=find(kd==i);if isempty(jdg)==0 &&i~=1jdg=[];continueend if isempty(jdg)==0 && i==1 else dq=ones(1,4); temp=1./(abs(syu-ones(1,16)*luzi(1,i))+0.1);prob=temp/sum(temp);if i==9||i==8||i==7 endnumi1=randsrc(1,1,[alphab;prob]);dq(1,1)=numi1;if syu(numi1)*slzl(numi1)<luzi(1,i)bl1=syu(numi1);elseif syu(numi1)*slzl(numi1)>=500 && numi1~=10bl1=500/slzl(numi1);elsebl1=luzi(1,i)/slzl(numi1);endendxxx(i,numi1)=bl1;mass=xxx(i,:)*slzl;syu(numi1)=syu(numi1)-xxx(i,numi1);if numi1==10||mass<500%xuan2elseif mass>=luzi(1,i) && i~=1continue endend mass=(xxx(i,:)*slzl);qyi1=find(qyz(dq(1,1),:));qyi1(find(qyi1==numi1))=[];if sum(syu(qyi1))~=0prob=syu(qyi1)/sum(syu(qyi1));numi2=randsrc(1,1,[qyi1;prob]);dq(1,2)=numi2;if mass+syu(numi2)*slzl(numi2)<=luzi(1,i)bl2=syu(numi2);elseslslsl=luzi(2,i)-(xxx(i,:)*slzl);slslmin=luzi(1,i)-xxx(i,:)*slzl;if slslmin<0slslmin=0;endbl2=ceil(100*(slslmin/slzl(numi2)+(50/slzl(numi2))*rand()))/100;endxxx(i,numi2)=bl2;mass=(xxx(i,:)*slzl);syu(numi2)=syu(numi2)-xxx(i,numi2);if mass>=luzi(1,i) && mass<=luzi(2,i)&&i~=1continueendqyi112=qyi1;
count=0;for j=1:size(qyi1,2)if qyz(qyi1(j),numi2)~=0count=count+1;qyi12(count)=qyi112(j);endendqyi12(find(qyi12==numi2))=[];if sum(sum(syu(qyi12)))~=0prob=syu(qyi12)/sum(syu(qyi12));numi3=randsrc(1,1,[qyi12;prob]);mass=(xxx(i,:)*slzl);if mass+syu(numi3)*slzl(numi3)<=luzi(2,i)bl2=syu(numi3);elseslslsl=luzi(2,i)-(xxx(i,:)*slzl);slslmin=luzi(1,i)-xxx(i,:)*slzl;if slslmin<0slslmin=0;endbl2=slslmin/slzl(numi3);endxxx(i,numi3)=bl2;syu(numi3)=syu(numi3)-xxx(i,numi3); endendmass=(xxx(i,:)*slzl);if mass<luzi(1,i)tttt=find(xxx(i,:));for j=1:max(size(find(xxx(i,:))))ysl=find(xxx(:,tttt(j)));for k=1:max(size(ysl))yslimass=(xxx(ysl(k),:)*slzl-luzi(1,ysl(k)))/slzl(j);if xxx(ysl(k),tttt(j))<yslimassxxx(i,tttt(j))=xxx(i,tttt(j))+
xxx(ysl(k),tttt(j))-1/slzl(j);xxx(ysl(k),tttt(j))=1/slzl(j);elsexxx(i,tttt(j))=xxx(i,tttt(j))+yslimass;
xxx(ysl(k),tttt(j))=
xxx(ysl(k),tttt(j))-yslimass;
endendend end end if i==1jsy=find(syu);if jsyfor j=1:max(size(jsy))yyy=find(xxx(:,jsy(j)));if yyyfor k=1:size(yyy)if syu(jsy(j))==0continueend
ksy=luzi(2,yyy(k))-xxx(yyy(k),:)*slzl;
if ksyif ksy>syu(jsy(j))*slzl(jsy(j))xxx(yyy(k),jsy(j))=xxx(yyy(k),jsy(j))+syu(jsy(j));syu(jsy(j))=0;elsexxx(yyy(k),jsy(j))=xxx(yyy(k),jsy(j))+ksy/slzl(jsy(j));syu(jsy(j))=syu(jsy(j))-ksy/slzl(jsy(j));end endend endendendend end
catch
end
end
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2020年五一杯数学建模C题饲料混合加工问题解题全过程文档及程序
2020年五一杯数学建模 C题 饲料混合加工问题 原题再现 饲料加工厂需要加工一批动物能量饲料。饲料加工需要原料,如加工猪饲料需要玉米、荞麦、稻谷等。加工厂从不同的产区收购了原料,原料在收购的过程中由于运输、保鲜以及产品本身属性等原因ÿ…...

公益SRC实战|SQL注入漏洞攻略
目录 一、信息收集 二、实战演示 三、使用sqlmap进行验证 四、总结 一、信息收集 1.查找带有ID传参的网站(可以查找sql注入漏洞) inurl:asp idxx 2.查找网站后台(多数有登陆框,可以查找弱口令,暴力破解等漏洞&…...
Word软件手动安装Zotero插件
文章目录 Word软件手动安装Zotero插件方法一方法二 参考资料 Word软件手动安装Zotero插件 方法一 关闭word在zotero中依次点击编辑—首选项—引用—文字编辑软件—重新安装加载项Microsoft word 方法二 寻找Zotero.dotm存储位置, 例如D:\Program Files\Zotero\ext…...
idea 插件推荐第二期
文章目录 便捷开发CodeGlance Pro (代码缩略图)GenerateAllSetter(快速生成对象所有set方法)GsonFormatPlus:json转实体RestfulToolkitX(找到controller快捷请求接口) 美化activate-power-mode-x (敲击计数、动效)Nyan…...

plsql查询中文出现乱码
添加环境变量:如下 变量名:NLS_LANG 变量值:SIMPLIFIED CHINESE_CHINA.ZHS16GBK 变量名:TNS_ADMIN 变量值:D:\instantclient_11_2\network\admin 在Path中添加instantclient_11_2存放路径...

【Docker】五分钟完成Docker部署Java应用,你也可以的!!!
文章目录 前言一、部署步骤1.项目结构2.Dockerfile3.docker-compose.yml4.启动5.常用命令 总结 前言 本文基于Docker Compose部署Java应用,请确保你已经安装了Docker和Docker Compose。 十分钟就能上手docker?要不你也试试? 一、部署步骤 1…...
如何准备2024年的系统设计面试?
1 前言 如果你正在准备软件工程师或软件开发人员的面试,那么你可能知道由于其开放性质和广泛性,准备系统设计是多么困难,但同时你也不能忽略它。在软件工程界,如果你正在申请高级工程师/主管/架构师或更高级别的角色,系统设计是最受追捧的技能,也是整个过程中最重要的环节之一…...

【开源】基于JAVA的电子元器件管理系统
目录 一、摘要1.1 项目简介1.2 项目详细录屏 二、研究内容三、界面展示3.1 登录&注册&主页3.2 元器件单位模块3.3 元器件仓库模块3.4 元器件供应商模块3.5 元器件品类模块3.6 元器件明细模块3.7 元器件类型模块3.8 元器件采购模块3.9 元器件领用模块3.10 系统基础模块 …...
足底筋膜炎怎么治疗治愈
足底筋膜炎又称为跖筋膜炎,跖筋膜主要在足弓下方,它维持足弓稳定性,对于喜欢长期长跑、跳远,或者越野运动,或者部队中的士兵进行拉练,还有需要久坐或者久站的人群中,容易发生跖筋膜炎。治疗方法…...

Keil工程忽略文件.gitignore、自动删除脚本:keilkilll.bat、自动生成目录文件列表脚本
Keil工程忽略文件:.gitignore 忽略规则 *.rar *.o *.d *.crf *.htm *.dep *.map *.bak *.lnp *.lst *.ini *.iex *.sct *.scvd *.dbg* *.uvguix.* *Log.*#忽略.gitignore根目录下的文件夹,根据自己的需要修改 RTE/ Templates/ Examples/ OBJ/#不能忽略…...

软考高级职称哪个好考?明确给你答案
软考考试分为初、中、高三级,其中高级5个方向分别为系统分析师、信息系统项目管理师、网络规划设计师、系统架构设计师、系统规划与管理师。软考高级职称考什么好?有很多人是因为要评高级职称而选择参考软考高级资格考试,那么软考高级里哪个资…...

智能客服外包服务适用于哪些行业?
在当今快节奏的商业环境下,企业需要更高效、更智能且更灵活的客户服务解决方案。而智能客服外包服务正是满足这一需求的利器。不仅可以帮助企业提升客户服务的品质和效率,还能降低企业的运营成本。智能客服外包服务适用于哪些行业呢? 1.电子…...

数字化企业各业务模块模型
1.计划 1.1采购计划执行情况 序号 采购计划号 采购订单号 业务员 供应商 物料 数量 金额 计划入库日期 实际入库日期 状态 针对企业执行中或者未关闭的采购计划进行统计与分析,主要目的在于引领企业员工与领导关注长期在途的采购…...

WPF动画小知识
一、动画合集 创建一个Storyboard演示画板,在画板里对动画进行定义与处理。 常见动画类型 提醒:更多介绍可查看microsoft提供的相关文档 DoubleAnimation //普通Double型控制动画 DoubleAnimationUsingKeyFrames //Dou…...
数据结构 顺序表和链表
1.线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串.. 线性表在逻辑上是线性结构,也就说是连续的一条直线…...
LMI相机配置步骤,使用Gocator2550相机
在此之前可以先浏览我编写的相机SDK通用类和LMISDK,进行配套观看 https://blog.csdn.net/m0_51559565/article/details/134404394 //LMI相机SDK https://blog.csdn.net/m0_51559565/article/details/134403745 //相机通用类1.启动LMI加速器 LMI加速器用于将相机…...

掌握Python中的控制流语句:break, continue, quit的应用技巧详解
引言 在Python编程中,控制流语句是非常重要的一部分,它们可以帮助我们控制程序的执行流程。其中,break、continue和quit是常用的控制流语句,它们可以在循环中起到关键作用。本文将详细介绍这些控制流语句的应用技巧,帮…...
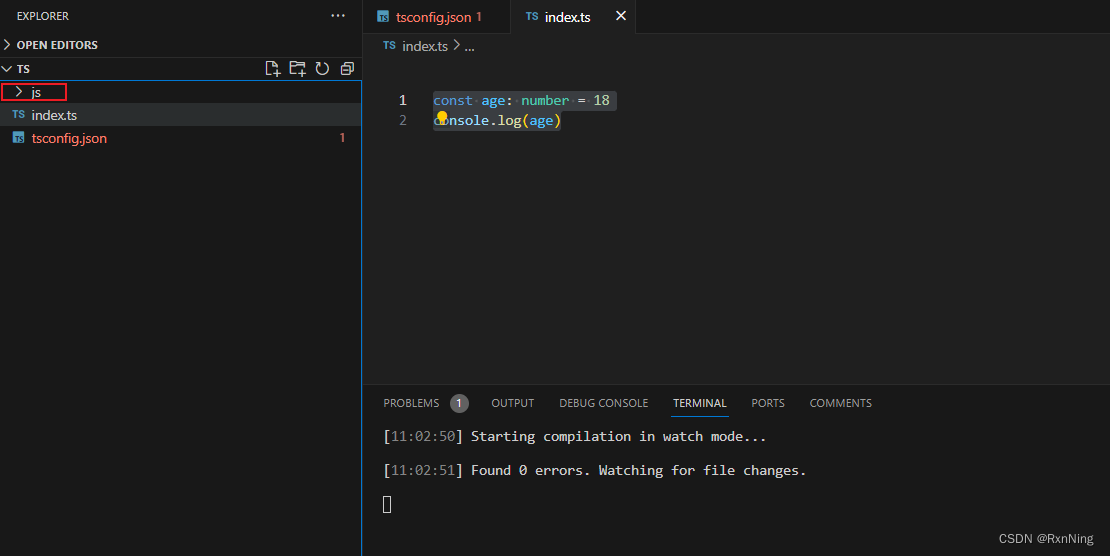
TS手动编译和自动编译方法
把 TS 文件编译成 JS 文件 安装 npm i -g typescript检查是否安装成功 tsc -v方法一 先通过 tsc 把 .ts 文件编译成 .js 文件,再通过 node 把 .js 文件运行 方法二 通过监视配置页面 初始化 tsc --init自动生成一个tsconfig.json 文件 点击进入tsconfig.js…...

【Hello Go】Go语言运算符
Go语言运算符 算术运算符关系运算符逻辑运算符位运算符赋值运算符其他运算符运算符优先级 算术运算符 如果之前没有其他语言基础的小伙伴可以参考下我之前写的C语言运算符讲解 这里主要讲解下Go和C运算符的不同点 – 运算符 Go语言中只有后置 和后置– var a int 5a--fmt.P…...
)
理解 JMeter 聚合报告(Aggregate Report)
Aggregate Report 是 JMeter 常用的一个 Listener,中文被翻译为“聚合报告”。今天再次有同行问到这个报告中的各项数据表示什么意思,顺便在这里公布一下,以备大家查阅。 如果大家都是做Web应用的性能测试,例如只有一个登录的请求…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
