DAY53 1143.最长公共子序列 + 1035.不相交的线 + 53. 最大子序和
1143.最长公共子序列
题目要求:给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
示例 1:
- 输入:text1 = "abcde", text2 = "ace"
- 输出:3
- 解释:最长公共子序列是 "ace",它的长度为 3。
思路
这里不要求子序列是连续的。
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]。这样能够简化数组在第一行和第一列的初始化逻辑。
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;
} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i <= text1.size(); ++i) {for (int j = 1; j <= text2.size(); ++j) {if (text1[i-1] == text2[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;} else {dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}}}return dp[text1.size()][text2.size()];}
};1035.不相交的线
题目要求:我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。
现在,我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且我们绘制的直线不与任何其他连线(非水平线)相交。
以这种方法绘制线条,并返回我们可以绘制的最大连线数。

思路
直线不能相交,这就是说明在字符串A中 找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。
这么分析完之后,大家可以发现:本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!所以直接copy代码就可以了。
- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
53. 最大子序和
题目要求:给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
- 输出: 6
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
思路
dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]。
dp[i]只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
根据dp[i]的定义,很明显dp[0]应为nums[0]即dp[0] = nums[0]。
class Solution {
public:int maxSubArray(vector<int>& nums) {vector<int> dp(nums.size() + 1, 0);dp[0] = nums[0];int result = max(INT_MIN, dp[0]);for (int i = 1; i < nums.size(); ++i) {dp[i] = max(dp[i-1] + nums[i], nums[i]);if (dp[i] > result) result = dp[i];}return result;}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
相关文章:

DAY53 1143.最长公共子序列 + 1035.不相交的线 + 53. 最大子序和
1143.最长公共子序列 题目要求:给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删…...

短剧App开发:个性化的内容推荐
随着移动互联网的普及和用户需求的多样化,短剧App作为一种新兴的内容消费模式,受到了越来越多用户的青睐。在短剧App开发中,个性化的内容推荐是一个重要的功能,它能够根据用户的兴趣偏好和行为数据,为他们提供更精准、…...
互斥量保护资源
一、概念 在多数情况下,互斥型信号量和二值型信号量非常相似,但是从功能上二值型信号量用于同步, 而互斥型信号量用于资源保护。 互斥型信号量和二值型信号量还有一个最大的区别,互斥型信号量可以有效解决优先级反转现 象。 …...
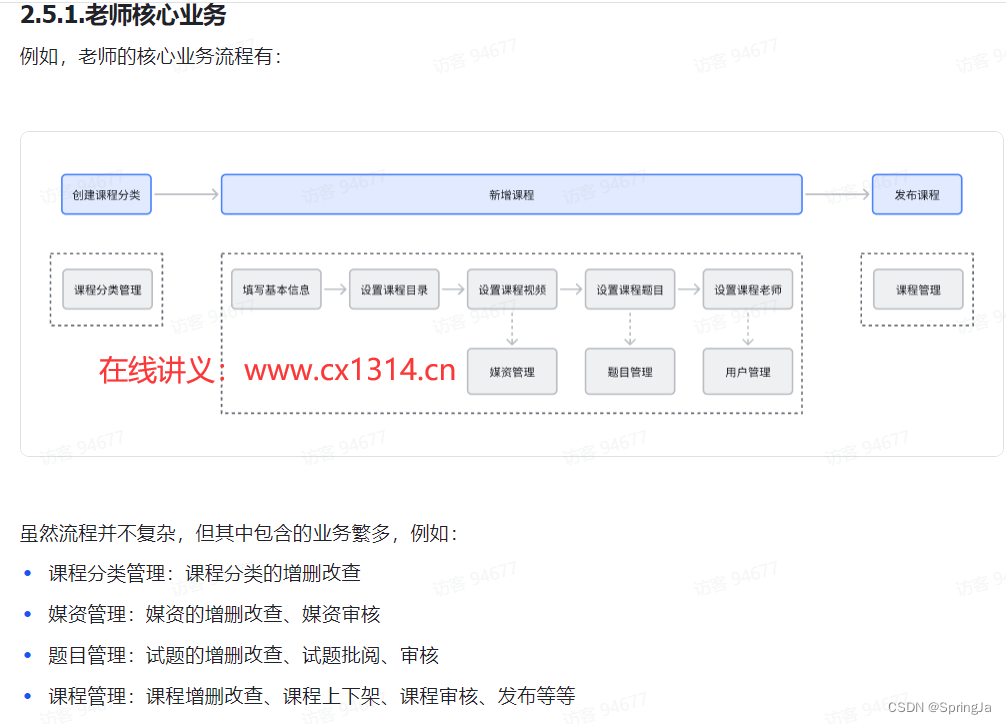
天机学堂-1、项目搭建,微服务架构设计
1.学习背景 各位同学大家好,经过前面的学习我们已经掌握了《微服务架构》的核心技术栈。相信大家也体会到了微服务架构相对于项目一的单体架构要复杂很多,你的脑袋里也会有很多的问号: 微服务架构该如何拆分? 到了公司中我需要自…...
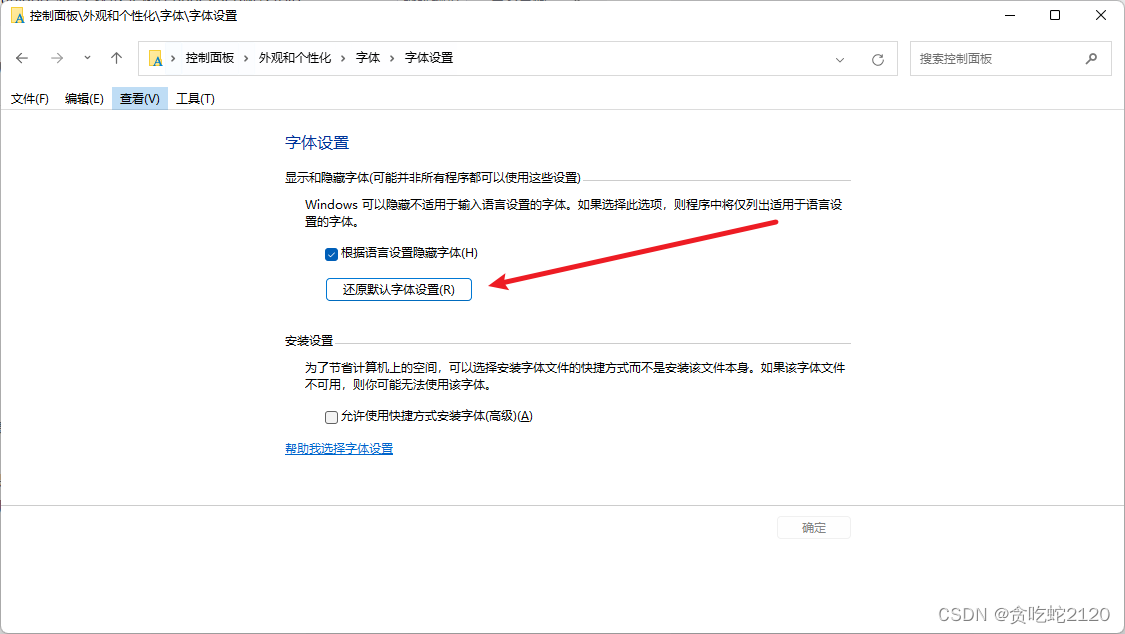
windows 电脑删除不了.TTF的文件
出现这个问题,首先检查,你的.ttf文件是不是在哪个软件中打开了。 如果是,先关掉,然后在删一遍试试。 如果这个还是不行试着打开控制面板>外观和个性化> 字体 > 字体设置>还原默认字体设置勾选,然后重启一下…...
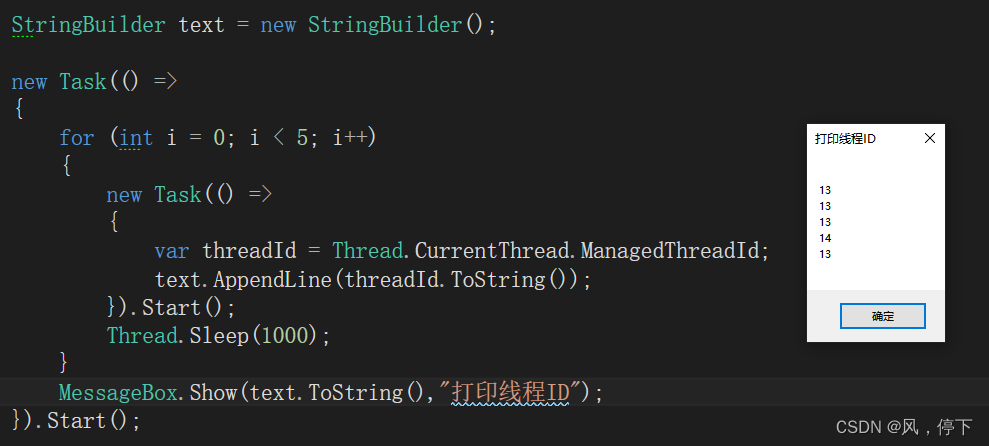
C#多线程的操作
文章目录 1 使用线程意义2 C#线程开启的四种方式2.1 异步委托开启线程2.2 通过Thread类开启线程2.3 通过线程池开启线程2.4 通过任务Task开启线程 3 前台线程和后台线程简述3.1 前台线程3.2 后台线程 4 简述Thread和Task开启线程的区别4.1 Thread效果展示4.2 Task效果展示4.3 区…...

MyBatis Plus—CRUD 接口
Service CRUD 接口 说明: 通用 Service CRUD 封装IService (opens new window)接口,进一步封装 CRUD 采用 get 查询单行 remove 删除 list 查询集合 page 分页 前缀命名方式区分 Mapper 层避免混淆,泛型 T 为任意实体对象建议如果存在自定义通用 Servi…...
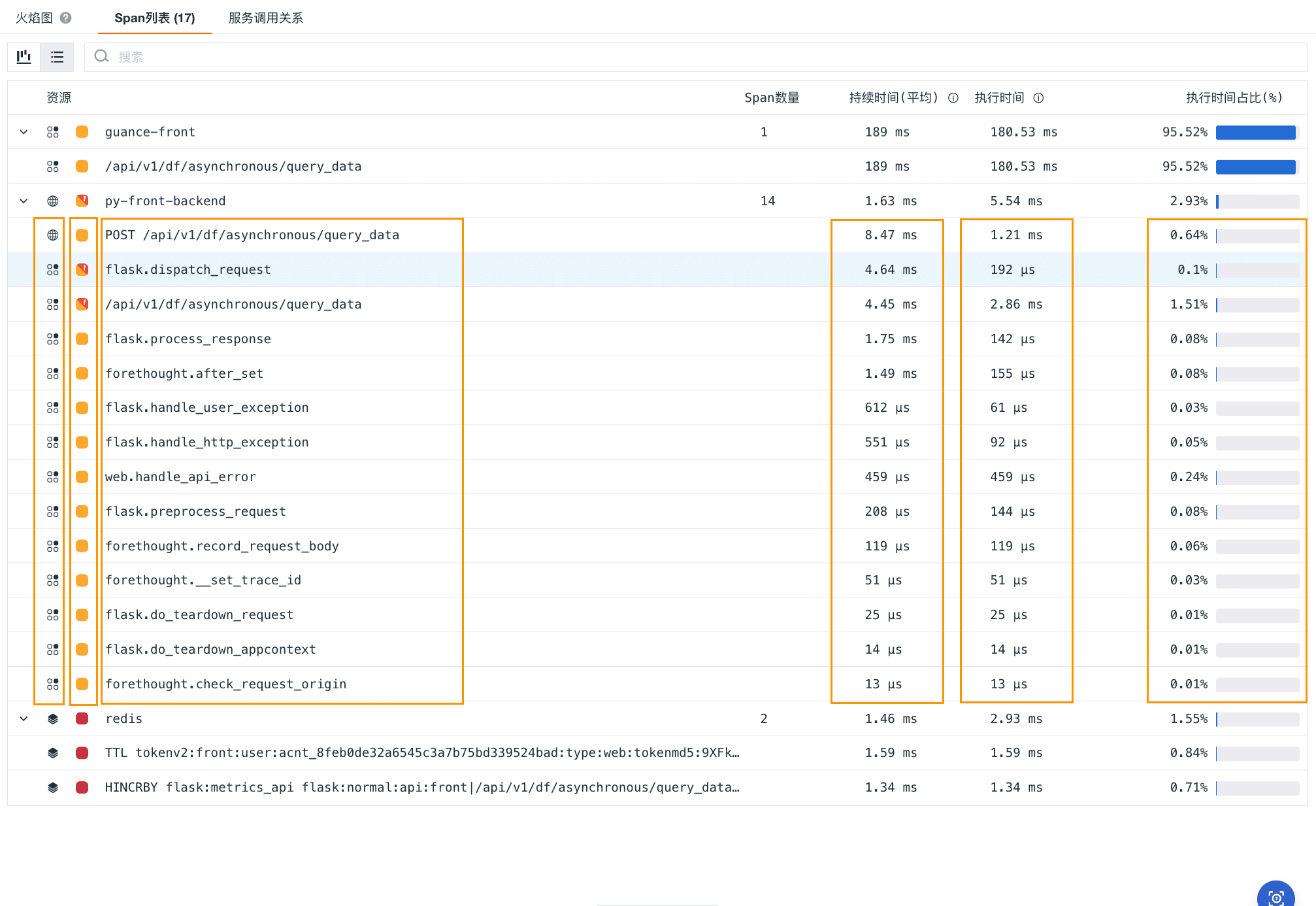
火焰图:链路追踪分析的可视化利器
什么是火焰图? 火焰图用于可视化分布式链路追踪,通过使用持续时间和不同颜色的水平条形来表示请求执行路径中的每个服务调用。分布式跟踪的火焰图包括错误、延迟数据等详情,帮助开发人员识别和解决应用程序中的瓶颈问题。 链路追踪与 Span …...
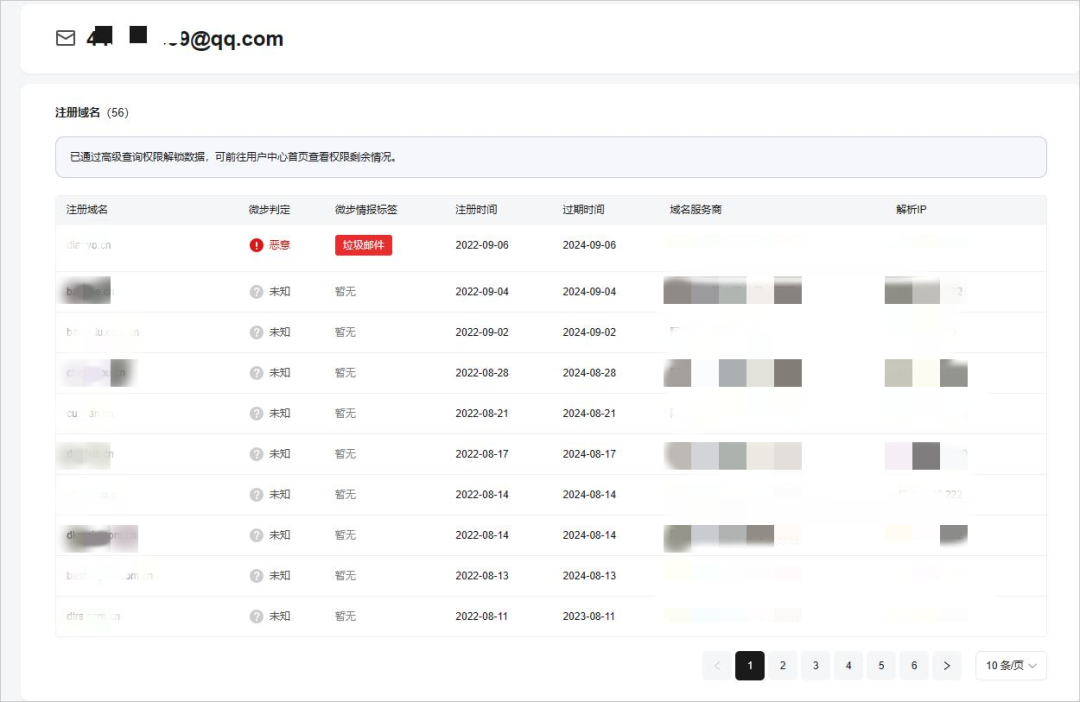
中睿天下Coremail | 2023年Q3企业邮箱安全态势观察报告
10月25日,北京中睿天下信息技术有限公司联合Coremail邮件安全发布《2023年第三季度企业邮箱安全性研究报告》。2023年第三季度企业邮箱安全呈现出何种态势?作为邮箱管理员,我们又该如何做好防护? 以下为精华版阅读,如需…...
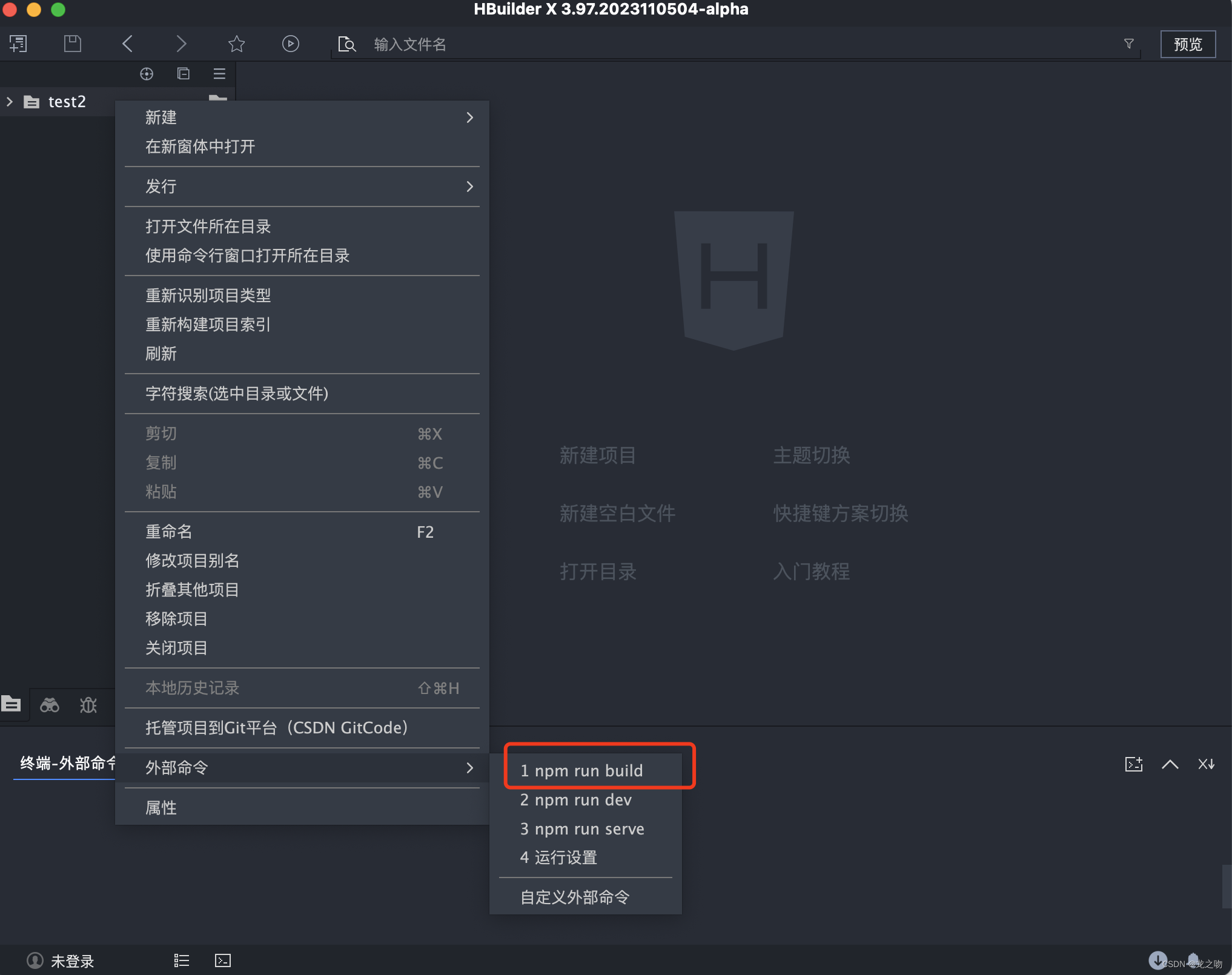
HBuilderX vue项目打包上传到服务器
完成后有个’dist’目录,把真个目录通过FTP 上传到服务器,Mac电脑使用cyberduck 上传 服务器使用‘宝塔’进行一件部署,基本上就是傻瓜式的点击下一步...

2656. K 个元素的最大和 --力扣 --JAVA
题目 给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。你需要执行以下操作 恰好 k 次,最大化你的得分: 从 nums 中选择一个元素 m 。 将选中的元素 m 从数组中删除。 将新元素 m 1 添加到数组中。 你的得分增加 m 。 请你返回执行以上操作恰好 k …...

从HTTP到Tomcat:揭秘Web应用的底层协议与高性能容器
WEB服务器 1. HTTP协议1.1 HTTP-概述1.1.1 介绍1.2.2 特点 2.2 HTTP-请求协议2.3 HTTP-响应协议2.3.1 格式介绍2.3.2 响应状态码 2.4 HTTP-协议解析 2. WEB服务器-Tomcat2.1 简介2.1.1 服务器概述2.1.2 Web服务器2.1.3 Tomcat 2.2 基本使用2.2.1 下载2.2.2 安装与卸载2.2.3 启动…...
百度搜索智能化算力调控分配方法
作者 | 泰来 导读 随着近年深度学习技术的发展,搜索算法复杂度不断上升,算力供给需求出现了爆发式的增长。伴随着AI技术逐步走到深水区,算法红利在逐步消失,边际效应日益显著,算力效能的提升尤为重要,同时随…...

如何搭建接口自动化测试框架?
经过了一年多的接口测试工作,旧的框架也做了一些新的调整,删除了很多冗余的功能,只保留了最基本的接口结构验证、接口回归测试、线上定时巡检功能。 一、框架的演进 界面 UI 做了优化,整个框架的画风突然不一样了(人靠…...
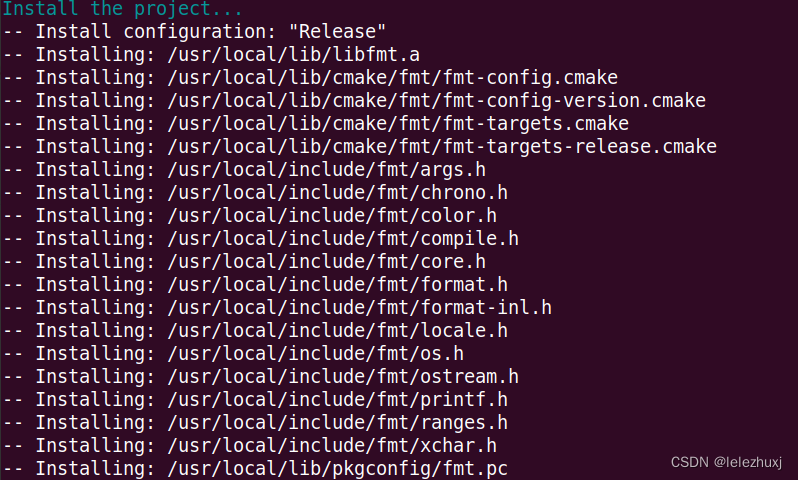
ubuntu 20.04+ORB_SLAM3 安装配库教程
目录 安装ros(如果只是运行ORB-SLAM3,可以跳过安装)0. ros 安装教程1. 安装opencv2. 安装Pangolin3. 安装Eigen34.安装Python & libssl-dev5.安装boost库6.安装ceres库(不必须)7.安装Sophus库(不必须)8. 安装g20库…...
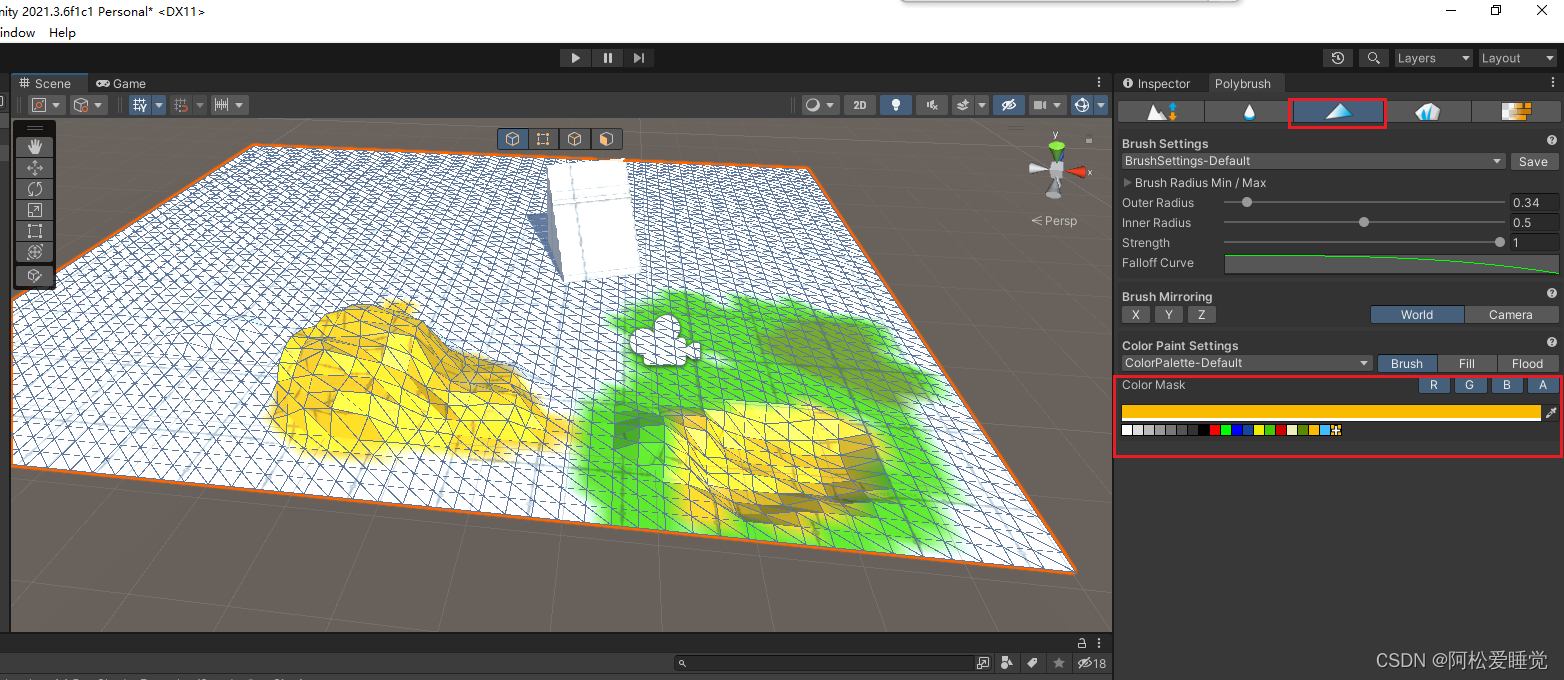
Poly风格模型的创建与使用_unity基础开发教程
Poly风格模型的创建与使用 安装Poly相关组件Poly模型的创建Poly模型编辑 安装Poly相关组件 打开资源包管理器Package Manager 在弹出的窗口左上角Packages选择Unity Registry 搜索框搜索 Poly 搜索结果点击Polybrush 点击右下角 Install 同时也别忘了导入一下模型示例&#…...
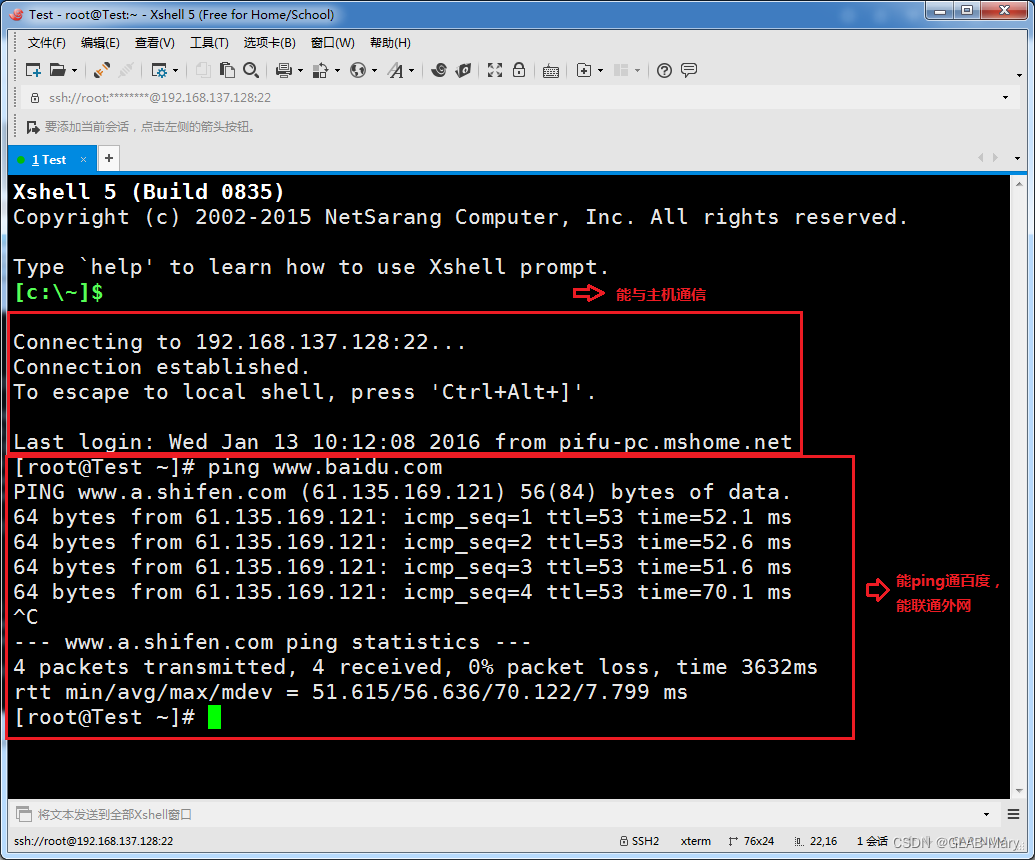
终于有人把VMware虚拟机三种网络模式讲清楚了!
前段时间VMware更新了,你用上最新版了吗? 有几个网工在操作中遇到过各种各样的问题。 比如说由于公司服务器重启导致出现下面的问题:在Xshell里连接虚拟机映射时连接失败;能够连接上虚拟机的映射地址,但git pull时报…...
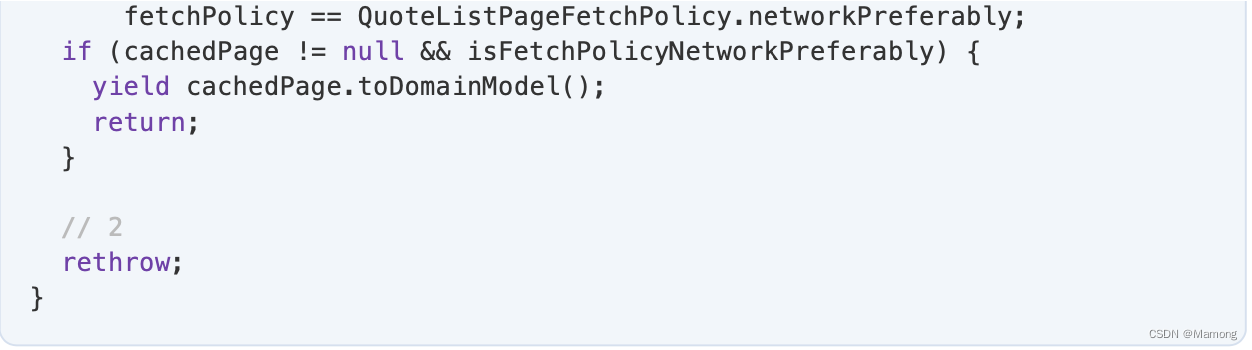
Flutter实践二:repository模式
1.repository 几乎所有的APP,从简单的到最复杂的,在它们的架构里几乎都包括状态管理和数据源这两部分。状态管理常见的有Bloc、Cubit、Provider、ViewModel等,数据源则是一些直接和数据库或者网络客户端进行交互,取得相应的数据&…...
)
交换机Vlan和端口配置(H3C)
交换机Vlan配置(H3C) 配置VLAN配置VLAN接口的IP地址开启ARP网关保护功能,配置被保护的网关IP地址 配置VLAN Vlan物理端口3GigabitEthernet 1/0/1 ~ GigabitEthernet 1/0/14 ;GigabitEthernet 2/0/1 ~ GigabitEthernet 2/0/1450Gi…...

vue自定义指令控制权限
1、在main.js中注册全局指令 import Vue from vue;// 按钮权限控制指令 Vue.directive(permission, {inserted: (el, binding)>{const { value } binding;// 判断当前用户是否拥有该按钮权限if (!checkPermission(value)) {el.parentNode.removeChild(el);}} }); // 判断…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
