Knowledge Graph Reasoning with Relational Digraph
摘要:
知识图推理的目的是从已有的事实中推断出新的事实。基于关系路径的推理方法具有较强的可解释性和可转移性。然而,路径在捕获图中的局部证据方面自然受到限制。在本文中,我们引入了一种新的关系结构,即关系有向图(r-digraph),它由重叠的关系路径组成,用于捕获KG的局部证据。由于图比路径更复杂,如何有效地构建和有效地从中学习是一个挑战。直接编码r-有向图不能很好地扩展,并且在r-有向图中很难捕获与查询相关的信息。我们提出了一种图神经网络的变体,即RED-GNN,以解决上述挑战。具体来说,RED-GNN利用动态规划对具有共享边的多个r-有向图进行递归编码,并利用查询依赖的注意机制选择强相关边。我们证明RED-GNN不仅高效,而且在归纳和转换推理任务中比现有方法都能取得显着的性能提升。此外,RED-GNN中学习到的注意权值可以为KG推理提供可解释的证据。
1.介绍
知识图谱(Knowledge graph, KG)包含了现实世界中物体、人、概念等之间的相互作用,它将人工智能与人类知识联系起来[2,16,18]。相互作用用三种形式(主体实体、关系、客体实体)表示为事实,以表示实体之间的关系。现实世界的kg很大,而且非常不完整[18,44],因此推断新的事实是具有挑战性的。KG推理模拟了这样的过程,从已有的事实中演绎出新的事实[7]。它在语义搜索[4]、推荐[6]、问答[1]等领域有着广泛的应用。在本文中,我们重点学习了在(主题实体、关系、?)形式的查询中进行推理的关系结构。
在过去的十年中,基于三重模型的语义信息学习受到了广泛的关注。这些模型直接对带有实体和关系嵌入的三元组进行推理,如TransE[5]、ConvE[10]、ComplEx[40]、RotatE[36]、QuatE[51]、AutoSF[54]等。由于三元组是独立学习的,它们不能显式地捕获局部证据[26,38,46,48],即查询三元组周围的局部结构,这些结构可以用作KG推理[26]的证据。
路径学习可以帮助更好地捕获图中的局部证据,因为它们可以保持节点之间的顺序连接[13,28]。关系路径是为推理[23]捕获语义和局部证据的第一次尝试。DeepPath [46], MINERVA[9]和M-walk[35]使用强化学习(RL)对与查询有强相关性的关系路径进行采样。由于KGs的稀疏特性,RL方法很难在大规模KGs上进行训练[7]。PathCon[43]对实体之间的所有关系路径进行采样,并使用注意机制对不同路径进行加权,但对于实体查询任务来说代价昂贵。基于规则的方法,如RuleN[25]、Neural LP[48]、DRUM[33]和RNNLogic[29],将关系路径概括为逻辑规则,通过关系的逻辑组合来学习推断关系,并能提供可解释的见解。此外,逻辑规则可以处理推理中存在不可见实体的归纳推理,这在现实应用中很常见[33,48,50]。
在捕获局部证据方面,子图自然比路径提供更多的信息[2,11,45]。它们的有效性已经在基于图的推荐[50,56]和节点表示学习[14]中得到了经验验证。随着图神经网络(graph neural network, GNN)[12,20]在图结构数据建模方面的成功,GNN被引入到KG中的子图结构捕获中。R-GCN[34]、CompGCN[41]和KE-GCN[49]提出通过聚合每层的所有邻居来更新实体的表示。然而,它们不能区分不同邻居的结构作用,也不能解释。DPMPN[47]通过修剪给定查询的不相关实体而不是学习特定的局部结构来学习减少大规模KGs推理的子图的大小。p-GAT[15]联合学习图注意网络和马尔可夫逻辑网络,以弥合嵌入和规则之间的差距。然而,必须预先定义一组规则,并且应该使用昂贵的em算法进行优化。最近,GraIL[38]提出了从局部封闭子图预测关系的方法,并展示了子图的归纳能力。然而,由于封闭子图的限制,它的有效性和效率都存在问题。
受基于路径的方法的可解释和可转移能力以及子图的结构保持特性的启发,我们在KG中引入了一种新的关系结构,称为r-有向图,以结合两者的优点。有向图通过保留重叠的关系路径和推理的关系结构,将关系路径推广到子图。与结构简单的关系路径不同,如何高效地构建r-有向图并从中学习是一个挑战,因为构建过程是昂贵的[38,43]。受动态规划节省重叠子问题计算成本的启发,我们提出了GNN[12]的变体RED-GNN,该算法递归编码具有共享边的多个关系有向图(r- digraps),并通过查询依赖的关注权选择强相关边。从经验上看,RED-GNN在归纳和传导基准测试中都比最先进的推理方法有了显著的进步。此外,训练和推理过程效率高,模型参数数量少,学习到的结构具有可解释性。
2.相关工作

2.1 Path-based methods
关系路径(定义1)是一组按顺序连接的三元组。基于路径的方法学习通过一组关系路径作为本地证据来预测三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎)。DeepPath[46]通过强化学习(RL)学习生成从𝑒𝑞到𝑒𝑎的关系路径。为了提高效率,MINERVA[9]和M-walk[35]通过RL学习生成从𝑒𝑞开始的多条路径。得分由不同𝑒𝑎的到达频率表示。由于KG结构复杂,奖励非常稀疏,很难训练RL模型[7]。PathCon[43]对连接两个实体的所有路径进行采样,以预测它们之间的关系,这对于推理任务来说是昂贵的(𝑒𝑞,𝑟𝑞,𝑒𝑎)。
定义1(关系路径[24,46,53])。长度为𝐿的关系路径是一组𝐿三元组(𝑒0,𝑟1,𝑒1),(𝑒1,𝑟2,𝑒2),…(𝑒𝐿−1,𝑟𝐿,𝑒𝐿),按顺序连接头部到尾部。
与直接使用路径不同,基于规则的方法将逻辑规则作为关系路径的一般形式来学习。逻辑规则是由一组关系组合而成的,用来推断一个特定的关系。这可以提供更好的解释,并可以转移到看不见的实体。通过挖掘方法(如RuleN[25])、EM算法(如RNNLogic[29])或端到端训练(如Neural LP[48]和DRUM[33])来学习规则,以生成𝑒𝑞和𝑒𝑎之间高度相关的关系路径。规则可以提供逻辑解释并转移到不可见的实体。然而,这些规则只捕获序列证据,因此无法学习更复杂的模式,如子图结构。
2.2 GNN-based methods
如第1节所述,子图可以保留比关系路径更丰富的信息,因为子图中允许更多的度。GNN在图形结构化数据[2]建模方面显示出强大的能力。这启发了最近的工作,如RGCN [34], CompGCN[41]和KE-GCN[49],将GNN扩展到KG上,将消息传递框架[12]下的实体和关系表示聚合为:
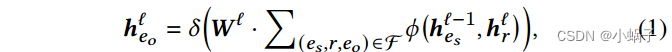
其中聚合(·,·)维度为𝑑的实体𝑒𝑜的1跳相邻边(𝑒𝑠,𝑟,𝑒𝑜)∈F上的消息。𝑾ℓ∈R𝑑×𝑑是一个加权矩阵,𝛿激活函数和𝒉ℓ𝑟关系表示在ℓ层。在𝐿层聚合之后,表示方式![]() 捕获实体𝑒∈V的局部结构与解码器评分函数共同工作来测量三元组。由于消息传递函数(1)聚集了所有邻居的信息,并且与查询无关,因此R-GCN和CompGCN无法捕获特定查询的显式本地证据,并且不可解释。
捕获实体𝑒∈V的局部结构与解码器评分函数共同工作来测量三元组。由于消息传递函数(1)聚集了所有邻居的信息,并且与查询无关,因此R-GCN和CompGCN无法捕获特定查询的显式本地证据,并且不可解释。
DPMPN[47]没有使用所有的邻域,而是设计了一个GNN来聚合实体的嵌入,另一个GNN来动态地扩展和修剪查询实体𝑒𝑞的推理子图。在采样实体上应用查询相关的注意以进行修剪。该方法通过注意流在被修剪的子图上显示了可解释的推理过程,但仍然需要嵌入来指导修剪,因此不能推广到看不见的实体。此外,它不能捕获支持给定查询三元组的显式本地证据。
p-GAT[15]和pLogicNet[30]通过变分em算法共同学习基于嵌入的模型和马尔可夫逻辑网络(MLN)。嵌入模型生成证据供MLN进行更新,MLN扩展训练数据供嵌入模型进行训练。MLN带来了嵌入模型和逻辑规则之间的差距,但它需要一组预定义的规则进行初始化,并且使用变分em算法的训练成本很高。
最近,GraIL[38]提出提取查询实体𝑒𝑞和应答实体𝑒𝑎之间的封闭子图G(𝑒𝑞,𝑒𝑎)。为了学习封闭子图,在G(𝑒𝑞,𝑒𝑎)中的边上应用具有查询依赖注意力的关系GNN[34],以控制不同查询边的重要性,但学习到的注意力权重是不可解释的(见附录B)。在𝐿层聚合之后,图级表示聚合子图中的所有实体𝑒∈V,并用于对三重(𝑒𝑞,𝑟𝑞,𝑒𝑎)进行评分。由于需要显式地提取子图并为不同的三元组评分,因此计算成本非常高。
3.关系有向图(r-digraph)
关系路径在KGs上显示出很强的可转移和可解释推理能力[9,33,48]。然而,它们在捕获KG中更复杂的依赖关系方面受到限制,因为路径中的节点只能按顺序连接。基于gnn的方法可以学习不同的子图结构。但是现有的方法都不能有效地学习到规则一样既可解释又可归纳的子图结构。因此,我们有动力去定义一种新的结构,去探索重要的局部证据。
在定义有向图之前,我们首先在定义2中介绍一种特殊类型的有向图。
定义2(layered st-GRAPH[3])。The layered st-graph是一个只有一个源节点(s)和一个汇聚节点(t)的有向图,所有的边都是有向的,连接连续层之间的节点,从𝑙-th层指向𝑙+ 1-th层。
在这里,我们采用一般方法用逆关系和恒等关系扩充三元组[33,41]。那么,所有在𝑒𝑞和𝑒𝑎之间长度小于或等于𝐿的关系路径都可以表示为长度为𝐿的关系路径![]() 。这样,它们可以在分层的st图中形成路径,单个源实体𝑒𝑞和接收实体𝑒𝑎。这种结构保留了𝑒𝑞和𝑒𝑎之间的所有关系路径,长度为𝐿,并维护了子图结构。基于这个观察,我们在定义3中定义了r-有向图。
。这样,它们可以在分层的st图中形成路径,单个源实体𝑒𝑞和接收实体𝑒𝑎。这种结构保留了𝑒𝑞和𝑒𝑎之间的所有关系路径,长度为𝐿,并维护了子图结构。基于这个观察,我们在定义3中定义了r-有向图。
定义3 (r-digraph)。有向图![]() 是具有源实体𝑒𝑞和接收实体𝑒𝑎的分层st图。同一层中的实体彼此不同。在r-有向图中,任何从𝑒𝑞到𝑒𝑎的路径都是一条长度为𝐿的关系路径
是具有源实体𝑒𝑞和接收实体𝑒𝑎的分层st图。同一层中的实体彼此不同。在r-有向图中,任何从𝑒𝑞到𝑒𝑎的路径都是一条长度为𝐿的关系路径![]() ,其中
,其中![]() 将一个在𝑙−1层的实体连接到一个在𝑙层的实体。如果不存在连接𝑒𝑞和𝑒𝑎且长度为𝐿的关系路径,则定义
将一个在𝑙−1层的实体连接到一个在𝑙层的实体。如果不存在连接𝑒𝑞和𝑒𝑎且长度为𝐿的关系路径,则定义![]() 。
。
图1(b)提供了一个r-有向图![]() 的示例,用于在图1(a)的示例KG中推断新的三重
的示例,用于在图1(a)的示例KG中推断新的三重![]() 。受关系路径推理能力的启发[9,33,48],我们的目标是利用r-有向图进行KG推理。然而,与序列模型学习结构简单的关系路径不同[9,46],如何高效地构建和有效地从r-有向图中学习是一个挑战。
。受关系路径推理能力的启发[9,33,48],我们的目标是利用r-有向图进行KG推理。然而,与序列模型学习结构简单的关系路径不同[9,46],如何高效地构建和有效地从r-有向图中学习是一个挑战。
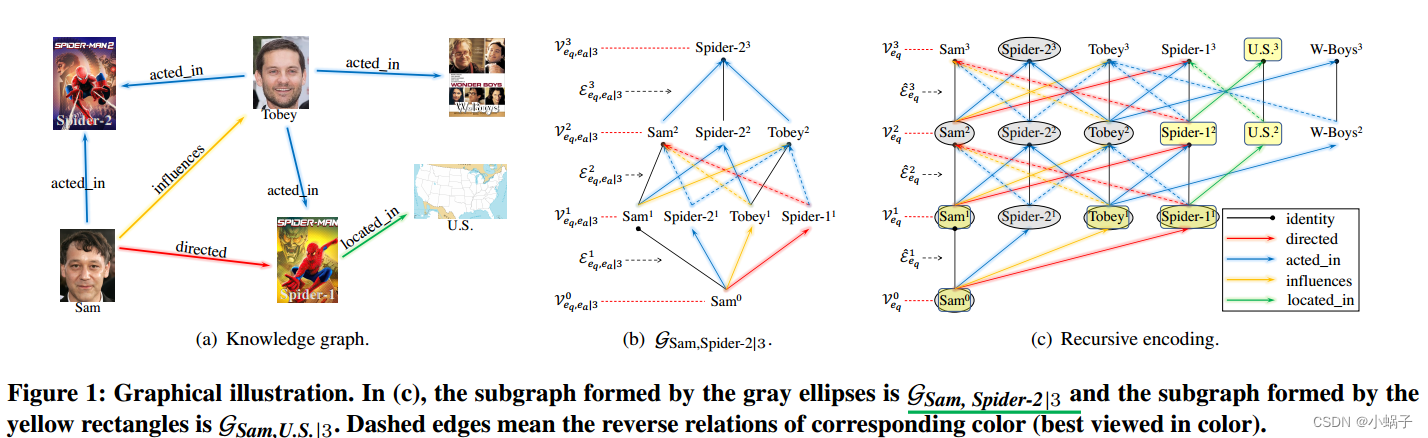
图1:图形化说明。在(c)中,由灰色椭圆组成的子图为GSam, Spider-2 bbbb3,由黄色矩形组成的子图为GSam,U.S. bbbb3。虚线边表示对应颜色的反向关系(以彩色观看效果最好)。

4 .提出的模型
在这里,我们展示了如何定制gnn来高效和有效地从r-有向图中学习。提取子图结构,然后学习子图表示是文献中子图编码的常见做法,例如GraphSage[14]和GraIL[38]。给定一个查询三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎),子图编码通常包含三个过程:
- 分别提取𝑒𝑞和𝑒𝑎的邻域;
- 取交点构造子图;
- 运行消息传递并使用图级表示作为子图编码。
在处理r-有向图![]() 时,可以在算法1中自定义相同的方法。首先,我们在步骤2-5中得到
时,可以在算法1中自定义相同的方法。首先,我们在步骤2-5中得到![]() 的邻域。其次,我们在步骤6-8中取
的邻域。其次,我们在步骤6-8中取![]() 的邻域的交集,以诱导r-有向图
的邻域的交集,以诱导r-有向图![]() 层。第三,如果r-有向图为空,我们在步骤9中将表示设置为0。否则,在步骤10-12中逐层进行消息传递。由于
层。第三,如果r-有向图为空,我们在步骤9中将表示设置为0。否则,在步骤10-12中逐层进行消息传递。由于![]() 是single sink实体,因此使用最后一层表示方式
是single sink实体,因此使用最后一层表示方式![]() 作为子图表示来编码r-有向图
作为子图表示来编码r-有向图![]() 。我们将这个简单的解决方案命名为RED-Simp。
。我们将这个简单的解决方案命名为RED-Simp。

然而,算法1是非常昂贵的。首先,我们需要进行步骤3和步骤4的两个方向采样,取交点提取r-有向图。其次,给定一个查询(𝑒𝑞,𝑟𝑞,?),我们需要对|V|不同的三元组和不同的应答实体𝑒𝑎∈V执行此算法。它需要![]() 时间(见4.3节)来预测给定查询(𝑒𝑞,𝑟𝑞,?),其中𝐷¯是V中实体的平均度数,
时间(见4.3节)来预测给定查询(𝑒𝑞,𝑟𝑞,?),其中𝐷¯是V中实体的平均度数,![]() 是边的平均个数在
是边的平均个数在![]() 。这些限制也存在于PathCon[43]和GraIL[38]。为了提高效率,我们建议对多个数据进行编码在4.1节中递归地使用r-有向图。
。这些限制也存在于PathCon[43]和GraIL[38]。为了提高效率,我们建议对多个数据进行编码在4.1节中递归地使用r-有向图。
4.1 Recursive r-digraph encoding
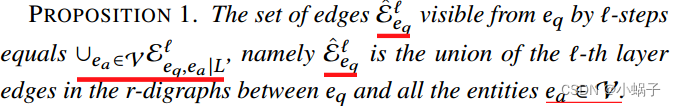
命题1指出,具有不同答案实体![]() 的第𝑙层边
的第𝑙层边![]() 在
在![]() 中共享同一边集。一种节省重叠子问题计算量的常用方法是动态规划。这已被用于在大规模图[14]上聚合节点表示,或在KGs[52]上传播问题表示。受动态规划效率的启发,我们递归地构造了𝑒𝑞和任意实体𝑒𝑜之间的向图:
中共享同一边集。一种节省重叠子问题计算量的常用方法是动态规划。这已被用于在大规模图[14]上聚合节点表示,或在KGs[52]上传播问题表示。受动态规划效率的启发,我们递归地构造了𝑒𝑞和任意实体𝑒𝑜之间的向图:
![]()
一旦表示![]() 的所有实体
的所有实体![]() 在ℓ−1-th层都准备好了,我们可以编码
在ℓ−1-th层都准备好了,我们可以编码![]() 结合
结合![]() 与共享边缘
与共享边缘![]() 在ℓ-th层。基于命题1和Eq.(2),我们被激励对多个r-有向图进行递归编码,这些r-有向图在
在ℓ-th层。基于命题1和Eq.(2),我们被激励对多个r-有向图进行递归编码,这些r-有向图在![]() 中具有共享边。整个过程在算法2中。
中具有共享边。整个过程在算法2中。

最初,在![]() 中只有
中只有![]() 可见。在第1层中,我们在第3步中收集边缘
可见。在第1层中,我们在第3步中收集边缘![]() 和实体
和实体![]() 。然后,对传递的消息进行约束,通过
。然后,对传递的消息进行约束,通过![]() 中的边得到
中的边得到![]() 的表示。最后,表示
的表示。最后,表示![]() ,
,![]() 。递归编码在
。递归编码在![]() 中的共享边更有效,循环更少。它学习与算法1相同的表示,这是由命题2保证的。
中的共享边更有效,循环更少。它学习与算法1相同的表示,这是由命题2保证的。
命题2。给定相同的三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎),算法1和算法2编码的结构是相同的。
4.2 Interpretable reasoning with r-digraph
由于![]() 的构造与查询关系𝑟𝑞是独立的,因此如何对𝑟𝑞进行编码是另一个需要解决的问题。给定共享相同r-有向图的不同三元组,例如
的构造与查询关系𝑟𝑞是独立的,因此如何对𝑟𝑞进行编码是另一个需要解决的问题。给定共享相同r-有向图的不同三元组,例如![]() 和
和![]() ,我们用于推理的局部证据是不同的。为了从r-有向图中获取查询相关知识并发现可解释的局部证据,我们使用注意机制[42]并将𝑟𝑞编码为注意权值,以控制
,我们用于推理的局部证据是不同的。为了从r-有向图中获取查询相关知识并发现可解释的局部证据,我们使用注意机制[42]并将𝑟𝑞编码为注意权值,以控制![]() 中不同边的重要性。消息传递函数指定为:
中不同边的重要性。消息传递函数指定为:
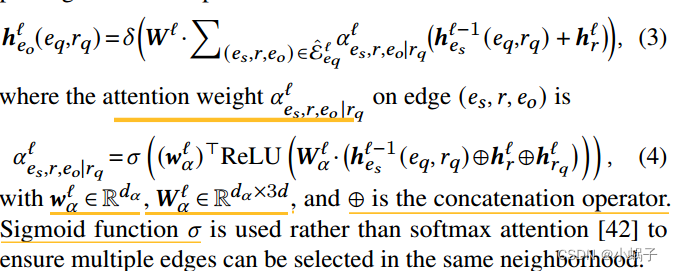 为了保证在同一邻域内可以选择多条边,采用了s型函数而不是softmax关注[42] 。
为了保证在同一邻域内可以选择多条边,采用了s型函数而不是softmax关注[42] 。
通过(3)对𝐿层进行聚合后,表示![]() 可以编码得分的基本信息(𝑒𝑞,𝑟𝑞,𝑒𝑎)。因此,我们设计了一个简单的评分函数:
可以编码得分的基本信息(𝑒𝑞,𝑟𝑞,𝑒𝑎)。因此,我们设计了一个简单的评分函数:
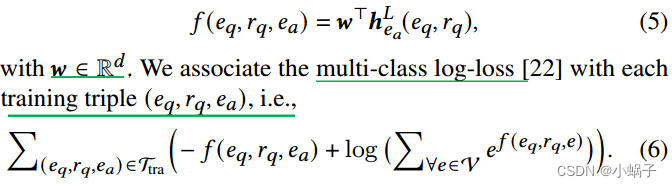
(6)中的第一部分是![]() (训练查询集)中正三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎)的分数,第二部分包含具有相同查询的所有三元组(𝑒𝑞,𝑟𝑞,?)的分数。模型参数
(训练查询集)中正三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎)的分数,第二部分包含具有相同查询的所有三元组(𝑒𝑞,𝑟𝑞,?)的分数。模型参数 ![]() 随机初始化,并通过随机梯度下降[19]最小化(6)进行优化。
随机初始化,并通过随机梯度下降[19]最小化(6)进行优化。
我们提供定理1来证明,如果一组关系路径与查询三元组强相关,则它们可以通过RED-GNN中的注意权值来识别,因此是可解释的。这个定理在第5.4节中也有实证说明。

4.3 Inference complexity
在这一部分中,我们比较了不同基于gnn的方法的推理复杂度。在对查询(𝑒𝑞,𝑟𝑞,?)进行推理时,我们需要用不同的答案实体![]() 对
对![]() 三元组求值,我们假设平均度为
三元组求值,我们假设平均度为![]() ,r-有向图每层的平均边数为
,r-有向图每层的平均边数为![]() 。
。

5.EXPERIMENTS
所有实验都是用PyTorch框架[27]用Python编写的,并在具有11GB内存的RTX 2080Ti GPU上运行。
5.1 Inductive reasoning
归纳推理是一个热门的研究课题[14,33,38,48],因为在现实世界的应用中不断出现新的实体,如新用户、新项目和新概念[50]。为了能够对看不见的实体进行推理,需要模型捕捉语义和局部证据,而忽略实体的身份。
Setup


Tie policy
在评价中,Tie policy很重要。具体来说,当有相同秩的三元组时,在平局中选择最大秩和最小秩将导致相当不同的结果[37]。考虑到我们对![]() 的三元组给予相同的分数,会有Tie policy政策的顾虑。因此,我们使用tie中三元组的平均排名,如建议的[31]
的三元组给予相同的分数,会有Tie policy政策的顾虑。因此,我们使用tie中三元组的平均排名,如建议的[31]
数据集
我们使用[38]中的基准数据集,分别在WN18RR[10]、FB15k237[39]和NELL-995[46]上创建。每个数据集包括四个版本,其中包含不同组的三元组。详情请参阅[38]。
结果
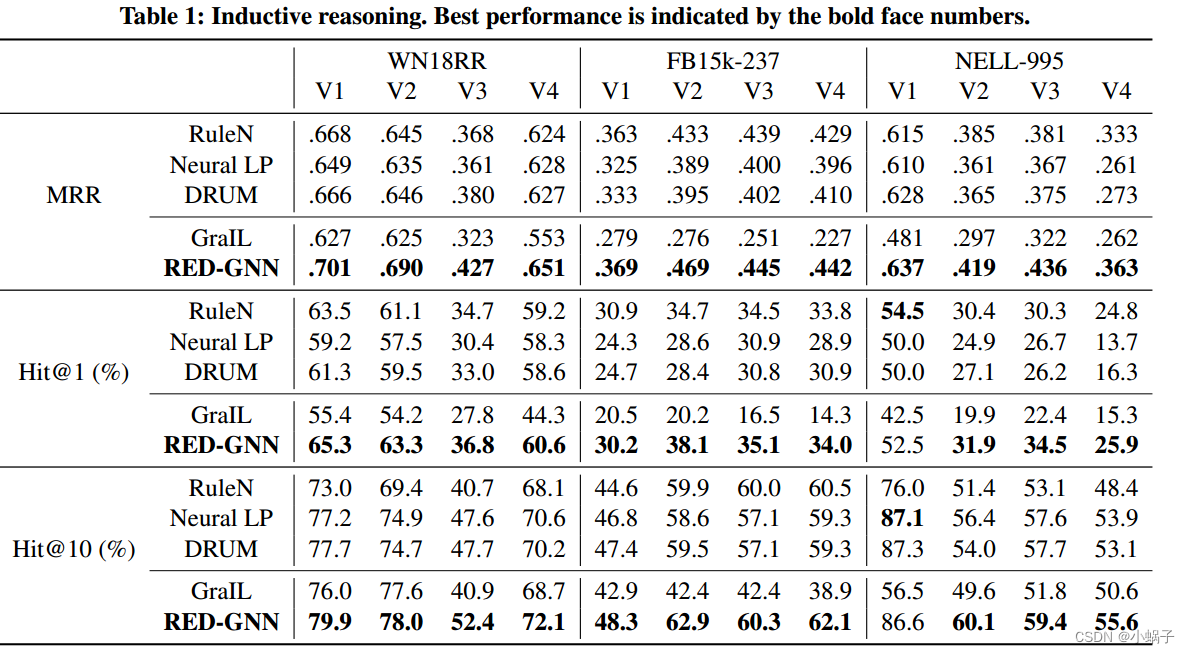
性能如表1所示。首先,GraIL是所有方法中最差的,因为封闭子图不能很好地学习可以推广到看不见的实体的关系结构(详见附录B)。其次,在基于规则的方法中没有绝对的赢家,因为不同的规则适应不同的数据集。相比之下,RED-GNN在所有基准测试中都优于基线。在定理1的基础上,注意权值有助于自适应地学习不同数据集的相关关系路径,同时保留结构模式。在某些情况下,RED-GNN的Hit@10比基于规则的方法略差,因为它可能会对排名靠前的样本过拟合。
5.2 Transductive reasoning
传导推理,也称为KG补全[40,44],是文献中的另一种一般设置。它评估了模型在不完整KG上学习模式的能力。
设置。在此设置中,给出了![]() 和查询三元组
和查询三元组![]() ,并通过反向关系进行增广。对于基于三元组的方法,
,并通过反向关系进行增广。对于基于三元组的方法,![]() 中的三元组用于训练,
中的三元组用于训练,![]() 用于推理。对于其他的,使用F中3/4的三元组提取路径/子图来预测训练中剩下的1/4三元组,然后使用完整的集合F来预测推理中的
用于推理。对于其他的,使用F中3/4的三元组提取路径/子图来预测训练中剩下的1/4三元组,然后使用完整的集合F来预测推理中的![]() [33,48]。我们在第5.1节中使用相同的过滤排名指标和相同的关联策略,即MRR, Hit@1和Hit@10。
[33,48]。我们在第5.1节中使用相同的过滤排名指标和相同的关联策略,即MRR, Hit@1和Hit@10。
基线。我们将RED-GNN与基于三重的ConvE[10]、RotatE[36]和QuatE[51]方法进行了比较;基于路径的方法MINERVA[9]、Neural LP[48]、DRUM[33]和RNNLogic[29];基于mln的方法pLogicNet[30]和基于gnn的方法CompGCN[41]和DPMPN[47]。这里没有比较RuleN[25],因为在这个设置中,它比DRUM[33]和RNNLogic[29]更差。p-GAT不进行比较,因为它们的结果是在有问题的框架[37]上评估的。没有比较GraIL[38],因为它在大型图上计算难以处理(参见第5.3节)。
Hyper-parameters。RED-GNN超参数的调谐范围与归纳推理中的调谐范围相同。对于RotatE和QuatE,我们调整维度为{100,200,500,1000},批大小为{256,512,1024,2048},权重衰减为[10−5,10−2],负样本数为{64,128,256,512,1024},训练迭代为100000。对于MINERVA, Neural LP, DRUM和DPMPN,我们使用它们提供的默认设置。对于CompGCN,我们选择解码器为ConvE,算子为建议的循环相关[41],并调整学习率为[10−4,10−2],层为{1,2,3},辍学率为[0,0.3],训练epoch为300。
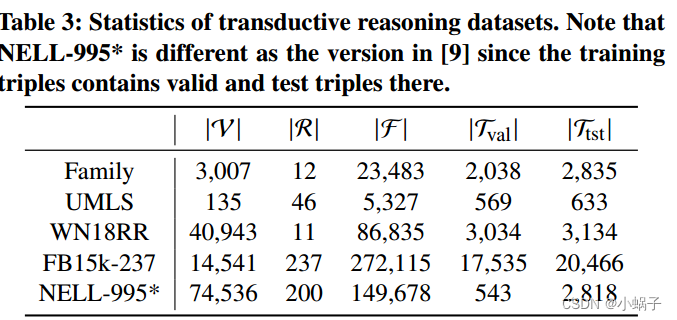
数据集。使用了Family[21]、UMLS[21]、WN18RR[10]、FB15k237[39]和NELL-995[46] 5个2数据集。我们在表3中提供了实体、关系和三元组分割的统计信息。
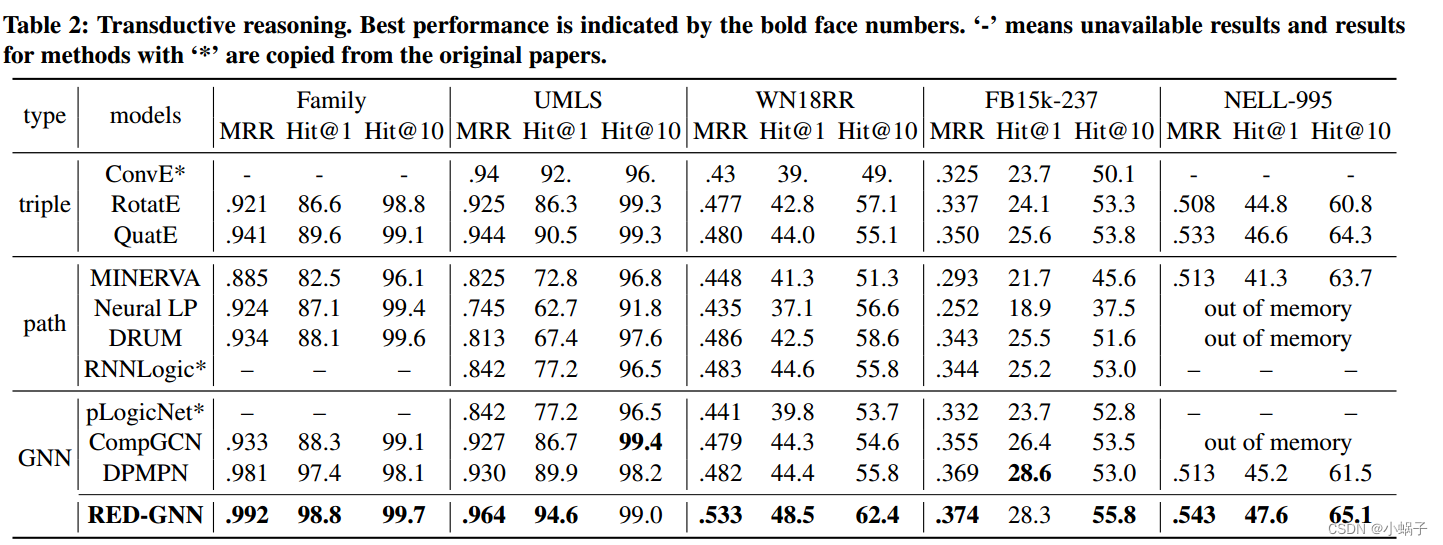
结果。如表2所示,基于三元组的方法在Family和UMLS上优于基于路径的方法,在WN18RR、FB15k-237上与DRUM和RNNLogic相当。实体嵌入可以隐式地保留实体周围的局部信息,而基于路径的方法可能会丢失结构模式。CompGCN的性能与基于三元组的方法类似,主要依赖于聚合嵌入和解码器评分函数。Neural LP, DRUM和CompGCN在NELL-995上使用74个𝑘实体,由于使用完全邻接矩阵而耗尽内存。对于DPMPN,剪枝子图中的实体信息量比CompGCN更大,因此具有更好的性能。对于RED-GNN,它优于MRR指标所指示的所有基线。这表明,r-有向图不仅可以很好地转移到看不见的实体,而且可以在不使用实体嵌入的情况下捕获不完整kg中的重要模式。
5.3 Complexity analysis
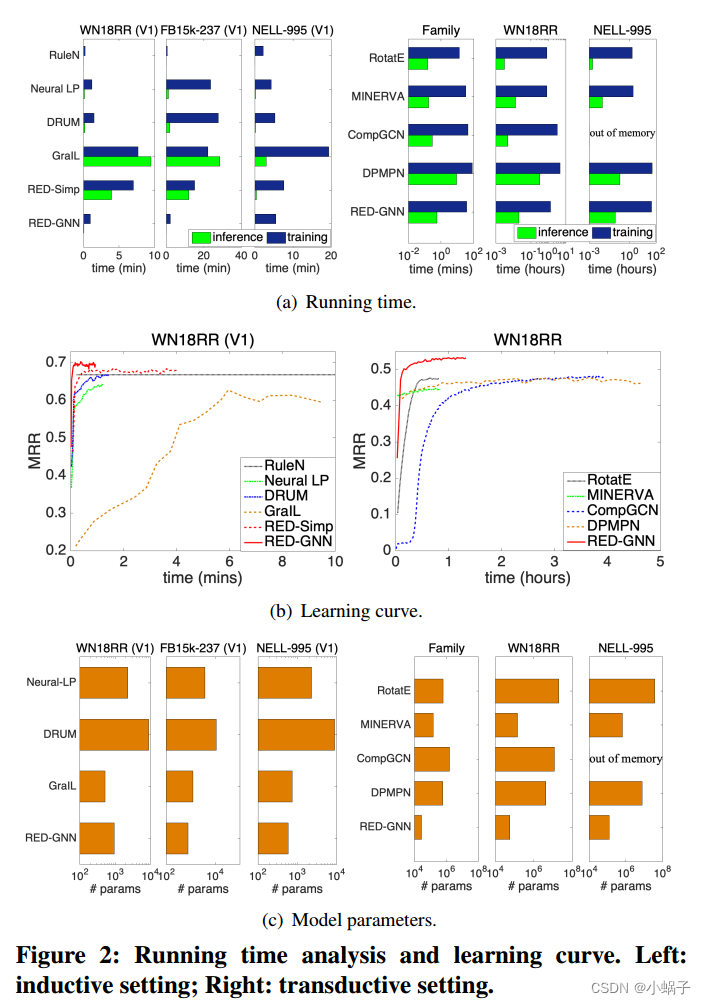
在这一部分中,我们从运行时间和参数大小两个方面比较了不同方法的复杂度。我们在图2(a)中显示了每种方法的训练时间和Ttst上的推理时间,在图2(b)中显示了学习曲线,在图2(c)中显示了模型参数。
归纳推理。我们比较了RuleN、Neural LP、DRUM、GraIL和RED-GNN对WN18RR (V1)、FB15k-237 (V1)和NELL-995 (V1)的影响。在RuleN中,训练和推理都非常高效。Neural LP和DRUM的开销相似,但使用全邻接矩阵比RED-GNN的开销更大。对于GraIL,训练和推理都是非常昂贵的,因为它们需要双向采样来提取子图,然后为每个三元组进行计算。在模型参数方面,RED-GNN和GraIL的参数数量相近,均少于Neural-LP和DRUM。总的来说,RED-GNN比Neural LP、DRUM和GraIL的可微方法更有效。
转换推理。我们比较了RotatE、MINERVA、CompGCN、DPMPN和RED-GNN对Family、WN18RR和NELL-995的影响。由于简单的三元组训练框架,旋转是最快的方法。MINERVA比基于gnn的方法更有效,因为采样路径可以有效地按顺序建模。CompGCN的层数更少,与RED-GNN的成本相似,因为它的计算是在整个图上进行的。对于DPMPN,剪枝是昂贵的,并且它有两个gnn一起工作,因此它比RED-GNN更昂贵。GraIL比RED-GNN贵上几百倍,因此在这种情况下,在更大的千克数上是难以处理的。由于RED-GNN不学习实体嵌入,因此与其他四种方法相比,它的参数要少得多。
5.4 Case study: learned r-digraphs
我们在Family和UMLS数据集上使用𝐿=3的RED-GNN可视化了一些范例学习的r-有向图。给定三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎),我们删除G𝑒𝑞,𝑒𝑎|𝐿中关注权值小于0.5的边,并提取其余部分。图3(a)显示了DRUM失败的一个三重情况。如图所示,将id-1482推断为id-1480的儿子需要知道id-1480是本地结构中叔叔id-1432的唯一兄弟。图3(b)显示了具有相同的𝑒𝑞和𝑒𝑎的示例,它们共享相同的有向图G𝑒𝑞,𝑒𝑎|𝐿。如图所示,RED-GNN可以为不同的查询关系学习不同的结构,这符合定理1。图3中的示例表明RED-GNN是可解释的。我们在附录A中提供了更多的示例和可视化算法。
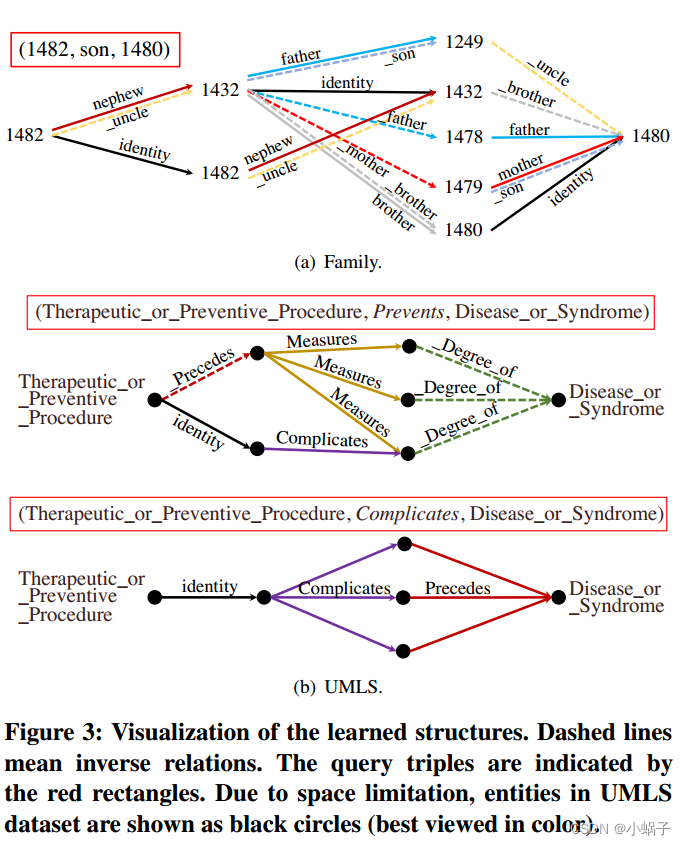
图3:学习结构的可视化。虚线表示反比关系。查询三元组由红色矩形表示。由于空间限制,UMLS数据集中的实体显示为黑色圆圈(最好以彩色显示)。
5.5 Ablation study
RED-GNN的变体。表4显示了不同变体的性能。首先,我们研究了移除𝑟𝑞对注意力的影响(记为Attn-w.o.-𝑟𝑞)。具体来说,我们删除![]() 从关注权重
从关注权重![]() in (4)和改变评分函数
in (4)和改变评分函数![]() 。由于关注
。由于关注![]() 的目的是找出
的目的是找出![]() 中的重要边,因此在没有查询关系控制𝑟𝑞的情况下,学习到的结构信息量不足,性能较差。
中的重要边,因此在没有查询关系控制𝑟𝑞的情况下,学习到的结构信息量不足,性能较差。
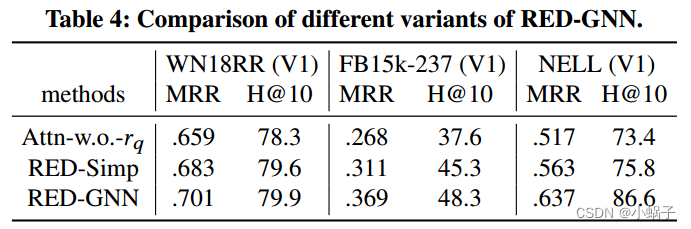
其次,我们将RED-GNN中的算法2替换为算法1中的简单解,即RED-Simp。由于效率问题,不能使用损失函数(6),因为它需要计算许多负三元组的分数。因此,我们使用一个负样本的保证金排名损失,如在GraIL[38]中。如表4所示,RED-Simp的性能弱于RED-GNN,因为其多类对数损失优于负采样的损失函数[22,32,55]。RED-Simp在表1中仍然优于GraIL,因为rdigraps是更好的推理结构。RED-Simp的运行时间如图2(a)和2(b)所示。算法1比算法2昂贵得多,但比GraIL便宜,因为GraIL需要Dijkstra算法来标记实体。
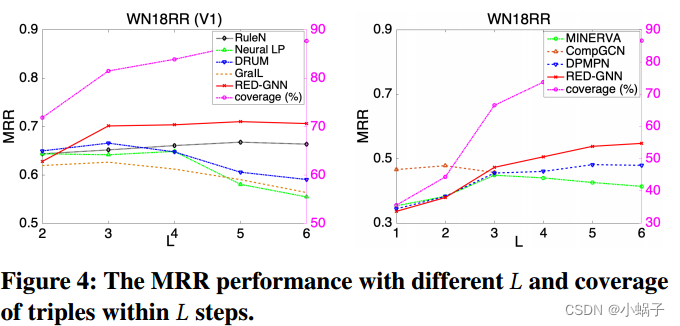
模型的深度。在图4中,我们在左侧𝑦-axis显示了使用不同层或步骤𝐿测试MRR的影响。测试的覆盖率(%)三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎),其中在𝑒𝑎可见从𝑒𝑞在𝐿步骤,也就是说,![]() 。直观地说,当𝐿增加时,将覆盖更多的三元组,𝑒𝑞和𝑒𝑎之间的路径或子图将包含更丰富的信息,但将更难学习。如图所示,当𝐿≥4时,DRUM、Neural LP和MINERVA的性能下降。当𝐿> 3时CompGCN会耗尽内存,并且使用𝐿=3也很难捕获复杂的结构。当𝐿太小,例如𝐿≤2时,RED-GNN的性能较差,主要是由于这种小的r-有向图中编码的信息有限。REDGNN在𝐿≥3时达到最佳性能,此时r-有向图可以包含更丰富的信息,并且可以通过(3)有效地学习到用于推理的重要信息。由于计算成本随着𝐿的增加而显著增加,因此我们对𝐿∈{3,4,5}进行了调整,以在实践中平衡效率和有效性。
。直观地说,当𝐿增加时,将覆盖更多的三元组,𝑒𝑞和𝑒𝑎之间的路径或子图将包含更丰富的信息,但将更难学习。如图所示,当𝐿≥4时,DRUM、Neural LP和MINERVA的性能下降。当𝐿> 3时CompGCN会耗尽内存,并且使用𝐿=3也很难捕获复杂的结构。当𝐿太小,例如𝐿≤2时,RED-GNN的性能较差,主要是由于这种小的r-有向图中编码的信息有限。REDGNN在𝐿≥3时达到最佳性能,此时r-有向图可以包含更丰富的信息,并且可以通过(3)有效地学习到用于推理的重要信息。由于计算成本随着𝐿的增加而显著增加,因此我们对𝐿∈{3,4,5}进行了调整,以在实践中平衡效率和有效性。
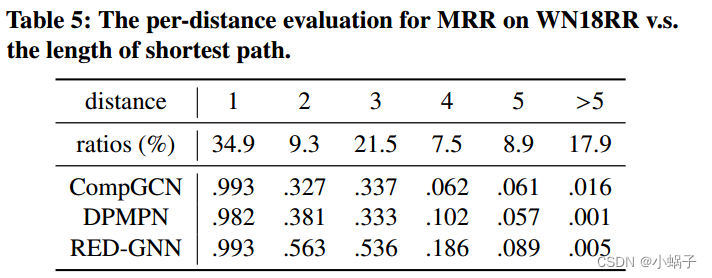
Per-distance性能。注意,给定一个具有𝐿层的r-有向图,两个节点之间不能通过𝐿跳到达的信息不能通过算法2传播。这可能会引起人们对RED-GNN预测能力的担忧,特别是对于𝐿步骤中无法到达的三元组。我们在这里证明这不是一个问题。具体来说,给定一个三元组(𝑒𝑞,𝑟𝑞,𝑒𝑎),我们计算从𝑒𝑞到𝑒𝑎的最短距离。然后,对不同距离的MRR性能进行分组。我们比较了表5中的CompGCN(𝐿= 2)、DPMPN(𝐿=5)和RED-GNN(𝐿=5)。所有模型在距离较大的三元组上的性能都较差,不能很好地模拟距离较远的三元组。RED-GNN在距离5以内具有最佳的单距离性能。
6.结论
在本文中,我们引入了一种新的关系结构,即r-有向图,作为KG推理的关系路径的广义结构。单独计算每个r-有向图对于推理任务来说是昂贵的(𝑒𝑞,𝑟𝑞,?)。因此,受动态规划解决重叠子问题的启发,我们提出了RED-GNN作为GNN的变体,以有效地构造和学习r-有向图。我们表明RED-GNN在具有感应和换能式KG推理基准的KG中都达到了最先进的性能。与其他基于gnn的基线相比,RED-GNN的训练和推理效率很高。此外,RED-GNN还可以学习推理的可解释结构
最后,提出了一种类似于RED-GNN的并行工作NBFNet[57],对查询实体到多个应答实体之间的所有路径进行递归编码。然而, NBFNet使用完全邻接矩阵进行传播,这是非常昂贵的,需要128GB的GPU内存。在未来的工作中,我们可以利用[47]中的修剪技术或[8]中的分布式编程技术,将RED-GNN应用于非常大规模的KG。
相关文章:

Knowledge Graph Reasoning with Relational Digraph
摘要: 知识图推理的目的是从已有的事实中推断出新的事实。基于关系路径的推理方法具有较强的可解释性和可转移性。然而,路径在捕获图中的局部证据方面自然受到限制。在本文中,我们引入了一种新的关系结构,即关系有向图(r-digraph)࿰…...
力扣203:移除链表元素
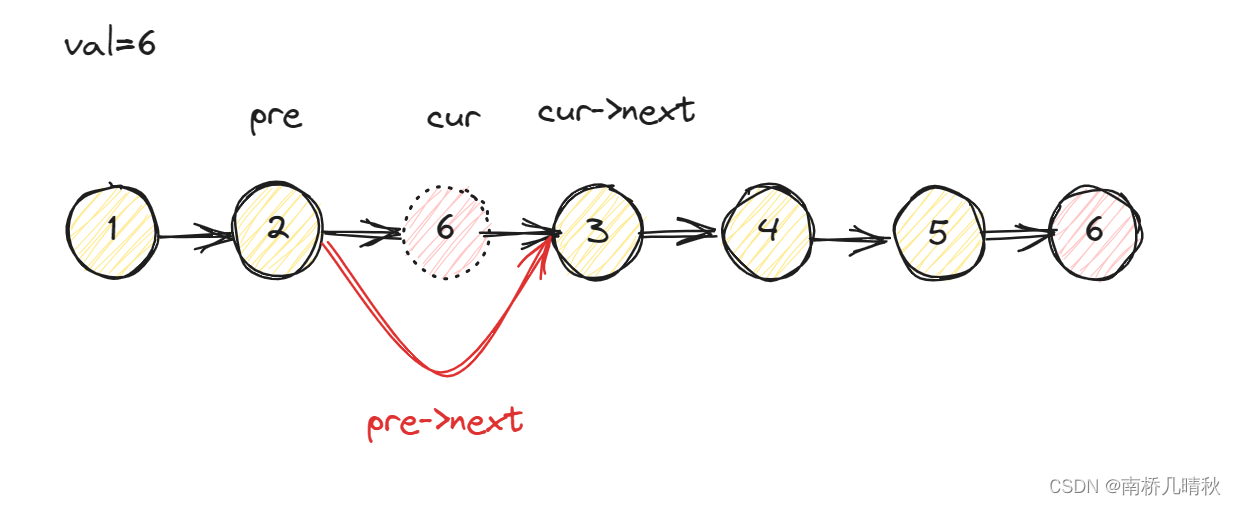
力扣203:移除链表元素 题目描述: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出&a…...

Moto edge s pro手机 WIFI和蓝牙连接不上 解决方法分享
2021年12月入手一台Moto Edge S Pro 12256版,看着性价比很高,越用越垃圾。屏幕显示没有vivo亮丽/APP图标很丑/屏幕上一点点水就失灵/拍照片边缘是模糊的/系统几乎不更新。 以上都可以忍受,但是: 用一年不到,蓝牙不能…...
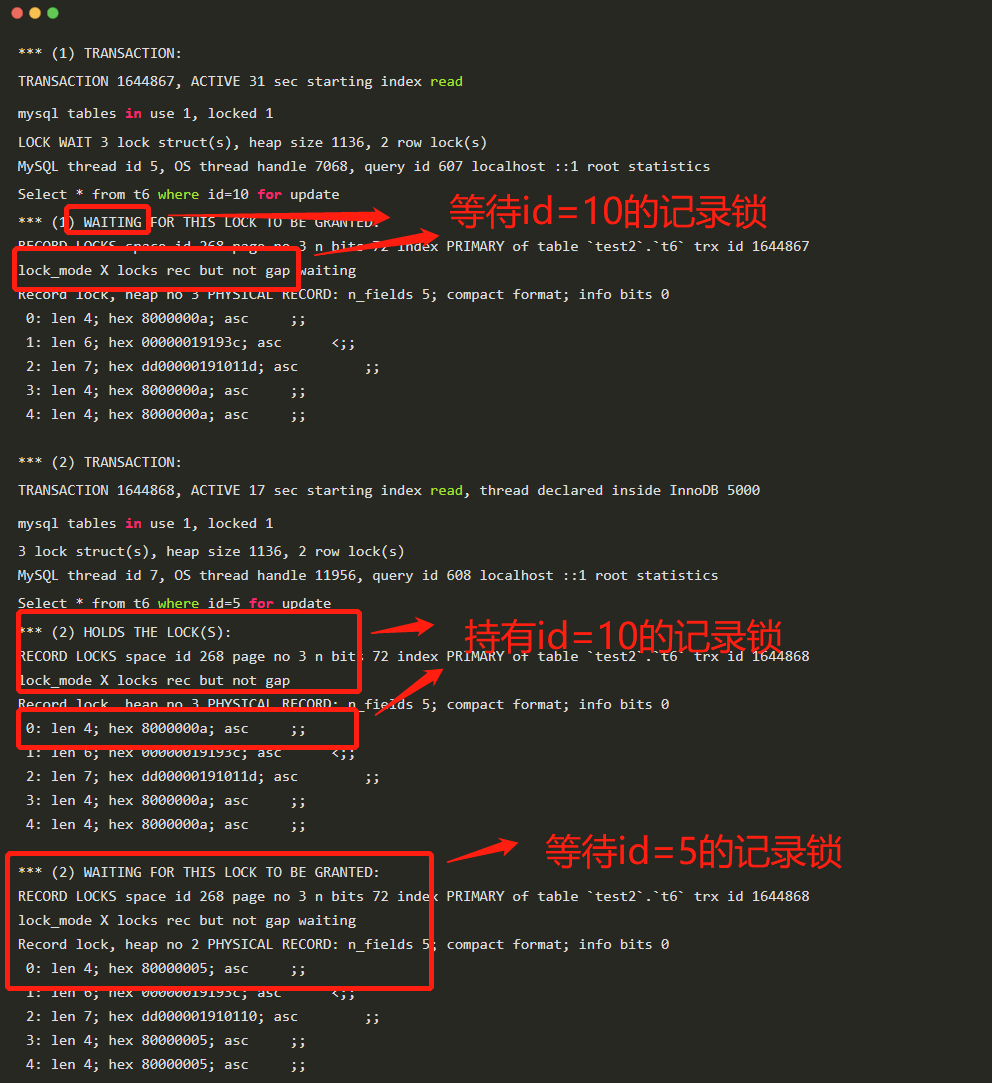
两万字图文详解!InnoDB锁专题!
前言 本文将跟大家聊聊 InnoDB 的锁。本文比较长,包括一条 SQL 是如何加锁的,一些加锁规则、如何分析和解决死锁问题等内容,建议耐心读完,肯定对大家有帮助的。 为什么需要加锁呢? InnoDB 的七种锁介绍 一条 SQL 是…...

2023湖南省赛
连接 目录 A:开开心心233 B:Square Game C:室温超导 F:necklace I:hard math J:radius K:tourist 补题中,会给出大部分代码 A:开开心心233 签到题 ,无论二分还是解方程还是直接for循环枚举都能直接通过啦 signed main() {ios_base:…...
:基础生成表格)
AISchedule(3):基础生成表格
<!DOCTYPE html> <html> <head><meta charset"utf-8"><title>事件列表</title><!-- 加载样式表 --><style>/* 基础样式 */body {background: linear-gradient(to bottom, #f2f2f2, #e0e0e0);font-family: Helvetica…...

OpenAI 上线新功能力捧 RAG,开发者真的不需要向量数据库了?
近期, OpenAI 的开发者大会迅速成为各大媒体及开发者的热议焦点,有人甚至发出疑问“向量数据库是不是失宠了?” 这并非空穴来风。的确,OpenAI 在现场频频放出大招,宣布推出 GPT-4 Turbo 模型、全新 Assistants API 和一…...
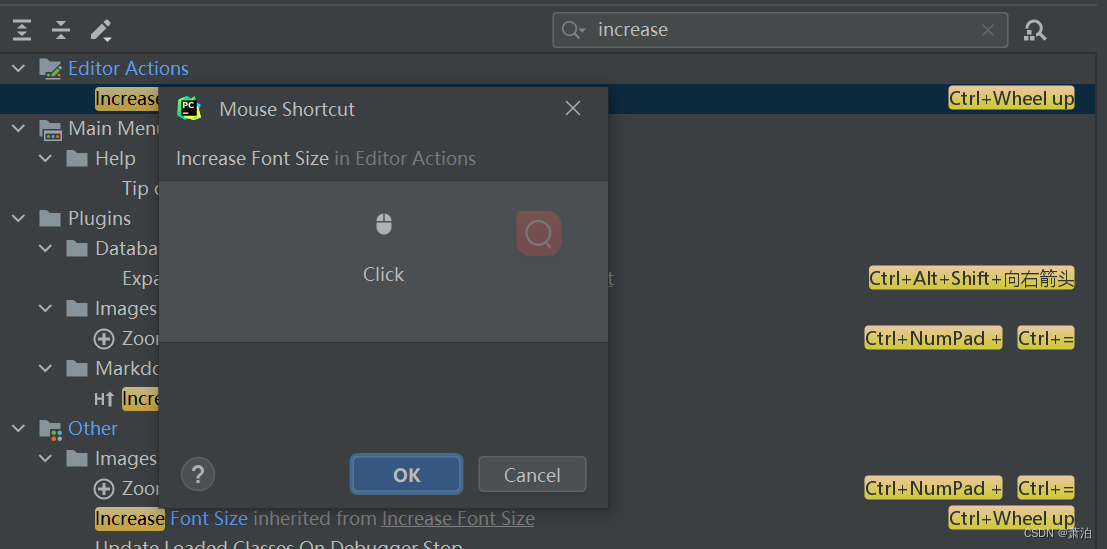
PyCharm鼠标控制字体缩放
File->Settings->Keymap 右边搜索栏输入increase(放大),可以看到下面出现increase Font Size(放大字体尺寸),双击。 双击后出现几个选项,选择Add Mouse Shortcut,会出现一个页面给录入动作。 按住Ctrl同时鼠标向上滚动,该动…...

NI USRP RIO软件无线电
NI USRP RIO软件无线电 NI USRP RIO是SDR游戏规则的改变者,它为无线通信设计人员提供了经济实惠的SDR和前所不高的性能,可帮助开发下一代5G无线通信系统。“USRP RIO”是一个术语,用于描述包含FPGA的USRP软件定义无线电设备,例如…...

kicad源代码研究:symbol properties窗口中为SCH_SYMBOL添加或删除一个sch_field
向grid中添加一个sch_field FIELDS_GRID_TABLE<SCH_FIELD>* m_fields; WX_GRID* m_fieldsGrid; simEnableFieldRow (int) m_fields->size(); m_fields->emplace_back( VECTOR2I( 0, 0 ), simEnableFieldRow, m_symbol, SIM_ENABLE_FIELD ); // notify the grid w…...

httpClient超时时间详解与测试案例
使用httpclient作为http请求的客户端时,我们一般都会设置超时时间,这样就可以避免因为接口长时间无响应或者建立连接耗时比较久导致自己的系统崩溃。通常它里面设置的几个超时时间如下: RequestConfig config RequestConfig.custom().setCo…...

后端接口性能优化分析-数据库优化
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码🔥如果感觉博主的文章还不错的话,请👍三连支持&…...

都很忙,哪里寻找时间?
最近忙不? 多久未联系的朋友发来信息。 我感觉就是一坑。 说忙吧,显得自己很重要,可说不忙吧,又显得没价值。 有事说事,不要上来就说“在不?忙不?有时间不?空不?”等…...
【经验记录】Ubuntu系统安装xxxxx.tar.gz报错ImportError: No module named setuptools
最近在Anaconda环境下需要离线状态(不能联网的情况)下安装一个xxxxx.tar.gz格式的包,将对应格式的包解压后,按照如下命令进行安装 sudo python setup.py build # 编译 sudo python setup.py install # 安装总是报错如下信息&am…...

SDL2 消息循环和事件响应
1.简介 SDL事件可以是用户输入、系统通知或窗口管理事件等。SDL事件可以通过SDL_PollEvent和SDL_WaitEvent函数来获取。在SDL中,事件是通过SDL_Event结构体表示的,其中包含事件类型以及与该类型相关的具体数据。 下面是一些常见的SDL事件类型和相关的事…...
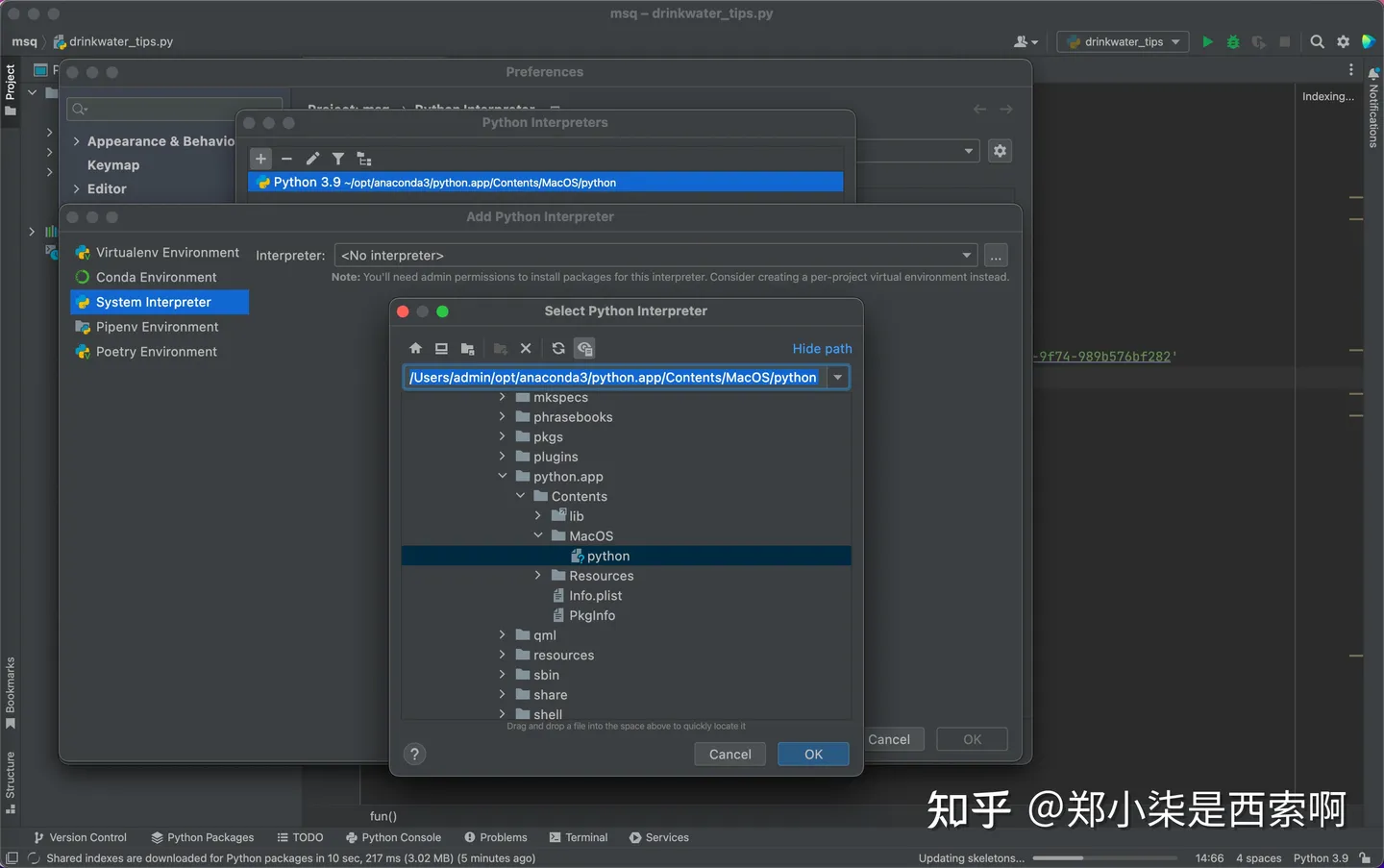
技巧篇:Mac 环境PyCharm 配置 python Anaconda
Mac 中 PyCharm 配置 python Anaconda环境 在 python 开发中我们最常用的IDE就是PyCharm,有关PyCharm的优点这里就不在赘述。在项目开发中我们经常用到许多第三方库,用的最多的命令就是pip install 第三方库名 进行安装。现在你可以使用一个工具来帮你解…...
matplotlib绘图
介绍 在官网上有更多种类的图型的绘制方法 matpoltlib中文官方文档:例子_Matplotlib 中文网 matpoltlib英文官方文档:Examples — Matplotlib 3.8.1 documentation 分类 一、折线图 1、要实现的功能: 2、实例: # 导入包 from…...
QT使用Socket与安卓Socket互发消息
背景:安卓设备通过usb网络共享给Linux,此时安卓设备与linux处于同一网络环境,符合使用socket的条件,linux做客户端,安卓做服务端 1.QT使用Socket (1).在工程文件中加入 QT network (2).导包以及写一些槽函数用做数据传输与状态接收 #ifndef MAINWINDOW_H #define MAINWINDOW…...
Redis05-集群方案
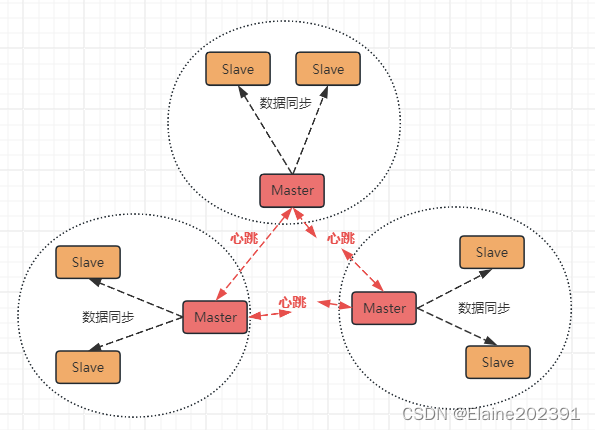
目录 Redis集群方案 主从复制 主从复制的基本原理 主从复制的工作流程 乐观复制 主从复制的优势 哨兵机制 哨兵的关键作用 服务状态监控 哨兵选举Master规则 分片集群 分片集群中的数据读写 数据写入 数据读取 一致性哈希和客户端分片 Redis集群方案 微服务时代…...

故障演练的关键要素及重要性
故障演练是一种有计划的、模拟真实生产环境故障的活动。通过故意引入故障、模拟系统组件失效或模拟其他异常条件,团队可以观察并评估系统在这些情况下的反应。这有助于发现潜在的问题、改进应急响应和提高系统整体的可用性。 一、故障演练的关键要素 计划性…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
