算法与数据结构(一)
一、时间复杂度
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,这个算法流程中,发生了多少常数操作,进而总结出常数操作数量的表达式。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”。
选择排序、冒泡排序的时间复杂度为O(N2)O(N^2)O(N2),额外空间复杂度为O(1)O(1)O(1)
c++实现的选择排序算法:
//创建一个数组int arr[] = {1, 6, 3, 6, 8, 6, 4};//判断数组是否为空或者只有一个数组if (arr == NULL || sizeof(arr) < 2){return;}//开始选择排序for (int i = 0; i < sizeof(arr)/sizeof(arr[0]) - 1; i++){// 暂存最小的数据下标索引int min = i;//从第一个操作数开始筛选for (int j = i + 1; j < sizeof(arr) / sizeof(arr[0]); j++){if (arr[min] > arr[j]){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}}}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){cout << arr[i] << " ";}cout << endl;
冒泡排序:
//创建数组int arr[] = { 2, 3, 5, 1, 3, 4, 5 };//判断数组是否为空或者只有一个数组if (arr == NULL || sizeof(arr) < 2){return;}//开始冒泡排序for (int i = sizeof(arr) / sizeof(arr[0]) - 1; i > 0; i--){for (int j = 0; j < i; j++){if (arr[j] > arr[j+1]){arr[i] = arr[j] ^ arr[i];arr[j] = arr[j] ^ arr[i];arr[i] = arr[j] ^ arr[i];}}}//输出排序后的数组for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){cout << arr[i] << " ";}cout << endl;
以上两种排序算法不管数组内部是什么情况,都需要执行固定的操作,但是插入排序要考虑数组内部的情况,在最好情况下(数组刚好按照想要排序的顺序排列),其时间复杂度为O(N)O(N)O(N),,最差情况下((数组刚好与想要排序的顺序相反)),其时间复杂度为O(N2)O(N^2)O(N2),在时间复杂度的考量上,以最差情况为标准,所以为O(N2)O(N^2)O(N2),其c++实现:
//创建数组int arr[] = { 2, 2, 3, 1, 3, 1, 5, 6 };//如果数组为空或者只有一个数据时,跳过if (arr == NULL || sizeof(arr) < 2){return;}//外侧循环for (int i = 1; i < sizeof(arr)/ sizeof(arr[0]); i++){//内侧循环for (int j = i; j > 0; j--){//如果内测循环指针指向的数据比左侧数据小,则进行交换if (arr[j - 1] > arr[j]){int tem = arr[j];arr[j] = arr[j - 1];arr[j - 1] = tem;}}}//输出排序后的数组for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){cout << arr[i] << " ";}cout << endl;
二、力扣刷题:
有一系列数组,只有一个数字出现了奇数次,其余的数出现了偶数次,求出出现奇数次的数据,要求算法的时间复杂度为O(N):
void test10()
{//创建一系列数组int arr[] = { 2, 2, 3, 1, 3, 1, 5 };int eor = 0;for (int i = 0; i < sizeof(arr)/sizeof(arr[0]); i++){//使用初始变量0逐个异或数组中的每一个元素eor ^= arr[i];}cout << "出现奇数次的数字为: " << eor << endl;
}在异或操作中,0异或0就会出现0的结果,1异或1就等于0,1异或0就等于1。异或操作也可以看成二进制的无进位相加。所以当数组中出现偶数个相同的元素时,其结果会是0,由于异或操作有交换性质,当0异或一个奇数个元素时,其结果就是该数。
有一系列数组,有两个数字出现了奇数次,且这两个奇数次的元素不相等,其余的数出现了偶数次,求出出现奇数次的数据,要求算法的时间复杂度为O(N):
//创建一系列数组int arr[] = { 2, 2, 3, 1, 3, 1, 5, 6 };int eor = 0;int eor1 = 0;for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){//最终得出a异或b的结果eor ^= arr[i];}//提取eor二进制中的最后一个1int RightOne = eor & (~eor + 1);for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){if ((RightOne & arr[i]) == 0){//得出两个奇数次数数字之一eor1 ^= arr[i];}}cout << eor1 << (eor1 ^ eor) << endl;
假设两个出现奇数次的数分别为a,b。这道算法题与之前的算法题有相同之处,但是第一次遍历异或的结果是a异或b。我们只需要知道a或者b再异或一下a异或b的结果就可以得到另一个数字的结果。我们可以这样假设,因为a与b不相等,a异或b的结果也就肯定不为0。在二进制中,a异或b的结果肯定某一位会出现1。假设a异或b的结果为1010。在这里我们只看其中的一位,也就是第二位。a异或b在第二位中出现1,反映到a,b上我们可以知道。a或者b肯定在第二位为1,在这里我们假设a在第二位为1。我们只需要再次迭代一下数组中的元素,可以通过与的操作将第二位上不是1的数进行过滤,如果第二位上是1,我们只需要进行一个异或操作即可,因为除了a之外,其余第二位上是1的数都是偶数,所以最后异或出来的数就是a,再用a异或(a异或b)的结果可以得出b。
相关文章:
)
算法与数据结构(一)
一、时间复杂度 一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。 时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,这个算法流程中,发生了多…...

【Python】元组如何创建?
嗨害大家好鸭!我是小熊猫~ Python 元组 Python 的元组与列表类似, 不同之处在于元组的元素不能修改。 元组使用小括号,列表使用方括号。 元组创建很简单,只需要在括号中添加元素, 并使用逗号隔开即可。 如下实例…...

qt操作文件以及字符串转换
//从文件加载英文属性与中文属性对照表QFile file(":/propertyname.txt");if (file.open(QFile::ReadOnly)) {//QTextStream方法读取速度至少快百分之30#if 0while(!file.atEnd()) {QString line file.readLine();appendName(line);}#elseQTextStream in(&file)…...
)
数组中只出现一次的两个数字(异或法思路)
题目简介 一个数组中只有2个数字只有一个,其他数字都有两个。找出这两个数字。a, b 用HashMap记录就不说了。 这里记录一下用异或的方式解决。 由于异或特性为自己异或自己为0。a^a 0;所以可以异或数组中的所有数字得出 a^b 的结果,其他相同的都消掉…...

python支持的操作系统有哪些
支持python开发环境的系统有Linux、OSX和windows,以及所有主要的操作系统中。 Linux,Linux系统是为编程而设计的,因此在大多数Linux计算机中,都默认安装了Python。编写和维护Linux的人认为会使用这种系统进行编程。要在Linux中运…...

S3C2440开发环境搭建
拿出了之前的S3C2440开发板,然后把移植uboot、移植内核、制作根文件系统、设备树编写驱动等几项再做一遍,这篇文章先记录下环境搭建过程,以及先把现成的uboot、内核、根文件系统下载进去,看看开发板还能不能用,先熟悉一…...

软件测试之测试用例
测试用例 1. 测试用例定义 测试用例又叫做test case,是为某个特殊目标而编制的一组测试输入、执行条件以及预期结果,以便测试某个程序路径或核实是否满足某个特定需求。 2. 编写测试用例的原因 2.1 理清思路,避免遗漏 如果测试的项目大而复杂&#…...

null和undefined的区别有哪些?
null和undefined的区别有哪些?相同点不同点undefinednull总结相同点 1.null和undefined都是js的基本数据类型 2.undefined和null都是假值(falsy),都能作为条件进行判断,所以在绝大多数情况下两者在使用上没有区别 if(undefined)…...

【强烈建议收藏:计算机网络面试专题:HTTP协议、HTTP请求报文和响应报文、HTTP请求报文常用字段、HTTP请求方法、HTTP响应码】
一.知识回顾 之前我们一起学习了HTTP1.0、HTTP1.1、HTTP2.0协议之前的区别、以及URL地址栏中输入网址到页面展示的全过程&&DNS域名解析的过程、HTTP协议基本概念以及通信过程、HTTPS基本概念、SSL加密原理、通信过程、中间人攻击问题、HTTP协议和HTTPS协议区别。接下来…...
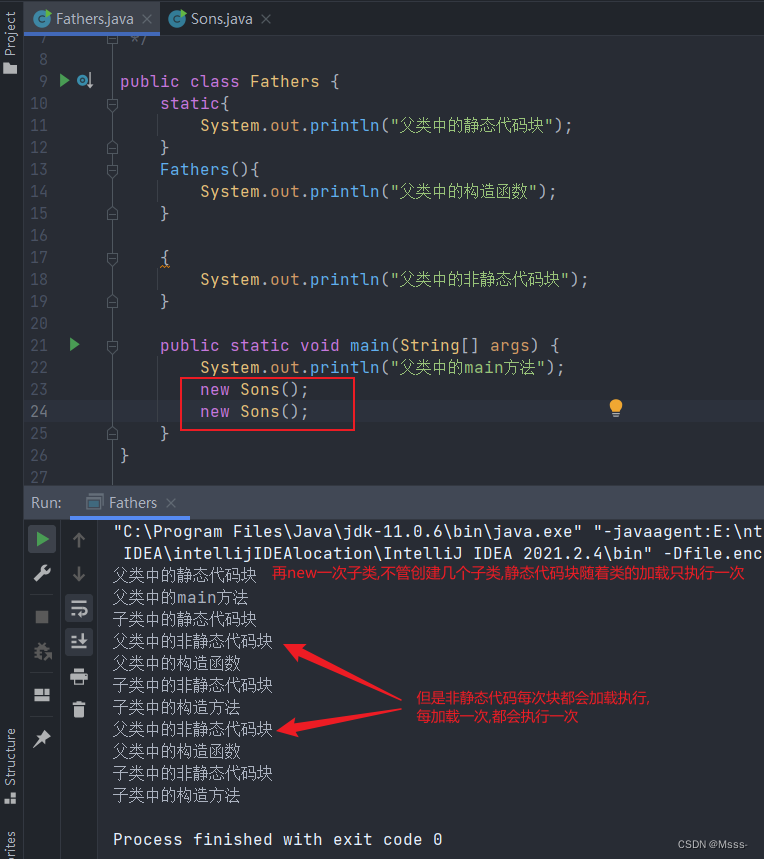
关于Java中的静态块讲解
文章目录类的加载特性与时机类加载的特性类加载的时机static的三个常用地方什么是静态块?特点写法静态块 static怎么用?类的加载特性与时机 在介绍static之前可以先看看类的相关 类加载的特性 在JVM的生命周期里,每个类只会被加载一次。 类加载的原则…...
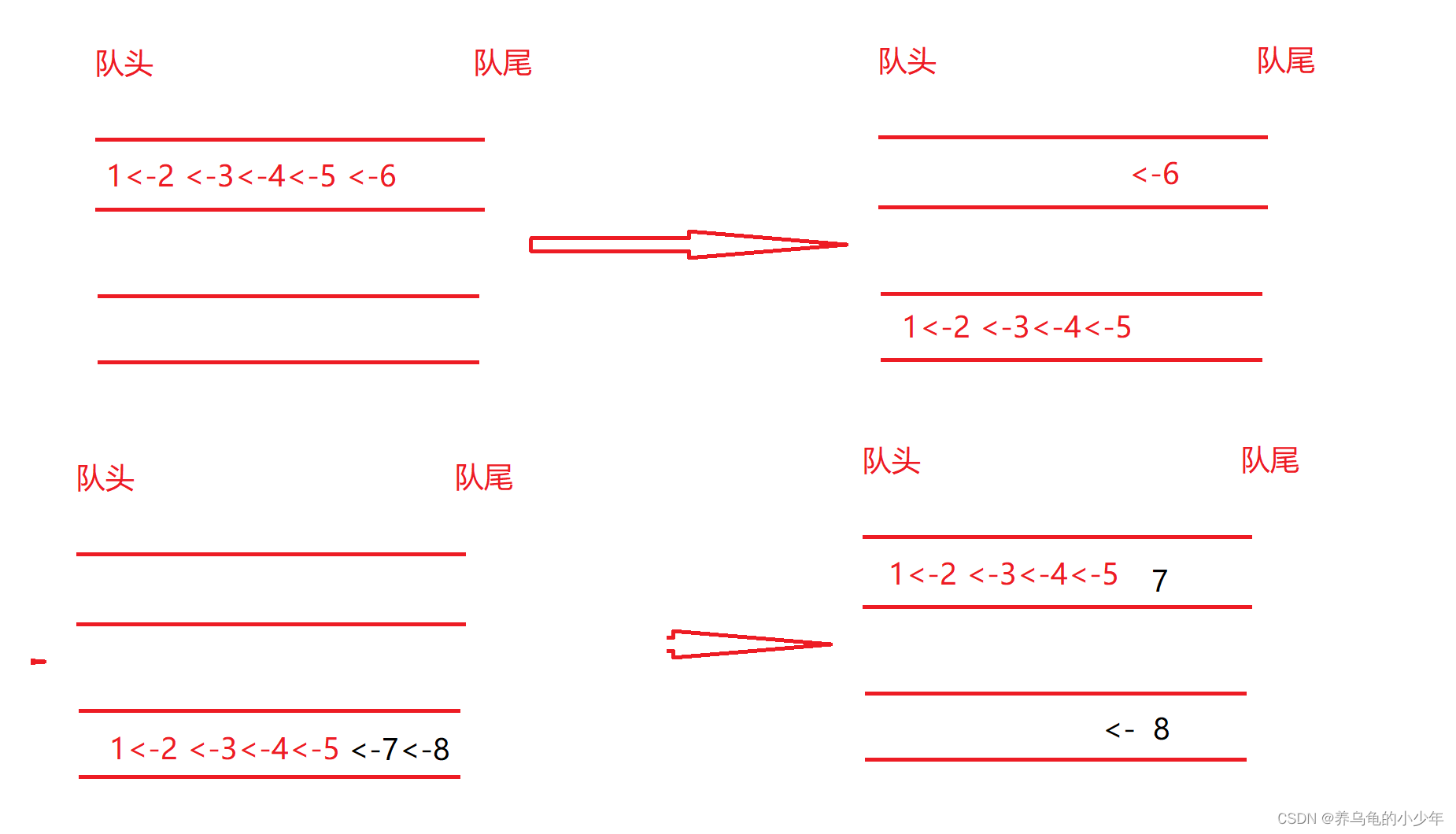
ledcode【用队列实现栈】
目录 题目描述: 解析题目 代码解析 1.封装一个队列 1.2封装带两个队列的结构体 1.3封装指向队列的结构体 1.4入栈函数实现 1.5出栈函数实现 1.6取栈顶数据 1.7判空函数实现 题目描述: 解析题目 这个题我是用c语言写的,所以队列的pu…...

【基础算法】双指针----字符串删减
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Billu靶场黑盒盲打——思路和详解
一、信息收集 1、探测内网主机IP可以使用各种扫描工具比如nmap,我这里用的是自己编写的。 nmap -n 192.168.12.0/24 #扫描IP,发现目标主机 2、先不着急,先收集一波它的端口(无果) nmap -n 192.168.12.136 -p 1-10000…...

【2363. 合并相似的物品】
来源:力扣(LeetCode) 描述: 给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质: items[i] [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,we…...
)
【C++提高编程】C++全栈体系(二十四)
C提高编程 第三章 STL - 常用容器 九、map/ multimap容器 1. map基本概念 简介: map中所有元素都是pairpair中第一个元素为key(键值),起到索引作用,第二个元素为value(实值)所有元素都会根…...
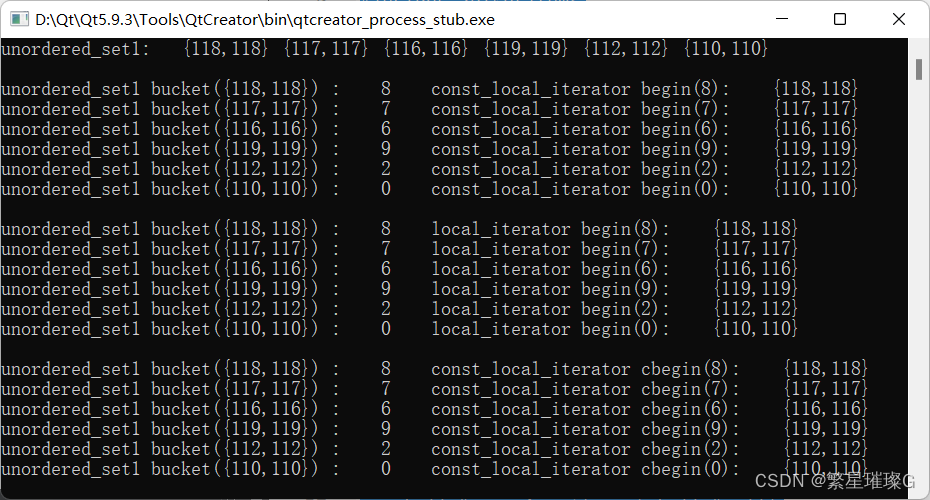
c++11 标准模板(STL)(std::unordered_set)(十一)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

AI/CV大厂笔试LeetCode高频考题之基础核心知识点
AI/CV互联网大厂笔试LeetCode高频考题之基础核心知识点算法复习1、二叉树的遍历2、回溯算法3、二分搜索4、滑动窗口算法题5、经典动态规划6、动态规划答疑篇6.1、总结一下如何找到动态规划的状态转移关系7、编辑距离8、戳气球问题9、最长公共子序列 Longest Common Subsequence…...

华为OD机试题,用 Java 解【静态扫描最优成本】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
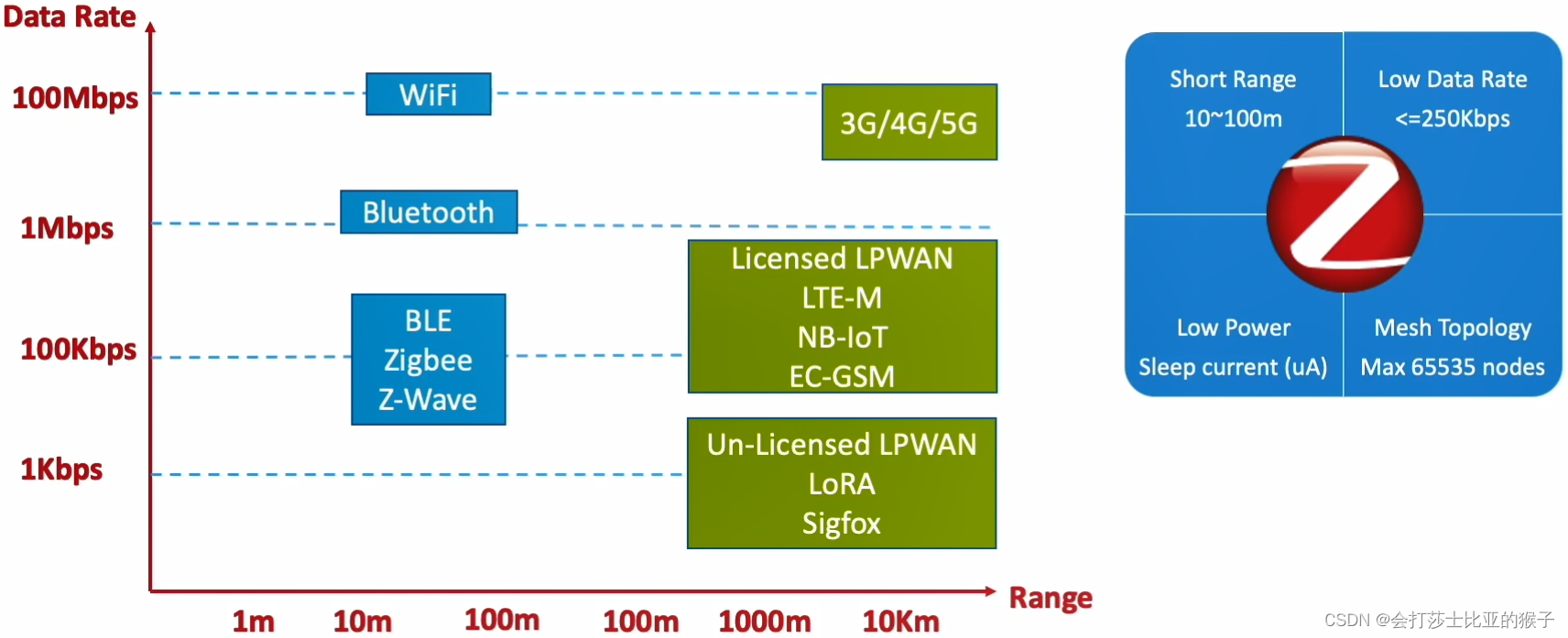
常见无线技术方案介绍
无线技术 无线网络大体有两种:WAN(广域网)、PAN(个人区域网)。 对于LoRa,NB-IoT,2G / 3G / 4G等无线技术,通常传输距离超过1 km,因此它们主要用于广域网(WA…...

收获满满的2022年
收到csdn官方的证书,感谢官方的认可!...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
