【2363. 合并相似的物品】
来源:力扣(LeetCode)
描述:
给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质:
items[i] = [valuei, weighti]其中valuei表示第i件物品的 价值 ,weighti表示第i件物品的 重量 。items中每件物品的价值都是 唯一的 。
请你返回一个二维数组 ret,其中 ret[i] = [valuei, weighti], weighti 是所有价值为 valuei 物品的 重量之和 。
注意: ret 应该按价值 升序 排序后返回。
示例 1:
输入:items1 = [[1,1],[4,5],[3,8]], items2 = [[3,1],[1,5]]
输出:[[1,6],[3,9],[4,5]]
解释:
value = 1 的物品在 items1 中 weight = 1 ,在 items2 中 weight = 5 ,总重量为 1 + 5 = 6 。
value = 3 的物品再 items1 中 weight = 8 ,在 items2 中 weight = 1 ,总重量为 8 + 1 = 9 。
value = 4 的物品在 items1 中 weight = 5 ,总重量为 5 。
所以,我们返回 [[1,6],[3,9],[4,5]] 。
示例 2:
输入:items1 = [[1,1],[3,2],[2,3]], items2 = [[2,1],[3,2],[1,3]]
输出:[[1,4],[2,4],[3,4]]
解释:
value = 1 的物品在 items1 中 weight = 1 ,在 items2 中 weight = 3 ,总重量为 1 + 3 = 4 。
value = 2 的物品在 items1 中 weight = 3 ,在 items2 中 weight = 1 ,总重量为 3 + 1 = 4 。
value = 3 的物品在 items1 中 weight = 2 ,在 items2 中 weight = 2 ,总重量为 2 + 2 = 4 。
所以,我们返回 [[1,4],[2,4],[3,4]] 。
示例 3:
输入:items1 = [[1,3],[2,2]], items2 = [[7,1],[2,2],[1,4]]
输出:[[1,7],[2,4],[7,1]]
解释:
value = 1 的物品在 items1 中 weight = 3 ,在 items2 中 weight = 4 ,总重量为 3 + 4 = 7 。
value = 2 的物品在 items1 中 weight = 2 ,在 items2 中 weight = 2 ,总重量为 2 + 2 = 4 。
value = 7 的物品在 items2 中 weight = 1 ,总重量为 1 。
所以,我们返回 [[1,7],[2,4],[7,1]] 。
提示:
- 1 <= items1.length, items2.length <= 1000
- items1[i].length == items2[i].length == 2
- 1 <= valuei, weighti <= 1000
- items1 中每个 valuei 都是 唯一的 。
- items2 中每个 valuei 都是 唯一的
方法:哈希表
思路与算法
我们建立一个哈希表,其键值表示物品价值,其值为对应价值物品的重量之和。依次遍历 items1 和 items2 中的每一项物品,同时更新哈希表。最后,我们取出哈希表中的每一个键值对放入数组,对数组按照 value 值排序即可。
有些语言可以在维护键值对的同时,对键值对按照「键」进行排序,比如 C++ 中的 std::map,这样我们可以省略掉最后对数组的排序过程。
代码:
class Solution {
public:vector<vector<int>> mergeSimilarItems(vector<vector<int>>& items1, vector<vector<int>>& items2) {map<int, int> mp;for (auto &v : items1) {mp[v[0]] += v[1];}for (auto &v : items2) {mp[v[0]] += v[1];}vector<vector<int>> res;for (auto &[k, v] : mp) {res.push_back({k, v});}return res;}
};
执行用时:8 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:16.4 MB, 在所有 C++ 提交中击败了56.10%的用户
复杂度分析
时间复杂度:O((n+m)log(n+m)),其中 n 是 items1 的长度,m 是 items2 的长度。更新哈希表的时间复杂度为 O(n+m),最后排序的时间复杂度为 (n+m)log(n+m),所以总的时间复杂度为 (n+m)log(n+m)。如果使用有序容器(例如 C++ 中的 std::map),其插入和查询的时间复杂度为 O(log(n+m)),故总体时间复杂度仍然是 O((n+m)log(n+m))。
空间复杂度:O(n+m)。哈希表所使用的空间为 O(n+m)。如果使用有序容器(例如 C++ 中的 std::map),其内部实现为红黑树,空间复杂度为 O(n+m)。
author:LeetCode-Solution
相关文章:

【2363. 合并相似的物品】
来源:力扣(LeetCode) 描述: 给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质: items[i] [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,we…...
)
【C++提高编程】C++全栈体系(二十四)
C提高编程 第三章 STL - 常用容器 九、map/ multimap容器 1. map基本概念 简介: map中所有元素都是pairpair中第一个元素为key(键值),起到索引作用,第二个元素为value(实值)所有元素都会根…...
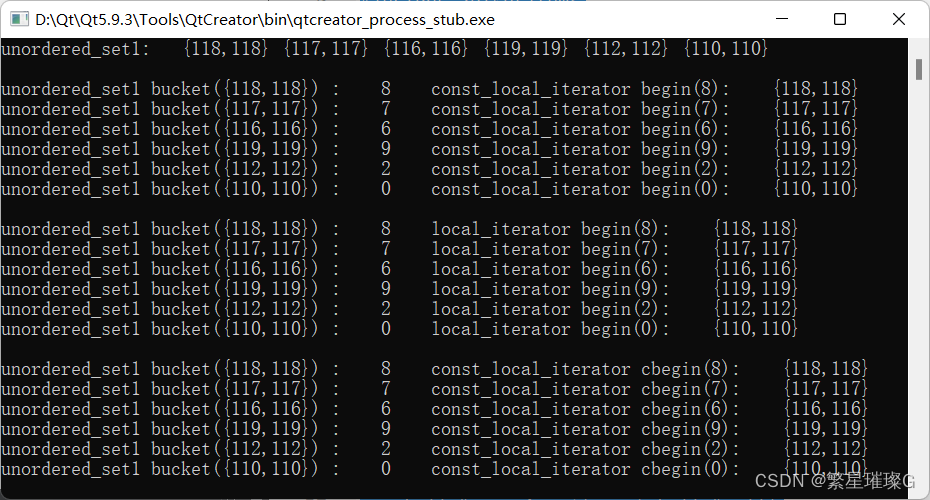
c++11 标准模板(STL)(std::unordered_set)(十一)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

AI/CV大厂笔试LeetCode高频考题之基础核心知识点
AI/CV互联网大厂笔试LeetCode高频考题之基础核心知识点算法复习1、二叉树的遍历2、回溯算法3、二分搜索4、滑动窗口算法题5、经典动态规划6、动态规划答疑篇6.1、总结一下如何找到动态规划的状态转移关系7、编辑距离8、戳气球问题9、最长公共子序列 Longest Common Subsequence…...

华为OD机试题,用 Java 解【静态扫描最优成本】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
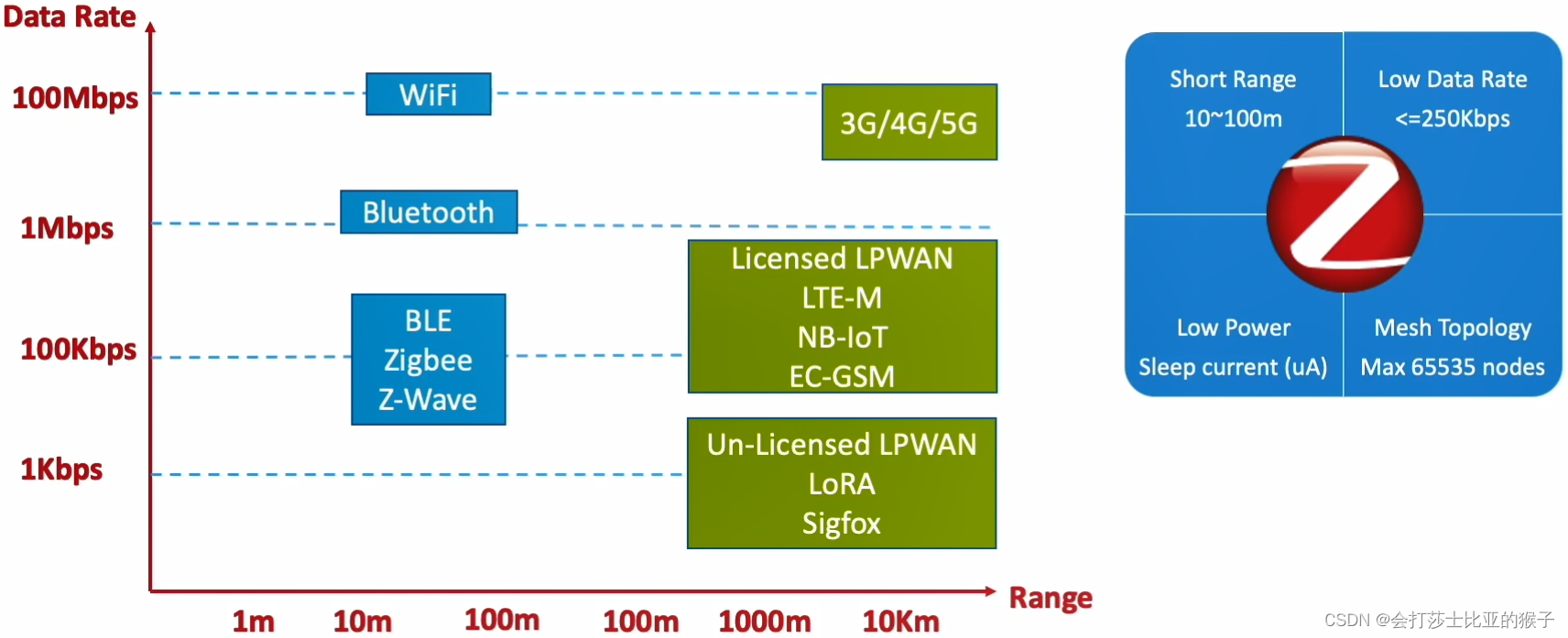
常见无线技术方案介绍
无线技术 无线网络大体有两种:WAN(广域网)、PAN(个人区域网)。 对于LoRa,NB-IoT,2G / 3G / 4G等无线技术,通常传输距离超过1 km,因此它们主要用于广域网(WA…...

收获满满的2022年
收到csdn官方的证书,感谢官方的认可!...

react的生命周期
目录 一、初始化阶段 constructor() static getDerivedStateFromProps() componentWillMount() / UNSAFE_componentWillMount() render(): componentDidMount() 二、运行阶段 componentWillUpdate() / UNSAFE_componentWillUpdate() render() getSnapsh…...

scanpy 单细胞分析API接口使用案例
参考:https://zhuanlan.zhihu.com/p/537206999 https://scanpy.readthedocs.io/en/stable/api.html scanpy python包主要分四个模块: 1)read 读写模块、 https://scanpy.readthedocs.io/en/stable/api.html#reading 2)pp Prepr…...

【Vue3 第二十一章】Teleport组件传送
一、基本使用场景 有时我们可能会遇到这样的场景:一个组件模板的一部分在逻辑上从属于该组件,但从整个应用视图的角度来看,它在 DOM 中应该被渲染在整个 Vue 应用外部的其他地方。 这类场景最常见的例子就是全屏的模态框。理想情况下&#…...

在 Windows Subsystem for Linux (WSL2) 的 Ubuntu 系统上配置 Vulkan 开发环境
在 Windows Subsystem for Linux (WSL2) 的 Ubuntu 系统上配置 Vulkan 开发环境Vulkan Tutorial https://vulkan-tutorial.com/ Development environment - Linux https://vulkan-tutorial.com/Development_environment 1. Vulkan - Cross platform 3D Graphics https://www…...

放苹果HJ61
入门题目 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5&#…...

Windows下,OPC UA移植,open62541移植
OPC通信标准的核心是互通性 (Interoperability) 和标准化 (Standardization) 问题。传统的OPC技术在控制级别很好地解决了硬件设备间的互通性问题,在企业层面的通信标准化是同样需要的。OPC UA之前的访问规范都是基于微软的COM/DCOM技术, 这会给新增层面的通信带来不可根除的…...
【Tomcat与Servlet篇1】认识Tomcat与Maven
目录 一、什么是Tomcat 二、Tomcat的几个重要目录 conf文件编辑 Server.xml logs文件 Webapps目录 三、如何使用Tomcat 但是,如果出现了点击之后进行闪退的情况,那又是怎么回事呢? 原因1:环境变量没有配置 原因2&#…...

C++类和对象:拷贝构造函数和运算符重载
目录 一. 拷贝构造函数 1.1 什么是拷贝构造函数 1.2 编译器默认生成的拷贝构造函数 1.3 拷贝构造函数特性总结 二. 运算符重载 2.1 运算符重载概述 2.2 比较运算符重载(> > < <) 2.2.1 >运算符的重载 2.2.2 运算符的重载 2.…...
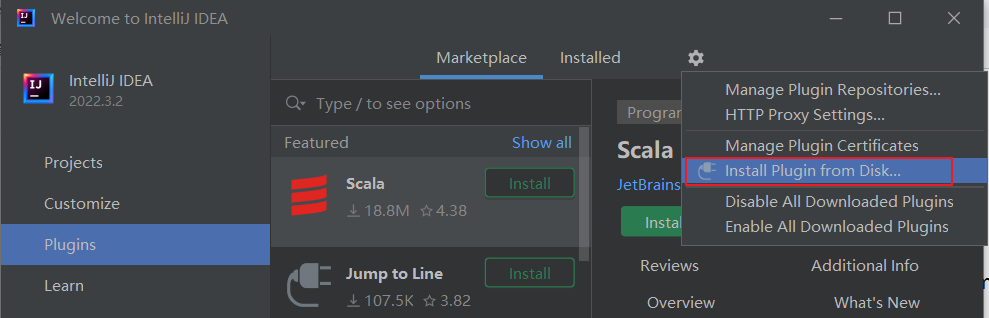
【IntelliJ IDEA】idea plugins搜索不出来,如何找到插件的解决方案
一、背景描述安装好IDEA后,想下载一些插件来使用,因为IDEA非常方便的一点就是插件使用非常的方便,但是经常会发现进入到插件市场无法搜索到插件的情况,这个时候就有点烦人了。那么怎么解决这个问题呢?以下会把我能想到…...

移动端自动化测试(一)appium环境搭建
自动化测试有主要有两个分类,接口自动化和ui自动化,ui自动化呢又分移动端的和web端的,当然还有c/s架构的,这种桌面程序应用的自动化,使用QTP,只不过现在没人做了。 web自动化呢,现在基本上都是…...
5 逻辑回归及Python实现
1 主要思想 分类就是分割数据: 两个条件属性:直线;三个条件属性:平面;更多条件属性:超平面。 使用数据: 5.1,3.5,0 4.9,3,0 4.7,3.2,0 4.6,3.1,0 5,3.6,0 5.4,3.9,0 . . . 6.2,2.9,1 5.1,2.5…...
技术干货 | Modelica建模秘籍之状态变量
在很多领域都有“系统”这个概念,它描述的往往是一些复杂关系的总和。假如我们将系统看做一个黑箱,那么,在系统的作用下,外界的输入有时会产生令人意想不到的输出,“蝴蝶效应”就是其中的典型案例。图1 一只南美洲亚马…...

LeetCode 2574. 左右元素和的差值
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中: answer.length nums.length answer[i] |leftSum[i] - rightSum[i]| 其中: leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
