放苹果HJ61
入门题目
把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5,1)被视为是同一种分法。
示例1
输入:
7 3
输出:
8
1 明确子问题是什么?
m个苹果,n个盘子,他们之间存在的关系要么 m 大于 n , m等于 n,或者 m 小于n ;
所有盘子都放苹果的对立事件是什么?
所有盘子都放苹果的对立事件是至少有一个盘子没有放置苹果。因为在所有的盘子都放置了苹果的情况下,没有盘子是没有放置苹果的,所以所有盘子都放苹果和至少有一个盘子没有放置苹果是互为对立事件。换句话说,如果一个事件发生了,那么另一个事件一定不会发生。
我们定义 dp[ m] [n] 为,m个苹果 ,n个盘子时,一共的分法。就是有两种放苹果的情况,要么n个盘子都放满,要么至少空一个盘子。
dp[ m] [n] = n个盘子都放满的放法 + 至少空一个盘子的方法
n个盘子都放满的方法 : 即要保证所有的盘子中至少都有一个,其他的随便放,所以每个盘子都减去一个苹果,共减去n个苹果即m-n 个,即变成了 m-n 个苹果放在n 个盘子中的放法 ,dp[m-n] [n] 。
至少空一个盘子的方法 :dp[m] [n-1]
保证子问题之间互斥,不重叠。
2 初始值
1 | 1 | 1 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
3 子问题的递推关系
if m< n : # 苹果数量少于盘子数量 100 个苹果放在 5 个盘子的放法数量和 5个苹果放在5个盘子的放法数量一样dp[m][n] = dp[m][m]else m>n :# 所有的盘子都不空的情况 + 存在一个盘子空的情况dp[m][n] = dp[m-n][n] + dp[m][n-1] 4 确定DP数组的计算顺序
递推
defdfs(m,n) :ifm==0 :return1 ; ifn==1 :return1 ; # 只有一个盘子就只有一个放法 ifm<n : returndfs(m,m)# 没有空盘子的放法(每个盘子都至少一个苹果) + 至少一个盘子空着的方法returndfs(m-n, n) +dfs(m, n-1)if__name__=='__main__' :m,n=map(int,(input().split()) )res=dfs(m,n)print(res) 动态规划
# import numpy as np defdfs(m,n) :ifm==0 :return1 ; ifn==1 :return1 ; # 只有一个盘子就只有一个放法 ifm<n : returndfs(m,m)# 没有空盘子的放法 + 至少一个盘子空着的方法returndfs(m-n, n) +dfs(m, n-1)if__name__=='__main__' :m,n=map(int,(input().split()) )# res = dfs(m,n)# print(res)# dp = np.zeros([m+1,n+1],dtype=int)dp= [[0foriinrange(n+1)] foriinrange(m+1)]# 初始化foriinrange(1,n+1): dp[0][i] =1 ; forjinrange(1,m+1): dp[j][1] =1 ; foriinrange(1,m+1) :forjinrange(1,n+1) : # 如果苹果数量少于盘子ifi<j : dp[i][j] =dp[i][j-1]else :# dp[i][j] 即每个状态# dp[i][j] =dp[i-j][j] +dp[i][j-1]print(dp[m][n]) 相关文章:

放苹果HJ61
入门题目 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5&#…...

Windows下,OPC UA移植,open62541移植
OPC通信标准的核心是互通性 (Interoperability) 和标准化 (Standardization) 问题。传统的OPC技术在控制级别很好地解决了硬件设备间的互通性问题,在企业层面的通信标准化是同样需要的。OPC UA之前的访问规范都是基于微软的COM/DCOM技术, 这会给新增层面的通信带来不可根除的…...
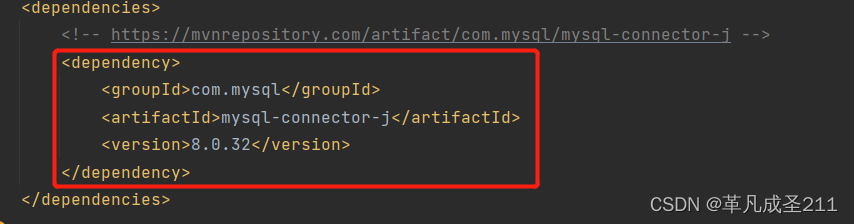
【Tomcat与Servlet篇1】认识Tomcat与Maven
目录 一、什么是Tomcat 二、Tomcat的几个重要目录 conf文件编辑 Server.xml logs文件 Webapps目录 三、如何使用Tomcat 但是,如果出现了点击之后进行闪退的情况,那又是怎么回事呢? 原因1:环境变量没有配置 原因2&#…...

C++类和对象:拷贝构造函数和运算符重载
目录 一. 拷贝构造函数 1.1 什么是拷贝构造函数 1.2 编译器默认生成的拷贝构造函数 1.3 拷贝构造函数特性总结 二. 运算符重载 2.1 运算符重载概述 2.2 比较运算符重载(> > < <) 2.2.1 >运算符的重载 2.2.2 运算符的重载 2.…...
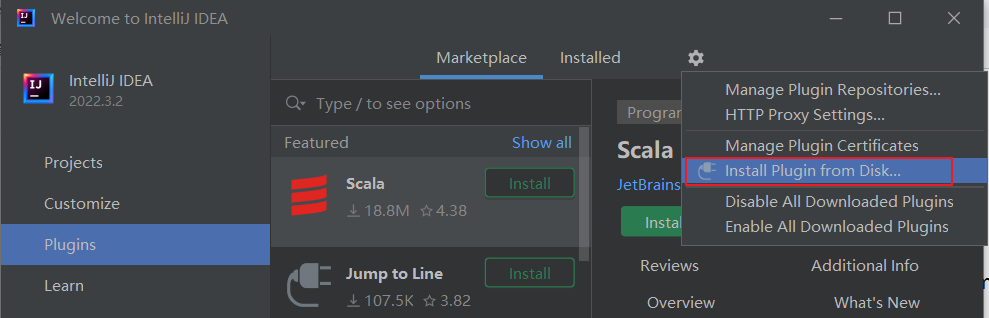
【IntelliJ IDEA】idea plugins搜索不出来,如何找到插件的解决方案
一、背景描述安装好IDEA后,想下载一些插件来使用,因为IDEA非常方便的一点就是插件使用非常的方便,但是经常会发现进入到插件市场无法搜索到插件的情况,这个时候就有点烦人了。那么怎么解决这个问题呢?以下会把我能想到…...

移动端自动化测试(一)appium环境搭建
自动化测试有主要有两个分类,接口自动化和ui自动化,ui自动化呢又分移动端的和web端的,当然还有c/s架构的,这种桌面程序应用的自动化,使用QTP,只不过现在没人做了。 web自动化呢,现在基本上都是…...
5 逻辑回归及Python实现
1 主要思想 分类就是分割数据: 两个条件属性:直线;三个条件属性:平面;更多条件属性:超平面。 使用数据: 5.1,3.5,0 4.9,3,0 4.7,3.2,0 4.6,3.1,0 5,3.6,0 5.4,3.9,0 . . . 6.2,2.9,1 5.1,2.5…...
技术干货 | Modelica建模秘籍之状态变量
在很多领域都有“系统”这个概念,它描述的往往是一些复杂关系的总和。假如我们将系统看做一个黑箱,那么,在系统的作用下,外界的输入有时会产生令人意想不到的输出,“蝴蝶效应”就是其中的典型案例。图1 一只南美洲亚马…...

LeetCode 2574. 左右元素和的差值
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中: answer.length nums.length answer[i] |leftSum[i] - rightSum[i]| 其中: leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不…...

rollup环境配置
VUE2.x源码学习笔记 1. rollup环境配置 首先在VScode中新建文件夹vue_sc,然后终端打开定位到打开的文件夹,输入“npm init -y”初始化配置项,运行成功之后文件夹新增package.json文件 继续在终端运行"npm install babel/preset-env ba…...

二分查找与二分答案、递推与递归、双指针、并查集和单调队列
二分查找与二分答案 文章目录二分查找与二分答案应用总结例题木材加工题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定思路代码递归与递推应用总结[NOIP2003 普及组] 栈题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思…...
如何进行域名购买,获取免费ssl证书,使用springboot绑定ssl证书
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...
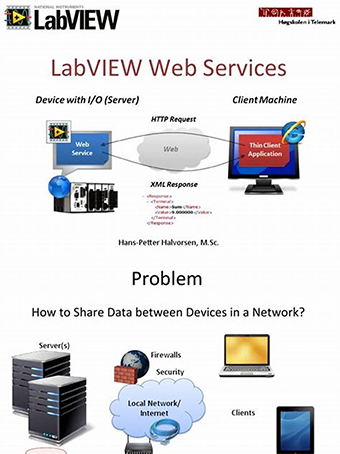
LabVIEW网络服务安全2
LabVIEW网络服务安全2在客户端应用程序中创建签名对请求进行签名要求您具有能够从客户端的编程语言调用的MD5摘要算法以及SHA256加密摘要算法的实现。这两种算法通常都可用于大多数平台。还需要:1. 要使用的HTTP方法的字符串(“GET”、“POST”、“PUT”…...
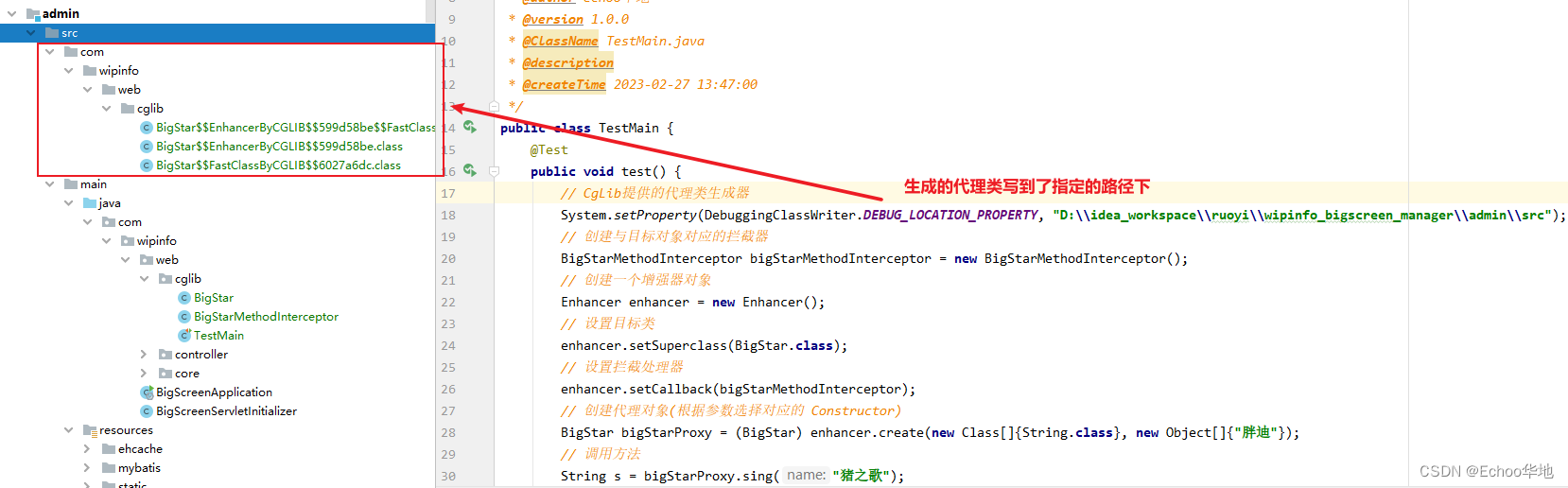
java动态代理
目录儿一、代理模式的作用二、实现代理的方式三、动态代理的实现3.1 jdk动态代理3.2 cglib动态代理一、代理模式的作用 功能增强: 基于某个功能,再增加一些功能。 (比如目标类只负责核心功能,其他附属功能通过代理类完成。代理类的方法名与目…...
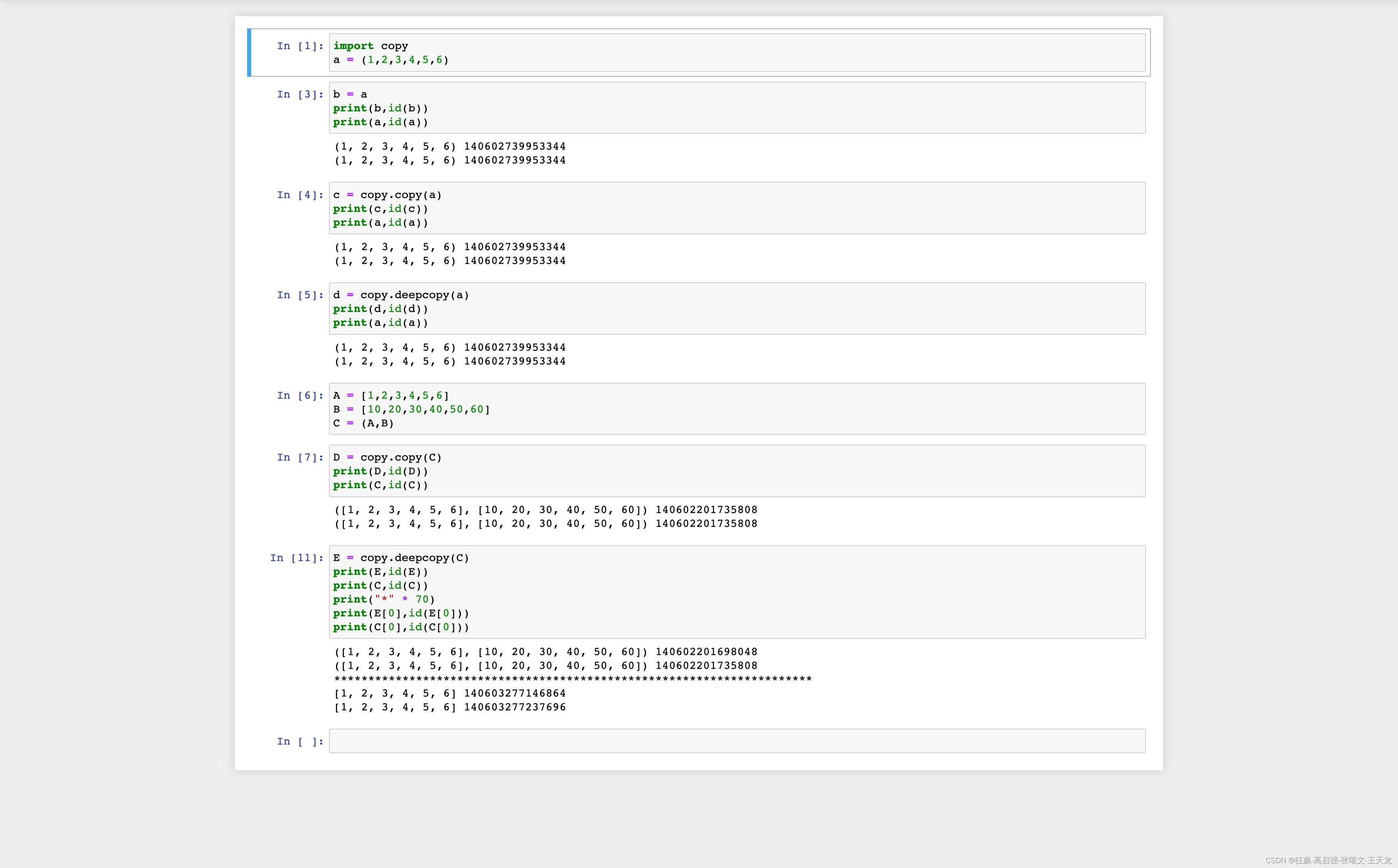
Python 简单可变、复杂可变、简单不可变、复杂不可变类型的copy、deepcopy的行为
copy模块:copy:浅拷贝deepcopy:深拷贝简单可变类型、复杂可变的copy()、deepcopy():简单不可变、复杂不可变类型的copy()、deepcopy():结论:对于简单类型的可变类型copy是深拷贝,改变了该拷贝变…...
QML Item
在QML中所有的可视项目都继承自Item,虽然Item本身没有可视化的外观,但它定义了可视化项目的所有属性。 Item可以作为容器使用: Item{Rectangle{id:retc}Rectangle{id:retc1}Rectangle{id:retc2}Rectangle{id:retc3}} item拥有children属性…...
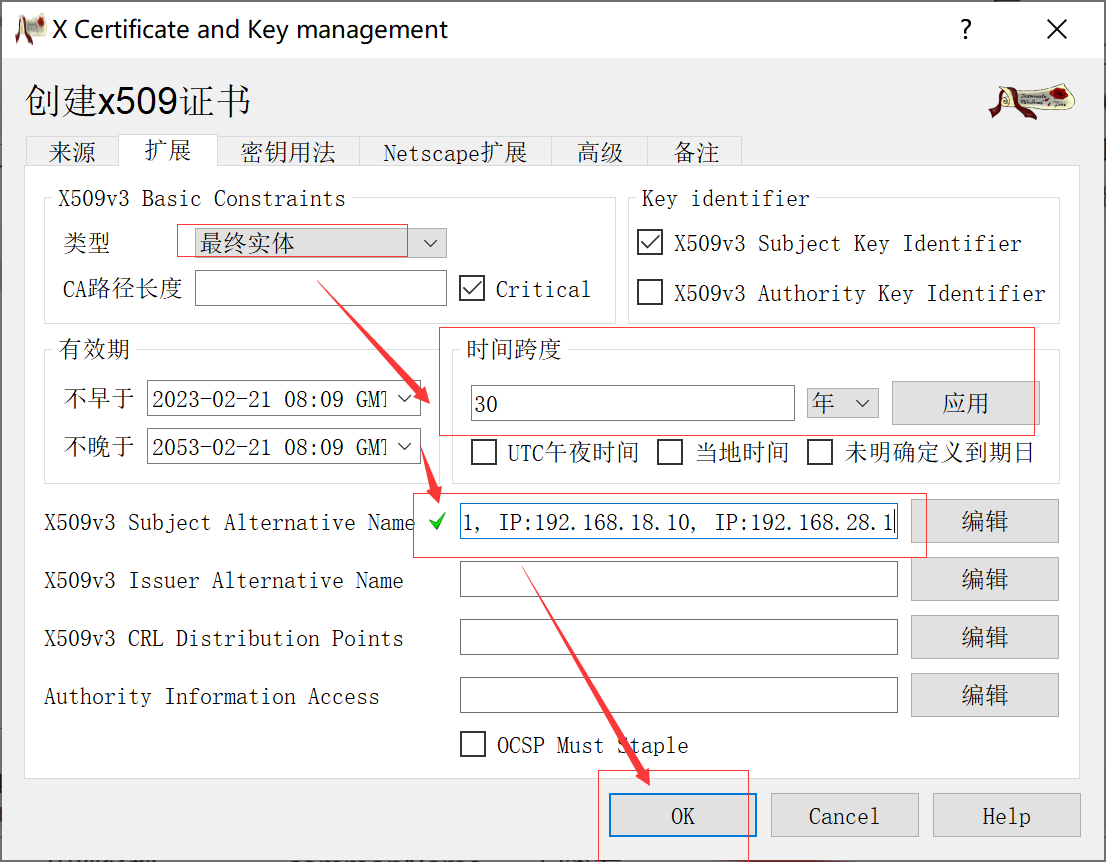
使用xca工具生成自签证书
本文使用 xca 生成自签证书。 概述 之前使用 openssl 生成证书,在 golang 中测试,发现客户端连接失败,经查发现是Subject Alternative Name不支持导致的。因虚拟机 openssl 版本较低,有个功能无法实现,且升级麻烦&…...

Unity IOS 通过命令行导出IPA
新建一个文件然后输入如下内容 #!/usr/bin/env sh /Applications/Unity/Hub/Editor/2020.1.5f1c1/Unity.app/Contents/MacOS/Unity -quit -batchmode -projectPath /Users/zyt/Test -executeMethod Test.BuildEditor.BuildApp cd /Users/zyt/Test/Xcode/unity-xcode xcodebuil…...
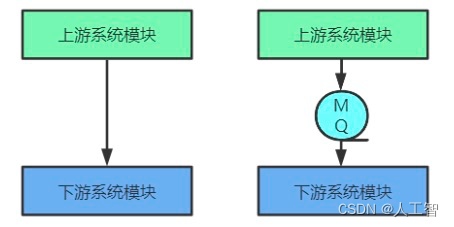
「架构」全链路异步模式
总结自尼恩的全链路异步:网关纯异步化网关层的特点:不需要访问业务数据库只做协议转换和流量转发特点是 IO 密集型,特别适合纯异步的架构,可以极大的节省资源。如何进行网关异步化?使用高性能的通信框架Nettyÿ…...
CleanMyMac4.20最新版新增功能及电脑清理垃圾使用教程
CleanMyMac4.20作为知名的Mac清理工具,仅需一键即可快速而安全地清理系统垃圾,释放磁盘空间,因此一直深受Mac用户的喜爱。在不断更新的版本中,CleanMyMac已经不仅仅满足于只做简单的Mac清理工具,而是为Mac用户提供更多…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
