scanpy 单细胞分析API接口使用案例
参考:https://zhuanlan.zhihu.com/p/537206999
https://scanpy.readthedocs.io/en/stable/api.html
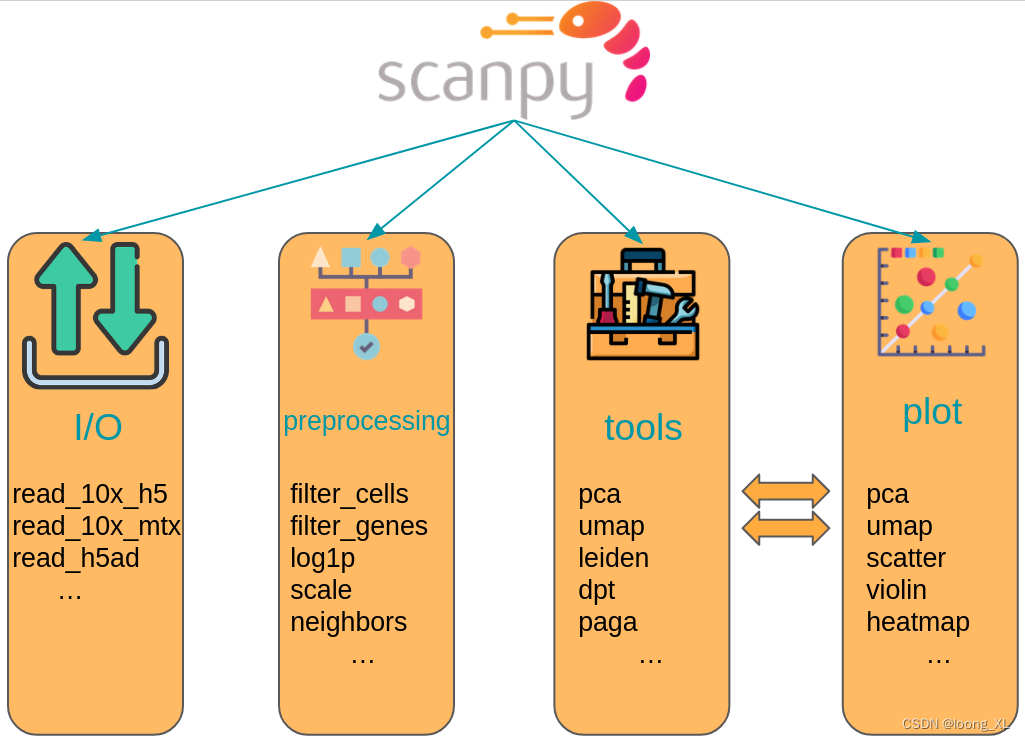
scanpy python包主要分四个模块:
1)read 读写模块、
https://scanpy.readthedocs.io/en/stable/api.html#reading
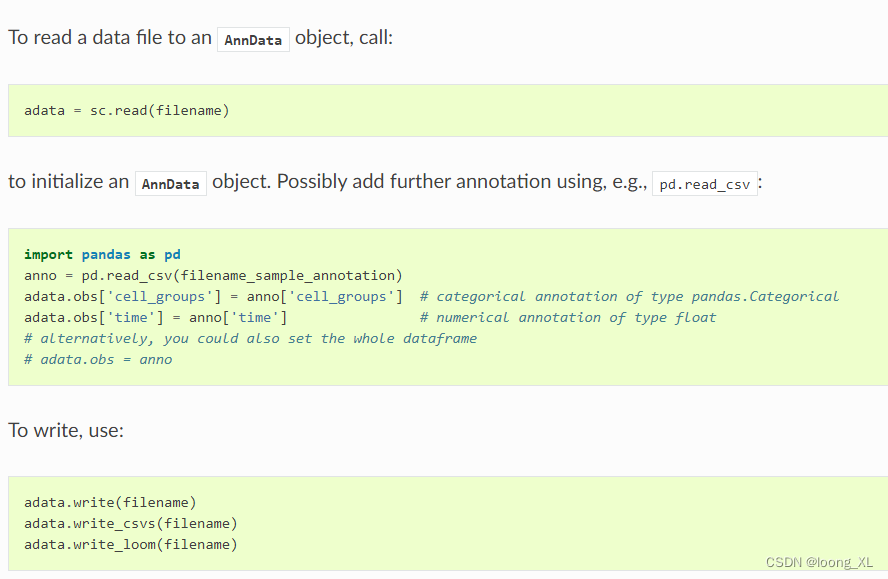
2)pp Preprocessing 预处理模块
https://scanpy.readthedocs.io/en/stable/api.html#module-scanpy.pp

3)tl Tools工具箱模块,包括降维聚类等算法
https://scanpy.readthedocs.io/en/stable/api.html#module-scanpy.tl

3)pl Plotting画图模块
https://scanpy.readthedocs.io/en/stable/api.html#module-scanpy.pl

使用案例
import numpy as np
import pandas as pd
import scanpy as sc## 加载数据
adata = sc.datasets.pbmc3k()
adata.var_names_make_unique()#质量控制
# 查看高表达的前20个基因
sc.pl.highest_expr_genes(adata, n_top=20, save='_pbmc3k.png')#######预处理##############
sc.pp.filter_cells(adata, min_genes=200)
sc.pp.filter_genes(adata, min_cells=3)
adata.var['mt'] = adata.var_names.str.startswith('MT-') # annotate the group of mitochondrial genes as 'mt'
sc.pp.calculate_qc_metrics(adata, qc_vars=['mt'], percent_top=None, log1p=False, inplace=True)#查看
sc.pl.violin(adata, ['n_genes_by_counts', 'total_counts', 'pct_counts_mt'],jitter=0.4, multi_panel=True, save='_pbmc3k.png')adata = adata[adata.obs.n_genes_by_counts < 2500, :]
adata = adata[adata.obs.pct_counts_mt < 5, :]
#总计数归一化、对数化
sc.pp.normalize_total(adata, target_sum=1e4)
sc.pp.log1p(adata)# 识别高度可变的基因
sc.pp.highly_variable_genes(adata, min_mean=0.0125, max_mean=3, min_disp=0.5)
sc.pl.highly_variable_genes(adata, save='_pbmc3k.png')# 保存原始数据
adata.raw = adata# 过滤
adata = adata[:, adata.var.highly_variable]# 将数据缩放到单位方差
sc.pp.regress_out(adata, ['total_counts', 'pct_counts_mt'])
sc.pp.scale(adata, max_value=10)#######降维聚类分析##############sc.tl.pca(adata, svd_solver='arpack')
sc.pl.pca(adata, color='CST3', save='_pbmc3k_CST3.png')
sc.pl.pca_variance_ratio(adata, log=True, save='_pbmc3k_pc.png')
sc.pp.neighbors(adata, n_neighbors=10, n_pcs=40)sc.tl.umap(adata)
sc.pl.umap(adata, color=['CST3', 'NKG7', 'PPBP'], save='_pbmc3k_CST3_NKG7_PPBP.png')sc.tl.leiden(adata)
sc.pl.umap(adata, color=['leiden'], save='_pbmc3k_leiden.png')
相关文章:

scanpy 单细胞分析API接口使用案例
参考:https://zhuanlan.zhihu.com/p/537206999 https://scanpy.readthedocs.io/en/stable/api.html scanpy python包主要分四个模块: 1)read 读写模块、 https://scanpy.readthedocs.io/en/stable/api.html#reading 2)pp Prepr…...

【Vue3 第二十一章】Teleport组件传送
一、基本使用场景 有时我们可能会遇到这样的场景:一个组件模板的一部分在逻辑上从属于该组件,但从整个应用视图的角度来看,它在 DOM 中应该被渲染在整个 Vue 应用外部的其他地方。 这类场景最常见的例子就是全屏的模态框。理想情况下&#…...

在 Windows Subsystem for Linux (WSL2) 的 Ubuntu 系统上配置 Vulkan 开发环境
在 Windows Subsystem for Linux (WSL2) 的 Ubuntu 系统上配置 Vulkan 开发环境Vulkan Tutorial https://vulkan-tutorial.com/ Development environment - Linux https://vulkan-tutorial.com/Development_environment 1. Vulkan - Cross platform 3D Graphics https://www…...

放苹果HJ61
入门题目 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5&#…...

Windows下,OPC UA移植,open62541移植
OPC通信标准的核心是互通性 (Interoperability) 和标准化 (Standardization) 问题。传统的OPC技术在控制级别很好地解决了硬件设备间的互通性问题,在企业层面的通信标准化是同样需要的。OPC UA之前的访问规范都是基于微软的COM/DCOM技术, 这会给新增层面的通信带来不可根除的…...
【Tomcat与Servlet篇1】认识Tomcat与Maven
目录 一、什么是Tomcat 二、Tomcat的几个重要目录 conf文件编辑 Server.xml logs文件 Webapps目录 三、如何使用Tomcat 但是,如果出现了点击之后进行闪退的情况,那又是怎么回事呢? 原因1:环境变量没有配置 原因2&#…...

C++类和对象:拷贝构造函数和运算符重载
目录 一. 拷贝构造函数 1.1 什么是拷贝构造函数 1.2 编译器默认生成的拷贝构造函数 1.3 拷贝构造函数特性总结 二. 运算符重载 2.1 运算符重载概述 2.2 比较运算符重载(> > < <) 2.2.1 >运算符的重载 2.2.2 运算符的重载 2.…...
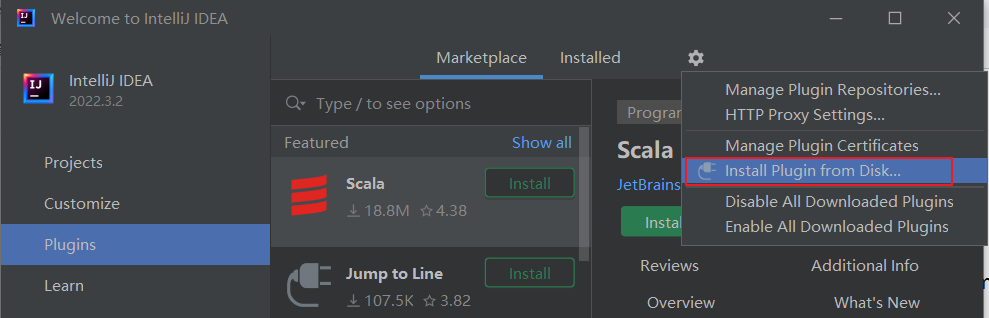
【IntelliJ IDEA】idea plugins搜索不出来,如何找到插件的解决方案
一、背景描述安装好IDEA后,想下载一些插件来使用,因为IDEA非常方便的一点就是插件使用非常的方便,但是经常会发现进入到插件市场无法搜索到插件的情况,这个时候就有点烦人了。那么怎么解决这个问题呢?以下会把我能想到…...

移动端自动化测试(一)appium环境搭建
自动化测试有主要有两个分类,接口自动化和ui自动化,ui自动化呢又分移动端的和web端的,当然还有c/s架构的,这种桌面程序应用的自动化,使用QTP,只不过现在没人做了。 web自动化呢,现在基本上都是…...
5 逻辑回归及Python实现
1 主要思想 分类就是分割数据: 两个条件属性:直线;三个条件属性:平面;更多条件属性:超平面。 使用数据: 5.1,3.5,0 4.9,3,0 4.7,3.2,0 4.6,3.1,0 5,3.6,0 5.4,3.9,0 . . . 6.2,2.9,1 5.1,2.5…...
技术干货 | Modelica建模秘籍之状态变量
在很多领域都有“系统”这个概念,它描述的往往是一些复杂关系的总和。假如我们将系统看做一个黑箱,那么,在系统的作用下,外界的输入有时会产生令人意想不到的输出,“蝴蝶效应”就是其中的典型案例。图1 一只南美洲亚马…...

LeetCode 2574. 左右元素和的差值
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中: answer.length nums.length answer[i] |leftSum[i] - rightSum[i]| 其中: leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不…...

rollup环境配置
VUE2.x源码学习笔记 1. rollup环境配置 首先在VScode中新建文件夹vue_sc,然后终端打开定位到打开的文件夹,输入“npm init -y”初始化配置项,运行成功之后文件夹新增package.json文件 继续在终端运行"npm install babel/preset-env ba…...

二分查找与二分答案、递推与递归、双指针、并查集和单调队列
二分查找与二分答案 文章目录二分查找与二分答案应用总结例题木材加工题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定思路代码递归与递推应用总结[NOIP2003 普及组] 栈题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思…...
如何进行域名购买,获取免费ssl证书,使用springboot绑定ssl证书
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...
LabVIEW网络服务安全2
LabVIEW网络服务安全2在客户端应用程序中创建签名对请求进行签名要求您具有能够从客户端的编程语言调用的MD5摘要算法以及SHA256加密摘要算法的实现。这两种算法通常都可用于大多数平台。还需要:1. 要使用的HTTP方法的字符串(“GET”、“POST”、“PUT”…...
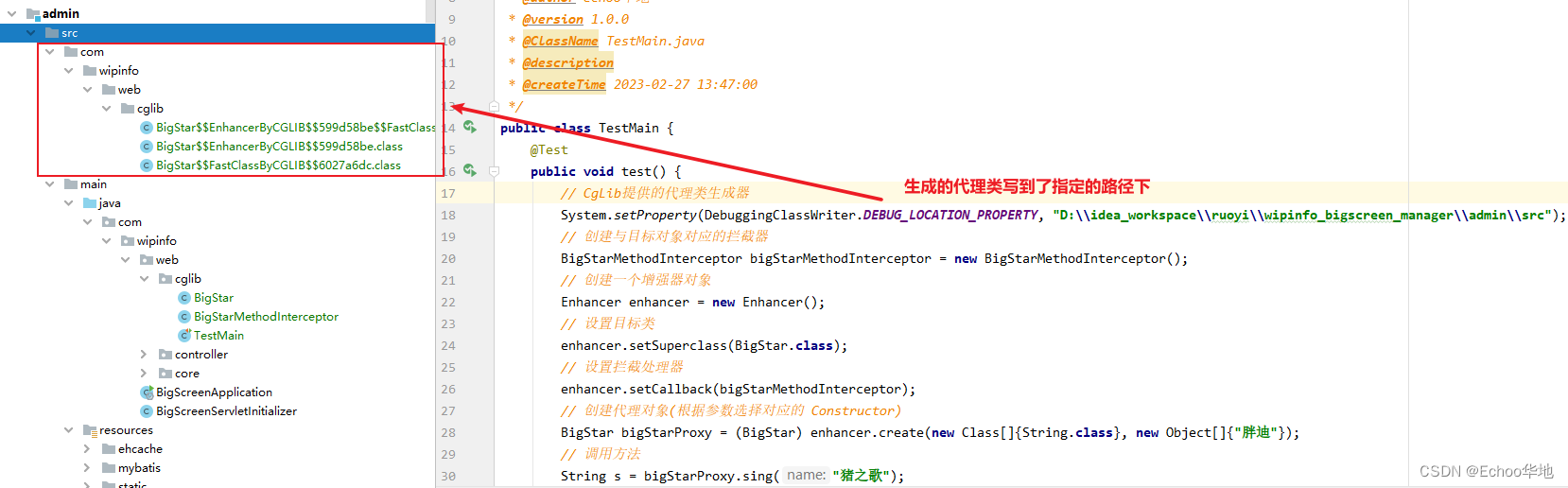
java动态代理
目录儿一、代理模式的作用二、实现代理的方式三、动态代理的实现3.1 jdk动态代理3.2 cglib动态代理一、代理模式的作用 功能增强: 基于某个功能,再增加一些功能。 (比如目标类只负责核心功能,其他附属功能通过代理类完成。代理类的方法名与目…...
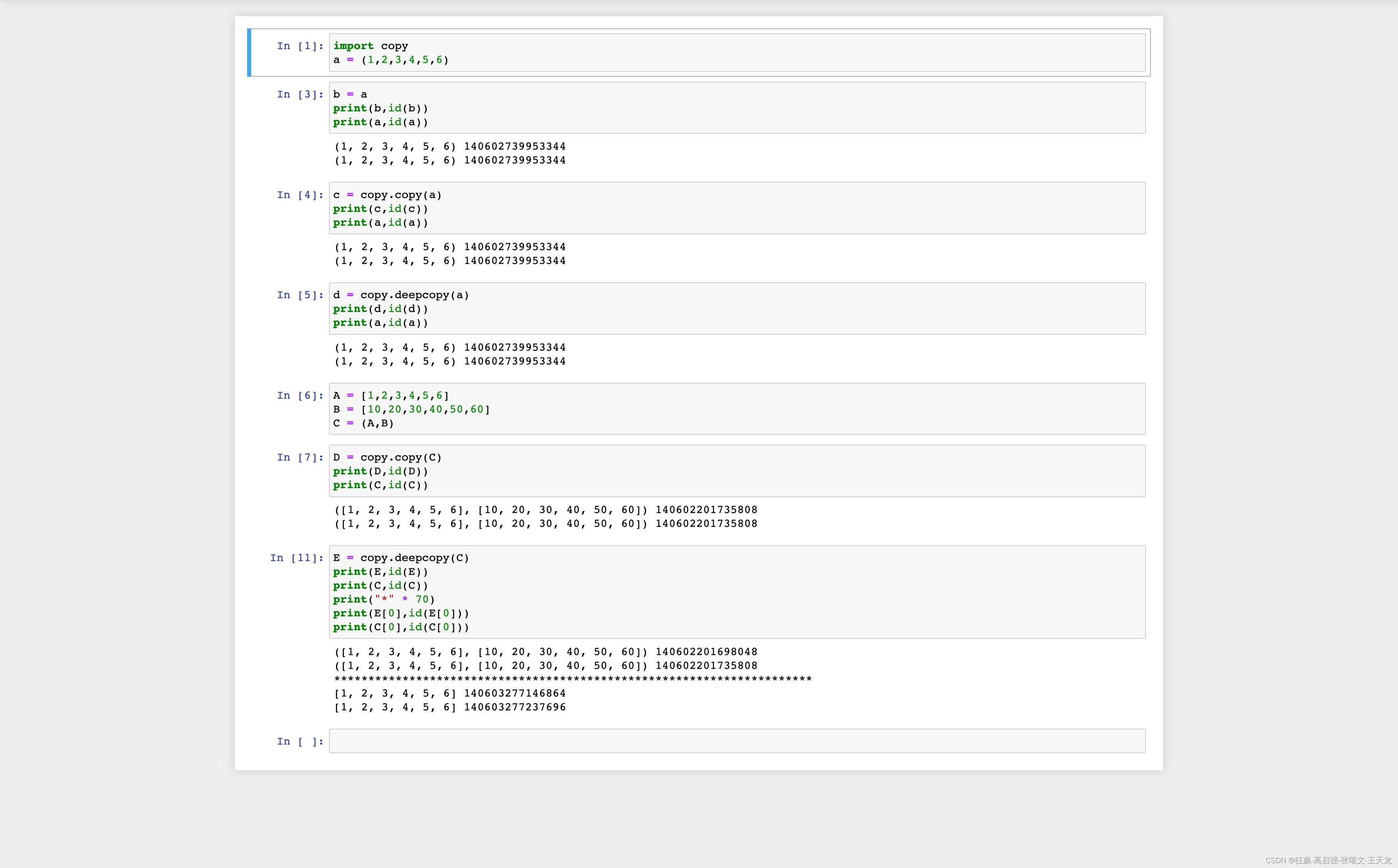
Python 简单可变、复杂可变、简单不可变、复杂不可变类型的copy、deepcopy的行为
copy模块:copy:浅拷贝deepcopy:深拷贝简单可变类型、复杂可变的copy()、deepcopy():简单不可变、复杂不可变类型的copy()、deepcopy():结论:对于简单类型的可变类型copy是深拷贝,改变了该拷贝变…...
QML Item
在QML中所有的可视项目都继承自Item,虽然Item本身没有可视化的外观,但它定义了可视化项目的所有属性。 Item可以作为容器使用: Item{Rectangle{id:retc}Rectangle{id:retc1}Rectangle{id:retc2}Rectangle{id:retc3}} item拥有children属性…...
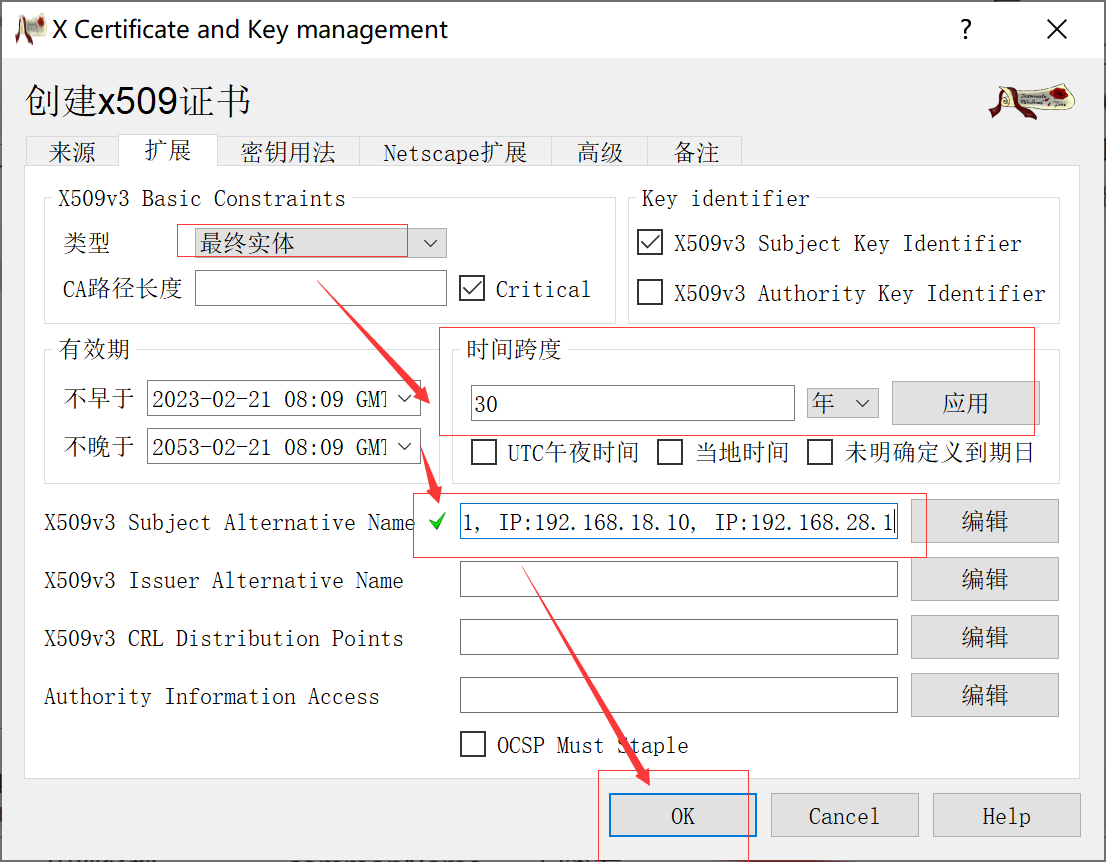
使用xca工具生成自签证书
本文使用 xca 生成自签证书。 概述 之前使用 openssl 生成证书,在 golang 中测试,发现客户端连接失败,经查发现是Subject Alternative Name不支持导致的。因虚拟机 openssl 版本较低,有个功能无法实现,且升级麻烦&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
