python科研绘图:P-P图与Q-Q图
目录
什么是P-P图与Q-Q图
分位数
百分位数
Q-Q图步骤与原理
Shapiro-Wilk检验
绘制Q-Q图
绘制P-P图
什么是P-P图与Q-Q图
P-P图和Q-Q图都是用于检验样本的概率分布是否服从某种理论分布。
P-P图的原理是检验实际累积概率分布与理论累积概率分布是否吻合。若吻合,则散点应围绕在一条直线周围,或者实际累积概率与理论累积概率之差分布在对称于以0为水平轴的带内。
Q-Q图的原理是检验实际分位数与理论分位数是否吻合。若吻合,则散点应围绕在一条直线周围,或者实际分位数与理论分位数之差分布在对称于以0为水平轴的带内。
P-P图和Q-Q图都是用于检验样本的概率分布是否服从某种理论分布。当检验样本的分布为正态分布时,Q-Q图中直线斜率为待检测数据的标准差,截距为均值。
| 特点 | P-P图 | Q-Q图 |
|---|---|---|
| 用途 | 评估累积概率分布函数(CDF)的拟合程度。 | 评估样本分布与理论分布的拟合程度。 |
| 横坐标 | 标准化的观测值(累积概率) | 理论分布的分位数 |
| 纵坐标 | 样本观测值的累积概率 | 理论分布的分位数 |
| 判定标准 | 直观看出CDF的拟合情况,直线越接近对角线越好。 | 点在45度对角线上越接近,拟合越好。 |
| 形状分析 | 对于偏斜、尖峰等分布形状的评估较为直观。 | 主要用于检验是否符合正态分布,对称性等。 |
| 数据量要求 | 对数据量要求不敏感,适用于各种分布的评估。 | 在小样本下效果较好,对数据量要求较高。 |
分位数
分位数, 指的就是连续分布函数中的一个点,这个点对应概率p。若概率0<p<1,随机变量X或它的概率分布的分位数Za,是指满足条件p(X≤Za)=α的实数。
百分位数
百分位数,统计学术语,如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数。可表示为:一组n个观测值按数值大小排列。如,处于p%位置的值称第p百分位数。
Q-Q图步骤与原理
1)将数据升序排列,根据各点在该组数据中的位置,算出累积概率,计算累积概率时(若共n个数),第i个数的累积概率不是i/n,而是用(i-0.5)/n。这可能是为了避免最后一个数的累积概率为1时,反算出的积分上限为正无穷。;
2)根据累积概率,反算出若为标准正态分布,高斯函数的积分上限;

3)积分上限为横坐标,数据点为纵坐标,画出数据分布的QQ图;
4)根据数据的均值与标准差,画出若该组数据为正态分布的QQ图。
P-P图与Q-Q图类似,把分位数换成累积概率。
Shapiro-Wilk检验
Shapiro-Wilk检验是一种用于检验样本数据是否来自正态分布的统计方法。该检验是由Samuel Shapiro和Martin Wilk于1965年提出的。它基于一个假设,即如果样本数据来自正态分布,那么样本数据的顺序统计量应该与对应的理论累积分布函数之间存在线性关系。
Shapiro-Wilk检验的零假设是数据来自正态分布。如果检验结果的p值小于所选定的alpha级别,那么否定假设被拒绝,意味着样本数据不是来自正态分布。反之,如果p值大于选定的alpha级别,则不能拒绝零假设,即数据可能来自正态分布。
绘制Q-Q图
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
plt.rcParams['font.sans-serif'] = ['SimHei'] # 防止中文标签乱码
plt.rcParams['axes.unicode_minus'] = False
# 生成一个示例数据集,这里使用随机数据
np.random.seed(0)
data = np.random.normal(loc=50, scale=5, size=40) # 均值=50,标准差=5
# 正态性检验 - Shapiro-Wilk检验,
# Shapiro-Wilk检验基于W统计量,对数据是否符合正态分布进行评估,适用于各种样本大小
stat, p = stats.shapiro(data)
print("Shapiro-Wilk正态性检验统计量:", stat)
print("Shapiro-Wilk正态性检验p值:", p)
plt.figure(figsize=(6, 6))
# 绘制概率图(probability plot)
# stats.probplot函数通过最小二乘法来估计一组数据的分位数对,并利用线性回归技术求出分位数图上的理论值与实际值的直线方程。
stats.probplot(data, plot=plt, dist='norm', fit=True, rvalue=True)
plt.title('Probability Plot (Q-Q Plot)')
plt.legend()
plt.grid(True)
plt.tight_layout()
# 显示图形
plt.show()Shapiro-Wilk正态性检验统计量: 0.9782676696777344
Shapiro-Wilk正态性检验p值: 0.6254295110702515

绘制P-P图
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
plt.rcParams['font.sans-serif'] = ['SimHei'] # 防止中文标签乱码
plt.rcParams['axes.unicode_minus'] = False
# 生成一个示例数据集,这里使用随机数据
np.random.seed(0)
data = np.random.normal(loc=50, scale=5, size=40) # 均值=50,标准差=5
# 正态性检验 - Shapiro-Wilk检验,
# Shapiro-Wilk检验基于W统计量,对数据是否符合正态分布进行评估,适用于各种样本大小
stat, p = stats.shapiro(data)
print("Shapiro-Wilk正态性检验统计量:", stat)
print("Shapiro-Wilk正态性检验p值:", p)
plt.figure(figsize=(6, 6))
# Create a P-P plot
stats.probplot(data, plot=plt)
# Customize the plot if needed
plt.title('P-P Plot')
plt.xlabel('Theoretical Quantiles')
plt.ylabel('Sample Quantiles')
# Show the plot
plt.show()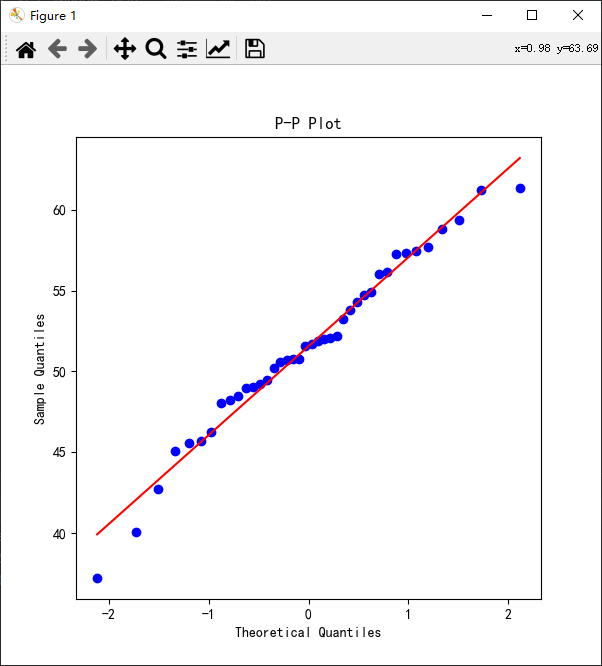
相关文章:

python科研绘图:P-P图与Q-Q图
目录 什么是P-P图与Q-Q图 分位数 百分位数 Q-Q图步骤与原理 Shapiro-Wilk检验 绘制Q-Q图 绘制P-P图 什么是P-P图与Q-Q图 P-P图和Q-Q图都是用于检验样本的概率分布是否服从某种理论分布。 P-P图的原理是检验实际累积概率分布与理论累积概率分布是否吻合。若吻合…...

浅尝:iOS的CoreGraphics和Flutter的Canvas
iOS的CoreGraphic 基本就是创建一个自定义的UIView,然后重写drawRect方法,在此方法里使用UIGraphicsGetCurrentContext()来绘制目标图形和样式 #import <UIKit/UIKit.h>interface MyGraphicView : UIView endimplementation MyGraphicView// Onl…...
网络安全黑客技术自学
前言 一、什么是网络安全 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防…...
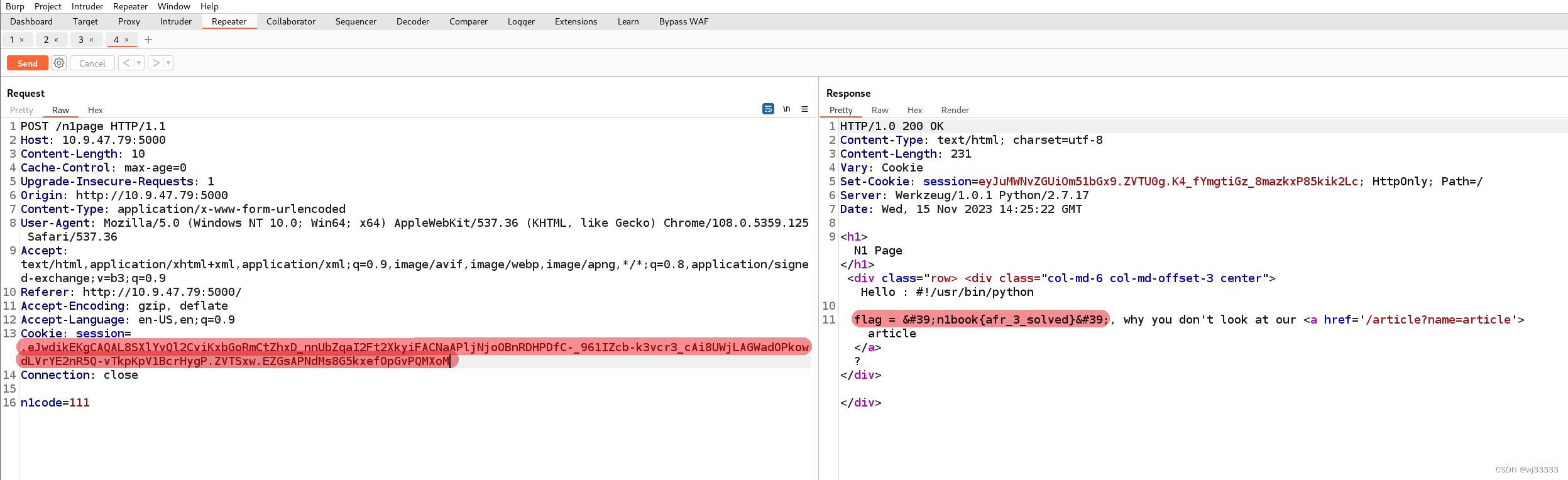
【文件读取/包含】任意文件读取漏洞 afr_3
1.1漏洞描述 漏洞名称任意文件读取漏洞 afr_3漏洞类型文件读取/包含漏洞等级⭐⭐⭐⭐⭐漏洞环境docker攻击方式 1.2漏洞等级 高危 1.3影响版本 暂无 1.4漏洞复现 1.4.1.基础环境 靶场docker工具BurpSuite 1.4.2.环境搭建 1.创建docker-compose.yml文件 version: 3.2 servi…...

第四章:单例模式与final
系列文章目录 文章目录 系列文章目录前言一、单例模式二、final 关键字总结 前言 单例模式与final关键字。 一、单例模式 设计模式是在大量的实践中总结和理论化之后优选的代码结构、编程风格、以及解决问题的思考方式。就像是经典的棋谱,不同的棋局,我…...
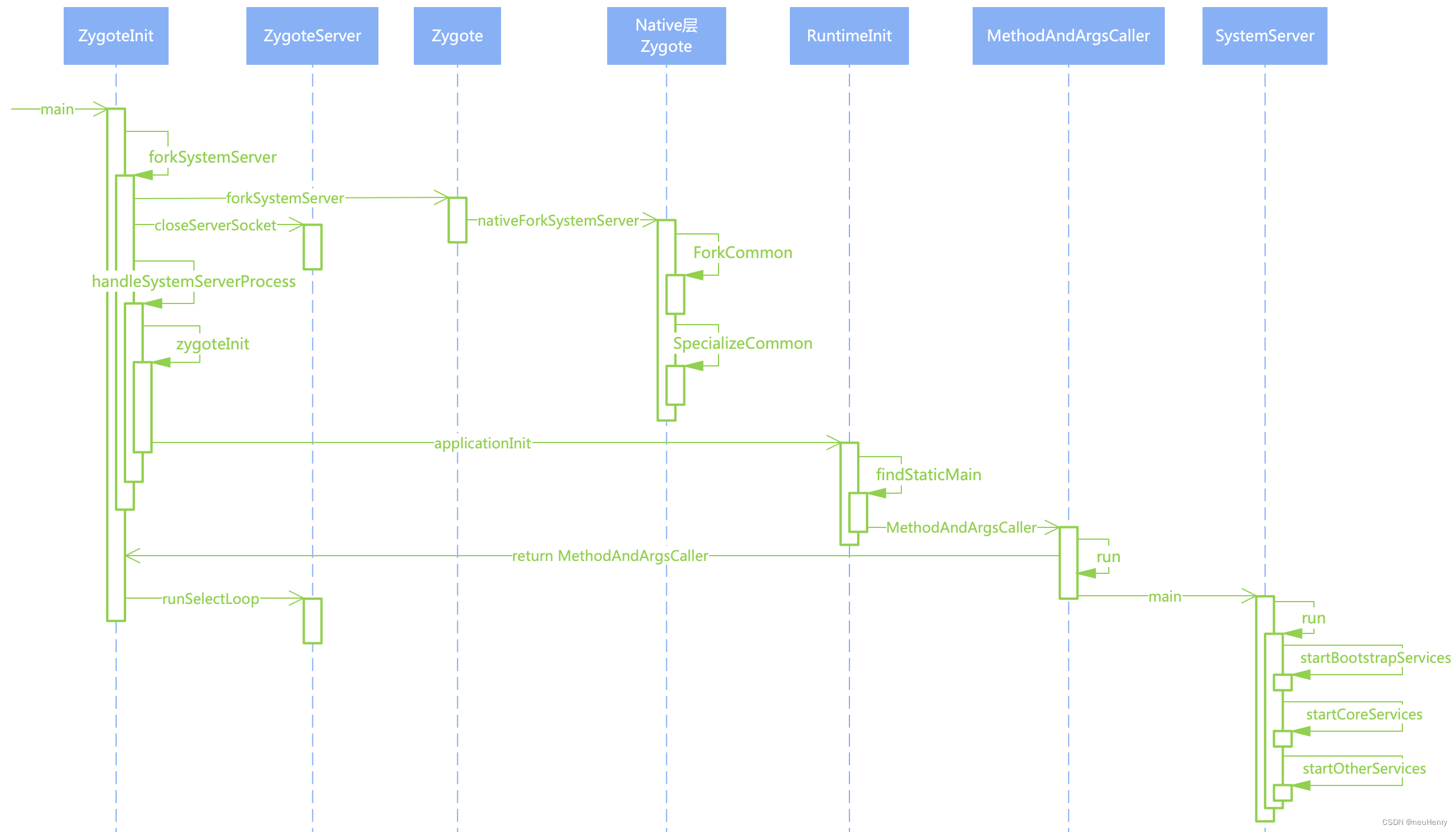
深入Android S(12.0) 探索 Android Framework 之 SystemServer 进程启动详解
深入学习 Android Framework 第三:深入Android S(12.0) 探索 Android Framework 之 SystemServer 进程启动详解 文章目录 深入学习 Android Framework前言一、Android 系统的启动流程1. 流程图2. 启动流程概述 二、源码详解1. 时序图2. 源代码1、ZygoteInit # main…...

搜维尔科技:【软件篇】TechViz是一款专为工程设计的专业级3D可视化软件
在沉浸式房间内深入研究您自己的 3D 数据 沉浸式房间是一个交互式虚拟现实空间,其中每个表面(墙壁、地板和天花板)都充当投影屏幕,创造高度沉浸式的体验。这就像您的 3D 模型有一个窗口,您可以在其中从不同角度走动、…...

android Handler
一、Handler的作用 1、Handler的作用是在andorid中实现线程间的通信。我们常说的说的,子线程处理逻辑,主线程更新UI是上述情况的一个子集。 二、源码分析 1、Handler源码 源码地址:http://androidxref.com/7.1.1_r6/xref/frameworks/base/co…...
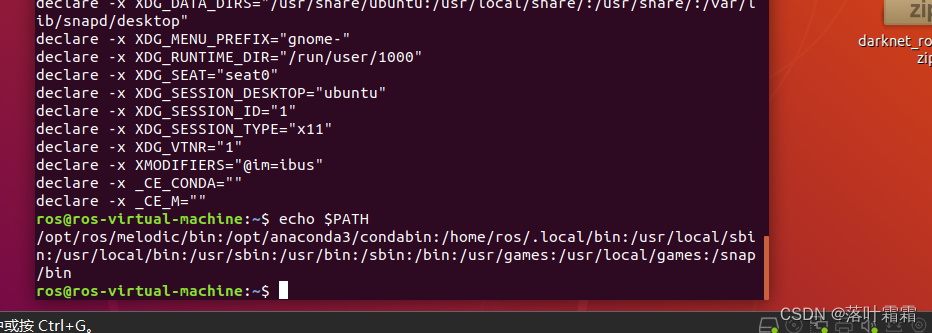
【Ubuntu·系统·的Linux环境变量配置方法最全】
文章目录 概要读取环境变量的方法小技巧 概要 在Linux环境中,配置环境变量是一种常见的操作,用于指定系统或用户环境中可执行程序的搜索路径。 读取环境变量的方法 在Linux中,可以使用以下两个命令来读取环境变量: export 命令…...

Django之模板层
【1】模板之变量 在Django模板中要想使用变量关键是使用点语法。 获取值的语法是:{{ 变量名 }} Python中所有的数据类型包括函数,类等都可以调用 【2】模板之过滤器 过滤器语法 {{ obj | filter_name:param }} obj:变量名字&…...
社区论坛小程序系统源码+自定义设置+活动奖励 自带流量主 带完整的搭建教程
大家好啊,又到了罗峰来给大家分享好用的源码的时间了。今天罗峰要给大家分享的是一款社区论坛小程序系统。社区论坛已经成为人们交流、学习、分享的重要平台。然而,传统的社区论坛往往功能单一、缺乏个性化设置,无法满足用户多样化的需求。而…...

2023亚太杯数学建模C题思路解析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...

acme在同一台服务器上设置多个Ali_key实现自动ssl申请和续期
在同一台服务器上设置多个Ali_key,您可以按照以下步骤进行操作: 首先,确保您已经安装了acme.sh工具。如果没有安装,请先安装acme.sh,您可以使用以下命令安装acme.sh: curl https://get.acme.sh | sh安装完…...

乐观锁与悲观锁
乐观锁 乐观锁是一种并发控制的机制,其核心思想是假设多个事务之间的冲突是不太可能发生的,因此在事务处理之前不会加锁,而是在事务提交的时候再检查是否有冲突。如果发现冲突,就会回滚事务,重新尝试。 实现乐观锁的方…...

【算法】堆排序
算法-堆排序 前置知识 堆(即将更新) 思路 我们现在有一个序列,怎么对它排序? 这是一个非常经典的问题,这里我们使用一个借助数据结构的算法——堆排序解决。 这里有一个序列,要对它升序排序 4 7 3 6 5 …...

51单片机应用从零开始(三)
51单片机应用从零开始(一)-CSDN博客 51单片机应用从零开始(二)-CSDN博客 详解 KEIL C51 软件的使用建立工程-CSDN博客 详解 KEIL C51 软件的使用设置工程编绎与连接程序-CSDN博客 目录 1. 用单片机控制第一个灯亮 2. 认识单片…...

如何在 Nginx Proxy Manager(NPM)上部署静态网站
前言 众所周知,我们在之前介绍过 Nginx Proxy Manager(以下简称 NPM) 这个反向代理的神器,对于一些 Docker 搭建的 Web 项目,NPM 能够很轻松地给他们做反向代理。 然而对于一些静态网站,小伙伴们可能不知道怎么用 NP…...

http的几种方法
http的几种方法在 rfc2616 中进行了定义: https://www.rfc-editor.org/rfc/rfc2616.html#page-51 HEAD方法:HEAD方法和GET方法相同,只不过服务端只返回头,不返回消息体。GET方法:用于获取资源POST方法:用于…...

var、let、const关键字的特性,以及let、const暂时性死区的作用
var、let和const都是JavaScript中的关键字,用于声明变量。 var关键字声明的变量是函数作用域或全局作用域的,它在整个函数或全局范围内都是可用的。var没有块级作用域。 let关键字声明的变量是块级作用域的,它只在包含它的代码块中可用。le…...
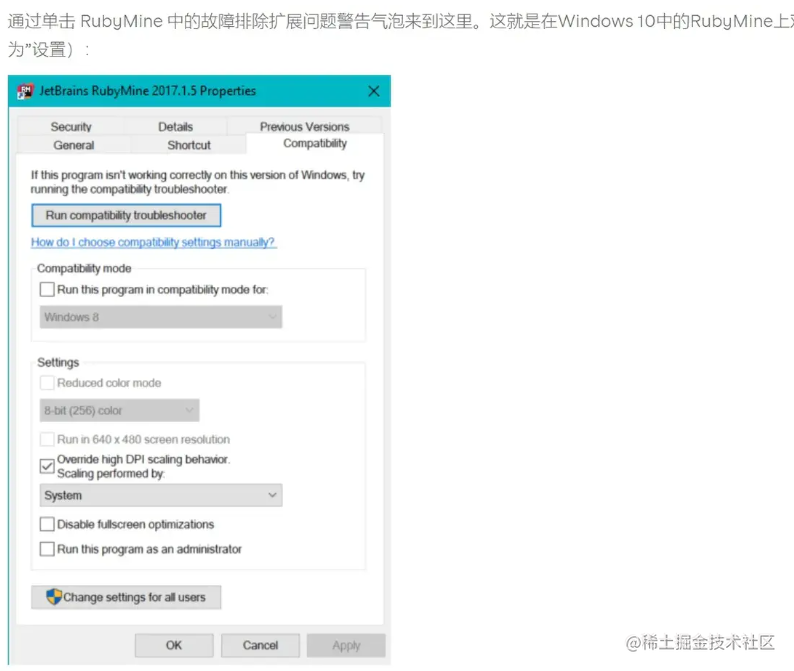
IDEA 高分辨率卡顿优化
VM设置优化 -Dsun.java2d.uiScale.enabledfalse 增加该条设置,关闭高分切换 https://intellij-support.jetbrains.com/hc/en-us/articles/115001260010-Troubleshooting-IDE-scaling-DPI-issues-on-Windowsintellij-support.jetbrains.com/hc/en-us/articles/1…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...
