【洛谷 P2440】木材加工 题解(二分查找+循环)
木材加工
题目背景
要保护环境
题目描述
木材厂有 n n n 根原木,现在想把这些木头切割成 k k k 段长度均为 l l l 的小段木头(木头有可能有剩余)。
当然,我们希望得到的小段木头越长越好,请求出 l l l 的最大值。
木头长度的单位是 cm \text{cm} cm,原木的长度都是正整数,我们要求切割得到的小段木头的长度也是正整数。
例如有两根原木长度分别为 11 11 11 和 21 21 21,要求切割成等长的 6 6 6 段,很明显能切割出来的小段木头长度最长为 5 5 5。
输入格式
第一行是两个正整数 n , k n,k n,k,分别表示原木的数量,需要得到的小段的数量。
接下来 n n n 行,每行一个正整数 L i L_i Li,表示一根原木的长度。
输出格式
仅一行,即 l l l 的最大值。
如果连 1cm \text{1cm} 1cm 长的小段都切不出来,输出 0。
样例 #1
样例输入 #1
3 7
232
124
456
样例输出 #1
114
提示
数据规模与约定
对于 100 % 100\% 100% 的数据,有 1 ≤ n ≤ 1 0 5 1\le n\le 10^5 1≤n≤105, 1 ≤ k ≤ 1 0 8 1\le k\le 10^8 1≤k≤108, 1 ≤ L i ≤ 1 0 8 ( i ∈ [ 1 , n ] ) 1\le L_i\le 10^8(i\in[1,n]) 1≤Li≤108(i∈[1,n])。
思路
函数check()用来判断当前长度x是否满足条件,即根据当前长度可以切割出至少k个长度为x的木棍。在check()函数中,遍历所有木棍,将每个木棍的长度除以x,然后求和,得到切割出的木棍数量。如果切割出的数量大于等于k,则返回true,否则返回false。
在主函数中,定义变量l和r,分别表示长度范围的左右边界。开始时,左边界l为0,右边界r为1e8 + 7。
使用二分查找的思想,当左边界l和右边界r相差1时,即l + 1 < r时,进行循环。每次循环计算中点mid,然后调用check()函数判断mid是否满足条件。
如果mid满足条件,则更新左边界l为mid,因为要找的长度肯定要比mid更大才能满足条件。
如果mid不满足条件,则更新右边界r为mid,因为要找的长度肯定要比mid更小才能满足条件。
最后输出左边界l,即为满足条件的最大长度。
AC代码
#include <iostream>
#define ll long long
using namespace std;const int N = 1e6 + 7;int n, k;
int l[N];bool check(int x) {ll sum = 0;for (int i = 1; i <= n; i++) {sum += l[i] / x;}// cout << x << " " << sum << endl;return sum >= k;
}int main() {cin >> n >> k;for (int i = 1; i <= n; i++) {cin >> l[i];}int l, r;l = 0;r = 1e8 + 7;while (l + 1 < r) {int mid = (l + r) / 2;if (check(mid)) {// 偏短l = mid;} else {// 偏长r = mid;}}cout << l << endl;return 0;
}
相关文章:
)
【洛谷 P2440】木材加工 题解(二分查找+循环)
木材加工 题目背景 要保护环境 题目描述 木材厂有 n n n 根原木,现在想把这些木头切割成 k k k 段长度均为 l l l 的小段木头(木头有可能有剩余)。 当然,我们希望得到的小段木头越长越好,请求出 l l l 的最大…...

反向传播详解BP
误差反向传播(Back-propagation, BP)算法的出现是神经网络发展的重大突破,也是现在众多深度学习训练方法的基础。该方法会计算神经网络中损失函数对各参数的梯度,配合优化方法更新参数,降低损失函数。 BP本来只指损失…...
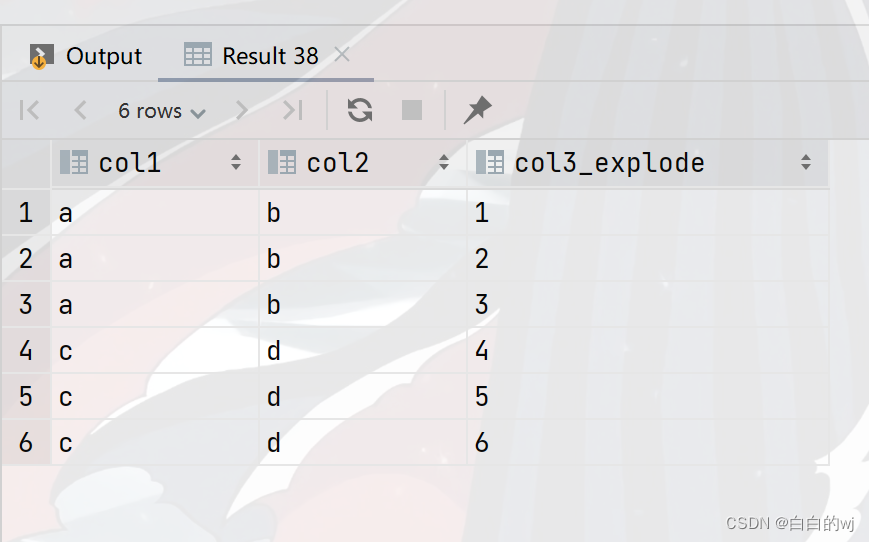
2023.11.16-hive sql高阶函数lateral view,与行转列,列转行
目录 0.lateral view简介 1.行转列 需求1: 需求2: 2.列转行 解题思路: 0.lateral view简介 hive函数 lateral view 主要功能是将原本汇总在一条(行)的数据拆分成多条(行)成虚拟表,再与原表进行笛卡尔积,…...

解决Jetson Xavier NX上Invalid CUDA ‘--device 0‘ requested等问题
解决Jetson Xavier NX上Invalid CUDA --device 0 requested等问题 问题1:AssertionError: Invalid CUDA --device 0 requested, use --device cpu or pass valid CUDA device(s)问题2: “Illegal instruction(cpre dumped)”错误记录python http局域网文…...
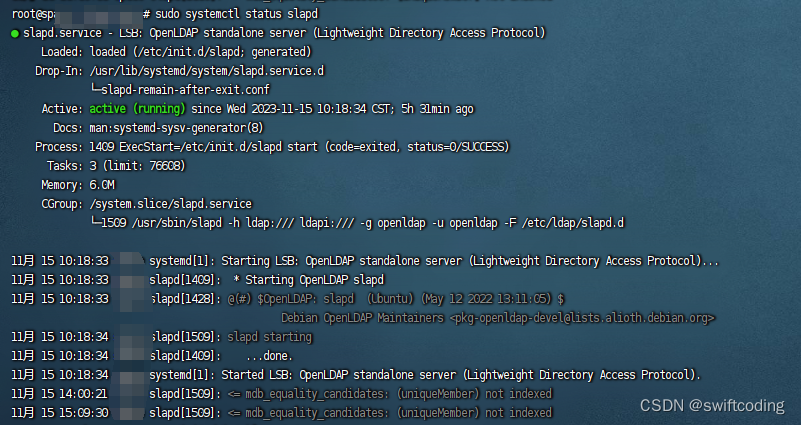
git push 报错 The requested URL returned error: 500
今天gitpush时报错The requested URL returned error: 500 看报错应该是本地和gitlab服务器之间通信的问题,登录gitlab网站查看 登录时报错无法通过ldapadmin认证,ldap服务器连接失败。 首先,登录ldap服务器,查看是否是ldap服务…...

应用软件安全编程--17预防基于 DOM 的 XSS
DOM型XSS从效果上来说也属于反射型XSS,由于形成的原因比较特殊所以进行单独划分。在网站页面中有许多页面的元素,当页面到达浏览器时浏览器会为页面创建一个顶级的Document object 文档对象,接着生成各个子文档对象,每个页面元素对应一个文档…...
【FastCAE源码阅读9】鼠标框选网格、节点的实现
一、VTK的框选支持类vtkInteractorStyleRubberBandPick FastCAE的鼠标事件交互类是PropPickerInteractionStyle,它扩展自vtkInteractorStyleRubberBandPick。vtkInteractorStyleRubberBandPick类可以实现鼠标框选物体,默认情况下按下键盘r键开启框选模式…...

【ArcGIS处理】行政区划与流域区划间转化
【ArcGIS处理】行政区划与流域区划间转化 引言数据准备1、行政区划数据2、流域区划数据 ArcGIS详细处理步骤Step1:统计行政区划下子流域面积1、创建批量处理模型2、添加批量裁剪处理3、添加计算面积 Step2:根据子流域面积占比均化得到各行政区固定值 参考…...
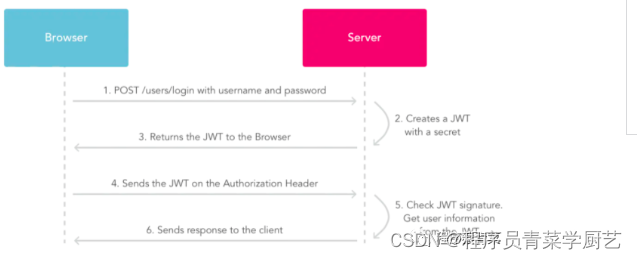
Session、Token、Jwt三种登录方案介绍
新开发一个应用首先要考虑的就是登录怎么去做,登录本身就是判断一下输入的用户名和密码与系统存储的是否一致,但因为Http是无状态协议,用户请求其它接口时是怎么判断该用户已经登录了呢?下面聊一个三种实现方案。 一、传统sessio…...

Linux操作系统使用及C高级编程-D5Linux shell命令(进程管理、用户管理)
进程管理 查看进程ps 其中ps -eif可显示父进程 实时查看进程top 按q退出 树状图显示进程pstree 以父进程,子进程以树状形式展示 发送信号kill kill -l:查看都有哪些信号 9:进程终止 kill不指定信号,默认发送的是15信号SIGT…...

【TDSQL-PG数据库简单介绍】
TDSQL-PG数据库简单介绍 TDSQL-PGTDSQL-PG 设计目标 TDSQL-PG 腾讯 TDSQL-PG 分布式关系型数据库是一款面向海量在线实时分布式事务交易和 MPP 实时数据分析 通用型高性能数据库系统。 面对应用业务产生的不定性数据爆炸需求,不管是高并发的交易还是海量的实时数据…...
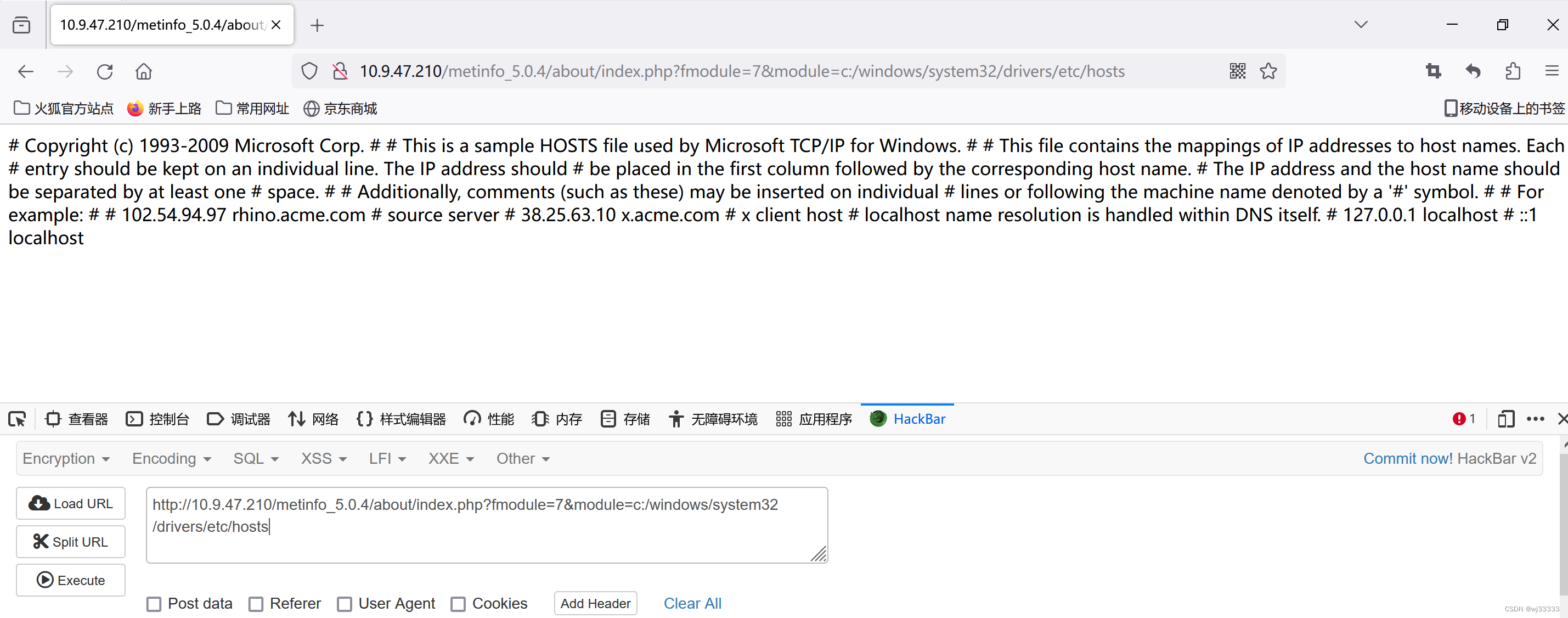
【文件包含】metinfo 5.0.4 文件包含漏洞复现
1.1漏洞描述 漏洞编号————漏洞类型文件包含漏洞等级⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐漏洞环境windows攻击方式 MetInfo 是一套使用PHP 和MySQL 开发的内容管理系统。MetInfo 5.0.4 版本中的 /metinfo_5.0.4/about/index.php?fmodule文件存在任意文件包含漏洞。攻击者可利用漏洞读取网…...
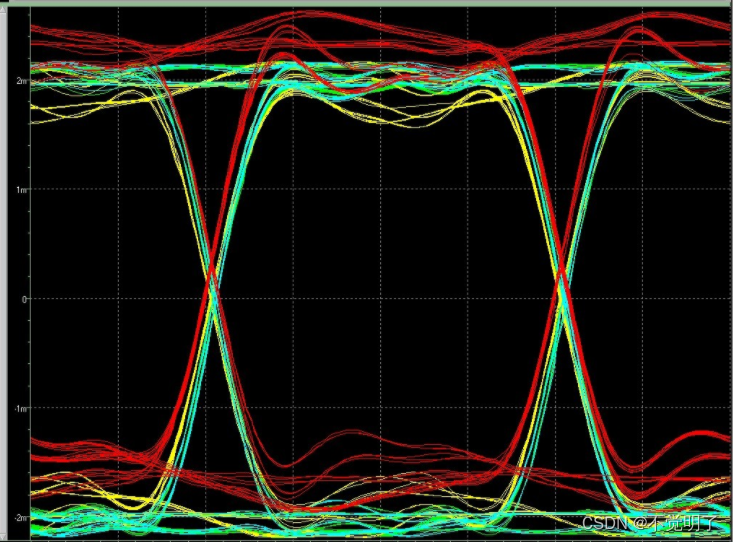
差分信号的末端并联电容到底有什么作用?
差分信号的末端并联电容到底有什么作用? 在现代电子系统中,差分信号是一种常见的信号形式,它们通过两根互补的信号线传输信号,具有较低的噪声和更高的抗干扰能力。然而,当差分信号线长度较长或者遇到复杂的电路环境时&…...

pandas教程:GroupBy Mechanics 分组机制
文章目录 Chapter 10 Data Aggregation and Group Operations(数据汇总和组操作)10.1 GroupBy Mechanics(分组机制)1 Iterating Over Groups(对组进行迭代)2 Selecting a Column or Subset of Columns (选中…...
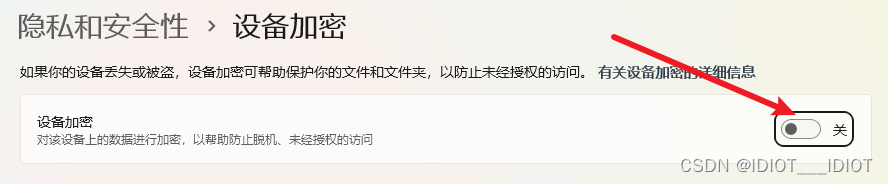
通过右键用WebStorm、Idea打开某个文件夹或者在某一文件夹下右键打开当前文件夹用上述两个应用
通过右键用WebStorm、Idea打开某个文件夹或者在某一文件夹下右键打开当前文件夹用上述两个应用 通过右键点击某个文件夹用Idea打开 首先打开注册表 win R 输入 regedit 然后找到HKEY_CLASSES_ROOT\Directory\shell 然后右键shell 新建一个项名字就叫 Idea 第一步…...

Android 10.0 framework层设置后台运行app进程最大数功能实现
1. 前言 在10.0的定制开发中,在系统中,对于后台运行的app过多的时候,会比较耗内存,导致系统运行有可能会卡顿,所以在系统优化的 过程中,会限制后台app进程运行的数量,来保证系统流畅不影响体验,所以需要分析下系统中关于限制app进程的相关源码来实现 功能 2.framewo…...
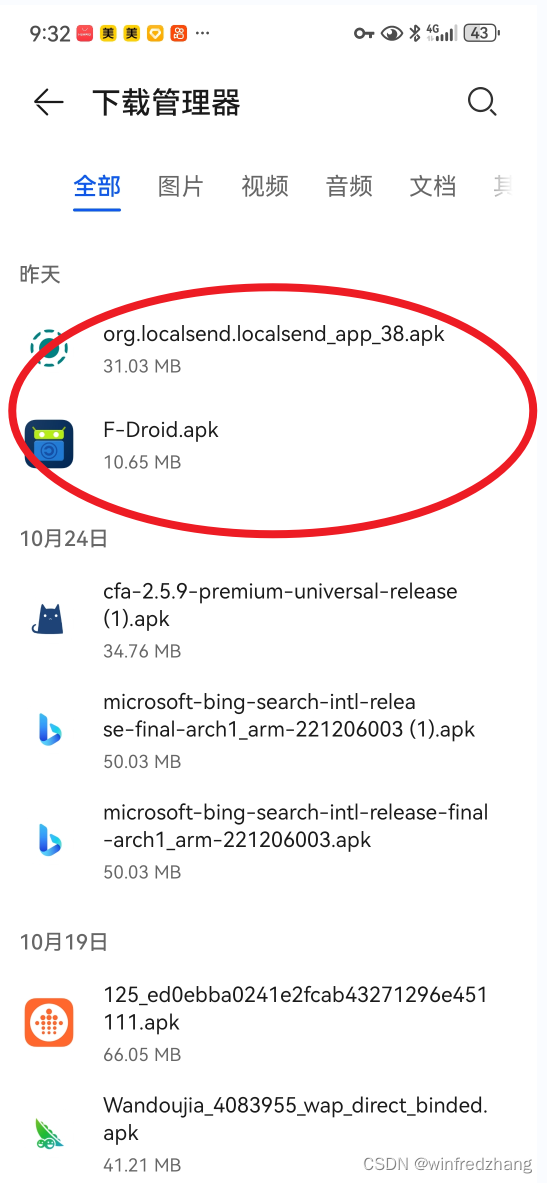
如何快速找到华为手机中下载的文档
手机的目录设置比较繁杂,尤其是查找刚刚下载的文件,有时候需要捣鼓半天,如何快速找到这些文件呢?以下提供了几种方法: 方法一: 文件管理-》搜索文档 方法二: 文件管理-》最近 方法三…...
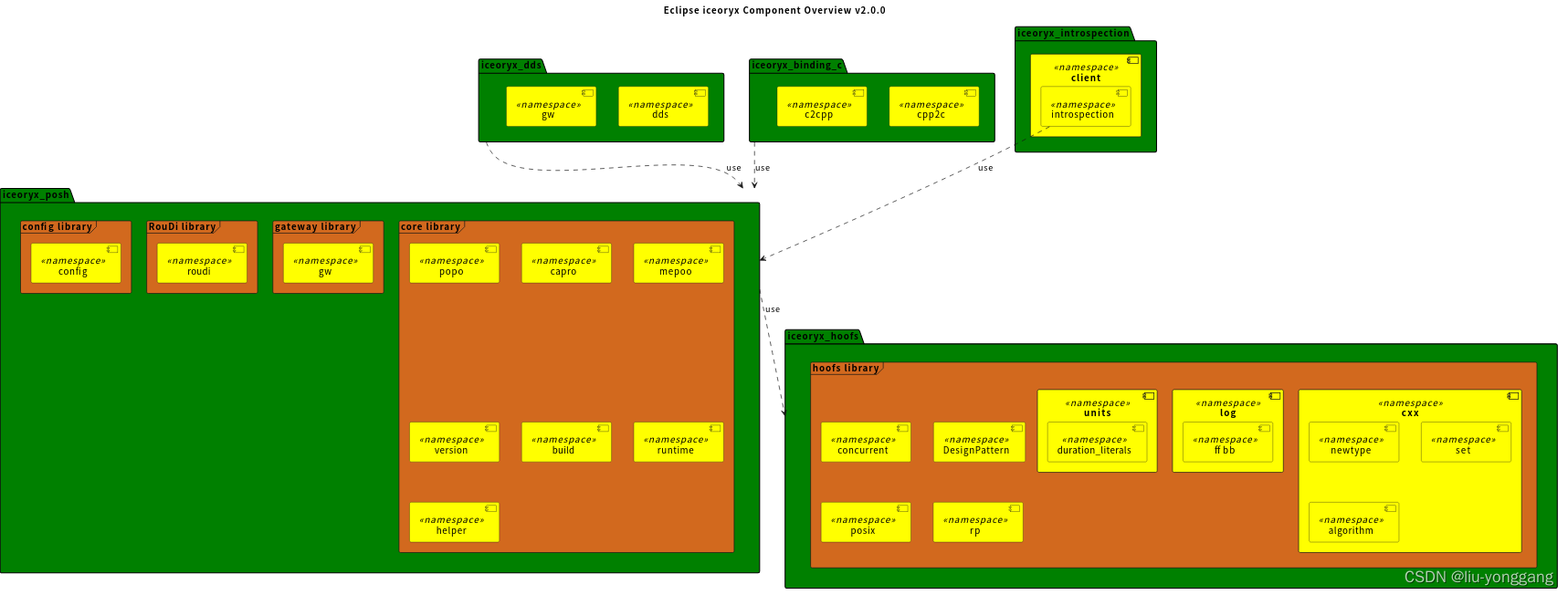
iceoryx(冰羚)-Architecture
Architecture 本文概述了Eclipseiceoryx体系结构,并解释了它的基本原理。 Software layers Eclipse iceoryx所包含的主要包如下所示。 接下来的部分将逐一简要介绍组件及其库。 Components and libraries 下面描述了不同的库及其名称空间。 ### iceoryx hoofs …...
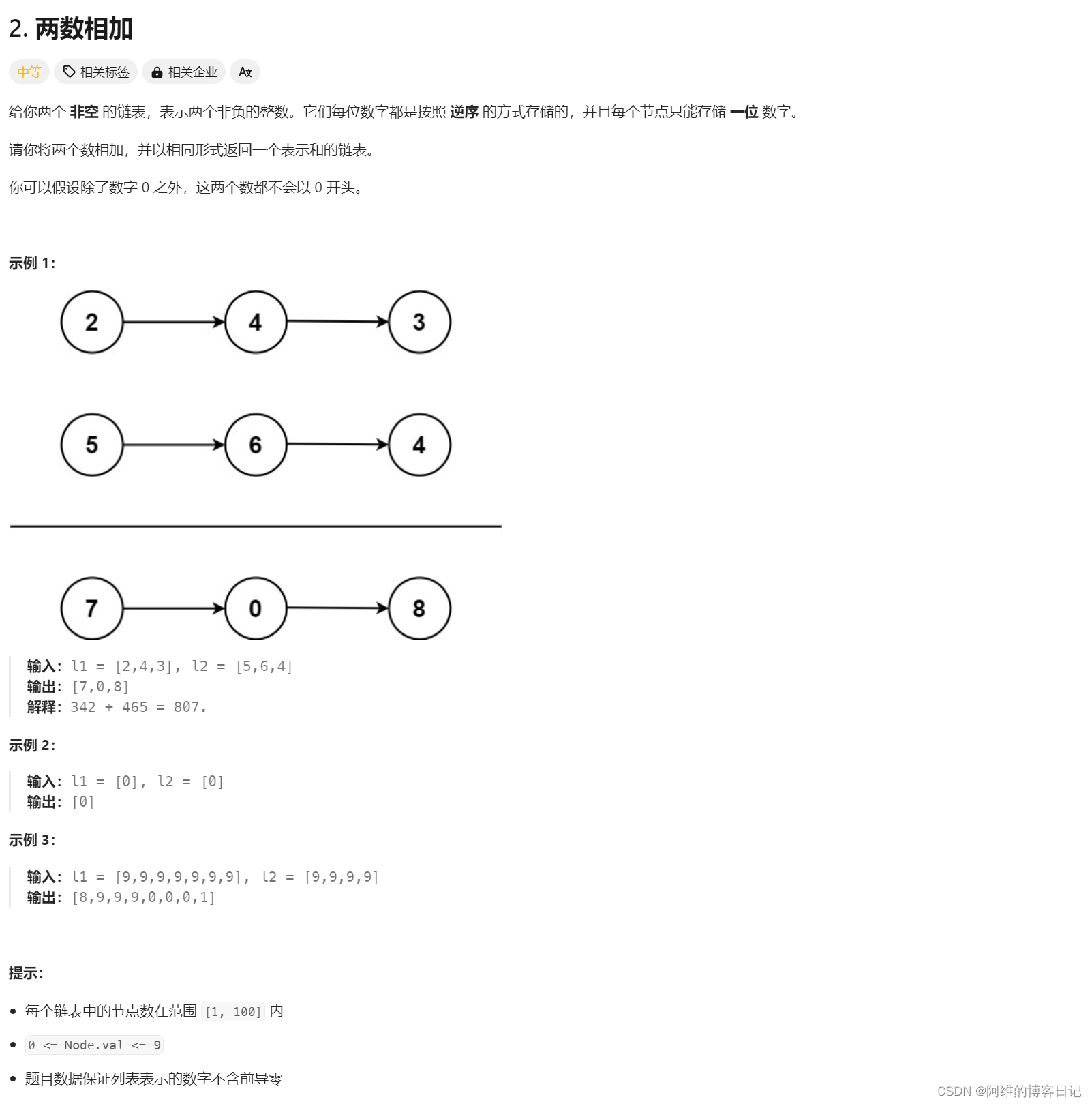
LeetCode2-两数相加
大佬解法 /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) { val x; }* }*/ class Solution {public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode pre new ListNode(0);ListNo…...

css 灰质彩色的边框
border: 4px solid transparent; background-color:#fff; background-clip: padding-box,border-box; background-origin:padding-box, border-box; background-image: linear-gradient(90deg,#F5F6FA,#F5F6FA 42%,#F5F6FA),linear-gradient(151deg,#33e9bf,#c7e58a,#b1e8cc);...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
