第一讲之递归与递推下篇
第一讲之递归与递推下篇
- 带分数
- 费解的开关
- 飞行员兄弟
- 翻硬币
带分数

用暴力将所有全排列的情况都算出来
> 有三个数,a,b,c
每种排列情况,可以用两层for循环,暴力分为三个部分,每个部分一个数
当然注意这里,第一层for循环,小于7.因为一共9个数,要保证剩下2个数不为0,要留2个位置
第二层循环,小于8,要保证剩下一个数不为0了,要留一个位置
如果边界值都写小于9的话,那么就会出现a,b,c三个数出现0的情况,这个时候,我们就要特殊的判断下
#include <iostream>using namespace std;const int N = 10;int target; // 题目给出的目标数
int num[N]; // 保存全排列的结果
bool used[N]; // 生成全排列过程中标记是否使用过
int cnt; // 计数,最后输出的结果// 计算num数组中一段的数是多少
int calc(int l, int r) {int res = 0;for (int i = l; i <= r; i++) {res = res * 10 + num[i];}return res;
}// 生成全排列
// 当全排列生成后进行分段
void dfs(int u) {// 用两层循环分成三段if (u == 9) {for (int i = 0; i < 7; i++) {for (int j = i + 1; j < 8; j++) {int a = calc(0, i);int b = calc(i + 1, j);int c = calc(j + 1, 8);// 注意判断条件,因为C++中除法是整除,所以要转化为加减乘来计算if (a * c + b == c * target) {cnt++;}}}return;}// 搜索模板for (int i = 1; i <= 9; i++) {if (!used[i]) {used[i] = true; // 标记使用num[u] = i;dfs(u + 1);used[i] = false; // 还原现场}}
}int main() {scanf("%d", &target);dfs(0);printf("%d\n", cnt);return 0;
}C++STL函数中也有现成的全排列函数(next_permutation等),可以不用自己手写
#include <bits/stdc++.h>using namespace std;const int N = 10;int target;
int num[N];int calc(int l, int r) {int res = 0;for (int i = l; i <= r; i++) {res = res * 10 + num[i];}return res;
}int main() {cin >> target;for (int i = 0; i < 9; i++) {num[i] = i + 1;}int res = 0;do {for (int i = 0; i < 9; i++) {for (int j = i + 1; j < 9; j++) {int a = calc(0, i);int b = calc(i + 1, j);int c = calc(j + 1, 8);if (a == 0 || b == 0 || c == 0) {continue;}if (a * c + b == c * target) {++res;}}}// 调用函数生成全排列} while (next_permutation(num, num + 9));cout << res << '\n';return 0;
}这主要用两层dfs嵌套来做
先dfs算出a,每个dfs算出的a中,在dfs c,b的话可以根据a与c的值来算
#include<iostream>
#include<cstdio>
#include<cstring>using namespace std;const int N = 10;int n; //目标数
bool used[N], backup[N]; //全排列的状态数组
int num[N]; //存储全排列的数据
int ans;bool check(int a, int c)
{long long b = n * (long long)c - a * c;if(!a || !b || !c) {return false;}memcpy(backup, used, sizeof used);//b是算出来的,所以b的数字是没用用到过的//因为这里要改变used[]数组,递归也在调用used数组那些//所以我们要重新创个数组while(b) {int x = b %10; //取出个位数b /= 10;if(! x|| backup[x]){return false;}backup[x] = true; //将b中用的数变为真}for(int i = 1; i <= 9; i++){if(!backup[i]){return false;}}return true;}void dfs_c(int u, int a, int c)
{if(u > 9) {return;}if(check(a, c)){ans++;}for(int i = 1;i <= 9; i++){if(!used[i]){used[i] = true;dfs_c(u + 1, a, c * 10 + i);used[i] = false; }}
} void dfs_a(int u, int a)
{if(a >= n) {return;}if(a) {dfs_c(u, a, 0);}for(int i = 1; i <= 9; i++){if(!used[i]){used[i] = true;num[u] = i;dfs_a(u + 1, a * 10 + i );used[i] = false;}}
}int main()
{scanf("%d", &n);dfs_a(0, 0);cout << ans << endl;return 0;}费解的开关
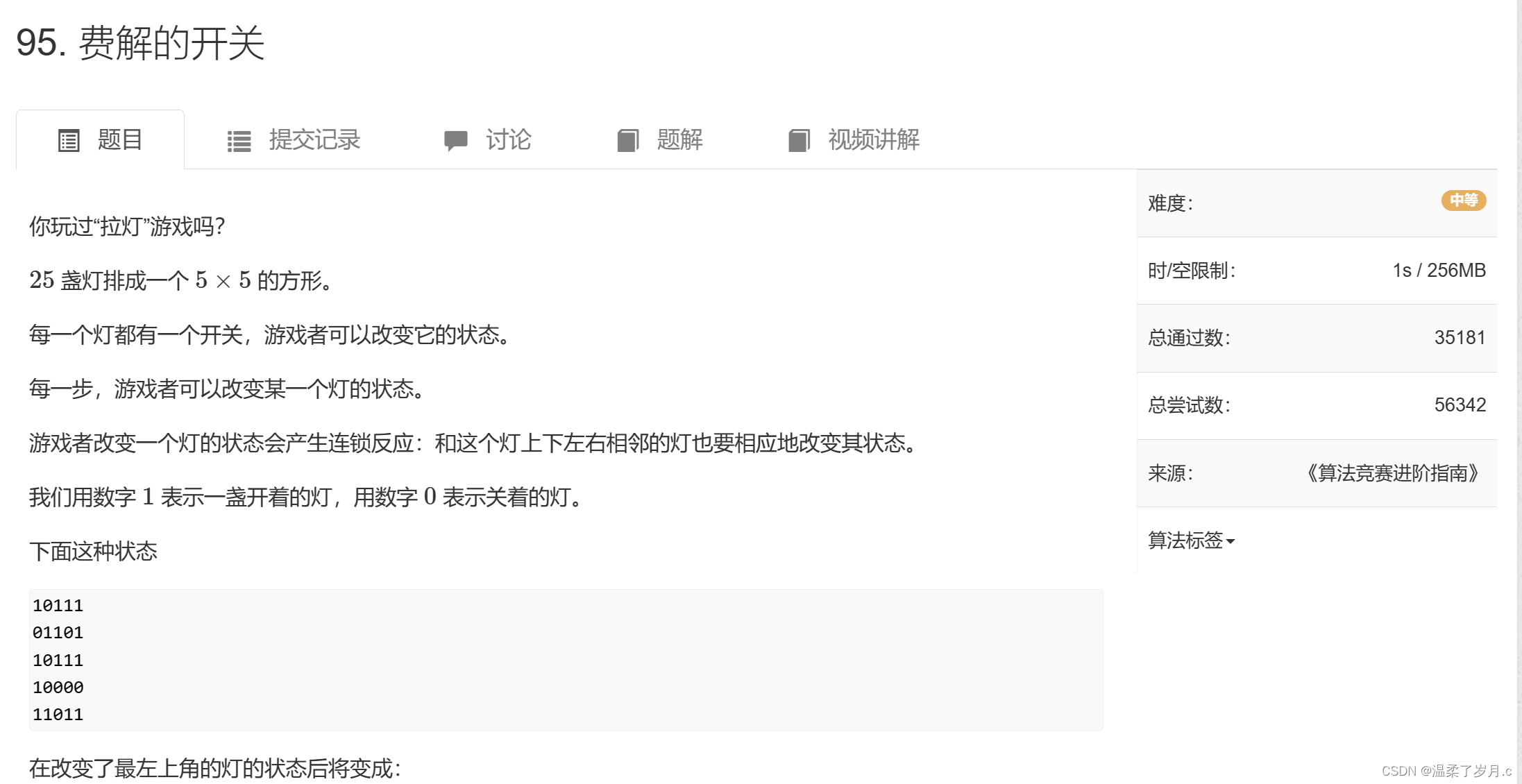
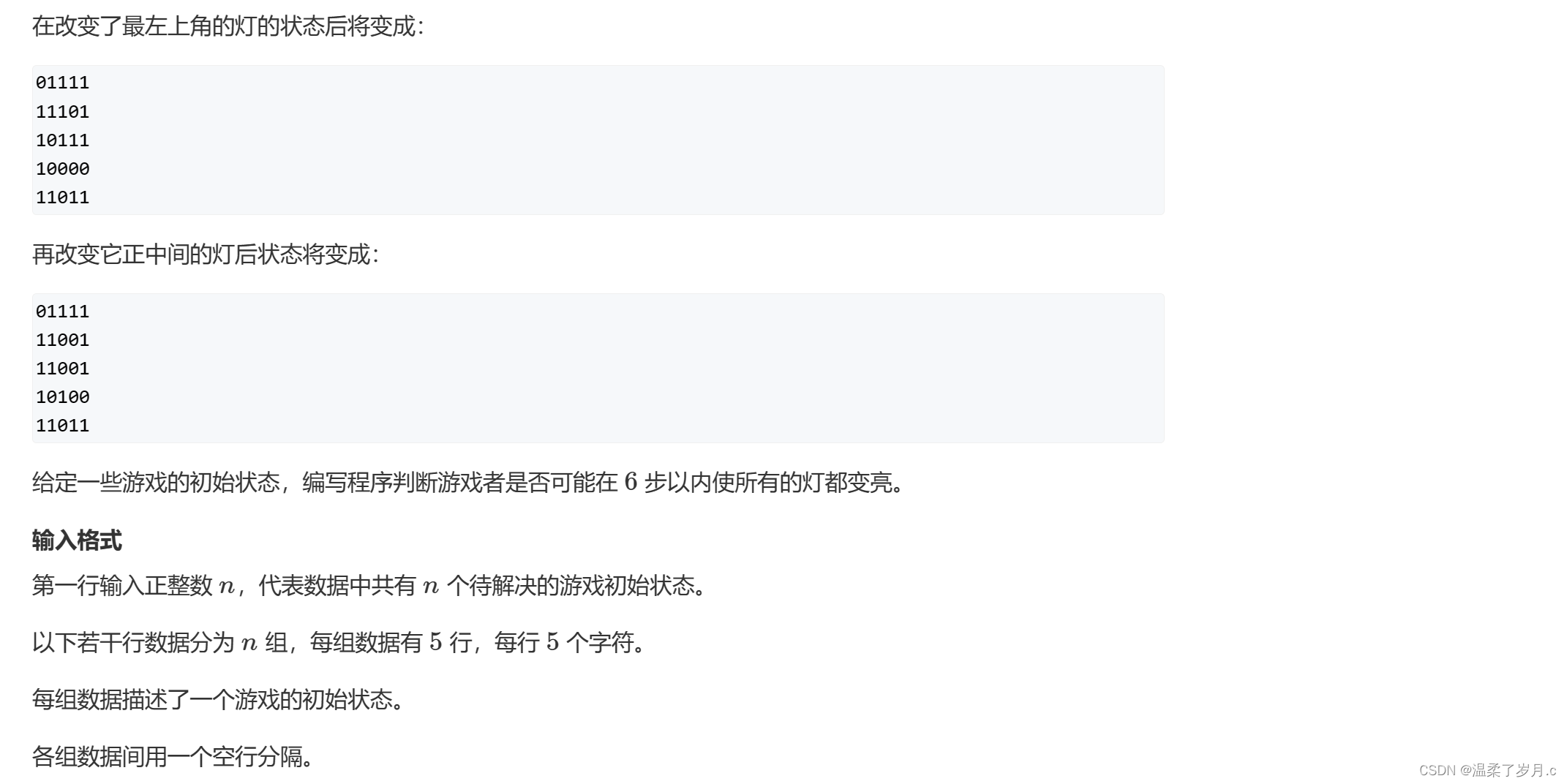
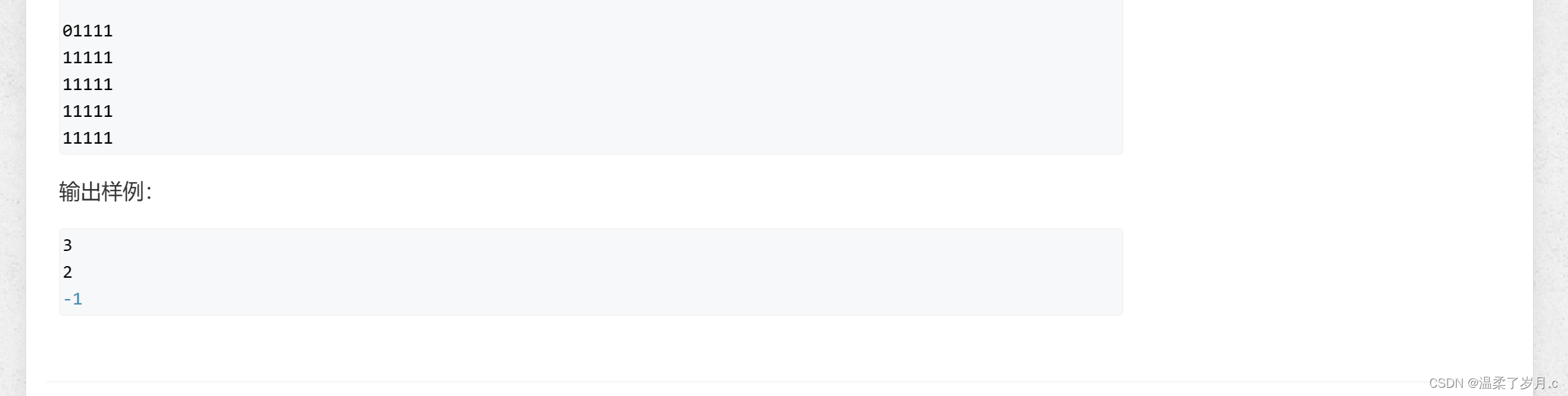
费解的开关,这道题的话,采用暴力的方法。一个开关2种状态:(选与不选)
,因为要求最优的,一个灯改变,它的上下左右相邻的回改变
解题思路:
所以我们先枚举第一行所有的情况 2^32 = 32,然后选择最优的情况
第一行枚举之后,后面依次枚举(利用下一行选开关,来改变上一行开关的状态),
但是要留下最后一行(因为最后一行,就没有下一行来改变这一行的状态了),然后检查这一行的状态
如果全是开的,说明这一行都打开了,说明这种枚举方式成功,记录下步数(与之前的比较,选择最优的)
如果不是全部开的,那么就说明枚举失败,进行下一次循环
代码部分细节讲解:
- i >> j & 1
这里其实用的是二进制的形式表示开关,对开关进行的一种优化
注意:结果的1与0,不表示开关的状态, 结果如果是1表示开关要按,为0表示开关不按
例如: 如果i为 00001, j为0, 右移0位表示00001,然后和1进行&运算,结果为1,表示开关(00001,从右往左看),第一个位置要按,j = 1, j = 2…,都表示不按,所以在开关00001这种枚举情况中,按第一个开关就行,其余开关不用按
2.这里开关状态的变化,采用的枚举的方式
3.注意每种枚举情况,都得把数据拷贝下,然后还原初始状态
#include<iostream>
#include<cstdio>
#include<cstring>using namespace std;const int N = 6;char g[N][N], backup[N][N]; //题目要求一组5个字符, 所以是char类型int dx[5] = {0,-1 , 1, 0, 0}, dy[5] = {0, 0, 0, -1, 1};void turn(int x, int y)
{for(int i = 0; i < 5; i++){//四周的开关状态改变int a = x + dx[i];int b = y + dy[i];if(a >= 0 && a < 5 && b >=0 && b < 5){g[a][b] ^= 1; //用异或来进行状态的改变}}
}int main()
{int T;cin >> T;while(T--){for(int i = 0; i < 5; i++){cin >> g[i];}int res = 10; // 题目要求步数小于6,这里用来存每种枚举情况更新的步数//枚举第一行32种情况for(int i = 0; i < 1 << 5 ; i++){int step = 0;memcpy(backup, g, sizeof g);for(int j = 0; j < 5; j++) {if(i >> j & 1){step++;turn(0, j); }}//剩下几行(除了最后一行)for(int i = 0; i < 4; i++){for(int j = 0; j < 5; j++){if(g[i][j] == '0'){step++;turn(i + 1, j); // 让上一行的打开 }}}//检查最后一行是否全部都开了bool dark = false; //判断是否关了for(int i = 0; i < 5; i++){if(g[4][i] == '0' ){dark = true;break;}}if(!dark) //最后一行全开了,比较那个步骤少 ,res更新结果{//printf("res = %d , step = %d\n", res, step);res = min(res, step); }memcpy(g, backup,sizeof backup);}if(res > 6) {cout << -1 << endl;}else{cout << res << endl;}}return 0;
}飞行员兄弟


这题的思路,跟上题费解的开关,思路差不多,不同的是上题是枚举第一行数据找最优
因为这个开关变化之后,这个开关对应的这一行,这一列都会变化,因为数据不多,
所以可以全部开关都进行暴力枚举
也是采用二进制数进行优化
枚举之后,在判断是否符合条件,当然这里需要我们输出每次改变开关的位置
我这里用vector存储的,pair类型<int, int>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>#define x first
#define y secondusing namespace std;const int N = 5;
char g[N][N], backup[N][N];//返回位置
int get(int x, int y)
{return x * 4 + y;
}void turn_one(int x, int y)
{if(g[x][y] == '+'){g[x][y] = '-';}else{g[x][y] = '+';}
}void turn_all(int x, int y)
{for(int j = 0; j < 4; j++){turn_one(x, j);turn_one(j, y);}//本身翻了2次,相当于没翻,所以还得翻一次turn_one(x, y);
}int main()
{for(int i = 0; i < 4; i++){for(int j = 0; j < 4; j++){cin >> g[i][j];}}vector<pair<int, int>> result;//枚举出所有的情况for(int pos = 0 ; pos < 1 << 16; pos++){vector<pair<int, int>> temp;memcpy(backup, g, sizeof g); for(int i = 0; i < 4; i++){for(int j = 0; j < 4; j++){if(pos >> get(i, j) & 1) //二进制的形式,为1表示需要按, 注意:这里的get(i, j) 要求得具体翻那几个位置{temp.push_back({i, j});turn_all(i, j); }}}bool has_closed = false;//看是否所有的灯都开了for(int i = 0; i < 4; i++){for(int j = 0; j < 4; j++){if(g[i][j] == '+'){has_closed = true;break;}}}if(!has_closed){if(result.empty() || result.size() > temp.size()){result = temp;}}memcpy(g, backup, sizeof backup);}cout << result.size() << endl;for(auto v : result){cout << v.first + 1 << " " << v.second + 1 << endl;}return 0;
}翻硬币
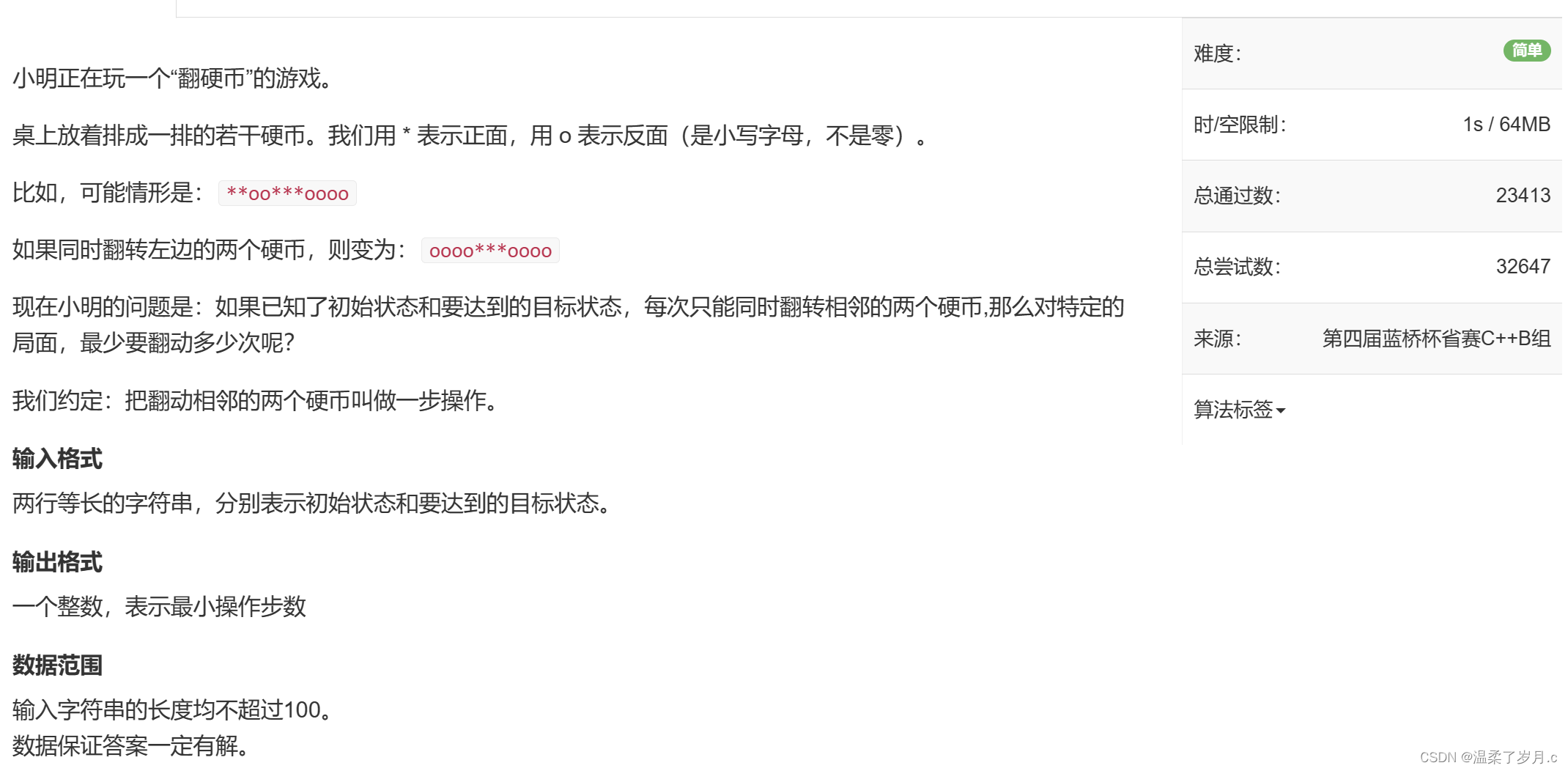
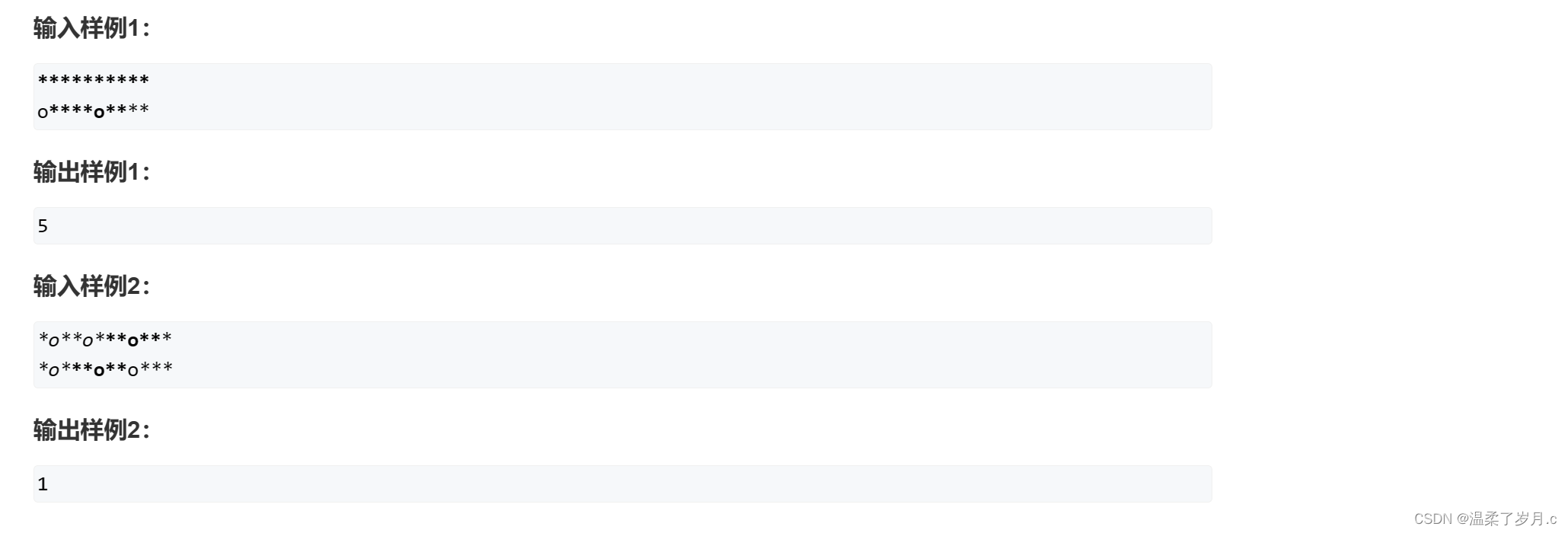
这题的话,虽然看着代码简单,但是也还是需要我们自己模拟下情况,才做的出来
判断开关的状态的话,前n- 1个就行,第n个肯定一样,因为题干说肯定有解
#include<iostream>
#include<cstdio>
#include<string>using namespace std;string a, b;void turn(int x)
{if(a[x] == 'o'){a[x] = '*';}else{a[x] = 'o';}}int main()
{cin >> a >> b;int count = 0;//前n- 1个就行,第n个肯定一样,因为题干说肯定有解for(int i = 0; i < a.size() - 1; i++){if(a[i] != b[i]){count++;turn(i);turn(i + 1);}}cout << count << endl;return 0;
}相关文章:

第一讲之递归与递推下篇
第一讲之递归与递推下篇 带分数费解的开关飞行员兄弟翻硬币 带分数 用暴力将所有全排列的情况都算出来 > 有三个数,a,b,c 每种排列情况,可以用两层for循环,暴力分为三个部分,每个部分一个数 当然注意这里,第一层fo…...

第十六篇-Awesome ChatGPT Prompts-备份
Awesome ChatGPT Prompts——一个致力于提供挖掘ChatGPT能力的Prompt收集网站 https://prompts.chat/ 2023-11-16内容如下 ✂️Act as a Linux Terminal Contributed by: f Reference: https://www.engraved.blog/building-a-virtual-machine-inside/ I want you to act as a…...

Python Web框架Django
Python Web框架Django Django简介第一个Django应用Django核心概念Django django-adminDjango项目结构Django配置文件settingsDjango创建和配置应用Django数据库配置Django后台管理Django模型Django模型字段Django模型关联关系Django模型Meta 选项Django模型属性ManagerDjango模…...

1.Spring的简单使用
简介 本文是介绍spring源码的开始,先了解最基础的使用,最深入源码。 spring源码下载地址 https://github.com/spring-projects/spring-framework.git 依赖 依赖 spring-context dependencies {implementation(project(":spring-context")…...
02.智慧商城——vant组件库使用和vw适配
01. vant组件库及Vue周边的其他组件库 组件库:第三方封装好了很多很多的组件,整合到一起就是一个组件库。 https://vant-contrib.gitee.io/vant/v2/#/zh-CN/ 比如日历组件、键盘组件、打分组件、下拉筛选组件等 组件库并不是唯一的,常用的组…...

Android笔记(十三):结合JetPack Compose和CameraX实现视频的录制和存储
在“Android笔记(八):基于CameraX库结合Compose和传统视图组件PreviewView实现照相机画面预览和照相功能”,文中介绍了拍照功能的实现,在本文中将介绍结合JetPack Compose和CameraX实现视频的录制。 新建一个项目 在项…...

【开题报告】基于SpringBoot的音乐鉴赏平台的设计与实现
1.研究背景与意义 音乐是人类文化的重要组成部分,具有广泛的影响力和吸引力。然而,随着数字化时代的到来,传统的音乐鉴赏方式面临一些挑战。因此,设计和开发一个基于Spring Boot的音乐鉴赏平台,能够满足用户对音乐欣赏…...
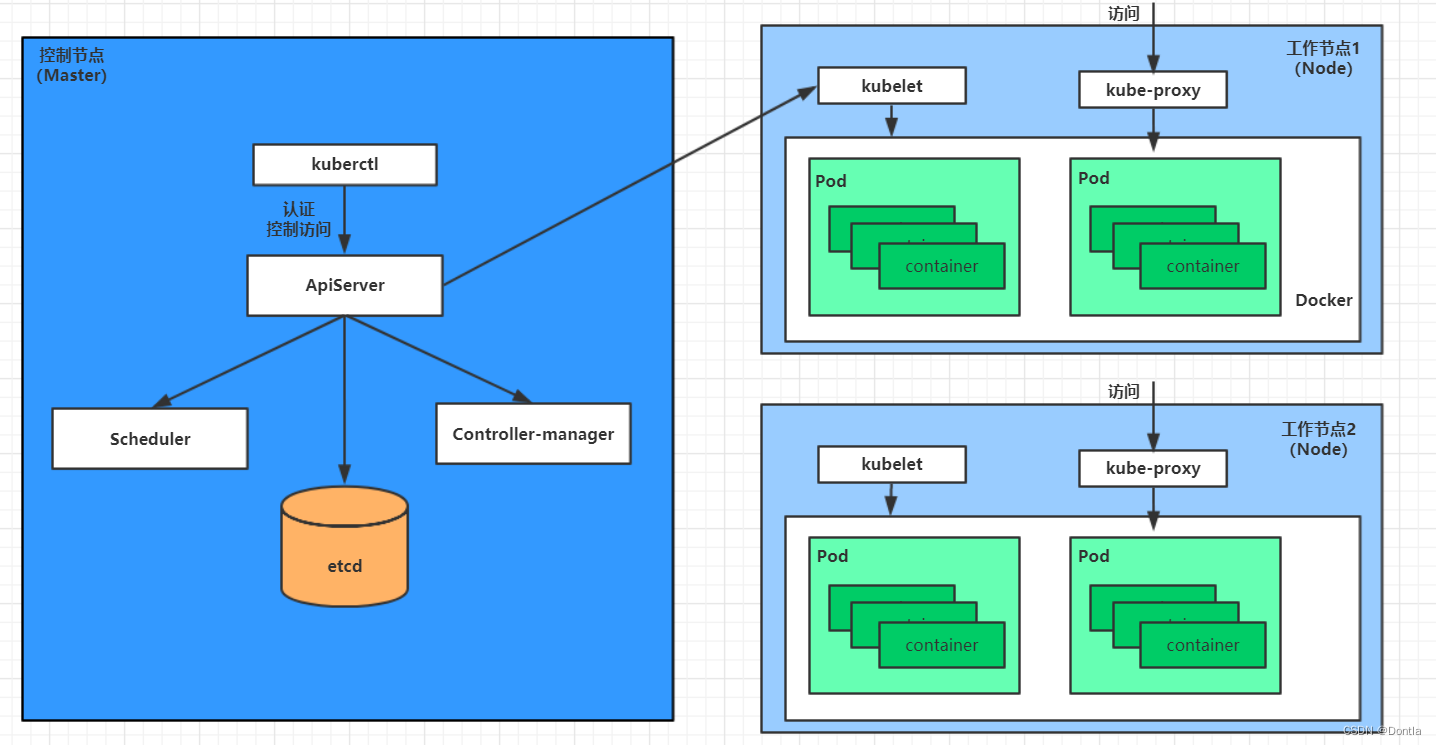
云原生 黑马Kubernetes教程(K8S教程)笔记——第一章 kubernetes介绍——Master集群控制节点、Node工作负载节点、Pod控制单元
参考文章:kubernetes介绍 文章目录 第一章 kubernetes介绍1.1 应用部署方式演变传统部署:互联网早期,会直接将应用程序部署在物理机上虚拟化部署:可以在一台物理机上运行多个虚拟机,每个虚拟机都是独立的一个环境&…...

ElasticSearch 安装(单机版本)
文章目录 ElasticSearch 安装(单机版本)环境配置下载安装包调整系统参数安装启动并验证 ElasticSearch 安装(单机版本) 此文档演示 ElasticSearch 的单机版本在 CentOS 7 环境下的安装方式以及相关的配置。 环境配置 Linux 主机一…...

读书笔记:《BackTrader 量化交易案例图解》
BackTrader 量化软件:https://github.com/mementum/backtrader -> bt 量化框架(前身):https://github.com/pmorissette/bt-> ffn 量化框架(前前身):https://github.com/pmorissette/ffn T…...

CentOS 7 免密密钥登陆sftp服务 —— 筑梦之路
为什么用sftp而不是ftp? sftp是使用ssh协议安全加密的文件传输协议,ftp在很多时候都是使用的明文传输,相对来说容易被抓包,存在安全隐患。 需求说明 1. 使用sftp代替ftp来做文件存储,锁定目录,不允许用户切…...

记一次 .NET 某券商论坛系统 卡死分析
一:背景 1. 讲故事 前几个月有位朋友找到我,说他们的的web程序没有响应了,而且监控发现线程数特别高,内存也特别大,让我帮忙看一下怎么回事,现在回过头来几经波折,回味价值太浓了。 二&#…...
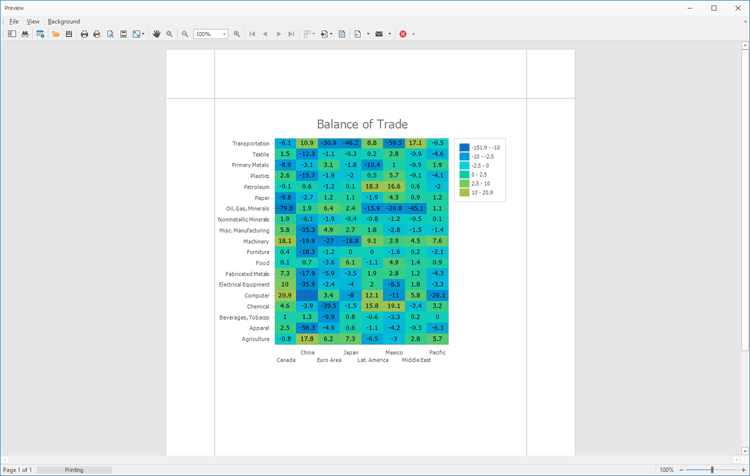
DevExpress WinForms HeatMap组件,一个高度可自定义热图控件!
通过DevExpress WinForms可以为Windows Forms桌面平台提供的高度可定制的热图UI组件,体验DevExpress的不同之处。 DevExpress WinForms有180组件和UI库,能为Windows Forms平台创建具有影响力的业务解决方案。同时能完美构建流畅、美观且易于使用的应用程…...

振弦传感器表面应变计与振弦采集仪形成岩土工程监测的解决方案
振弦传感器表面应变计与振弦采集仪形成岩土工程监测的解决方案 振弦传感器表面应变计与振弦采集仪可以结合使用,形成岩土工程监测的解决方案。具体的方案包括以下几个步骤: 1. 安装振弦传感器表面应变计:首先需要在需要监测的岩土结构表面安…...
笔记本电脑没有声音?几招恢复声音流畅!
笔记本电脑已经成为我们日常生活和工作的重要工具,而其中的声音是其功能之一。然而,有时您可能会遇到笔记本电脑没有声音的问题,这可能是由多种原因引起的。在本文中,我们将深入探讨笔记本电脑没有声音的常见原因,并提…...

JavaScript学习_01——JavaScript简介
JavaScript简介 JavaScript介绍 JavaScript是一种轻量级的脚本语言。所谓“脚本语言”,指的是它不具备开发操作系统的能力,而是只用来编写控制其他大型应用程序的“脚本”。 JavaScript 是一种嵌入式(embedded)语言。它本身提供…...
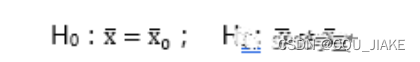
11.10~11.15置信区间,均值、方差假设检验,正态,t,卡方,F分布,第一第二类错误
置信度,置信区间 给定一个置信度,就可以算出一个置信区间。 如果给的置信度越大,那么阿尔法就越小 给的置信度越小,那么α就越大,那么 考虑精确性,希望区间长度尽可能小,所以是取正态的中间…...
)
【洛谷 P2440】木材加工 题解(二分查找+循环)
木材加工 题目背景 要保护环境 题目描述 木材厂有 n n n 根原木,现在想把这些木头切割成 k k k 段长度均为 l l l 的小段木头(木头有可能有剩余)。 当然,我们希望得到的小段木头越长越好,请求出 l l l 的最大…...

反向传播详解BP
误差反向传播(Back-propagation, BP)算法的出现是神经网络发展的重大突破,也是现在众多深度学习训练方法的基础。该方法会计算神经网络中损失函数对各参数的梯度,配合优化方法更新参数,降低损失函数。 BP本来只指损失…...
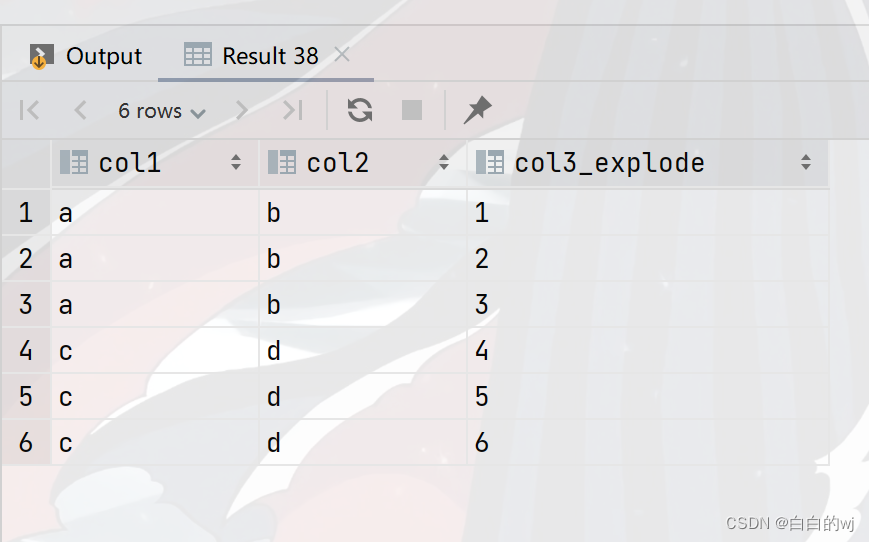
2023.11.16-hive sql高阶函数lateral view,与行转列,列转行
目录 0.lateral view简介 1.行转列 需求1: 需求2: 2.列转行 解题思路: 0.lateral view简介 hive函数 lateral view 主要功能是将原本汇总在一条(行)的数据拆分成多条(行)成虚拟表,再与原表进行笛卡尔积,…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

