《视觉SLAM十四讲》-- 后端 1(下)
8.2 BA 与图优化
Bundle Adjustment 是指从视觉图像中提炼出最优的 3D 模型和相机参数(内参和外参)。
8.2.1 相机模型和 BA 代价函数
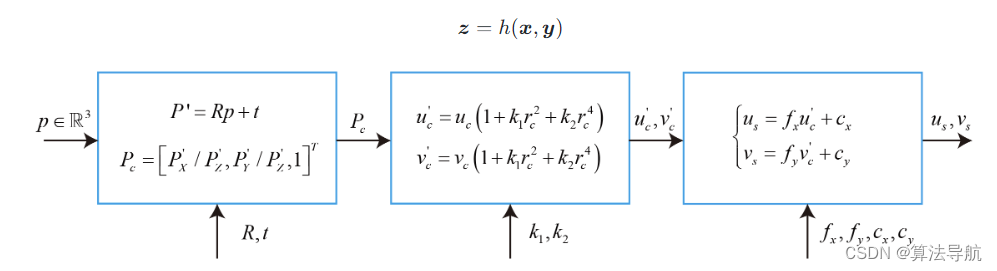
我们从一个世界坐标系中的点 p \boldsymbol{p} p 出发,把相机的内外参数和畸变都考虑进来,最后投影成像素坐标,步骤如下:
(1)世界坐标系转换到相机坐标系
P ′ = R p + t = [ X ′ , Y ′ , Z ′ ] T (8-30) \boldsymbol{P'}=\boldsymbol{Rp}+\boldsymbol{t}=[X',Y',Z']^\mathrm{T} \tag{8-30} P′=Rp+t=[X′,Y′,Z′]T(8-30)
(2)将 P ′ \boldsymbol{P'} P′ 投影至归一化平面,得到归一化坐标
P c = [ u c , v c , 1 ] T = [ X ′ / Z ′ , Y ′ / Z ′ , 1 ] T (8-31) \boldsymbol{P}_c=[u_c, v_c, 1]^{\mathrm{T}}=[X'/Z',Y'/Z', 1]^\mathrm{T} \tag{8-31} Pc=[uc,vc,1]T=[X′/Z′,Y′/Z′,1]T(8-31)
(3)去畸变(这里仅考虑径向畸变)
{ u c ′ = u c ( 1 + k 1 r c 2 + k 2 r c 4 ) v c ′ = v c ( 1 + k 1 r c 2 + k 2 r c 4 ) (8-32) \left\{\begin{array}{l} u_{\mathrm{c}}^{\prime}=u_{\mathrm{c}}\left(1+k_{1} r_{\mathrm{c}}^{2}+k_{2} r_{\mathrm{c}}^{4}\right) \\ v_{\mathrm{c}}^{\prime}=v_{\mathrm{c}}\left(1+k_{1} r_{\mathrm{c}}^{2}+k_{2} r_{\mathrm{c}}^{4}\right) \end{array}\right. \tag{8-32} {uc′=uc(1+k1rc2+k2rc4)vc′=vc(1+k1rc2+k2rc4)(8-32)
(4)根据内参模型,计算像素坐标
{ u s = f x u c ′ + c x v s = f y v c ′ + c y (8-33) \left\{\begin{array}{l} u_{s}=f_{x} u_{\mathrm{c}}^{\prime}+c_{x} \\ v_{s}=f_{y} v_{\mathrm{c}}^{\prime}+c_{y} \end{array}\right. \tag{8-33} {us=fxuc′+cxvs=fyvc′+cy(8-33)
上面的过程也就是 观测方程,将它抽象的记为
z = h ( x , y ) (8-34) \boldsymbol{z}=h({\boldsymbol{x},\boldsymbol{y}}) \tag{8-34} z=h(x,y)(8-34)
其中, x \boldsymbol{x} x 是指此时相机的位姿,即 R \boldsymbol{R} R、 t \boldsymbol{t} t,对应的李群为 T \boldsymbol{T} T,李代数为 ξ \boldsymbol{\xi} ξ;路标 y \boldsymbol{y} y 即三维点 p \boldsymbol{p} p;观测数据 z \boldsymbol{z} z 则是像素坐标。以最小二乘角度考虑,此次观测的误差为:
e = z − h ( T , p ) (8-35) \boldsymbol{e}=\boldsymbol{z}-h(\boldsymbol{T},\boldsymbol{p}) \tag{8-35} e=z−h(T,p)(8-35)
把其他时刻的观测都考虑进来,设 z i j \boldsymbol{z}_{ij} zij 为在位姿 T i \boldsymbol{T}_i Ti 处观察路标 p j \boldsymbol{p}_j pj 产生的数据,那么整体的代价函数为
1 2 ∑ i = 1 m ∑ j = 1 n ∥ e i j ∥ 2 = 1 2 ∑ i = 1 m ∑ j = 1 n ∥ z i j − h ( T i , p j ) ∥ 2 (8-36) \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{n}\|\boldsymbol{e}_{ij}\|^2=\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{n}\|\boldsymbol{z}_{ij}-h(\boldsymbol{T}_i,\boldsymbol{p}_j)\|^2 \tag{8-36} 21i=1∑mj=1∑n∥eij∥2=21i=1∑mj=1∑n∥zij−h(Ti,pj)∥2(8-36)
对这个最小二乘进行求解,相当于对位姿和路标同时进行优化,也就是所谓的 BA。
8.2.2 BA 的求解
容易看出 h ( T , p ) h(\boldsymbol{T},\boldsymbol{p}) h(T,p) 不是线性函数,因此我们希望采用非线性优化的方法求解最优值,所以关键在于梯度 Δ x \Delta \boldsymbol{x} Δx 的求解。
在整体 BA 目标函数上,我们把自变量定义为所有待优化的变量:
x = [ T 1 , T 2 , . . . , T m , p 1 , p 2 , . . . , p n ] T (8-37) \boldsymbol{x}=[\boldsymbol{T}_1,\boldsymbol{T}_2,...,\boldsymbol{T}_m,\boldsymbol{p}_1,\boldsymbol{p}_2,...,\boldsymbol{p}_n]^T \tag{8-37} x=[T1,T2,...,Tm,p1,p2,...,pn]T(8-37)
相应地,增量方程中的 Δ x \Delta \boldsymbol{x} Δx 是对整体自变量的增量。当我们给自变量一个增量时,目标函数变为:
1 2 ∥ f ( x + Δ x ) ∥ 2 ≈ 1 2 ∑ i = 1 m ∑ j = 1 n ∥ e i j + F i j Δ ξ i + E i j Δ ξ j ∥ 2 (8-38) \frac{1}{2}\|f(\boldsymbol{x}+\Delta \boldsymbol{ x})\|^2 \approx \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{n}\|\boldsymbol{e}_{ij}+\boldsymbol{F}_{ij} \Delta \boldsymbol{\xi}_i+\boldsymbol{E}_{ij}\Delta \boldsymbol{\xi}_j\|^2 \tag{8-38} 21∥f(x+Δx)∥2≈21i=1∑mj=1∑n∥eij+FijΔξi+EijΔξj∥2(8-38)
其中, F i j \boldsymbol{F}_{ij} Fij 表示整个代价函数在当前状态下对相机位姿 ξ \boldsymbol{\xi} ξ 的偏导数, E i j \boldsymbol{E}_{ij} Eij 表示整个代价函数在当前状态下路标位置 p \boldsymbol{p} p 的偏导数。
把相机位姿放在一起
x c = [ ξ 1 , ξ 2 , . . . , ξ m ] T ∈ R 6 m (8-39) \boldsymbol{x}_c=[ \boldsymbol{\xi}_1,\boldsymbol{\xi}_2,...,\boldsymbol{\xi}_m]^\mathrm{T} \in \mathbb{R}^{6m} \tag{8-39} xc=[ξ1,ξ2,...,ξm]T∈R6m(8-39)
把空间点的变量也放在一起:
x p = [ p 1 , p 2 , . . . , p n ] T ∈ R 3 n (8-40) \boldsymbol{x}_p=[ \boldsymbol{p}_1,\boldsymbol{p}_2,...,\boldsymbol{p}_n]^\mathrm{T} \in \mathbb{R}^{3n} \tag{8-40} xp=[p1,p2,...,pn]T∈R3n(8-40)
那么,式(8-38)可简化为
1 2 ∥ f ( x + Δ x ) ∥ 2 ≈ 1 2 ∥ e + F Δ x c + E Δ x p ∥ 2 (8-41) \frac{1}{2}\|f(\boldsymbol{x}+\Delta \boldsymbol{ x})\|^2 \approx \frac{1}{2}\|\boldsymbol{e}+\boldsymbol{F} \Delta \boldsymbol{x}_c+\boldsymbol{E}\Delta \boldsymbol{x}_p\|^2 \tag{8-41} 21∥f(x+Δx)∥2≈21∥e+FΔxc+EΔxp∥2(8-41)
上式将二次项之和写成了矩阵形式。这里的雅克比矩阵 F \boldsymbol{F} F 和 E \boldsymbol{E} E 是整体目标函数对整体变量的导数,它是一个很大的矩阵,由每个误差项的导数 F i j \boldsymbol{F}_{ij} Fij 和 E i j \boldsymbol{E}_{ij} Eij 拼凑而成。可以采用高斯牛顿法或 L-M 法,得到增量方程
H Δ x = g (8-42) \boldsymbol{H} \Delta \boldsymbol{x}=\boldsymbol{g} \tag{8-42} HΔx=g(8-42)
为便于表示,我们将变量归类为位姿和空间点两种,则雅克比矩阵分块为
J = [ F E ] (8-43) \boldsymbol{J=[F \quad E]} \tag{8-43} J=[FE](8-43)
以高斯牛顿法为例,则 H \boldsymbol{H} H 矩阵为
H = J T J = [ F T F F T E E T F E T E ] (8-44) \boldsymbol{H}=\boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}=\left[\begin{array}{ll} \boldsymbol{F}^{\mathrm{T}} \boldsymbol{F} & \boldsymbol{F}^{\mathrm{T}} \boldsymbol{E} \\ \boldsymbol{E}^{\mathrm{T}} \boldsymbol{F} & \boldsymbol{E}^{\mathrm{T}} \boldsymbol{E} \end{array}\right] \tag{8-44} H=JTJ=[FTFETFFTEETE](8-44)
但是,这个矩阵的维度非常大,而且直接对 H \boldsymbol{H} H 求逆,复杂度也很高。所以我们需要利用 H \boldsymbol{H} H 矩阵的特殊结构,加速计算过程。
8.2.3 稀疏性和边缘化
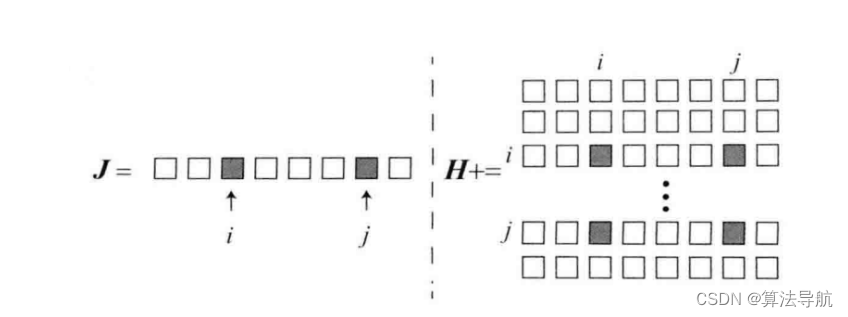
(1) H \boldsymbol{H} H 矩阵的稀疏性是由雅克比矩阵 J ( x ) \boldsymbol{J}(\boldsymbol{x}) J(x) 引起的。考虑其中一个 e i j \boldsymbol{e}_{ij} eij,它只描述了相机在 T i \boldsymbol{T}_i Ti 处看到 p j \boldsymbol{p}_j pj这件事,只与第 i i i个位姿和第 j j j 个路标有关,而与其他位姿和路标都无关,因此对其余部分的变量的导数都为零。所以误差 e i j \boldsymbol{e}_{ij} eij 对应的雅克比矩阵为
J i j ( x ) = ( 0 2 × 6 , … 0 2 × 6 , ∂ e i j ∂ T i , 0 2 × 6 , … 0 2 × 3 , … 0 2 × 3 , ∂ e i j ∂ p j , 0 2 × 3 , … 0 2 × 3 ) (8-45) \boldsymbol{J}_{i j}(\boldsymbol{x})=\left(\mathbf{0}_{2 \times 6}, \ldots \boldsymbol{0}_{2 \times 6}, \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{T}_{i}}, \mathbf{0}_{2 \times 6}, \ldots \mathbf{0}_{2 \times 3}, \ldots \mathbf{0}_{2 \times 3}, \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{p}_{j}}, \mathbf{0}_{2 \times 3}, \ldots \mathbf{0}_{2 \times 3}\right) \tag{8-45} Jij(x)=(02×6,…02×6,∂Ti∂eij,02×6,…02×3,…02×3,∂pj∂eij,02×3,…02×3)(8-45)
注意,误差对相机位姿的偏导 ∂ e i j / ∂ ξ i \partial \boldsymbol{e}_{i j} / \partial \boldsymbol{\xi}_{i} ∂eij/∂ξi 维度为 2 × 6 2\times6 2×6,对路标点的偏导 ∂ e i j / ∂ p j \partial \boldsymbol{e}_{i j} / \partial \boldsymbol{p}_{j} ∂eij/∂pj维度为 2 × 3 2\times3 2×3。
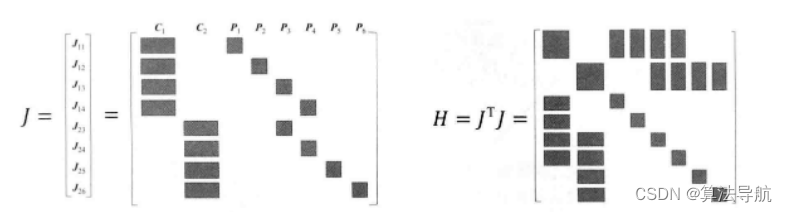
(2)以下图为例,假设 J i j \boldsymbol{J}_{ij} Jij 只在 i i i、 j j j 处有非零块,那么它对 H \boldsymbol{H} H矩阵的贡献为 J i j T J i j \boldsymbol{J}_{ij}^\mathrm{T}\boldsymbol{J}_{ij} JijTJij, J i j T J i j \boldsymbol{J}_{ij}^\mathrm{T}\boldsymbol{J}_{ij} JijTJij 矩阵有 4 个非零块,位于 ( i , i ) (i,i) (i,i)、 ( i , j ) (i,j) (i,j)、 ( j , i ) (j,i) (j,i)、 ( j , j ) (j,j) (j,j)。对整体的 H \boldsymbol{H} H,有
H = ∑ i , j J i j T J i j (8-46) \boldsymbol{H}=\sum_{i,j}\boldsymbol{J}_{ij}^\mathrm{T}\boldsymbol{J}_{ij} \tag{8-46} H=i,j∑JijTJij(8-46)
将 H \boldsymbol{H} H 矩阵分块
H = [ H 11 H 12 H 21 H 22 ] (8-47) \boldsymbol{H}=\left[\begin{array}{ll} \boldsymbol{H}_{11} & \boldsymbol{H}_{12} \\ \boldsymbol{H}_{21} & \boldsymbol{H}_{22} \end{array}\right] \tag{8-47} H=[H11H21H12H22](8-47)
结合式(8-44)可知, H 11 \boldsymbol{H}_{11} H11 只和相机位姿有关, H 22 \boldsymbol{H}_{22} H22 只和路标点有关。当遍历矩阵 H \boldsymbol{H} H时,总有:
① H 11 \boldsymbol{H}_{11} H11 是对角矩阵,且只在 H i i \boldsymbol{H}_{ii} Hii 处有非零块;
② H 22 \boldsymbol{H}_{22} H22 也是对角矩阵,且只在 H j j \boldsymbol{H}_{jj} Hjj处有非零块;
③ H 12 \boldsymbol{H}_{12} H12 和 H 21 \boldsymbol{H}_{21} H21 可能是稀疏的,也可能是稠密的,视具体观测数据而定。
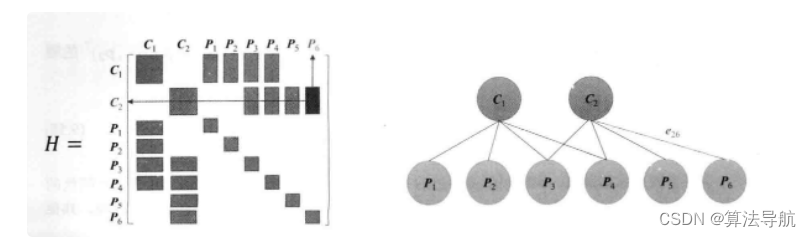
(3)以下图为例
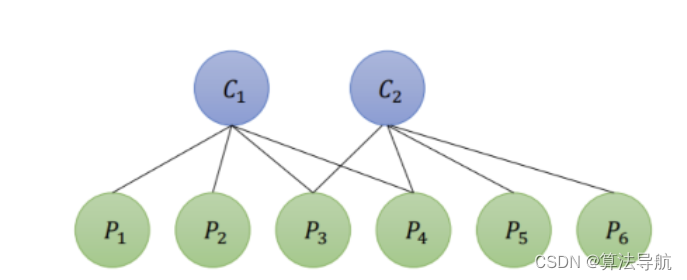
假设一个场景内,有 2 个相机位姿( C 1 \boldsymbol{C}_1 C1、 C 2 \boldsymbol{C}_2 C2)和 6 个路标点( P 1 \boldsymbol{P}_1 P1、 P 2 \boldsymbol{P}_2 P2、 P 3 \boldsymbol{P}_3 P3、 P 4 \boldsymbol{P}_4 P4、 P 5 \boldsymbol{P}_5 P5、 P 6 \boldsymbol{P}_6 P6),这些相机位姿和路标点所对应的变量为 T i , i = 1 , 2 \boldsymbol{T}_{i}, i=1,2 Ti,i=1,2 和 p j , j = 1 , 2 \boldsymbol{p}_{j}, j=1,2 pj,j=1,2。可以推出,此场景下的 BA 目标函数为:
1 2 ( ∥ e 11 ∥ 2 + ∥ e 12 ∥ 2 + ∥ e 13 ∥ 2 + ∥ e 14 ∥ 2 + ∥ e 23 ∥ 2 + ∥ e 24 ∥ 2 + ∥ e 25 ∥ 2 + ∥ e 26 ∥ 2 ) (8-48) \frac{1}{2}\left(\left\|e_{11}\right\|^{2}+\left\|e_{12}\right\|^{2}+\left\|e_{13}\right\|^{2}+\left\|e_{14}\right\|^{2}+\left\|e_{23}\right\|^{2}+\left\|e_{24}\right\|^{2}+\left\|e_{25}\right\|^{2}+\left\|e_{26}\right\|^{2}\right) \tag{8-48} 21(∥e11∥2+∥e12∥2+∥e13∥2+∥e14∥2+∥e23∥2+∥e24∥2+∥e25∥2+∥e26∥2)(8-48)
令 J 11 \boldsymbol{J}_{11} J11 为 e 11 \boldsymbol{e}_{11} e11 对应的雅克比矩阵,且 e 11 \boldsymbol{e}_{11} e11 对其他相机变量和路标点的偏导都为零。我们把所有变量以 x = ( ξ 1 , ξ 2 , p 1 , ⋯ , p 6 ) T \boldsymbol{x}=\left(\boldsymbol{\xi}_{1}, \boldsymbol{\xi}_{2}, \boldsymbol{p}_{1}, \cdots, \boldsymbol{p}_{6}\right)^{\mathrm{T}} x=(ξ1,ξ2,p1,⋯,p6)T 的顺序摆放,则有
J 11 = ∂ e 11 ∂ x = ( ∂ e 11 ∂ ξ 1 , 0 2 × 6 , ∂ e 11 ∂ p 1 , 0 2 × 3 , 0 2 × 3 , 0 2 × 3 , 0 2 × 3 , 0 2 × 3 ) (8-49) \boldsymbol{J}_{11}=\frac{\partial \boldsymbol{e}_{11}}{\partial \boldsymbol{x}}=\left(\frac{\partial \boldsymbol{e}_{11}}{\partial \boldsymbol{\xi}_{1}}, \mathbf{0}_{2 \times 6}, \frac{\partial \boldsymbol{e}_{11}}{\partial \boldsymbol{p}_{1}}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}, \mathbf{0}_{2 \times 3}\right) \tag{8-49} J11=∂x∂e11=(∂ξ1∂e11,02×6,∂p1∂e11,02×3,02×3,02×3,02×3,02×3)(8-49)
我们用下图直观地表示雅克比矩阵的稀疏性:
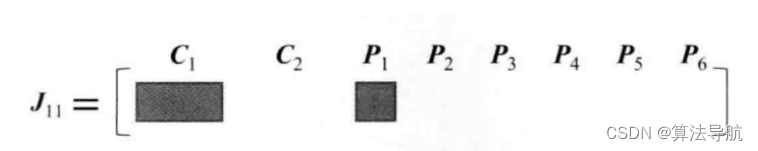
由此,可以得到整体雅克比矩阵 J \boldsymbol{J} J 和 H \boldsymbol{H} H矩阵。
H \boldsymbol{H} H 矩阵中非对角部分的非零矩阵块(长方形块)可理解为其对应的两个变量之间的关系。
更一般地,假设有 m m m 个相机位姿, n n n个路标点,且通常路标点的数量远多于相机,即 n ≫ m n \gg m n≫m。这种情况下的 H \boldsymbol{H} H 矩阵如下图所示,左上角块非常小,右下对角块很大,由于形状很像箭头,又称为箭头形矩阵。
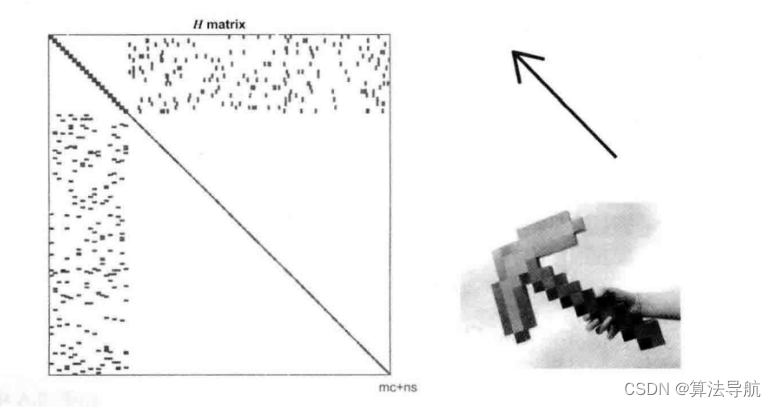
(4)将 H \boldsymbol{H} H 矩阵划分为四个区域,不难看出,左上角为对角块矩阵,且每个对角块元素的维度与相机位姿维度相同,同样的,右下角也是对角块矩阵,且每个对角块元素的维度与路标点维度相同。而且这四个区域和式(8-44)中的矩阵块是对应的。

那么,增量方程 H Δ x = g \boldsymbol{H} \Delta\boldsymbol{x}=\boldsymbol{g} HΔx=g 可写为以下形式
[ B E E T C ] [ Δ x c Δ x p ] = [ v w ] (8-50) \left[\begin{array}{cc} \boldsymbol{B} & \boldsymbol{E} \\ \boldsymbol{E}^{\mathrm{T}} & \boldsymbol{C} \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{x}_{\mathrm{c}} \\ \Delta \boldsymbol{x}_{p} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{v} \\ \boldsymbol{w} \end{array}\right] \tag{8-50} [BETEC][ΔxcΔxp]=[vw](8-50)
对角块矩阵求逆的难度远小于一般矩阵的求逆难度,所以只需要对对角块矩阵分别求逆即可。对线性方程组进行高斯消元,得
[ I − E C − 1 0 I ] [ B E E T C ] [ Δ x c Δ x p ] = [ I − E C − 1 0 I ] [ v w ] (8-51) \left[\begin{array}{cc} \boldsymbol{I} & -\boldsymbol{E} \boldsymbol{C}^{-1} \\ \mathbf{0} & \boldsymbol{I} \end{array}\right]\left[\begin{array}{cc} \boldsymbol{B} & \boldsymbol{E} \\ \boldsymbol{E}^{\mathrm{T}} & C \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{x}_{\mathrm{c}} \\ \Delta \boldsymbol{x}_{p} \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{I} & -\boldsymbol{E} \boldsymbol{C}^{-1} \\ 0 & \boldsymbol{I} \end{array}\right]\left[\begin{array}{l} \boldsymbol{v} \\ \boldsymbol{w} \end{array}\right] \tag{8-51} [I0−EC−1I][BETEC][ΔxcΔxp]=[I0−EC−1I][vw](8-51)
整理,得
[ B − E C − 1 E T 0 E T C ] [ Δ x c Δ x p ] = [ v − E C − 1 w w ] (8-52) \left[\begin{array}{cc} \boldsymbol{B}-\boldsymbol{E} \boldsymbol{C}^{-1}\boldsymbol{E}^{\mathrm{T}} & \boldsymbol{0} \\ \boldsymbol{E}^{\mathrm{T}} & \boldsymbol{C} \end{array}\right]\left[\begin{array}{l} \Delta \boldsymbol{x}_{\mathrm{c}} \\ \Delta \boldsymbol{x}_{p} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{v}-\boldsymbol{E} \boldsymbol{C}^{-1} \boldsymbol{w} \\ \boldsymbol{w} \end{array}\right] \tag{8-52} [B−EC−1ETET0C][ΔxcΔxp]=[v−EC−1ww](8-52)
可以看出,方程第一行只和 Δ x c \Delta \boldsymbol{x}_c Δxc 有关,我们可以先将 Δ x c \Delta \boldsymbol{x}_c Δxc 解出来:
( B − E C − 1 E T ) Δ x c = v − E C − 1 w (8-53) (\boldsymbol{B}-\boldsymbol{E} \boldsymbol{C}^{-1}\boldsymbol{E}^{\mathrm{T}})\Delta \boldsymbol{x}_c=\boldsymbol{v}-\boldsymbol{E} \boldsymbol{C}^{-1} \boldsymbol{w} \tag{8-53} (B−EC−1ET)Δxc=v−EC−1w(8-53)
Δ x c \Delta \boldsymbol{x}_c Δxc 解出来后,再将其代入第二行方程,从而将 Δ x p \Delta \boldsymbol{x}_p Δxp 求解出来。这个过程称为 Schur (舒尔)消元。相较于直接求解的方法,它的优势在于:
① 消元过程中, C \boldsymbol{C} C 为对角块,故 C − 1 \boldsymbol{C}^{-1} C−1 容易求出;
② Δ x c \Delta \boldsymbol{x}_c Δxc 解出来后,根据 Δ x p = C − 1 ( w − E T Δ x c ) \Delta \boldsymbol{x}_{p}=\boldsymbol{C}^{-1}\left(\boldsymbol{w}-\boldsymbol{E}^{\mathrm{T}} \Delta \boldsymbol{x}_{\mathrm{c}}\right) Δxp=C−1(w−ETΔxc) 解出路标的增量方程。
(5)从概率角度来看,我们称这一步为 边缘化。我们将求解 ( Δ x c , Δ x p ) (\Delta \boldsymbol{x}_c,\Delta \boldsymbol{x}_p) (Δxc,Δxp) 的问题,转化成了先固定 Δ x p \Delta \boldsymbol{x}_p Δxp,求出 Δ x c \Delta \boldsymbol{x}_c Δxc,再求 Δ x p \Delta \boldsymbol{x}_p Δxp 的过程。这相当于做了条件概率展开:
P ( x c , x p ) = P ( x c ∣ x p ) P ( x p ) (8-54) P(\boldsymbol{x}_c,\boldsymbol{x}_p)=P( \boldsymbol{x}_c | \boldsymbol{x}_p)P(\boldsymbol{x}_p) \tag{8-54} P(xc,xp)=P(xc∣xp)P(xp)(8-54)
8.2.4 鲁棒核函数
在前面的 BA 问题中,我们将最小化误差项的二范数平方和作为目标函数,这样虽然直观,但是如果出现误匹配,该误差项会很大,从而将对整体函数产生较大影响,进而影响最终优化结果。
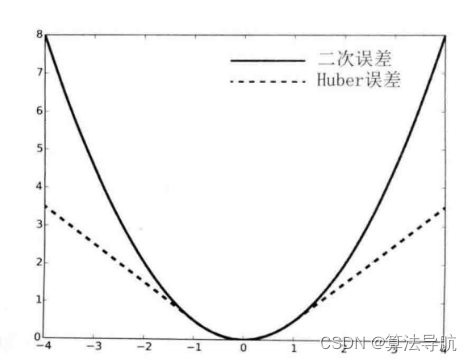
对此,我们将原先误差的二范数度量替换成一个增长没那么快的函数,同时保证光滑性质,使得优化结果更加稳健(减小误匹配项的影响),这样的函数称为 鲁棒核函数。鲁棒核函数有很多种,如 Huber 核:
H ( e ) = { 1 2 e 2 当 ∣ e ∣ ⩽ δ , δ ( ∣ e ∣ − 1 2 δ ) 其他 (8-55) H(e)= \begin{cases}\frac{1}{2} e^{2} & \text { 当 }|e| \leqslant \delta, \\ \delta\left(|e|-\frac{1}{2} \delta\right) & \text { 其他 }\end{cases} \tag{8-55} H(e)={21e2δ(∣e∣−21δ) 当 ∣e∣⩽δ, 其他 (8-55)
当误差 e e e 大于阈值 δ \delta δ 时,函数增长由二次形式转为一次形式,相当于限制了梯度的最大值。同时 Huber 核函数又是光滑的,可以很方便的求导。如下图,在误差较大时,Huber 核函数增长明显低于二次函数。
相关文章:

《视觉SLAM十四讲》-- 后端 1(下)
8.2 BA 与图优化 Bundle Adjustment 是指从视觉图像中提炼出最优的 3D 模型和相机参数(内参和外参)。 8.2.1 相机模型和 BA 代价函数 我们从一个世界坐标系中的点 p \boldsymbol{p} p 出发,把相机的内外参数和畸变都考虑进来,…...

io+day8
#ifndef __SEM2 #define __SEM3 4 //声明一个创>5 int init_sem(6 7 //声明一个p操8 int P(int sem9 10 //声明一个v操11 int W(int sem12 13 //声明一个删>14 int del_sem(i15 16 #endif 1 #include <myhead.h> …...

【图像处理:OpenCV-Python基础操作】
【图像处理:OpenCV-Python基础操作】 1 读取图像2 显示图像3 保存图像4 图像二值化、灰度图、彩色图,像素替换5 通道处理(通道拆分、合并)6 调整尺寸大小7 提取感兴趣区域、掩膜8 乘法、逻辑运算9 HSV色彩空间,获取特定…...

Java 简单实现一个 TCP 回显服务器
文章目录 TCP 服务端TCP 客户端实现效果TCP 服务端(实现字典功能)总结 TCP 服务端 package network;import java.io.IOException; import java.io.InputStream; import java.io.OutputStream; import java.io.PrintWriter; import java.net.ServerSocket; import java.net.Soc…...

邦芒攻略:新手求职面试需要准备的材料
新手求职面试需要准备的材料,求职材料是求职者写给用人单位的信,目的是让对方了解自己,准备好充足的资料和自信的心态会让面试通过的几率大大增强,那么应聘者需要准备的材料呢,来看看吧。 1、求职信。也是求职者…...
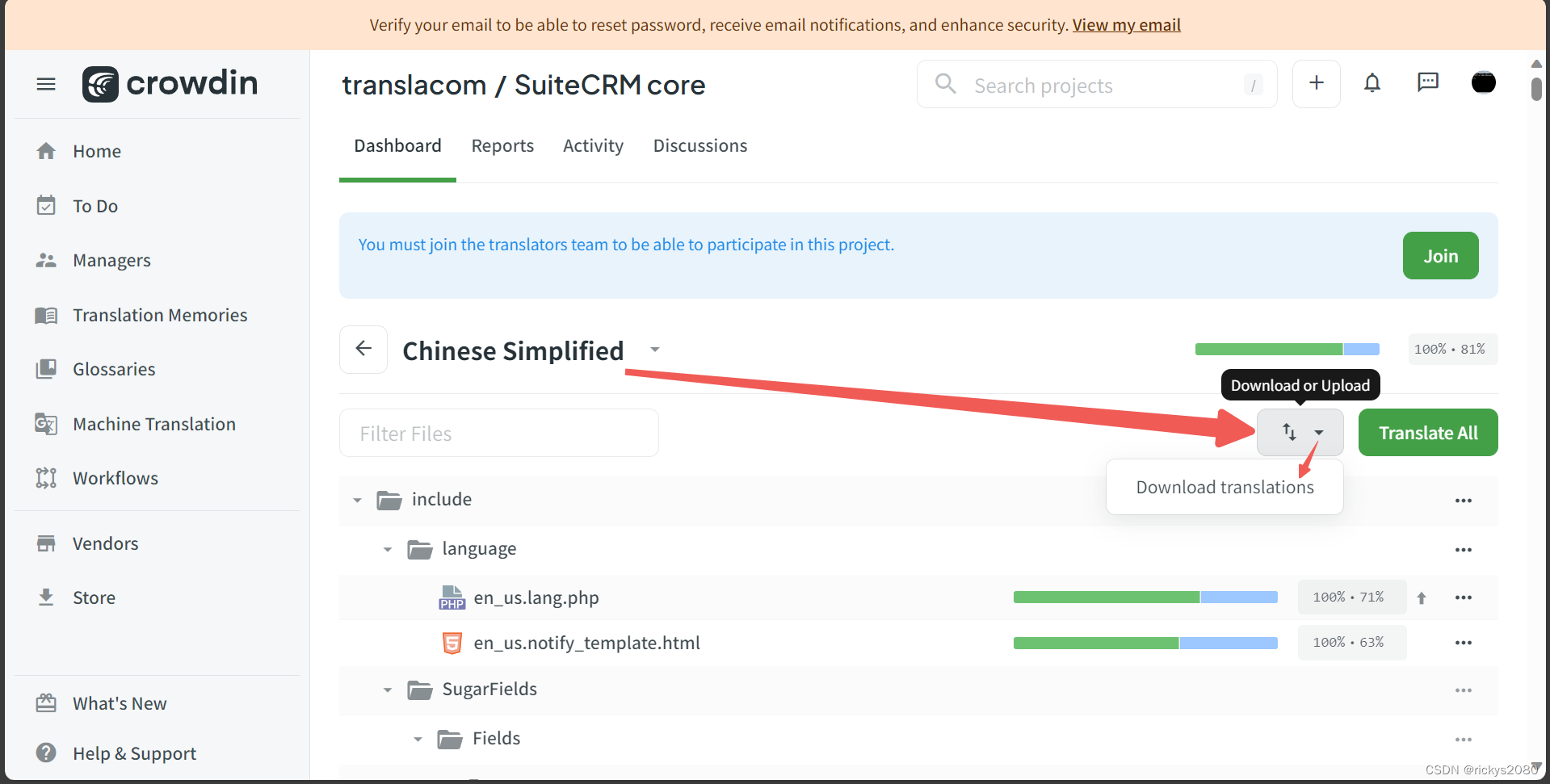
在docker下安装suiteCRM
安装方法: docker-hub来源:https://hub.docker.com/r/bitnami/suitecrm curl -sSL https://raw.githubusercontent.com/bitnami/containers/main/bitnami/suitecrm/docker-compose.yml > docker-compose.yml//然后可以在docker-compose.yml文件里修…...

【Python大数据笔记_day08_hive查询】
hive查询 语法结构: SELECT [ALL | DISTINCT] 字段名, 字段名, ... FROM 表名 [inner | left outer | right outer | full outer | left semi JOIN 表名 ON 关联条件 ] [WHERE 非聚合条件] [GROUP BY 分组字段名] [HAVING 聚合条件] [ORDER BY 排序字段名 asc | desc] [CLUSTE…...

魔众文库系统 v5.6.0 DWG文件格式支持,部分数据封面显示异常,定时调度清理临时文件
魔众文库系统基于文档系统知识,建立平台与领域,打造流量、用户、付费和变现的闭环,帮助您更好的搭建文库系统。 魔众文库系统发布v5.6.0版本,新功能和Bug修复累计17项,DWG文件格式支持,部分数据封面显示异…...

2023 PostgreSQL 数据库生态大会:解读拓数派大数据计算系统及其云存储底座
11月3日-5日,由中国开源软件推进联盟 PostgreSQL 分会主办的中国 PostgreSQL 数据库生态大会在北京中科院软件所隆重举行。大会以”极速进化融合新生”为主题,从线下会场和线上直播两种方式展开,邀请了数十位院士、教授、高管和社群专家&…...
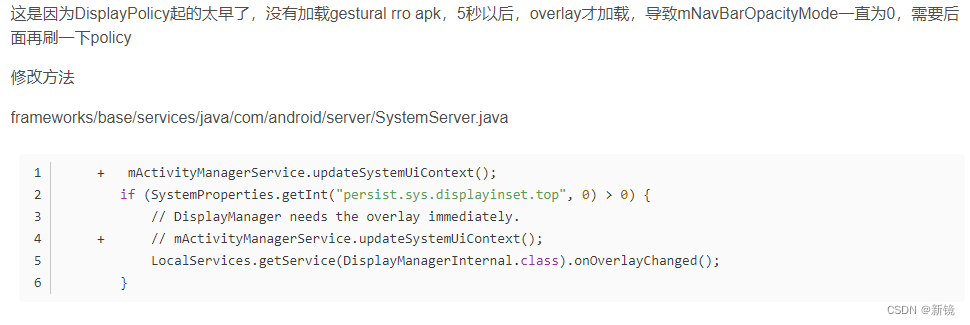
Android10 手势导航
种类 Android10 默认的系统导航有三种: 1.两个按钮的 2.三个按钮的 3.手势 它们分别对应三个包名 frameworks/base/packages/overlays/NavigationBarMode2ButtonOverlay frameworks/base/packages/overlays/NavigationBarMode3ButtonOverlay frameworks/base/packa…...

Pinia 插件 pinia-plugin-persist 添加 persist 属性时报错:没有与此调用匹配的重载
项目场景: Vue3TS 语言Pinia插件:pinia-plugin-persist 问题描述 代码如下: import { defineStore } from piniaexport const useInfoStore defineStore(info, {state: () > {return {activeIndex: 0}},actions: {updateIndex(active…...

Django知识
目录 一.request对象方法 1.request.method 2.request.POST 3.request.GET 4.request.FILES 5.request.path 二.FBV与CBV引入 1.FBV 2.CBV (1)路由 (2)视图 3.详解 (1)FBV (2)CBV (3)小结 三.CBV源码剖析 1.as_view方法 (1)路由对应函…...
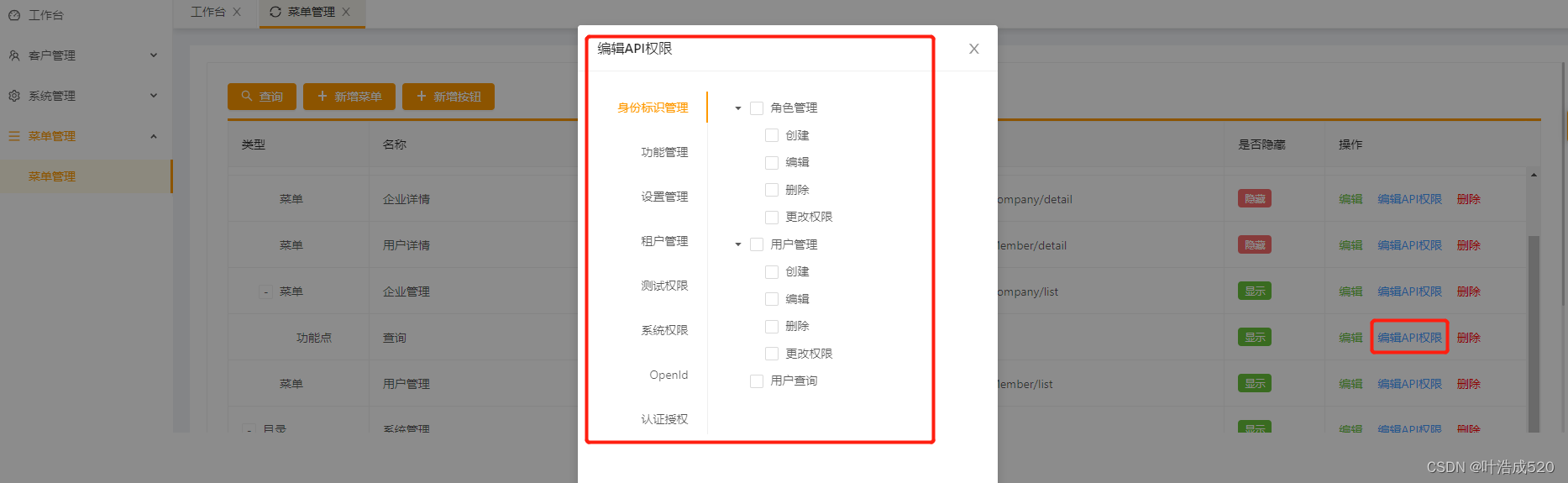
vue2+antd——实现权限管理——js数据格式处理(回显+数据结构渲染)
vue2antd——实现权限管理——js数据格式处理 效果图如下:1.需求说明2.如何展开所有子项及孙子项目——在弹窗之前就获取树形结构,然后直接将数据传到弹窗中3.template部分代码4.script的data部分5.权限tree数据处理——将row中的权限分配到具体的value参…...
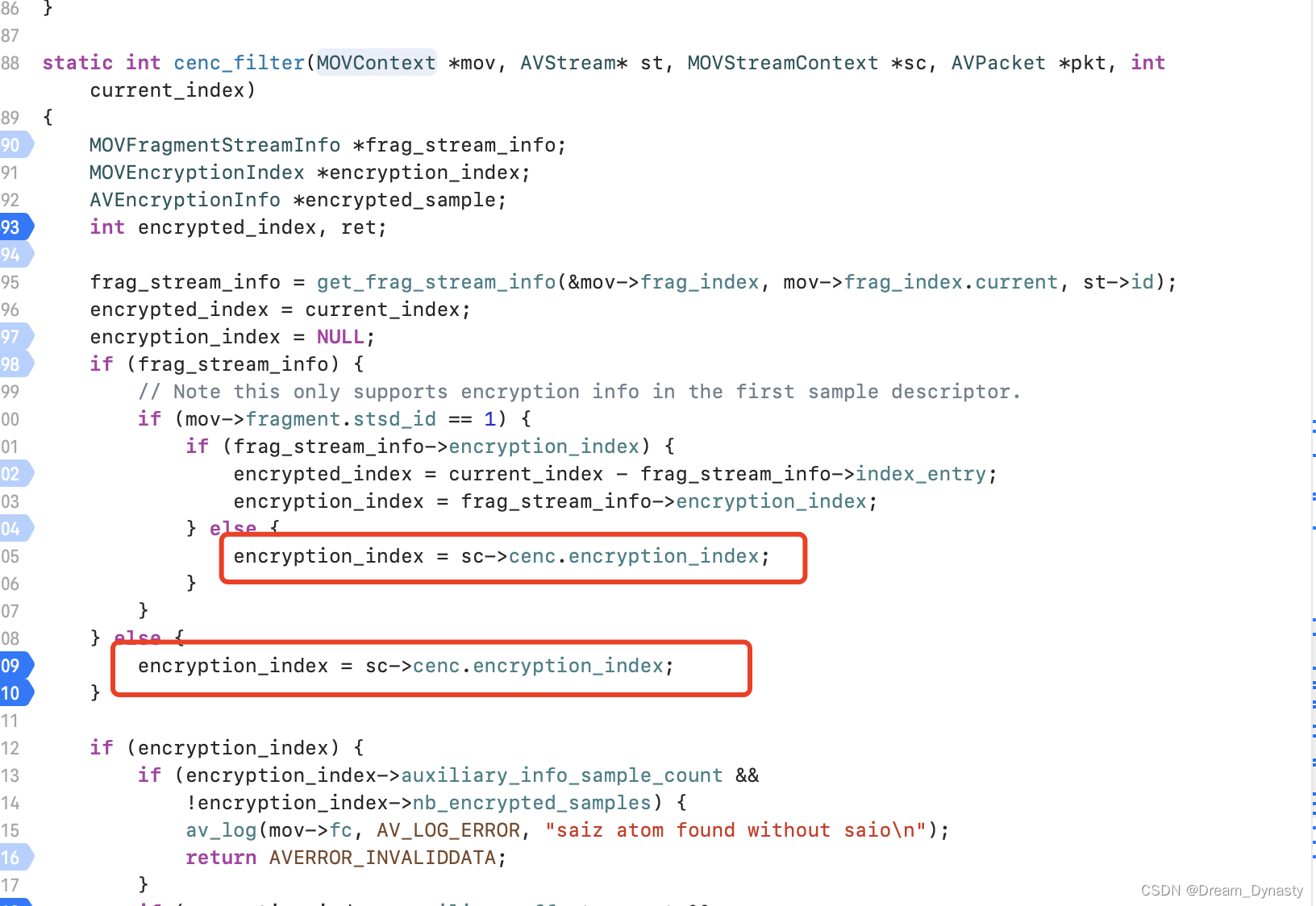
ffmpeg 4.4 cenc-aes-ctr 加解密 MP4 工程性质分析
目录 一、cenc-aes-ctr 原理介绍 二、显式 cenc-aes-ctr 和隐式 cenc-aes-ctr 三、加密工具---ffmpeg 四、播放---ffplay 五、总结 一、cenc-aes-ctr 原理介绍 加密算法:CENC-AES-CTR 使用 AES(Advanced Encryption Standard&…...
网络安全/黑客技术(0基础入门到进阶提升)
前言 前几天发布了一篇 网络安全(黑客)自学 没想到收到了许多人的私信想要学习网安黑客技术!却不知道从哪里开始学起!怎么学 今天给大家分享一下,很多人上来就说想学习黑客,但是连方向都没搞清楚就开始学习…...
栈的三道oj【C++】
栈和队列的相关oj 最小栈思路解决代码 栈的压入弹出序列思路解决代码 逆波兰表达式思路:解决代码 这里就挑了三道题用来熟悉栈 最小栈 力扣链接 咱们已经是高贵的C使用者了,不用像C语言一样从头开始造轮子了 这里我们调用了stack后,就会发…...

AI大模型低成本快速定制法宝:RAG和向量数据库
文章目录 1. 前言2. RAG和向量数据库3. 论坛日程4. 购票方式 1. 前言 当今人工智能领域,最受关注的毋庸置疑是大模型。然而,高昂的训练成本、漫长的训练时间等都成为了制约大多数企业入局大模型的关键瓶颈。 这种背景下,向量数据库凭借其独特…...

文旅媒体有哪些?如何邀请到现场报道?
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 中国文旅产业在近年来得到了持续而快速的发展。从产业端看,中国文旅产业呈现出新的发展趋势,其中“文旅”向“文旅”转变成为显著特点。通过产业升级和空间构建&a…...

搭建知识付费系统的最佳实践是什么
在数字化时代,搭建一个高效且用户友好的知识付费系统是许多创业者和内容创作者追求的目标。本文将介绍一些搭建知识付费系统的最佳实践,同时提供一些基本的技术代码示例,以帮助你快速入门。 1. 选择合适的技术栈: 搭建知识付费…...

计算机视觉:使用opencv实现车牌识别
1 引言 汽车车牌识别(License Plate Recognition)是一个日常生活中的普遍应用,特别是在智能交通系统中,汽车牌照识别发挥了巨大的作用。汽车牌照的自动识别技术是把处理图像的方法与计算机的软件技术相连接在一起,以准…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
