【LeetCode】2363. 合并相似的物品
2363. 合并相似的物品
题目描述
给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质:
- items[i] = [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,weighti 表示第 i 件物品的 重量 。
- items 中每件物品的价值都是 唯一的 。
请你返回一个二维数组 ret,其中 ret[i] = [valuei, weighti], weighti 是所有价值为 valuei 物品的 重量之和 。
注意:ret 应该按价值 升序 排序后返回。
示例 1
输入:items1 = [[1,1],[4,5],[3,8]], items2 = [[3,1],[1,5]]
输出:[[1,6],[3,9],[4,5]]
解释:
value = 1 的物品在 items1 中 weight = 1 ,在 items2 中 weight = 5 ,总重量为 1 + 5 = 6 。
value = 3 的物品再 items1 中 weight = 8 ,在 items2 中 weight = 1 ,总重量为 8 + 1 = 9 。
value = 4 的物品在 items1 中 weight = 5 ,总重量为 5 。
所以,我们返回 [[1,6],[3,9],[4,5]] 。
示例 2
输入:items1 = [[1,1],[3,2],[2,3]], items2 = [[2,1],[3,2],[1,3]]
输出:[[1,4],[2,4],[3,4]]
解释:
value = 1 的物品在 items1 中 weight = 1 ,在 items2 中 weight = 3 ,总重量为 1 + 3 = 4 。
value = 2 的物品在 items1 中 weight = 3 ,在 items2 中 weight = 1 ,总重量为 3 + 1 = 4 。
value = 3 的物品在 items1 中 weight = 2 ,在 items2 中 weight = 2 ,总重量为 2 + 2 = 4 。
所以,我们返回 [[1,4],[2,4],[3,4]] 。
示例 3
输入:items1 = [[1,3],[2,2]], items2 = [[7,1],[2,2],[1,4]]
输出:[[1,7],[2,4],[7,1]]
解释:
value = 1 的物品在 items1 中 weight = 3 ,在 items2 中 weight = 4 ,总重量为 3 + 4 = 7 。
value = 2 的物品在 items1 中 weight = 2 ,在 items2 中 weight = 2 ,总重量为 2 + 2 = 4 。
value = 7 的物品在 items2 中 weight = 1 ,总重量为 1 。
所以,我们返回 [[1,7],[2,4],[7,1]] 。
提示
- 1 <= items1.length, items2.length <= 1000
- items1[i].length == items2[i].length == 2
- 1 <= valuei, weighti <= 1000
- items1 中每个 valuei 都是 唯一的 。
- items2 中每个 valuei 都是 唯一的 。
算法一:map 和 vector 的转化
思路
- 首先将 items1 里的 value 和 weight 转换为 map 对应的 键值对,由于 map 会默认对 key 升序排序,因此此时的顺序已经满足了题目的要求。
- 接着遍历 items2 ,将 items2 中对应的物品也加入到 map 中。
- 此时 map 里存储的键值对就是答案,但是这道题要求我们返回二维 vector ,因此还需要将 map 转化为 二维 vector。
收获
- 一开始想要哈希表,但是如果用下标存储 value ,太浪费空间了;如果是使用二维数组作为哈希表,遍历 items2 的时候又难以获得 value ,最后看了提示,可以用 map 。
- map 访问对象 , key - map.first , value - map.second;
- 如何将 map 转化为 二维 vector :这个我想了很久,后来发现可以创建一维 vector,将 map.first 和 map.second 放入,再将一维数组 push_back 到二维数组 ans 中,得到最终答案。
算法情况
-
时间复杂度:O(n + m), 其中 n 和 m 分别为 items1 和 items2 的长度;
-
空间复杂度:O(n + m), 其中 n 和 m 分别为 items1 和 items2 的长度。

代码
class Solution {
public:vector<vector<int>> mergeSimilarItems(vector<vector<int>>& items1, vector<vector<int>>& items2) {// map默认对key升序排序map<int, int> mp;// 转化为mapfor(auto t : items1){mp[t[0]] = t[1];}for(auto t2: items2){mp[t2[0]] += t2[1];}vector<vector<int>> ans;// map 转化为 vector<vector<int>>for(auto s : mp){vector<int> temp = {s.first, s.second};ans.push_back(temp);}return ans;}
};
相关文章:

【LeetCode】2363. 合并相似的物品
2363. 合并相似的物品 题目描述 给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质: items[i] [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,weighti 表示第 i 件物品的 重量 。items 中每…...

华为OD机试题,用 Java 解【出租车计费】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
【人脸识别】DDL:数据分布知识蒸馏思想,提升困难样本(遮挡、低分辨率等)识别效果
论文题目:《Improving Face Recognition from Hard Samples via Distribution Distillation Loss》 论文地址:https://arxiv.org/pdf/2002.03662v3.pdf 代码地址:https://github.com/HuangYG123/DDL 1.前言及相关工作 Large facial variatio…...
如何管理好仓库/库房?
仓库管理是企业管理中不可缺少的一部分,事关企业能否正常运行的关键之一,古人有云:“三军未动粮草先行”,一个企业仓库管理做不好,他的生产管理肯定也是做不好的,不是说生产管理人员的管理能力不具备&#…...

Unity Lighting -- Unity的光源简介
在主菜单栏中,点击Window -> Rendering -> Light Explorer打开光源管理器,这个标签页可以看到场景中所有的光源,包括每个光源的类型,形状,模式,颜色,强度,阴影等信息。 在主菜…...
Android仿网易云音乐歌单详情页
效果图实现思路:1、Activity设置自定义Shared Element切换动画2、透明状态栏(透明Toolbar,使背景图上移)3、Toolbar底部增加和背景一样的高斯模糊图,并上移图片(为了使背景图的底部作为Toolbar的背景)4、上…...

linux基本功系列之free命令实战
文章目录前言一. free命令介绍二. 语法格式及常用选项三. 参考案例3.1 查看free相关的信息3.2 以MB的形式显示内存的使用情况3.3 以总和的形式显示内存的使用情况3.4 周期性的查询内存的使用情况3.5 以更人性化的形式来查看内存的结果输出总结前言 大家好,又见面了…...

华为OD机试模拟题 用 C++ 实现 - 连续子串(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)) 文章目录 最近更新的博客使用说明连续子串题目输入输出示例一输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD …...
【软考——系统架构师】UML 建模与架构文档化
🔎这里是【软考——系统架构师】,关注我考试轻松过线 👍如果对你有帮助,给博主一个免费的点赞以示鼓励 欢迎各位🔎点赞👍评论收藏⭐️ 文章目录UML 基础UML 软件开发过程系统架构文档化送书福利UML 基础 U…...

Spring中常用注解
声明 bean 的注解 Component:泛指各种组件 Controller、Service、Repository 都可以称为Component Controller:控制层 Service:业务层 Repository:数据访问层Bean 的生命周期属性 Scope 设置类型包括:设置 Spring 容器…...
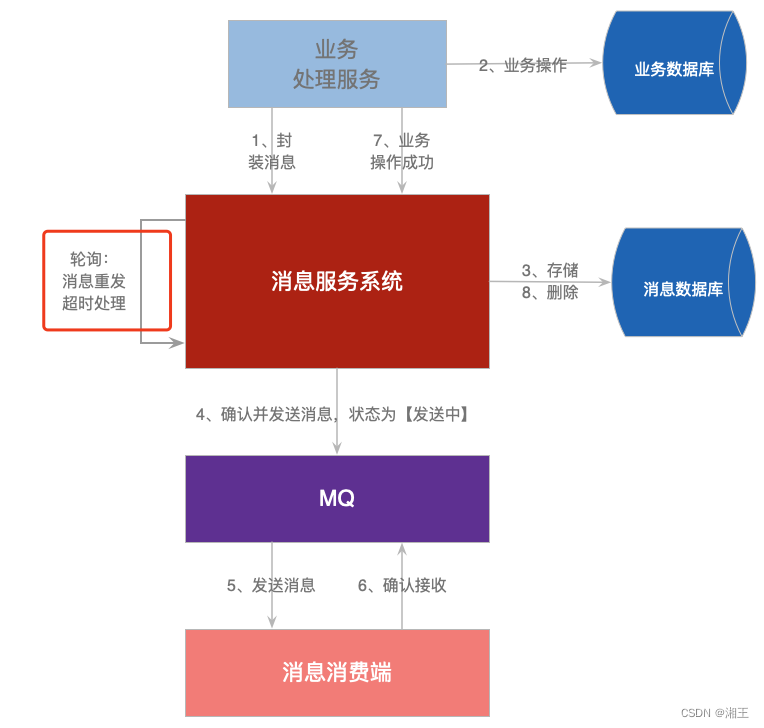
基于SpringCloud的可靠消息最终一致性06:轮询事务消息
上一节把可靠消息最终一致性的正常逻辑代码顺序执行了一次,并且对于同一个事务消息,在正常情况下它要被发送至少两次。 这是因为在发送消息之前,TransactionMessageService就已经把消息保存到了数据库中。而在首次消费完消息后,TransactionMessageListener并没有从数据库中…...

Python Flask + Echarts 轻松制作动态酷炫大屏( 附代码)
目录一、确定需求方案二、整体架构设计三、编码实现 (关键代码)四、完整代码五、运行效果1.动态实时更新数据效果图 说明: 其中 今日抓拍,抓拍总数,预警信息统计,监控点位统计图表 做了动态实时更新处理。 2.静态…...
:SourceMap讲解以及使用)
Wepack(1):SourceMap讲解以及使用
今天我们来讲讲定位源码的工具 Sourcemap , 我们先讲最简单的配置,之后才补充 sourcemap 的其他属性 Sourcemap 作用 可以在打包的代码直接对应相应源码 例如 vue2 , vue3可以把对应的错误上传到相关服务器 使用 webpack.config.js const config …...

华为OD机试题,用 Java 解【最多等和不相交连续子序列】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
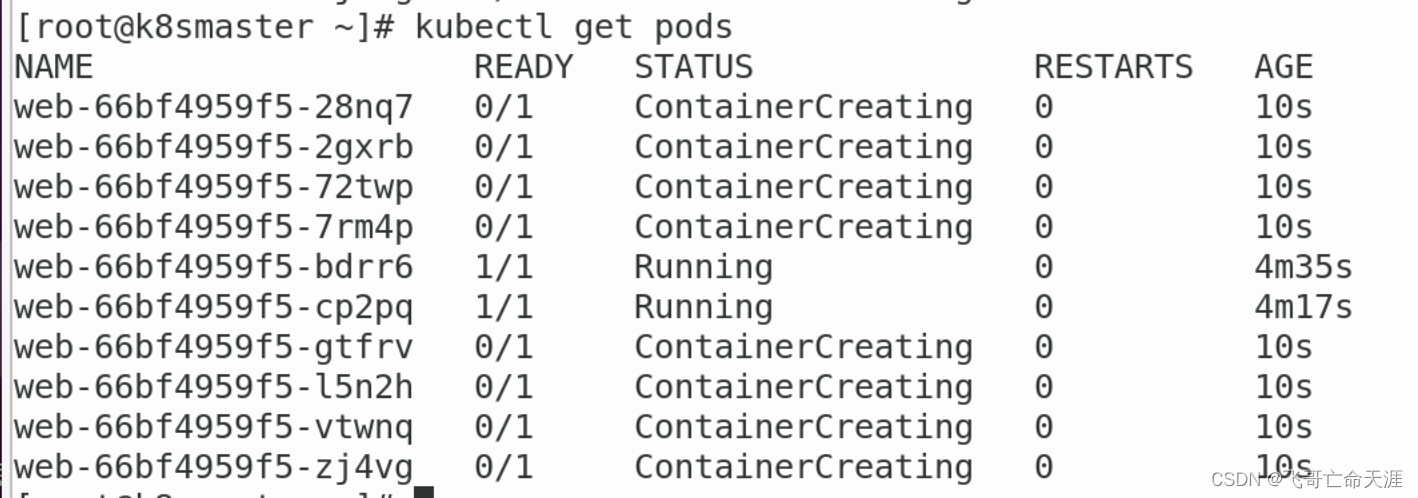
Kubernetes06:Controller
Kubernetes06:Controller 1、什么是controller 管理和运行容器的对象,是一个物理概念 在集群上管理和运行容器的对象 2、Pod和Controller之间的关系 Pod是通过controller来实现应用的运维 比如伸缩、滚动升级等等操作Pod和Controller之间通过 label 标签建立关系…...

采购文件中 RFI、RFQ、RFP、IFB的区别
【PMBOK的描述】 采购文件用于征求潜在卖方的建议书。如果主要依据价格来选择卖方(如购买商业或标准产品时),通常就使用标书、投标或报价等术语。如果主要依据其他考虑(如技术能力或技术方法)来选择卖方࿰…...

linux升级gcc版本详细教程
0.前言一般linux操作系统默认的gcc版本都比较低,例如centos7系统默认的gcc版本为4.8.5。gcc是从4.7版本开始支持C11的,4.8版本对C11新特性的编译支持还不够完善,因此如果需要更好的体验C11以及以上版本的新特性,需要升级gcc到一个…...

NBA Top Shot 跌落神坛
近日,美国职业篮球联盟(NBA)授权的NFT 项目“NBA Top Shot Moments”被纽约法院初步裁定为“可能符合证券的定义”,虽然这不是对2021年用户指控该项目违法的最终判决,但这个裁定引发了市场担忧,部分NFT的地…...
)
状态管理Pinia使用详解(带你入门)
状态管理Pinia使用详解(带你从入门到入神) 序: 如果你之前使用过 vuex 进行状态管理的话,那么 pinia 就是一个类似的插件。它是最新一代的轻量级状态管理插件。你可以通过defineStore来简单创建一个存储管理。 与 vuex 相比,pinia 提…...
Linux系统基础命令(一)
一、图形界面和终端界面 图形界面:是指采用图形方式显示的计算机操作用户界面。 终端界面:是指黑底白字的命令行界面。 什么是tty呢? tty:终端设备的统称。 tty一词源于Teletypes,或者teletypewriters,…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
