Python算法——平衡二叉树(AVL)
Python中的平衡二叉搜索树(AVL树)算法详解
平衡二叉搜索树(AVL树)是一种自平衡的二叉搜索树,它通过在插入或删除节点时进行旋转操作来保持树的平衡性。在AVL树中,任何节点的两个子树的高度差(平衡因子)最多为1。这种平衡性质确保了AVL树的高度始终是对数级别,使得查找、插入和删除等操作的时间复杂度保持在O(log n)。在本文中,我们将深入讨论AVL树的原理,并提供Python代码实现。
AVL树的节点定义
首先,我们定义AVL树的节点类:
class AVLNode:def __init__(self, key):self.key = keyself.height = 1self.left = Noneself.right = None
AVL树的节点除了包含值之外,还记录了节点的高度。这个高度信息是维持平衡的关键。
插入操作
插入操作是在AVL树中插入新节点的过程,同时需要保持树的平衡。插入后,我们需要更新节点的高度,并进行旋转操作来恢复平衡。
def insert(root, key):if root is None:return AVLNode(key)if key < root.key:root.left = insert(root.left, key)elif key > root.key:root.right = insert(root.right, key)# 更新节点的高度root.height = 1 + max(get_height(root.left), get_height(root.right))# 获取平衡因子balance = get_balance(root)# 进行旋转操作来恢复平衡# 左旋if balance > 1 and key < root.left.key:return rotate_right(root)# 右旋if balance < -1 and key > root.right.key:return rotate_left(root)# 左右双旋if balance > 1 and key > root.left.key:root.left = rotate_left(root.left)return rotate_right(root)# 右左双旋if balance < -1 and key < root.right.key:root.right = rotate_right(root.right)return rotate_left(root)return root
删除操作
删除操作是在AVL树中删除节点的过程,同时需要保持树的平衡。删除后,我们需要更新节点的高度,并进行旋转操作来恢复平衡。
def delete(root, key):if root is None:return rootif key < root.key:root.left = delete(root.left, key)elif key > root.key:root.right = delete(root.right, key)else:# 节点有一个或没有子节点if root.left is None:return root.rightelif root.right is None:return root.left# 节点有两个子节点,找到右子树的最小节点root.key = find_min(root.right).key# 删除右子树的最小节点root.right = delete(root.right, root.key)# 更新节点的高度root.height = 1 + max(get_height(root.left), get_height(root.right))# 获取平衡因子balance = get_balance(root)# 进行旋转操作来恢复平衡# 左旋if balance > 1 and get_balance(root.left) >= 0:return rotate_right(root)# 右旋if balance < -1 and get_balance(root.right) <= 0:return rotate_left(root)# 左右双旋if balance > 1 and get_balance(root.left) < 0:root.left = rotate_left(root.left)return rotate_right(root)# 右左双旋if balance < -1 and get_balance(root.right) > 0:root.right = rotate_right(root.right)return rotate_left(root)return root
辅助函数
为了实现插入和删除操作,我们需要一些辅助函数:
def get_height(node):if node is None:return 0return node.heightdef get_balance(node):if node is None:return 0return get_height(node.left) - get_height(node.right)def rotate_left(z):y = z.rightT2 = y.left# 执行左旋y.left = zz.right = T2# 更新节点的高度z.height = 1 + max(get_height(z.left), get_height(z.right))y.height = 1 + max(get_height(y.left), get_height(y.right))return ydef rotate_right(y):x = y.leftT2 = x.right# 执行右旋x.right = yy.left = T2# 更新节点的高度y.height = 1 + max(get_height(y.left), get_height(y.right))x.height = 1 + max(get_height(x.left), get_height(x.right))return x
示例
创建一个AVL树并演示插入和删除操作:
# 创建空树
avl_root = None# 插入操作
keys_to_insert = [50, 30, 70, 20, 40, 60, 80]
for key in keys_to_insert:avl_root = insert(avl_root, key)# 中序遍历查看结果
def inorder_traversal_avl(root):if root is not None:inorder_traversal_avl(root.left)print(f"({root.key}, {get_balance(root)})", end=" ")inorder_traversal_avl(root.right)print("中序遍历结果:", end=" ")
inorder_traversal_avl(avl_root)# 删除操作
delete_key = 30
avl_root = delete(avl_root, delete_key)print("\n删除节点 30 后中序遍历结果:", end=" ")
inorder_traversal_avl(avl_root)
输出结果:
中序遍历结果: (20, 1) (30, 0) (40, 0) (50, -1) (60, 0) (70, 0) (80, 0)
删除节点 30 后中序遍历结果: (20, 1) (40, 0) (50, 0) (60, 0) (70, 0) (80, 0)
这表示插入和删除操作都能够保持AVL树的平衡。AVL树通过自平衡的方式,保证了树的高度始终是对数级别,使得查找、插入和删除等操作的时间复杂度保持在O(log n)。通过理解其原理和实现,您将能够更好地应用AVL树解决实际问题。
相关文章:
)
Python算法——平衡二叉树(AVL)
Python中的平衡二叉搜索树(AVL树)算法详解 平衡二叉搜索树(AVL树)是一种自平衡的二叉搜索树,它通过在插入或删除节点时进行旋转操作来保持树的平衡性。在AVL树中,任何节点的两个子树的高度差(平…...
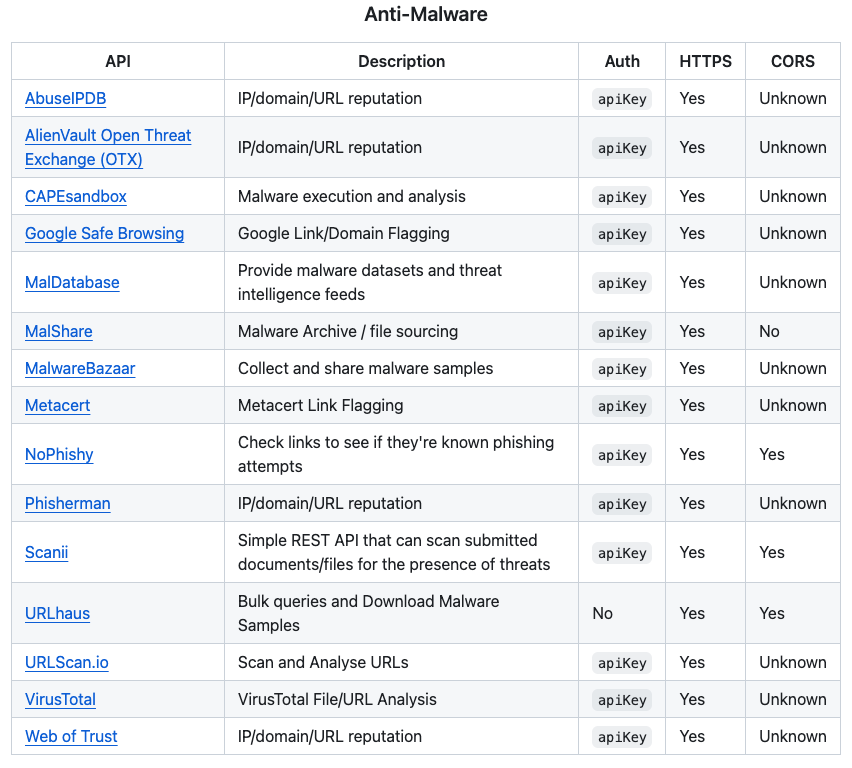
公开可用的API 合集
这是一个开源项目列表,收录了一些公开可用、无需注册或认证即可使用的API接口。 这个项目解决了开发者们在寻找合适的API时遇到的各种困难,如无法快速定位、难以筛选等问题,为他们提供了便捷的一站式查询服务。 项目是“public-apis”&…...

单片机编程原则
多任务编程的概念 方式一:实时操作系统(不建议新手使用) 方式二 :裸机多任务模型 逻辑多任务的基本原理 把三个任务分别分为一个一个的片段 然后先执行任务一的第一个切片 执行第二个任务的第一个片段 执行第三个任务的第一个片…...
开源短剧付费变现小程序源码系统+在线开通会员+在线充值 带完整的搭建教程
说起微短剧,相信大家都不会陌生。相比传统网剧冗长的剧情,微短剧最大的看点,是时长短、高浓缩,顺应了当下用户娱乐时间碎片化趋势。其故事题材多为赘婿、霸道总裁、穿越、重生等看似夸张、无厘头,但却非常“上头”的虚…...

基于Python机器学习、深度学习技术提升气象、海洋、水文领域实践应用能力
Python是功能强大、免费、开源,实现面向对象的编程语言,能够在不同操作系统和平台使用,简洁的语法和解释性语言使其成为理想的脚本语言。除了标准库,还有丰富的第三方库,Python在数据处理、科学计算、数学建模、数据挖…...

电商平台为什么需要及时部署ssl证书?
电商平台为什么需要及时部署ssl证书? 21世纪以来,互联网技术得到了快速的发展和应用上的普及,为生活、工作、学习都带来了巨大的变化。现代社会中,快节奏的生活让人们的购物方式也发生了极大的转变,逐渐由线下转为了线…...
卡码网语言基础课 | 12. 位置互换
通过本次练习,将要学习到以下C知识点: 位置互换交换变量字符串 题目:给定一个长度为偶数位的字符串,请编程实现字符串的奇偶位互换。 奇偶位互换是指字符串的奇数位和偶数位相互交换位置 即:第一位和第二位交换&…...

用DOM来读取XML时要注意的一些概念
2023年11月15日,周三下午 在 DOM(文档对象模型)中,有一些重要的概念和术语: 文档对象(Document Object):表示整个 XML 文档的根节点,它是 DOM 树的入口点。元素节点&…...

openresty安装配置,执行shell脚本
下载并解压 OpenResty 源代码: bashCopy code wget https://openresty.org/download/openresty-1.19.9.1.tar.gz tar -zxvf openresty-1.19.9.1.tar.gz cd openresty-1.19.9.1 运行 ./configure 并指定安装路径: bashCopy code ./configure --prefix…...

解决Dockerfile中 Could not initialize class sun.awt.X11FontManager错误
Dockerfile中增加命令 RUN yum install dejavu-sans-fonts fontconfig -y如果您使用的是基于Alpine Linux的发行版,可以使用apk命令来安装DejaVu Sans字体和fontconfig工具 RUN apk update RUN apk add ttf-dejavu fontconfig...

Kubernetes(k8s)进阶
文章目录 Kubernetes进阶一、Namespace(名称空间)1.namespace介绍2.管理namespace查看namespace创建namespaceyaml文件配置namespace 二、Pod(最小基本部署单元)1.pod介绍2.管理pod创建并运行pod查看pod信息访问pod删除podyaml文件…...

[Vue 配置] Vite + Vue3 项目配置和使用 NProgress
文章归档:https://www.yuque.com/u27599042/coding_star/mfmsrf9tz98ox3qg 安装 pnpm i nprogress配置 NProgress 其他更多可参考,仓库地址:https://github.com/rstacruz/nprogress 在 src/config/nprogress.js 中进行配置 是否展示右上角圆…...

Android MQTT开发之 Hivemq MQTT Client
使用一个开源库:hivemq-mqtt-client,这是Java生态的一个MQTT客户端框架,需要Java 8,Android上使用的话问题不大,需要一些额外的配置,下面列出了相关的配置,尤其是 packagingOptions,…...

【Maven教程】(十一):使用 Maven 构建 Web应用 —— 使用 jetty-maven-plugin 进行测试、使用 Cargo 实现自动化部署~
Maven 使用 Maven 构建 Web应用 1️⃣ Web 项目的目录结构2️⃣ account-service2.1 account-service的 POM2.2 account-service 的主代码 3️⃣ account-web3.1 account-web 的POM3.2 account-web 的主代码 4️⃣ 使用 jetty-maven-plugin 进行测试5️⃣ 使用 Cargo 实现自动…...
番外 2 : LoadRunner 的安装以及配置
LoadRunner 的安装以及配置教程 一 . 配置 IE 浏览器二 . 安装 LoadRunner 工具三 . 修改默认浏览器的配置四 . 设置 LoadRunner 能够获取本地资源 Hello , 大家好 , 又给大家带来新的专栏喽 ~ 这个专栏是专门为零基础小白从 0 到 1 了解软件测试基础理论设计的 , 虽然还不足以…...
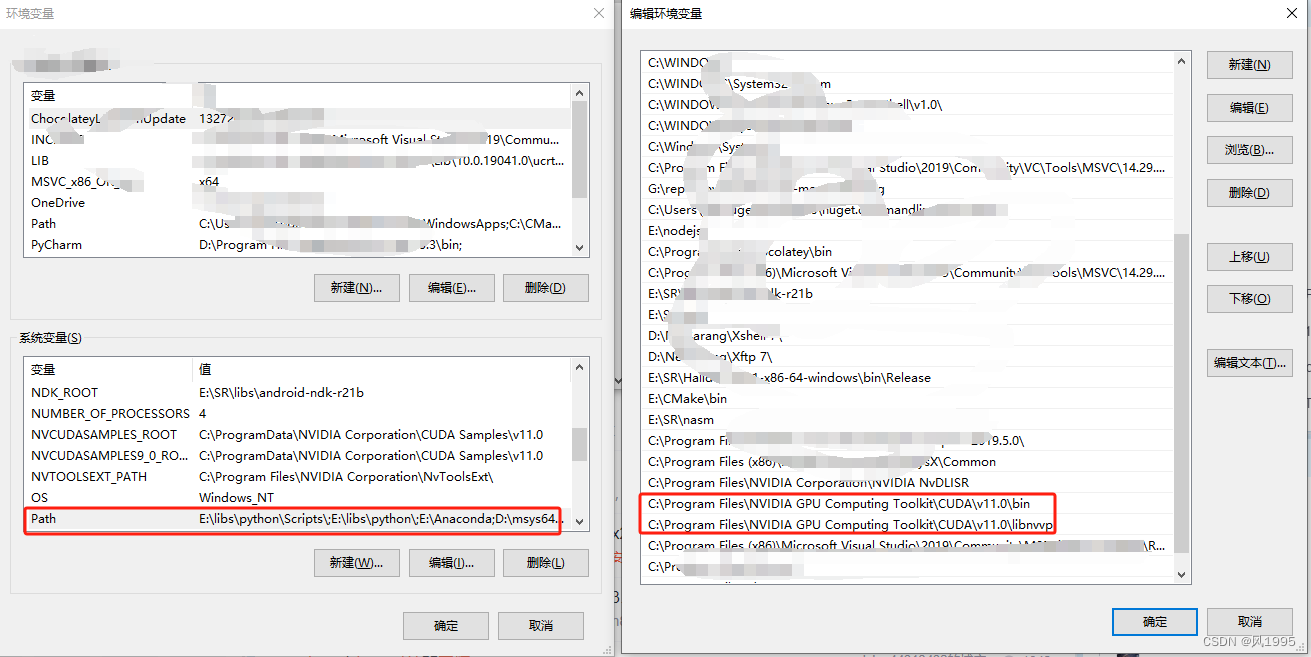
win10正确配置tensorRT环境
目的 使用tensorRT进行网络模型部署,加快推理速度 方法 安装tensorRT的过程需要对各种组件的版本进行匹配 前置安装套件有: 1、CUDA 2、cuDNN 3、pyCUDA 4、tensorflow或pytorch 主要记录tensorRT安装: tensorRT安装配置查询 步骤: 1、去tensorRT官网…...
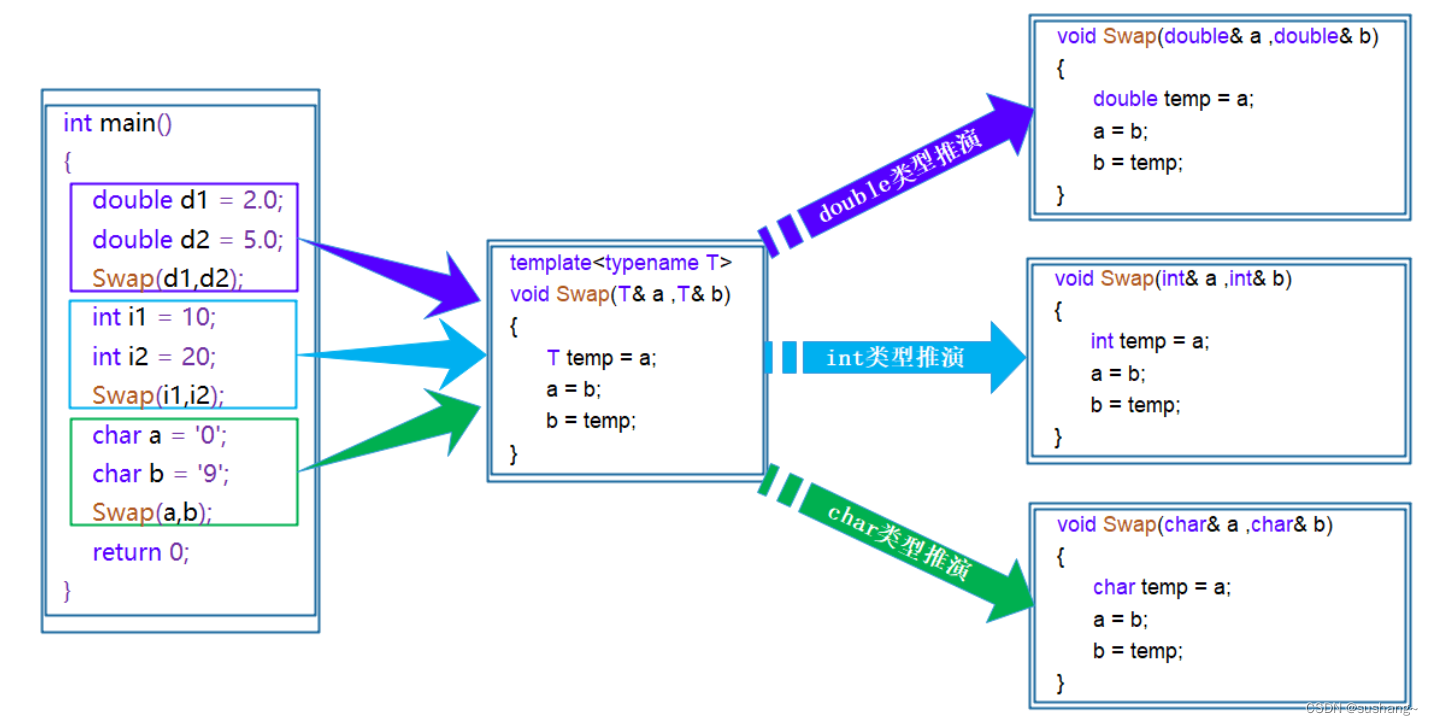
C++初阶-模板初阶
模板初阶 一、泛型编程二、函数模板2.1函数模板概念2.2函数模板格式2.3函数模板的原理2.4函数模板的原理2.5模板参数的匹配原则 三、类模板3.1类模板的定义格式3.2类模板的实例化 一、泛型编程 如何实现一个通用的交换函数呢? void Swap(int& left, int& …...
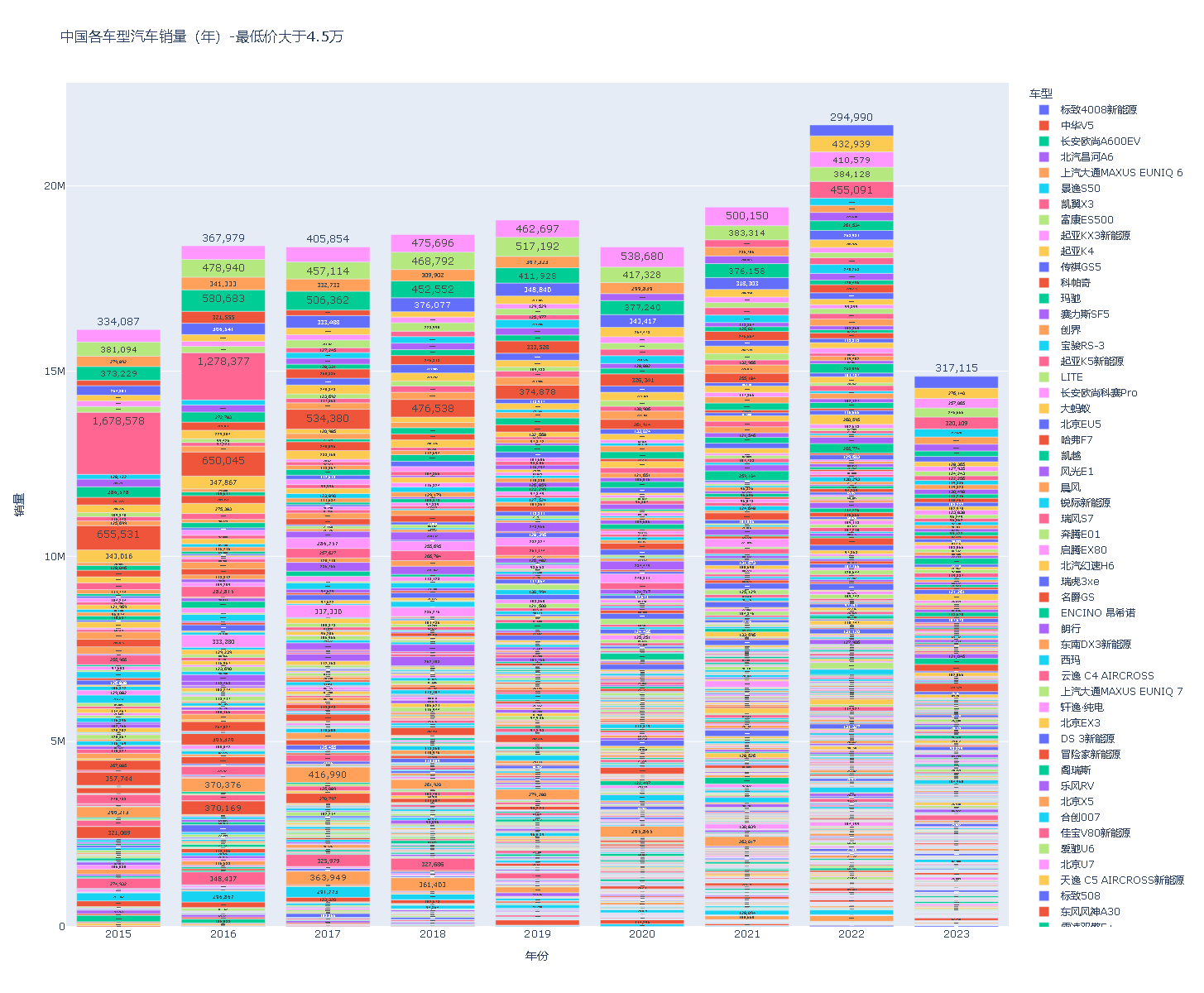
基于Python实现汽车销售数据可视化【500010086】
导入模块 import numpy as np import pandas as pd import plotly.graph_objects as go import plotly.express as px获取数据 df1 pd.read_excel(r"./data/中国汽车总体销量.xlsx") print(df1.head(5))df1.info()df1[年份] df1[时间].dt.year df1[月份] df1[时…...
 卡住超时导致报错)
dist.init_process_group() 卡住超时导致报错
在跑模型是遇到一个问题: import torch.distributed as dist dist.init_process_group(backend"nccl", init_methodtcp://localhost:%d % tcp_port, ranklocal_rank, world_sizenum_gpus)程序卡在这一步一动不动。. 解决办法一: 我看网上有人…...

RESTFul API:真是让人又爱又恨
RESTFul API是一种广泛使用的Web服务设计风格,它以资源为中心,通过HTTP方法来操作这些资源。然而,尽管RESTFul架构风格在许多情况下都非常有用,但在实际应用中,我们也发现了一些不足之处。本文将详细阐述这些问题&…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
