代码随想录算法训练营Day 53 || 1143.最长公共子序列、1035.不相交的线、53. 最大子序和
1143.最长公共子序列
力扣题目链接
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
示例 1:
- 输入:text1 = "abcde", text2 = "ace"
- 输出:3
- 解释:最长公共子序列是 "ace",它的长度为 3。
示例 2:
- 输入:text1 = "abc", text2 = "abc"
- 输出:3
- 解释:最长公共子序列是 "abc",它的长度为 3。
示例 3:
- 输入:text1 = "abc", text2 = "def"
- 输出:0
- 解释:两个字符串没有公共子序列,返回 0。
提示:
- 1 <= text1.length <= 1000
- 1 <= text2.length <= 1000 输入的字符串只含有小写英文字符。
思路
-
定义状态:创建一个二维数组
dp,其中dp[i][j]表示text1的前i个字符和text2的前j个字符的最长公共子序列的长度。 -
状态转移:
- 如果
text1[i-1] == text2[j-1],则dp[i][j] = dp[i-1][j-1] + 1; - 否则,
dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
- 如果
-
初始化:
dp[0][j]和dp[i][0]都应初始化为 0,因为空字符串与任何字符串的最长公共子序列长度都是 0。 -
填充表格:按行或按列填充整个
dp表格。 -
返回结果:
dp[text1.length][text2.length]就是最长公共子序列的长度。
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:m, n = len(text1), len(text2)dp = [[0] * (n + 1) for _ in range(m + 1)]for i in range(1, m + 1):for j in range(1, n + 1):if text1[i - 1] == text2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[m][n]
1035.不相交的线
力扣题目链接
我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。
现在,我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且我们绘制的直线不与任何其他连线(非水平线)相交。
以这种方法绘制线条,并返回我们可以绘制的最大连线数。

思路
-
定义状态:创建一个二维数组
dp,其中dp[i][j]表示数组A的前i个元素和数组B的前j个元素可以形成的最大连线数。 -
状态转移:
- 如果
A[i-1] == B[j-1],则可以在这两个元素之间绘制一条线,因此dp[i][j] = dp[i-1][j-1] + 1; - 否则,不能在
A[i-1]和B[j-1]之间绘制线,所以dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
- 如果
-
初始化:
dp[0][j]和dp[i][0]都应初始化为 0,因为当任一数组为空时,最大连线数为 0。 -
填充表格:按行或按列顺序填充
dp表格。 -
返回结果:
dp[A的长度][B的长度]就是可以绘制的最大连线数。
class Solution:def maxUncrossedLines(self, A: List[int], B: List[int]) -> int:m, n = len(A), len(B)dp = [[0] * (n + 1) for _ in range(m + 1)]for i in range(1, m + 1):for j in range(1, n + 1):if A[i - 1] == B[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[m][n]
53. 最大子序和
力扣题目链接(opens new window)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
- 输出: 6
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
思路
-
定义状态:创建一个数组
dp,其中dp[i]表示以nums[i]结尾的最大子序和。 -
状态转移:对于每个
i,有两种情况:- 把
nums[i]加入前面的子数组中,这种情况下最大子序和是dp[i-1] + nums[i]; - 从
nums[i]开始一个新的子数组,这种情况下最大子序和是nums[i]自己。 因此,dp[i] = max(dp[i-1] + nums[i], nums[i])。
- 把
-
初始化:
dp[0]应该初始化为nums[0],因为最开始的最大子序和就是数组的第一个元素。 -
结果:遍历
dp数组,找出最大值,即为最大子序和。
class Solution:def maxSubArray(self, nums: List[int]) -> int:n = len(nums)dp = nums.copy()for i in range(1, n):dp[i] = max(dp[i - 1] + nums[i], nums[i])return max(dp)
相关文章:

代码随想录算法训练营Day 53 || 1143.最长公共子序列、1035.不相交的线、53. 最大子序和
1143.最长公共子序列 力扣题目链接 给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何…...

Oracle JDBC数据库驱动程序介绍
Maven Central上所有Oracle JDBC数据库驱动程序 现在不仅可以在Maven Central上使用甲骨文数据库最新版本,而且还可以获得所有受支持的Oracle JDBC驱动程序发行版,包括19.3.0.0、18.3.0.0、12.2.0.1和11.2.0.4。从现在开始,Maven Central确实…...

scipy实现单因素方差分析
经典例题 某校高二年级共有四个班,采用四种不同的教学方法进行数学教学,为了比较这四种教学法的效果是否存在明显的差异,期末统考后,从这四个班中各抽取 5 名考生的成绩,如下所示。 班级 一班 二班 三班 四班 …...
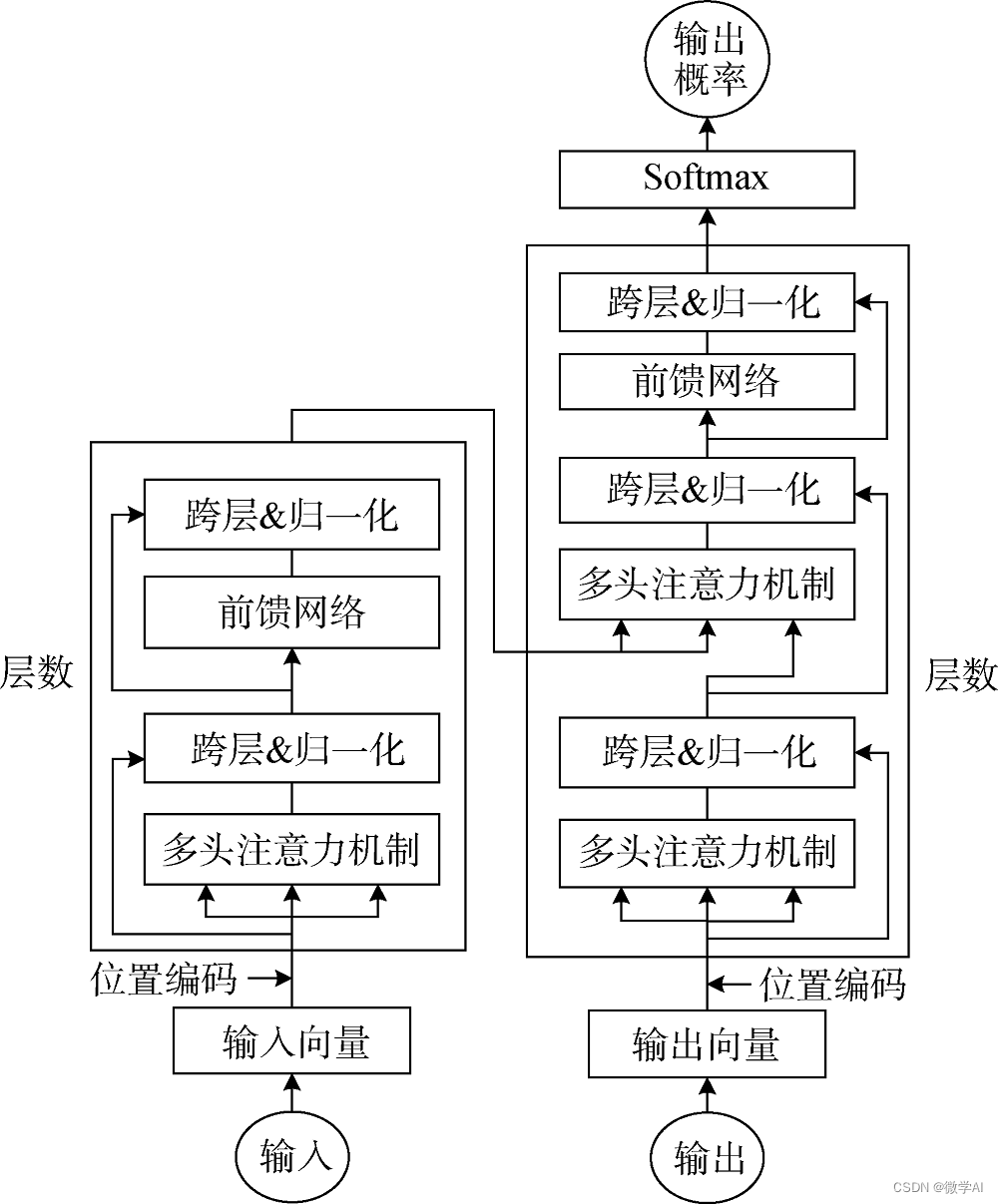
深度学习实战59-NLP最核心的模型:transformer的搭建与训练过程详解,手把手搭建与跑通
大家好,我是微学AI,今天给大家介绍一下深度学习实战59-NLP最核心的模型:transformer的搭建与训练过程详解,手把手搭建与跑通。transformer是一种基于自注意力机制的深度学习模型,由Vaswani等人在2017年的论文《Attention is All You Need》中提出。它最初被设计用来处理序…...
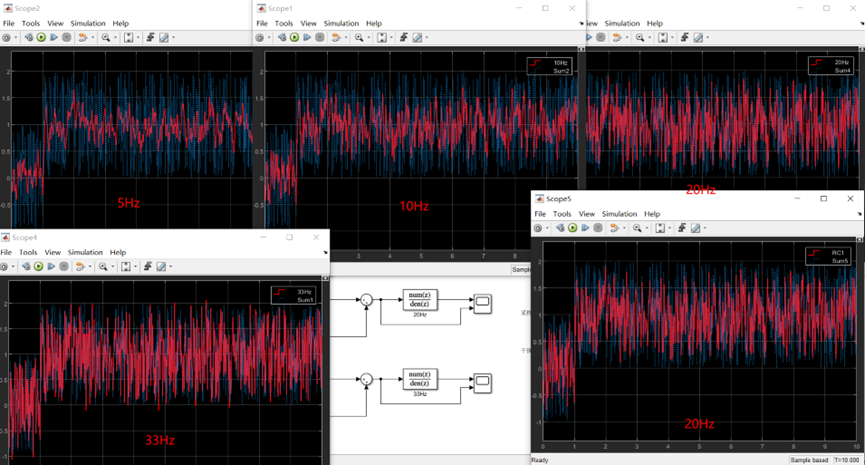
一阶滤波器(一阶巴特沃斯滤波器)
连续传递函数G(s) 离散传递函数G(z) 转换为差分方程形式 一阶巴特沃斯滤波器Filter Designer参数设计:参考之前的博客Matlab的Filter Designer工具设计二阶低通滤波器 设计采样频率100Hz,截止频率20Hz。 注意:设计参数使用在离散系统中&…...
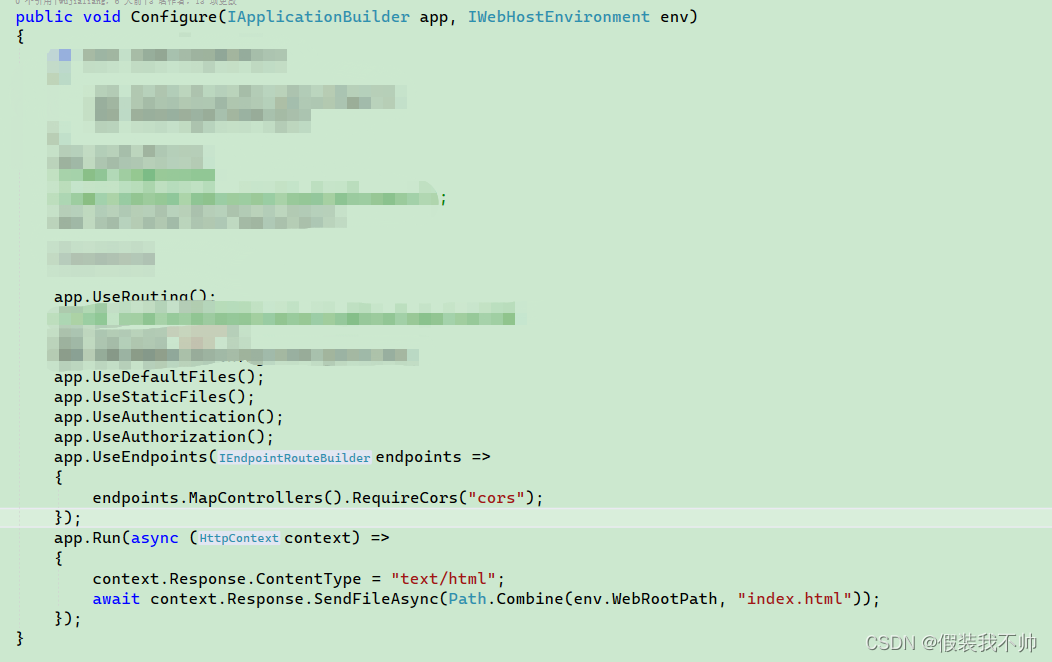
.net core中前端vue HTML5 History 刷新页面404问题
放到启动的应用程序的最后面 app.Run(async (context) > {context.Response.ContentType "text/html";await context.Response.SendFileAsync(Path.Combine(env.WebRootPath, "index.html")); });https://blog.csdn.net/lee576/article/details/88355…...
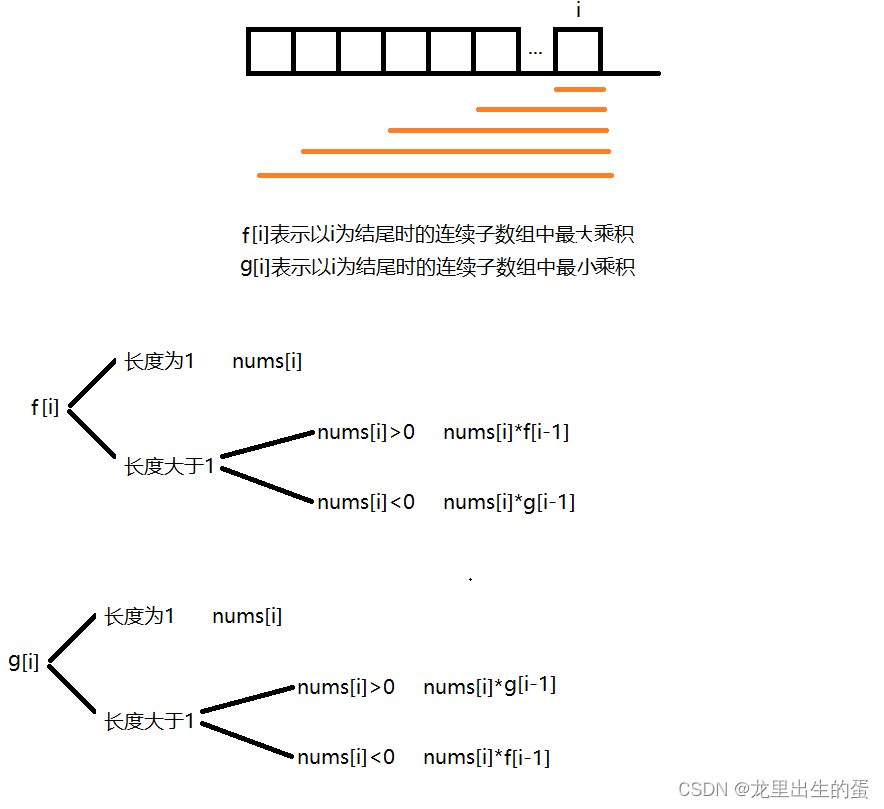
【152.乘积最大子数组】
目录 一、题目描述二、算法原理三、代码实现 一、题目描述 二、算法原理 三、代码实现 class Solution { public:int maxProduct(vector<int>& nums) {int nnums.size();vector<int> f(n);vector<int> g(n);f[0]g[0]nums[0];int retnums[0];for(int i1;…...

如何开发OA系统场景的系统架构
1.开发OA系统场景的系统架构 针对开发OA系统的场景,以下是一个简单的系统架构示例,包括前端、后端和数据库三个基本部分: 前端: 使用React框架进行前端开发,构建用户界面和交互逻辑。前端模块包括日程管理模块、文档管…...

spring boot 集成 RedisSearch 和 RedisJSON
1. 准备工作 环境说明 java 8;redis7.2.2,redis集成RedisSearch、redisJson 模块;spring boot 2.5在执行 redis 命令, 或者监控 程序执行的redis 指令时,可以采用 redisinsight查看,下载地址。 背景说明 需…...

【Kotlin精简】第8章 协程
1 简介 Kotlin 中的协程提供了一种全新处理并发的方式,您可以在 Android 平台上使用它来简化异步执行的代码。协程是从 Kotlin 1.3 版本开始引入,但这一概念在编程世界诞生的黎明之际就有了,最早使用协程的编程语言可以追溯到 1967 年的 Sim…...
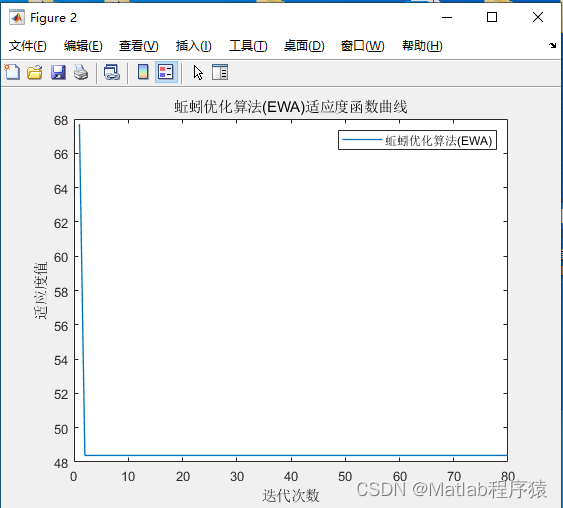
【MATLAB源码-第79期】基于蚯蚓优化算法(EOA)的栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 蚯蚓优化算法(Earthworm Optimisation Algorithm, EOA)是一种启发式算法,灵感来源于蚯蚓在自然界中的行为模式。蚯蚓优化算法主要模仿了蚯蚓在寻找食物和逃避天敌时的行为策略。以下是蚯蚓…...

RPC实现简单解析
RPC是什么,先摘取一段解释: RPC全称为远程过程调用(Remote Procedure Call),它是一种计算机通信协议,允许一个计算机程序调用另一个计算机上的子程序,而无需了解底层网络细节。通过RPCÿ…...

【Ubuntu】Ubuntu20.04下安装视频播放器vlc和录屏软件ssr
【Ubuntu】Ubuntu20.04下安装视频播放器vlc和录屏软件ssr 文章目录 【Ubuntu】Ubuntu20.04下安装视频播放器vlc和录屏软件ssr1. 安装视频播放器vlc2. 安装录屏软件ssr 1. 安装视频播放器vlc sudo apt-get install vlcvlc是一款比较简洁的视频播放器,如下所示 2. 安…...
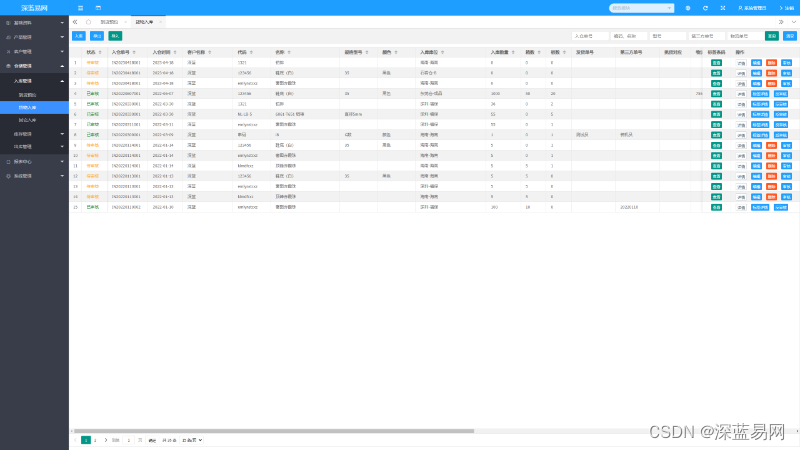
WMS仓储管理系统与TMS系统整合后的优势
随着全球化的加速和供应链网络的日益复杂,仓库和运输成为企业运营中的两个关键环节。为了更高效地管理这两个环节,许多企业开始探索将WMS仓储管理系统和TMS运输管理系统整合的可能性。这种整合不仅可以提升仓库流程的可见性,还有助于改善调度…...

测试的专用
测试...
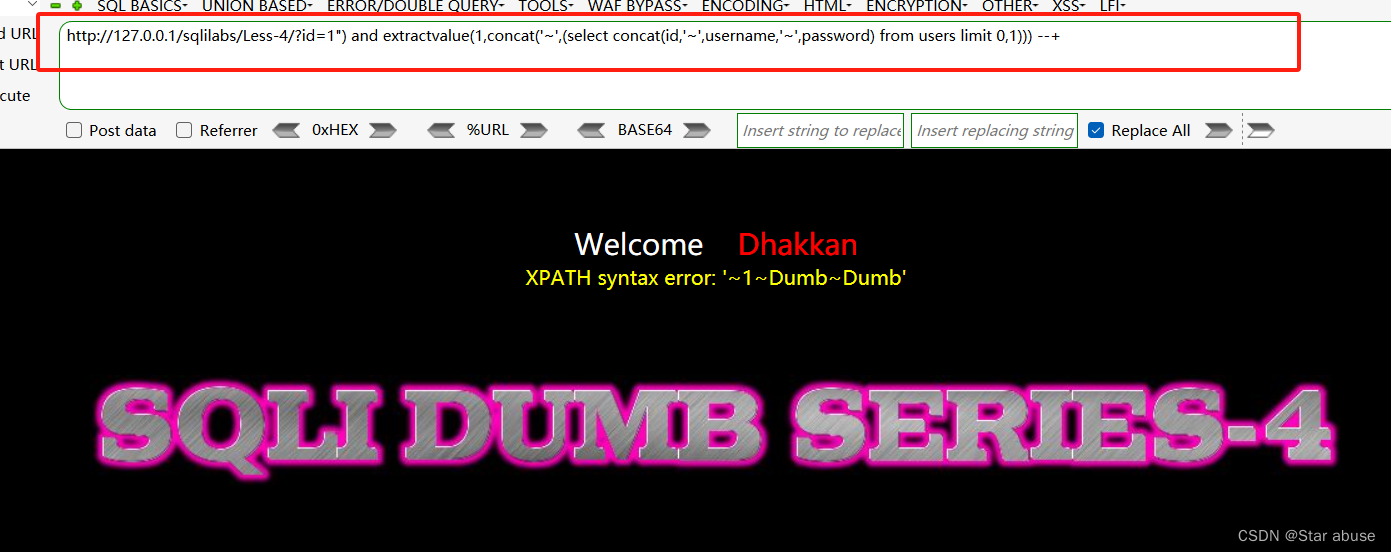
sqli-labs(Less-4) extractvalue闯关
extractvalue() - Xpath类型函数 1. 确认注入点如何闭合的方式 2. 爆出当前数据库的库名 http://127.0.0.1/sqlilabs/Less-4/?id1") and extractvalue(1,concat(~,(select database()))) --3. 爆出当前数据库的表名 http://127.0.0.1/sqlilabs/Less-4/?id1") …...
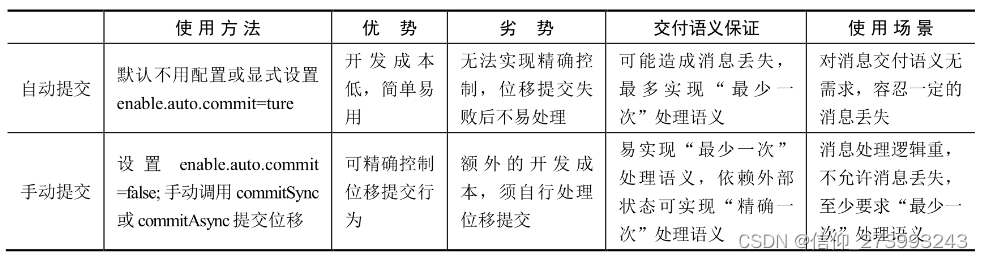
Kafka简单汇总
Kafka的结构图 多个Parttion共同组成这个topic的所有消息。每个consumer都属于一个consumer group,每条消息只能被consumer group中的一个Consumer消费, 但可以被多个consumer group消费。即组间数据是共享的,组内数据是竞争的。二、消费模型…...

任务交给谁?委派模式告诉你最佳选择!
文章目录 一、概念二、角色三、代码实现四、委派模式在源码中的体现五、委派模式的优缺点优点缺点 一、概念 委派模式(Delegate Pattern)又叫委托模式,是一种面向对象的设计模式。委派模式是一种行为模式,不属于GOF23种设计模式之中基本作用…...

【JavaEE】Servlet(创建Maven、引入依赖、创建目录、编写及打包、部署和验证、smart Tomcat)
一、什么是Servlet? Servlet 是一种实现动态页面的技术. 是一组 Tomcat 提供给程序猿的 API, 帮助程序猿简单高效的开发一个 web app 1.1 Servlet能干什么? 🚕允许程序猿注册一个类, 在 Tomcat 收到某个特定的 HTTP 请求的时候, 执行这个类…...
降低城市内涝风险,万宾科技内涝积水监测仪的作用
频繁的内涝会削弱和损坏城市的关键基础设施,包括道路、桥梁和公用设施。城市内涝风险降低可以减少交通中断事件,也可以保护居民安全并降低路面维修等成本,进一步确保城市基本服务继续发挥作用。对城市可持续发展来讲有效减少内涝的风险是重要…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
