【L2GD】: 无环局部梯度下降
文章链接:Federated Learning of a Mixture of Global and Local Models
发表期刊(会议): ICLR 2021 Conference(机器学习顶会)
往期博客:FLMix: 联邦学习新范式——局部和全局的结合
目录
- 1.背景介绍
- 2. 梯度下降 GD
- SGD
- LGD
- 3. L2GD
- L2GD创设
- 局部GD和平均局部模型
- L2GD 通信
- L2GD收敛证明
- L2SGD+
1.背景介绍
本文提出了一种新的训练联邦学习模型的优化公式。标准FL旨在从存储在所有参与设备上的私人数据中找到一个单一的全局模型。相比之下,新方法寻求全局模型和局部模型之间的权衡,每个设备可以从自己的私有数据中学习而无需通信。
本文开发了有效的随机梯度下降(SGD)变体来求解新公式,并证明了通信复杂性的保证。该工作的主要贡献包括结合全局和局部模型的FL新范式、新范式的理论性质、无环路局部梯度下降(L2GD)、L2GD的收敛理论以及对局部步骤在联邦学习中的作用的见解。该文件还强调了本地SGD在通信复杂性和个性化联邦学习的好处方面优于传统SGD的潜力。
2. 梯度下降 GD
梯度下降(Gradient Descent,GD)是一种常用的优化算法,用于最小化损失函数或目标函数。基本思想是通过迭代更新模型参数的方式来寻找使目标函数达到最小值的参数值。
GD通过沿着损失函数的负梯度方向来更新模型参数,以减少损失并使模型更符合训练数据。
GD基本步骤:
- 初始化参数:选择初始的模型参数值,随机初始化或根据先验知识设置。
- 计算梯度:在当前参数值处,计算目标函数关于参数的梯度(即目标函数对参数的偏导数)。梯度表示了目标函数在当前参数值处的变化方向和速率。
- 更新参数:根据梯度信息和学习率(learning rate),更新模型参数。学习率决定了每次迭代中参数更新的步长大小。更新规则通常如下所示:
新参数=旧参数−学习率×梯度- 重复迭代:重复步骤 2 和步骤 3,直到满足停止条件,例如达到最大迭代次数、损失函数收敛等。
学习率是一个很重要的超参,制着在每次迭代中更新参数的幅度。它决定了在梯度方向上参数更新的步长大小。
学习率过大可能导致参数更新过大,甚至可能使得优化算法无法收敛,造成震荡或发散。这种情况下,即使损失函数值在短时间内降低,最终可能错过最优解。
学习率过小则可能导致收敛速度缓慢,需要更多的迭代次数才能达到一个较好的解,特别是在损失函数的优化路径中存在较为平缓的部分时。
SGD
随机梯度下降(Stochastic Gradient Descent,SGD)是一种常用的优化算法,用于训练ML模型,特别是在大规模数据集上。它是GD算法的一种变体,使用单个样本或样本小批次(mini-batch)的梯度估计来进行参数更新,而不是使用整个训练集的梯度。这种随机性使得随机梯度下降在大型数据集上更具效率,并且能够更快地收敛到局部最优解。
优点:
- 在大规模数据集上的训练更加高效
- 易于实现
缺点:
- 可能陷入局部最优解
- 对学习率敏感
function stochastic_gradient_descent(data, learning_rate, num_epochs):initialize random parameters thetafor epoch in range(num_epochs):shuffle(data) # Shuffle the data for randomnessfor example in data:input_x, target_y = example# 计算损失函数梯度值 gradient = compute_gradient(input_x, target_y, theta)# 使用梯度下降更新参数for param in theta:param -= learning_rate * gradient[param]return theta
LGD
分层梯度下降(Layer-wise Gradient Descent,LGD)是一种用于深度学习中神经网络训练的优化算法。它的主要思想是将神经网络分层,然后对每一层分别进行训练和更新。这种方法旨在解决深度神经网络训练中的梯度消失或梯度爆炸等问题,并提高网络训练的效率。
与SGD的比较
| SGD | LGD | |
|---|---|---|
| 分层更新 | 每次迭代中使用整个网络的梯度来更新参数 | 对每一层单独计算和更新梯度 |
| 更新频率 | 每次迭代中更新整个网络的参数 | 按层级顺序逐层更新参数,网络参数的更新频率较低 |
| 梯度传播 | 传播通过所有层来更新参数 容易出现梯度消失或梯度爆炸 | 通过分层的方式减少了参数更新时的梯度传播距离 有助于缓解梯度问题 |
| 收敛速度 | 由于同时更新所有参数 需要较长时间才能收敛到较优解 | 通过分层更新 会更快地收敛到局部最优解 |
function layer_wise_gradient_descent(network, data, learning_rate, num_epochs):initialize random parameters for each layer in networkfor epoch in range(num_epochs):shuffle(data) # Shuffle the data for randomnessfor example in data:input_x, target_y = example# Forward pass through the networkpredictions = network.forward_pass(input_x)# Backward pass to compute gradients for each layernetwork.compute_gradients(input_x, target_y)# Update parameters of each layer using gradientsfor layer in network.layers:layer.update_parameters(learning_rate)return network
3. L2GD
文章提出了联邦学习新范式 ♣ \clubsuit ♣ 如下:
♣ min x 1 , . . . , x n ∈ R d { F ( x ) : = f ( x ) + λ ψ ( x ) } f ( x ) : = 1 n ∑ i = 1 n f i ( x i ) ψ ( x ) : = 1 2 n ∑ i = 1 n ∥ x i − x ‾ ∥ 2 \clubsuit \quad \min_{x_1,...,x_n \in \mathbb{R}^d } \{ F(x): = f(x)+ \lambda \psi (x)\} \\ f(x):=\frac{1}{n}\sum_{i=1}^{n} f_i(x_i) \\ \psi (x) := \frac{1}{2n}\sum_{i=1}^{n} \left \| x_i-\overline{x} \right \| ^2 ♣x1,...,xn∈Rdmin{F(x):=f(x)+λψ(x)}f(x):=n1i=1∑nfi(xi)ψ(x):=2n1i=1∑n∥xi−x∥2 其中 λ ≥ 0 \lambda \ge0 λ≥0 是一个惩罚超参, x 1 , . . . , x n ∈ R d x_1,...,x_n \in \mathbb{R}^d x1,...,xn∈Rd 是本地模型参数 , x : = ( x 1 , x 2 , . . . , x n ) ∈ R n d x:=(x_1,x_2,...,x_n) \in\mathbb{R}^{nd} x:=(x1,x2,...,xn)∈Rnd 并且 x ‾ : = 1 n ∑ i = 1 n x i \overline{x}:=\frac{1}{n}\sum_{i=1}^{n}x_i x:=n1∑i=1nxi 是所有本地模型的平均值。
本文设计了一种新的随机化方法Loopless Local GD (L2GD)来求解范式 ♣ \clubsuit ♣
L2GD创设
L2GD方法是一个非一致的SDG,可以视为一个2元和问题,通过随机采样 ∇ f \nabla f ∇f 或者 ∇ ψ \nabla \psi ∇ψ 来估计 ∇ F \nabla F ∇F。
令采样概率为 P ∈ ( 0 , 1 ) P \in(0,1) P∈(0,1),对于 F F F 在 x ∈ R n d x \in \mathbb{R}^{nd} x∈Rnd 的随机梯度可表示为: G ( x ) : = { ∇ f ( x ) 1 − p w i t h p r o b a b i l i t y 1 − p λ ∇ ψ ( x ) p w i t h p r o b a b i l i t y p G(x): = \begin{cases} \frac{\nabla f(x)}{1-p} & with\quad probability \quad 1 − p \\ \frac{\lambda \nabla \psi(x)}{p} & with\quad probability\quad p \\ \end{cases} G(x):={1−p∇f(x)pλ∇ψ(x)withprobability1−pwithprobabilityp其中 G ( x ) G(x) G(x) 是 ∇ F ( x ) \nabla F(x) ∇F(x) 的无偏估计。
使用L2GD以最小化 F F F : ♠ x k + 1 = x k − α ⋅ G ( x k ) \spadesuit \quad x^{k+1}=x^k-\alpha \cdot G(x^k) ♠xk+1=xk−α⋅G(xk) α \alpha α 为学习率或步长,将 G ( x ) G(x) G(x) 代入 ♠ \spadesuit ♠ 可以得到L2GD的更新算法:

在每一轮迭代中,会先抛一枚硬币 ξ \xi ξ :
-
如果 ξ = 1 \xi =1 ξ=1 则以概率 p \quad p \quad p 采样 ∇ ψ \nabla \psi ∇ψ 来估计 ∇ F \nabla F ∇F 并进行参数更新,此时 Master 将每个局部模型向平均值方向移动;
-
如果 ξ = 0 \xi =0 ξ=0 则以概率 1 − p 1-p 1−p 采样 ∇ f \nabla f ∇f 来估计 ∇ F \nabla F ∇F 并进行参数更新,此时所有设备执行一个局部GD步骤。
为了保证 ♡ x i k + 1 = ( 1 − α λ n p ) x i k + α λ n p x ˉ k \heartsuit \quad x^{k+1}_i=(1-\frac{\alpha \lambda}{np})x^k_i+\frac{\alpha \lambda}{np} \bar{x}^k ♡xik+1=(1−npαλ)xik+npαλxˉk 是一个关于 x i k x^k_i xik 和 x ˉ k \bar{x}^k xˉk 的凸组合,
需要对 α \alpha α 的大小进行限制,使 α λ n p < 1 2 \frac{\alpha \lambda}{np}<\frac{1}{2} npαλ<21。
在上述算法的基础上,只需要在连续两次投掷硬币得到不同 ξ \xi ξ 值时进行通信。
需要注意的是,算法语句没有考虑到数据的隐私。 而隐私是FL的一个非常重要的方面。
局部GD和平均局部模型
局部模型的平均值在聚合步骤中不会更改。具体表现为聚合后的 x ˉ k + 1 \bar{x}^{k+1} xˉk+1 具有以下性质(结合公式 ♡ \heartsuit ♡):
x ˉ k + 1 = 1 n ∑ i = 1 n x i k + 1 = 1 n ∑ i = 1 n [ ( 1 − α λ n p ) x i k + α λ n p x ˉ k ] = x ˉ k \bar{x}^{k+1}=\frac{1}{n} \sum_{i=1}^{n} x^{k+1}_i =\frac{1}{n}\sum_{i=1}^{n}[(1-\frac{\alpha \lambda}{np})x^k_i+\frac{\alpha \lambda}{np} \bar{x}^k]=\bar{x}^{k} xˉk+1=n1i=1∑nxik+1=n1i=1∑n[(1−npαλ)xik+npαλxˉk]=xˉk这意味着如果在一个执行序列中发生了几个平均步骤, ♡ \heartsuit ♡ 中的点 a = x ˉ k a=\bar{x}^k a=xˉk 始终保持不变,每个局部模型 x i k x_i^k xik 只是在执行序列和 a a a 的开始处沿着连接局部模型初始值的直线移动,每一步都将 x i k x^k_i xik 向平均值 a 靠近。
至此,我们可以得到这样一个结论:
- 局部GD步骤越多,局部模型越接近纯局部模型
- 采取的平均步骤越多,局部模型就越接近它们的平均值。
局部GD与平均步骤的相对数量由参数 p p p 控制:
- 局部GD步骤的期望数量是 1 p \frac{1}{p} p1
- 平均步骤的期望数量是 1 1 − p \frac{1}{1-p} 1−p1
L2GD 通信

为了更好地理解算法中通信发生的时间,考虑以下可能的抛硬币顺序 :0,0,1,0,1,1,0。
-
前两次抛硬币 ( ξ = 0 ) (\xi =0) (ξ=0) 将导致在所有设备上执行两个局部GD步骤,第 i i i 台设备 的局部模型为 x i k = 2 x_i^{k=2} xik=2;
-
第三次掷硬币 ( ξ = 1 ) (\xi =1) (ξ=1),此时所有的局部模型 x i k = 2 x_i^{k=2} xik=2 都会被传送给 Master,取平均值形成 x ˉ k = 2 \bar{x}^{k=2} xˉk=2,然后就开始了取平均的步骤 ♡ \heartsuit ♡ 得到每台设备的新局部模型 x i k = 3 x_i^{k=3} xik=3
-
第四次掷硬币 ( ξ = 0 ) (\xi =0) (ξ=0),此时 Master 将更新的局部模型 x i k = 3 x_i^{k=3} xik=3 发送回设备 i i i,设备 i i i 随后执行一个局部GD步骤,得到 x i k = 4 x_i^{k=4} xik=4
-
然后是连续三次抛硬币 ( ξ = 1 ) (\xi =1) (ξ=1),这意味着局部模型再次被传递给 Master ,Master 执行三个平均步骤 ♡ \heartsuit ♡ 得到 x i k = 7 x_i^{k=7} xik=7
-
第八次掷硬币 ( ξ = 0 ) (\xi =0) (ξ=0),这使得 Master 将更新后的局部模型 x i k = 7 x_i^{k=7} xik=7 发送回设备 i i i,设备随后执行单个局部GD步骤,得到 x i k = 8 x_i^{k=8} xik=8。
这个例子说明了当两个连续的硬币投掷出不同的值时,需要进行通信:
- 如果0后面跟着一个1,那么所有的设备都与 Master 通信;
- 如果1后面跟着一个0,那么 Master 就返回给设备通信。
- 标准是将每对通信,Device→Master 和随后的 Master → Device,计数为单个通信轮。
- 在
L2GD的 k k k 个迭代中,预期的通信轮数为 p ( 1 − p ) k p(1−p)k p(1−p)k 。
L2GD收敛证明
本文在提出联邦学习新范式的时候做过一个重要的假设,可以参考前文:FLMix: 联邦学习新范式——局部和全局的结合。
对于每一个设备 i i i ,它的目标函数 f i : R d → R f_i:\mathbb{R}^d \rightarrow \mathbb{R} fi:Rd→R 是 L − s m o o t h L-smooth L−smooth 并且 μ − s t r o n g l y \mu -strongly μ−strongly 的凸函数。
用数学表示即为: L f : = L n L_f:=\frac{L}{n} Lf:=nL和 μ f : = μ n \mu_f:=\frac{\mu}{n} μf:=nμ 那么对于函数 ψ \psi ψ ,显然它是凸的。并且有一下表达: ( ∇ ψ ( x ) ) i = 1 n ( x i − x ˉ ) ψ ( x ) = n 2 ∑ i = 1 n ∣ ∣ ( ( ∇ ψ ( x ) ) i ) ∣ ∣ 2 = n 2 ∣ ∣ ∇ ψ ( x ) ∣ ∣ 2 (\nabla \psi(x))_i=\frac{1}{n}(x_i-\bar{x}) \\ \psi(x)=\frac{n}{2}\sum_{i=1}^{n}||((\nabla \psi(x))_i)|| ^2=\frac{n}{2}||\nabla \psi(x)||^2 (∇ψ(x))i=n1(xi−xˉ)ψ(x)=2ni=1∑n∣∣((∇ψ(x))i)∣∣2=2n∣∣∇ψ(x)∣∣2我们保持这个假设在L2DG的计算中仍然成立。
如果 学习率 α < 1 2 L \alpha<\frac{1}{2\mathcal{L} } α<2L1 其中 L : = 1 n max { L 1 − p , λ p } \mathcal{L} :=\frac{1}{n}\max\{\frac{L}{1-p},\frac{\lambda}{p}\} L:=n1max{1−pL,pλ} 有: E [ ∥ x k − x ( λ ) ∥ 2 ] ≤ ( 1 − α μ n ) k ∥ x 0 − x ( λ ) ∥ 2 + 2 n α σ 2 μ w h e r e σ 2 : = 1 n 2 ∑ i = 1 n ( 1 1 − p ∥ ∇ f i ( x i ( λ ) ) ∥ 2 + λ 2 p ∥ x i ( λ ) − x ˉ ( λ ) ∥ 2 ) \mathbb{E} \left [ \left \| x^k-x(\lambda) \right \|^2 \right ] \le(1-\frac{\alpha \mu}{n})^k\left \| x^0-x(\lambda) \right \|^2+\frac{2n\alpha \sigma^2 }{\mu} \\ \\ where \quad \quad \sigma^2:=\frac{1}{n^2}\sum_{i=1}^{n}(\frac{1}{1-p}\left \| \nabla f_i(x_i(\lambda)) \right \|^2 +\frac{\lambda^2}{p}\left \| x_i(\lambda)-\bar{x}(\lambda) \right \|^2 ) E[ xk−x(λ) 2]≤(1−nαμ)k x0−x(λ) 2+μ2nασ2whereσ2:=n21i=1∑n(1−p1∥∇fi(xi(λ))∥2+pλ2∥xi(λ)−xˉ(λ)∥2)我们需要找到超参 p , α p,α p,α,使得函数能以最快的速率以将误差收敛到最优值的 ( O ( ε ) + 2 n α σ 2 μ ) (\mathcal{O}(\varepsilon )+\frac{2n\alpha\sigma^2}{\mu}) (O(ε)+μ2nασ2) 邻域内,也就是说,实现 ♯ E [ ∥ x k − x ( λ ) ∥ 2 ] ≤ ε ∥ x 0 − x ( λ ) ∥ 2 + 2 n α σ 2 μ \sharp \quad \mathbb{E} \left [ \left \| x^k-x(\lambda) \right \|^2 \right ] \le\varepsilon\left \| x^0-x(\lambda) \right \|^2+\frac{2n\alpha \sigma^2 }{\mu} ♯E[ xk−x(λ) 2]≤ε x0−x(λ) 2+μ2nασ2 推论:当值 p ∗ = λ L + λ p^* =\frac{ λ}{ L+λ} p∗=L+λλ 时,可以令迭代次数和实现 ♯ \sharp ♯ 的预期通信次数两者最小化。
特别地,最佳迭代次数是 2 L + λ μ l o g 1 ε 2\frac{L+\lambda}{ \mu} log\frac{ 1}{\varepsilon} 2μL+λlogε1,并且最佳预期通信次数是 2 λ λ + L L μ l o g 1 ε \frac{2λ}{ λ+L}\frac{ L}{ \mu} log \frac{1}{ ε} λ+L2λμLlogε1。
如果令 p = p ∗ p=p^* p=p∗ 那么 α λ n p = 1 2 \frac{\alpha \lambda}{np}=\frac{1}{2} npαλ=21,并且算法1中的 ♡ \heartsuit ♡ 简化为: x i k = 1 2 ( x i k + x ˉ k ) x_i^k=\frac{1}{2}(x_i^k +\bar{x}^k) xik=21(xik+xˉk)并且局部GD的更新步骤简化为: x i k + 1 = x i k − 1 2 L ∇ f i ( x i k ) x_i^{k+1}=x_i^k-\frac{1}{2L}\nabla f_i(x_i^k) xik+1=xik−2L1∇fi(xik)对于简化后的两个式子,有以下几点发现:
- 虽然本文提出的方法不支持完全平均,因为它太不稳定,但推论表明应该向平均迈出一大步。
- 随着 λ \lambda λ 变小,优化问题 ♣ \clubsuit ♣ 的解将越来越倾向于纯局部模型,即当 λ → 0 λ → 0 λ→0 有 x i ( λ ) → x i ( 0 ) : = a r g min f i x_i(\lambda)→ x_i(0):= arg \min f_i xi(λ)→xi(0):=argminfi。纯局部模型可以在没有任何通信的情况下计算。
L2SGD+
L2GD是SGD的一个特定实例,因此它只线性收敛到一个最优邻域。这意味着,它只能求解具有凸函数性质的优化目标,当函数存在非凸(有局部最优解)区域时,L2GD可能会陷入凹区域。
为了解决上述问题,作者提出将控制变量纳入随机梯度,进一步假设每个局部目标都具有有限和结构,并提出了L2SGD+算法。
假设 f i f_i fi 有个有限和结构: f i ( x i ) = 1 m ∑ j = 1 m f i , j ′ ( x i ) f_i(x_i)=\frac{1}{m}\sum_{j=1}^{m}f_{i,j}'(x_i) fi(xi)=m1j=1∑mfi,j′(xi)令 f i , j ′ f_{i,j}' fi,j′ 强凸且 L − s m o o t h L-smooth L−smooth , 同时 f i f_i fi 是 μ − s t r o n g l y \mu-strongly μ−strongly 凸函数。
篇幅有限,加之本人能力有限,这边就不展开讲解了,有兴趣的同仁可以去看原文的推导证明,还挺有挑战的。
相关文章:

【L2GD】: 无环局部梯度下降
文章链接:Federated Learning of a Mixture of Global and Local Models 发表期刊(会议): ICLR 2021 Conference(机器学习顶会) 往期博客:FLMix: 联邦学习新范式——局部和全局的结合 目录 1.背景介绍2. …...
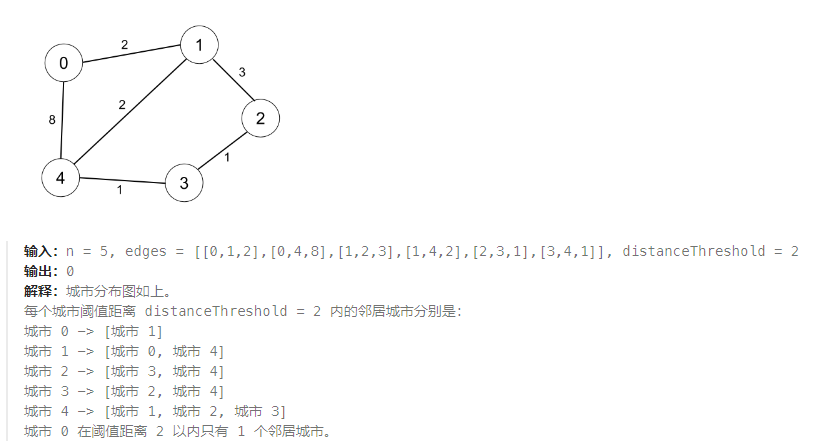
2023-11-14 LeetCode每日一题(阈值距离内邻居最少的城市)
2023-11-14每日一题 一、题目编号 1334. 阈值距离内邻居最少的城市二、题目链接 点击跳转到题目位置 三、题目描述 有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的…...

AdServices归因和iAd归因集成
AdServices framework 是 Apple 专门为 ASA 提供的归因框架 。尤其在ATT 政策推出以后,app 获取用户 IDFA 的比例大幅降低,传统的依靠IDFA 的方法也无法准确归因。 但是 Apple 为 ASA 开了一个后门,其他广告渠道无法获取用户的 IDFA 作为身份…...
关于 内部类 你了解多少?(详解!!)
目录 1. 什么是内部类? 2. 内部类的分类 3. 内部类 3.1 实例内部类 3.2 静态内部类 4. 局部内部类 5. 匿名内部类 6.对象的打印 “不积跬步无以至千里,不积小流无以成江海。”每天坚持学习,哪怕是一点点!!&a…...
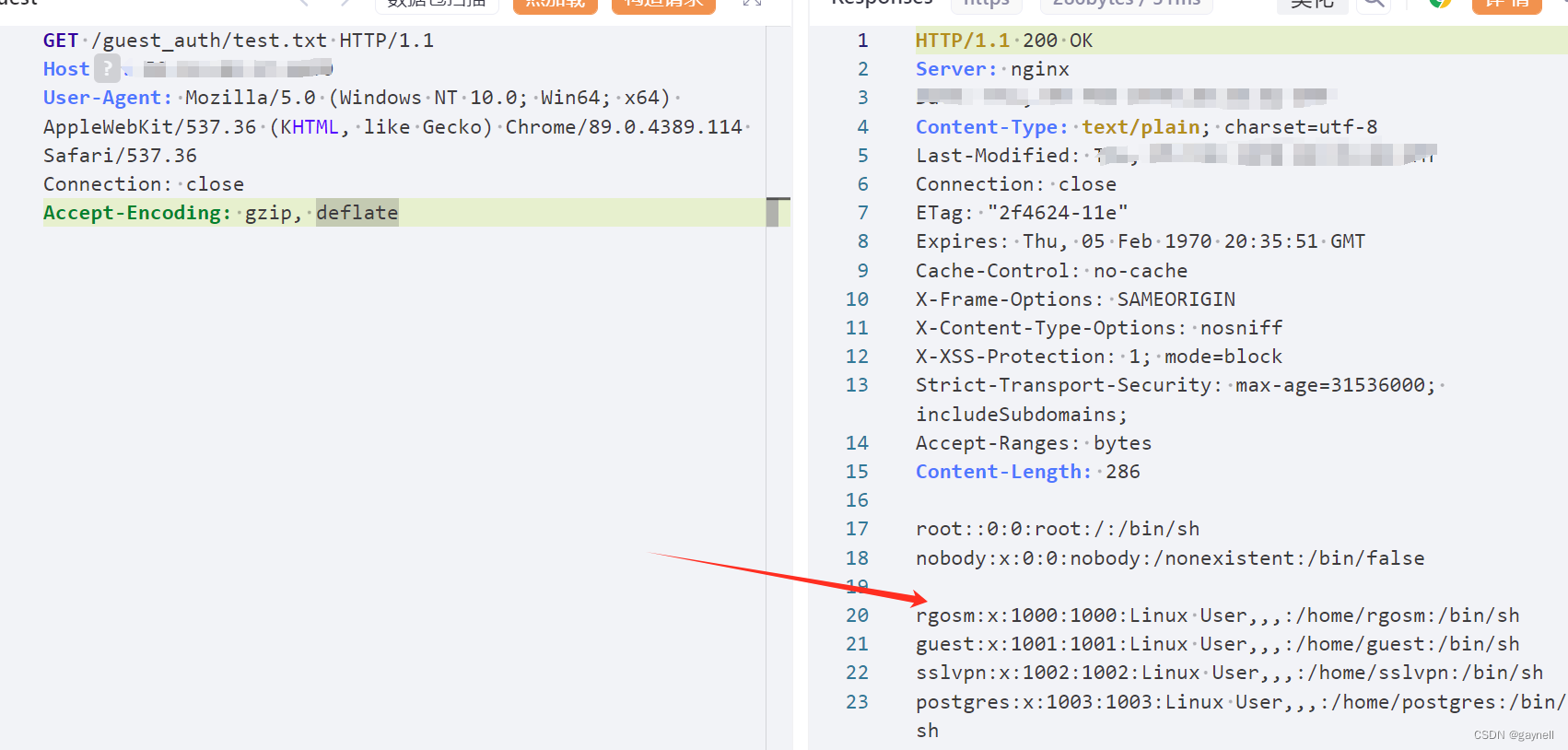
CNVD-2021-09650:锐捷NBR路由器(guestIsUp.php)RCE漏洞复现 [附POC]
文章目录 锐捷NBR路由器guestIsUp.php远程命令执行漏洞(CNVD-2021-09650)复现 [附POC]0x01 前言0x02 漏洞描述0x03 影响版本0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 锐捷NBR路由器guestIsUp.php远程命令执行漏洞(CNVD-2021-09650)复现 [附POC] 0x01 前言 免…...
如何在Docker部署Draw.io绘图工具并远程访问
文章目录 前言1. 使用Docker本地部署Drawio2. 安装cpolar内网穿透工具3. 配置Draw.io公网访问地址4. 公网远程访问Draw.io 前言 提到流程图,大家第一时间可能会想到Visio,不可否认,VIsio确实是功能强大,但是软件为收费࿰…...

Android APK打包的过程主要步骤
Android APK打包的过程可以概括为以下几个主要步骤: 编译源代码:将开发好的Java源代码编译成Dalvik字节码文件(.dex文件),Android安卓该文件包含了Android平台上的运行程序的指令集。打包资源文件:将应用程…...
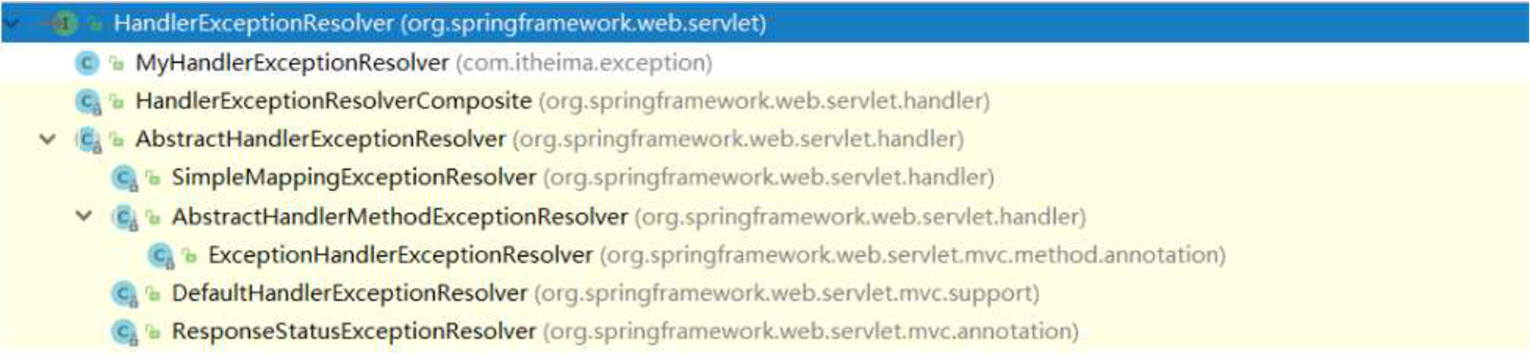
吃透 Spring 系列—MVC部分
目录 ◆ SpringMVC简介 - SpringMVC概述 - SpringMVC快速入门 - Controller中访问容器中的Bean - SpringMVC关键组件浅析 ◆ SpringMVC的请求处理 - 请求映射路径的配置 - 请求数据的接收 - Javaweb常用对象获取 - 请求静态资源 - 注解驱动 标签 ◆ SpringMV…...

Java面试题(每天10题)-------连载(32)
目录 设计模式篇 1、工厂方法模式(利用创建同一接口的不同实例): 2、抽象工厂模式(多个工厂) 3、单例模式(保证对象只有一个实例) 4、原型模式(对一个原型进行复制、克隆产生类…...
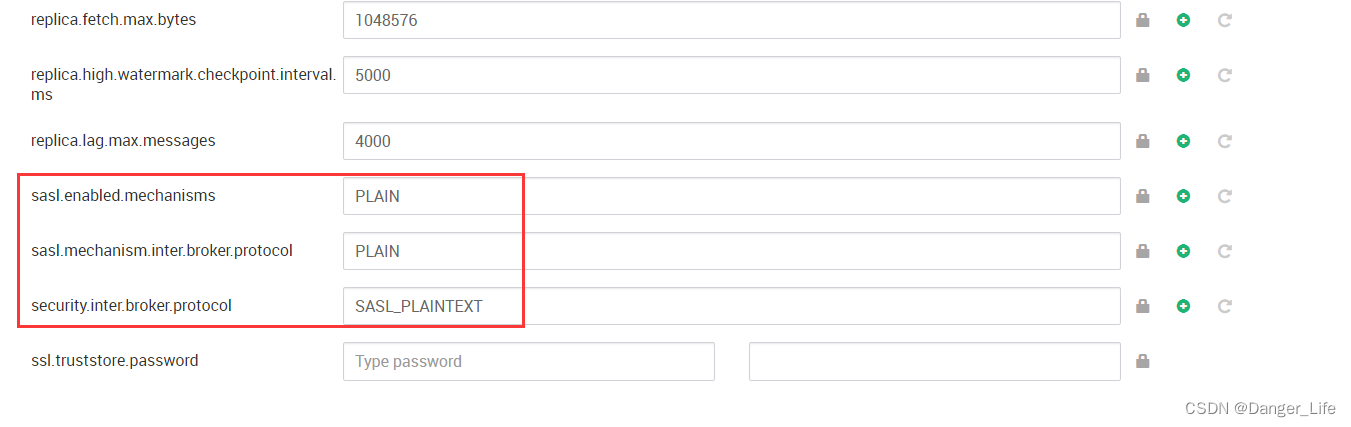
HDP集群Kafka开启SASLPLAINTEXT安全认证
hdp页面修改kafka配置 java代码连接kafka增加对应的认证信息 props.put("security.protocol","SASL_PLAINTEXT");props.put("sasl.mechanism","PLAIN");props.put("sasl.jaas.config","org.apache.kafka.common.securi…...
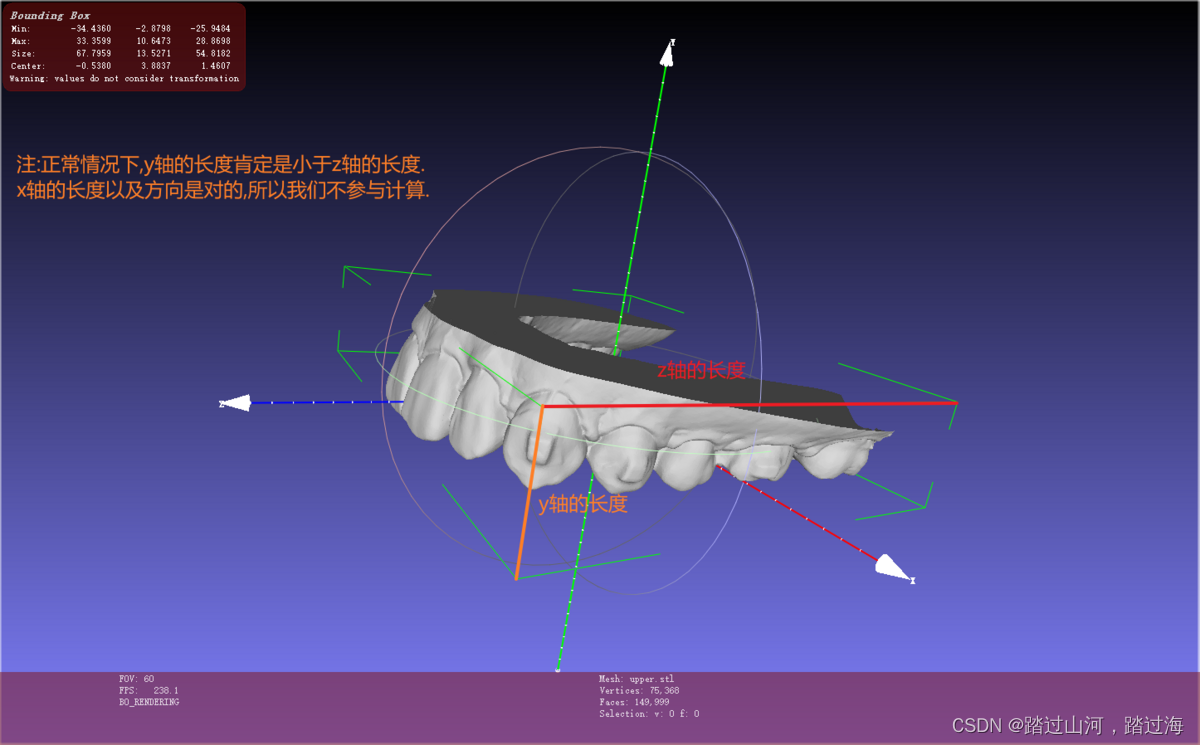
判断上颌下颌的stl模型坐标轴是否正常
文章目录 研究方向:如何判断?又如何纠正?如何判断?Demo实现:先判断一个遍历相关文件夹下的所有病例如何纠正?Demo相关知识点研究方向:如何判断?又如何纠正? 如何判断? 当然,我们不能以坐标的正负来判断 我们看到这个Bounding Box里面有stl模型的xyz三轴方向的最大值与最…...
C/C++---------------LeetCode第1189. “气球” 的最大数量
气球的最大数量 题目及要求统计法在main内使用 题目及要求 给你一个字符串 text,你需要使用 text 中的字母来拼凑尽可能多的单词 “balloon”(气球)。 字符串 text 中的每个字母最多只能被使用一次。请你返回最多可以拼凑出多少个单词 “ba…...
--(三))
Arthas(阿尔萨斯)--(三)
目录 一、Arthas学习 1、class/classloader相关命令一 1、sc 2、sm 2、class/classloader相关命令二 1、jad 2、mc 3、redefine 三、class/classloader相关命令三 一、Arthas学习 Arthas(阿尔萨斯)--(一) Arthas(阿尔萨斯)--(二) 1、class/classloader相关命令一 …...
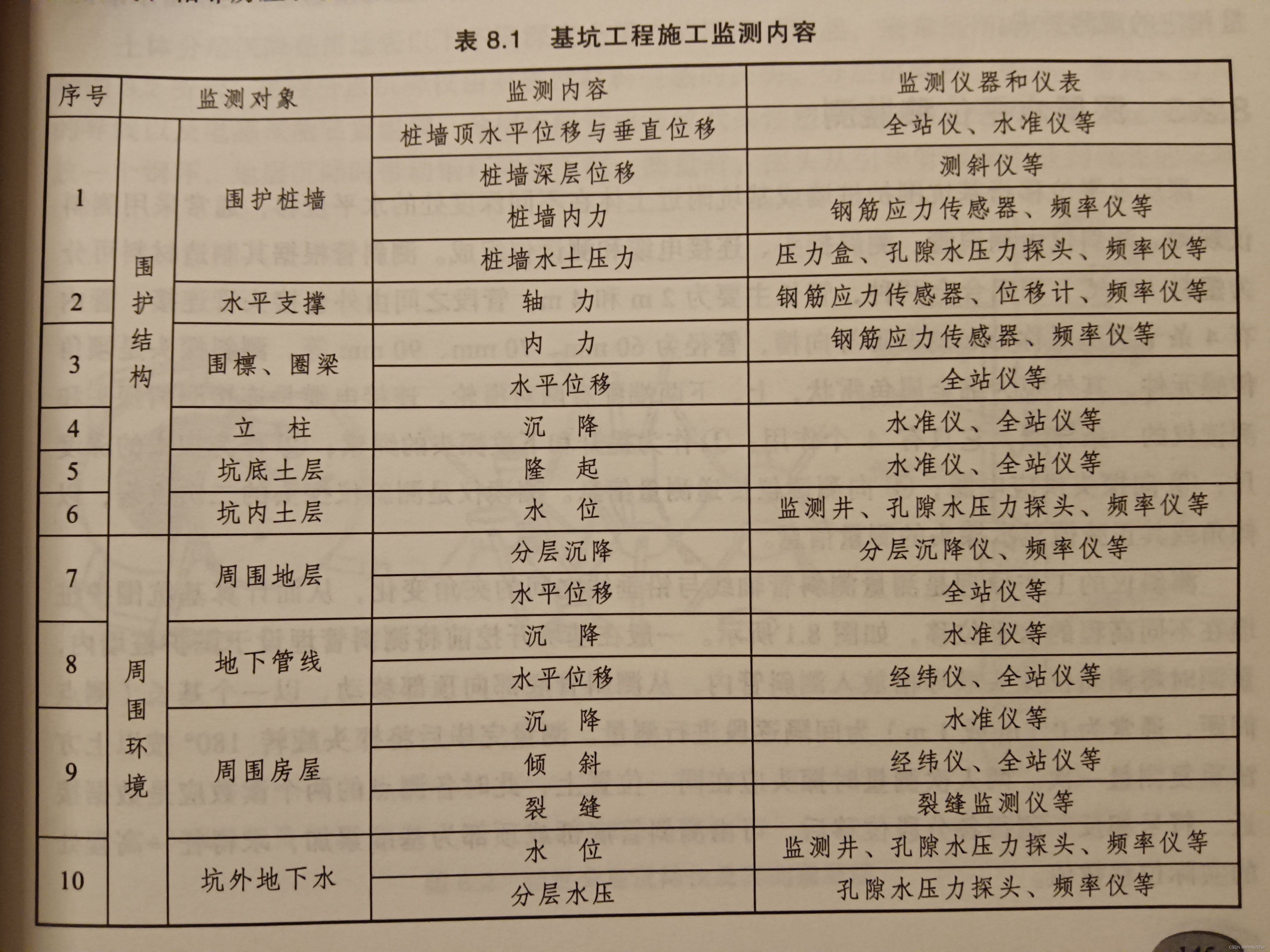
《变形监测与数据处理》笔记/期末复习资料(择期补充更新)
变形: 变形是物体在外来因素作用下产生的形状、大小及位置的变化(随时间域和空间域的变化),它是自然界普遍存在的现象。 变形体: 一般包括工程建筑物、构筑物、大型机械设备以及其他自然和人工对象等。 变形体和变形…...
Linux:进程替换和知识整合
文章目录 进程程序替换替换原理进程替换的理解 环境变量与进程替换命令行解释器实现逻辑 进程程序替换 前面已经学习了子进程的创建,但是子进程的创建不管怎么说,都是父进程代码的一部分,那么实际上如果想要子进程执行新的程序呢?…...

React组件在什么情况下会重新渲染
当我们使用React编写组件时,组件的重新渲染是一个重要的概念。重新渲染是指React组件在特定情况下会重新执行其渲染函数,更新用户界面以反映最新的数据。很多情况下,组件不必要的重新渲染会严重影响性能,所以要充分了解触发组件重…...
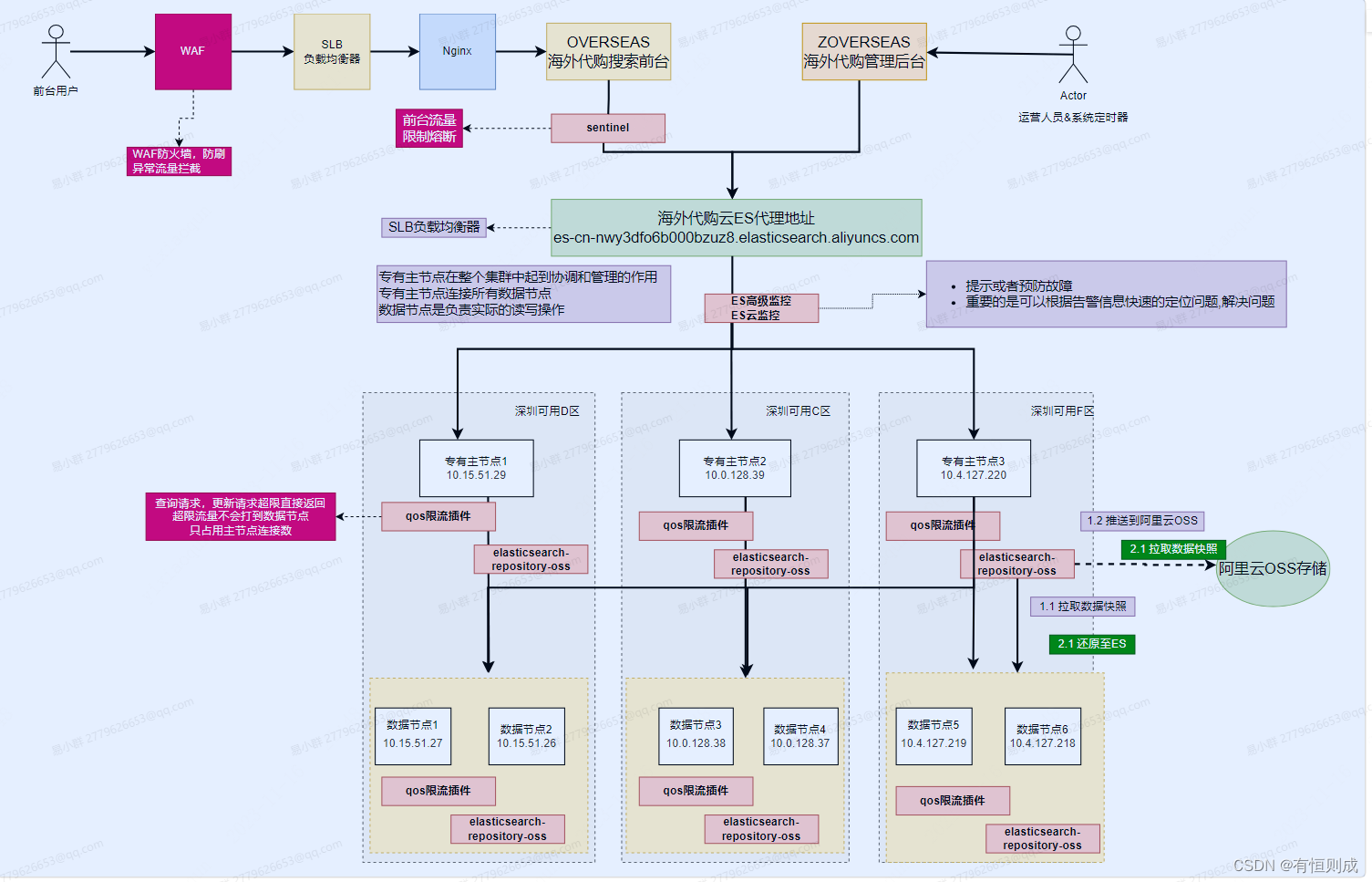
云ES容灾方案
一、ES集群可用性容灾 1.1 云ES集群可用性容灾(使用跨可用区实例) 云ES集群部署在三个可用区,单可用区故障,云ES集群依然可能对外提供服务;两个可用区故障,需要进行控制台切流(集群会自动切的选择主节点) 应用服务部署在二个可用区,单可用区故障,依然可对提供服务1.2 …...

Golang 中的 Context 包
简介 今天,我们将讨论 Go 编程中非常重要的一个主题:context 包。如果你现在觉得它很令人困惑,不用担心 — 在本文结束时,你将像专家一样处理 context! 想象一下,你在一个主题公园,兴奋地准备…...

nginx服务器
nginx反向代理 nginx 反向代理的好处: 提高访问速度 因为nginx本身可以进行缓存,如果访问的同一接口,并且做了数据缓存, nginx就直接可把数据返回,不需要真正地访问服务端,从而提高访问速度。 进行负载均衡…...

电脑常用快捷键
一、Win键(徽标键) 以下是Windows操作系统中使用Win键(徽标键)结合A-Z的所有快捷方式描述: - Win A:打开操作中心,访问系统通知、快速设置和其他功能 - Win B:将焦点设置到任务栏…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
