算法实战:亲自写红黑树之五 删除erase的平衡
本文承接自:
算法实战:亲自写红黑树之一-CSDN博客
算法实战:亲自写红黑树之二 完整代码-CSDN博客
算法实战:亲自写红黑树之三 算法详解-CSDN博客
算法实战:亲自写红黑树之四 插入insert的平衡-CSDN博客
目录
一、入口
二、删除
三、转换中间节点(左右子树都存在)
四、简单情形
五、复杂情形
一、入口
有几个不同参数的删除入口:
bool erase(const_iterator it){T_COMP comp;return erase(it, comp);}//删除并指向下一个iterator& DeleteAndMoveNext(iterator& it){if (end() == it)return it;iterator& ret = it;iterator tmp = ret;++ret;erase(tmp);return ret;}bool erase(const_iterator it, T_COMP& comp){if (it.handle < 0)return true;//DEBUG_LOG<<"要删除节点"<<show(it.handle)<<endi;bool ret = _erase(it.handle);return ret;}bool erase(T_DATA const& data){T_COMP comp;return erase(data, comp);}bool erase(T_DATA const& data, T_COMP& comp){const_iterator it = find(data, comp);if (it.handle < 0)return true;return erase(it, comp);}
最终都进入_erase(h),直接删除一个节点。
在到达这一步之前要先找到要删除的节点,这个属于二叉树的标准算法,很简单。
二、删除
删除的控制代码:
//删除bool _erase(T_SHM_SIZE position){string report;//DEBUG_LOG<<"开始删除...."<<Report(report) <<endi;bool vLeft;//删除的节点是左子节点bool vRed;//删除的节点是红色T_SHM_SIZE p = TREE_NODE::at(position).hParent;//父节点T_SHM_SIZE u;//替换节点bool uRed;//替换节点是红色(-1为黑色)if (TREE_NODE::at(position).hLeft != -1 && TREE_NODE::at(position).hRight != -1){debug_log << "左右都存在,替换为左子树最大值" << endi;if (!__erase_change_middle(position, vLeft, vRed, u, uRed, p))return false;debug();return _erase(position);}else if (-1 == TREE_NODE::at(position).hLeft && -1 == TREE_NODE::at(position).hRight){vLeft = TREE_NODE::at(position).isLeft();vRed = TREE_NODE::at(position).bColorRed;u = -1;uRed = false;if (-1 == p){debug_log << "最后一个节点" << endi;tree_head->hHead = -1;vRed = true;//阻止后面继续处理,删除红色无需额外处理}else{debug_log << "叶子节点" << endi;if (TREE_NODE::at(position).isLeft())TREE_NODE::at(p).hLeft = -1;else TREE_NODE::at(p).hRight = -1;}}else{vLeft = TREE_NODE::at(position).isLeft();vRed = TREE_NODE::at(position).bColorRed;if (-1 != TREE_NODE::at(position).hLeft){debug_log << "左子树存在" << endi;u = TREE_NODE::at(position).hLeft;}else{debug_log << "右子树存在" << endi;u = TREE_NODE::at(position).hRight;}if (-1 == p){debug_log << "根节点" << endi;tree_head->hHead = u;}else{if (vLeft)TREE_NODE::at(p).hLeft = u;else TREE_NODE::at(p).hRight = u;}TREE_NODE::at(u).hParent = p;uRed = TREE_NODE::at(u).bColorRed;p = TREE_NODE::at(u).hParent;}bool ret = true;if (vRed){debug_log << "删除红色节点,不用调整" << endi;}else if (!vRed && uRed){debug_log << "删除黑色节点,替换节点红色改为黑色" << endi;TREE_NODE::at(u).bColorRed = false;}else{debug_log << "删除双黑节点================================================" << endi;ret = _RB_erase_Balance(p, u);}debug();if (ret)__erase_node(position);if (-1 != tree_head->hHead)TREE_NODE::at(tree_head->hHead).bColorRed = false;return ret;}
这个函数的逻辑分为两部分:
- 分析要删除的节点的分支情况,将左右节点都存在的情形改为删除叶子数据节点(不是红黑树意义的叶子节点,指一般意义的叶子节点),然后确定删除节点和替换节点。
- 根据删除节点和替换节点的颜色进行处理,黑节点减少则需要平衡。
三、转换中间节点(左右子树都存在)
很容易把中间节点替换掉,跟左子树最大值或者右子树最小值交换即可。
本代码用__erase_change_middle(h)函数做这件事,将颜色也做了交换(逻辑上相当于不改变结构数据,只交换用户数据,但是我们的用户数据一般都很大,所以反过来操作,改变了除用户数据以外的所有结构数据),执行完毕后红黑树结构仍然正确,删除节点变成了最多只有一个子树的节点。
//删除中间节点,将中间节点替换为左子树最大值(数据不动,改变树结构)bool __erase_change_middle(T_SHM_SIZE const position, bool& vLeft, bool& vRed, T_SHM_SIZE& u, bool& uRed, T_SHM_SIZE& p){string tmp;T_SHM_SIZE new_position = TREE_NODE::at(position).hLeft;if (-1 != new_position){while (-1 != TREE_NODE::at(new_position).hRight){new_position = TREE_NODE::at(new_position).hRight;}}debug_log << "position " << position << " new_position " << new_position << endi;debug_log << "position " << position << TREE_NODE::at(position).toString(tmp) << endi;debug_log << "new_position " << new_position << TREE_NODE::at(new_position).toString(tmp) << endi;vLeft = false;vRed = TREE_NODE::at(new_position).bColorRed;p = TREE_NODE::at(new_position).hParent;debug_log << "p " << TREE_NODE::at(p).toString(tmp) << endi;if (p != position){debug_log << "非直接对调 p " << TREE_NODE::at(p).toString(tmp) << ende;TREE_NODE t;t._CopyWithoutData(TREE_NODE::at(new_position));TREE_NODE::at(new_position)._CopyWithoutData(TREE_NODE::at(position));TREE_NODE::at(position)._CopyWithoutData(t);debug_log << "position " << TREE_NODE::at(position).toString(tmp) << endi;debug_log << "new_position " << TREE_NODE::at(new_position).toString(tmp) << endi;//注意,这里无法用isLeft来判断,因为父节点的hLeft和hRight是旧数据if (TREE_NODE::at(new_position).hParent != -1){if (TREE_NODE::at(TREE_NODE::at(new_position).hParent).hLeft == position)TREE_NODE::at(TREE_NODE::at(new_position).hParent).hLeft = new_position;else TREE_NODE::at(TREE_NODE::at(new_position).hParent).hRight = new_position;}if (TREE_NODE::at(position).hParent != -1){if (TREE_NODE::at(TREE_NODE::at(position).hParent).hLeft==new_position)TREE_NODE::at(TREE_NODE::at(position).hParent).hLeft = position;else TREE_NODE::at(TREE_NODE::at(position).hParent).hRight = position;}if (TREE_NODE::at(new_position).hLeft != -1)TREE_NODE::at(TREE_NODE::at(new_position).hLeft).hParent = new_position;if (TREE_NODE::at(position).hLeft != -1)TREE_NODE::at(TREE_NODE::at(position).hLeft).hParent = position;if (TREE_NODE::at(new_position).hRight != -1)TREE_NODE::at(TREE_NODE::at(new_position).hRight).hParent = new_position;if (TREE_NODE::at(position).hRight != -1)TREE_NODE::at(TREE_NODE::at(position).hRight).hParent = position;}else{debug_log << "直接对调 p " << TREE_NODE::at(p).toString(tmp) << endi;TREE_NODE t;t._CopyWithoutData(TREE_NODE::at(new_position));TREE_NODE::at(new_position)._CopyWithoutData(TREE_NODE::at(position));TREE_NODE::at(position)._CopyWithoutData(t);debug_log << "position " << TREE_NODE::at(position).toString(tmp) << endi;debug_log << "new_position " << TREE_NODE::at(new_position).toString(tmp) << endi;//注意,这里无法用isLeft来判断,因为父节点的hLeft和hRight是旧数据if (TREE_NODE::at(new_position).hParent != -1){if (TREE_NODE::at(TREE_NODE::at(new_position).hParent).hLeft == position)TREE_NODE::at(TREE_NODE::at(new_position).hParent).hLeft = new_position;else TREE_NODE::at(TREE_NODE::at(new_position).hParent).hRight = new_position;}TREE_NODE::at(position).hParent = new_position;TREE_NODE::at(new_position).hLeft=position;if (TREE_NODE::at(position).hLeft != -1)TREE_NODE::at(TREE_NODE::at(position).hLeft).hParent = position;if (TREE_NODE::at(new_position).hRight != -1)TREE_NODE::at(TREE_NODE::at(new_position).hRight).hParent = new_position;if (TREE_NODE::at(position).hRight != -1)TREE_NODE::at(TREE_NODE::at(position).hRight).hParent = position;}//如果是根节点if (-1 == TREE_NODE::at(new_position).hParent){TREE_NODE::at(new_position).bColorRed = false;tree_head->hHead = new_position;}debug_log << "position " << TREE_NODE::at(position).toString(tmp) << endi;debug_log << "new_position " << TREE_NODE::at(new_position).toString(tmp) << endi;debug();return true;}
这个代码不复杂,就是累。
四、简单情形
现在要删除的节点要么没有子树,要么只有一个子树(说起来是子树,其实最多就是一个红节点,否则必定违反红黑树规则),只需要把子树接上去就可以了,然后把要删除的节点扔掉。
这里我们还是用一般二叉树的概念来理解,以下说的节点都是数据节点,不包括空节点。
- 如果删除节点是红节点,不管下面有没有子树,不用平衡,因为不影响规则。
- 如果删除节点是黑节点而下面有一个红节点(前面已经说了,没有更多可能性),把这个红节点变成黑节点就行了。
- 如果删除节点是黑节点而下面没有可供变色的红节点(也就是没有子节点,红黑树规则不允许下面有黑色数据节点,因为只有一个子树,另外一边深度是0),这就导致红黑树规则被破坏,很多文章称这种情况为“双黑”,其实就是黑节点少了。
第三种情形就被称为“复杂情形”,需要调用_RB_erase_Balance()来平衡。
五、复杂情形
前面已经说了,所谓复杂情形就是少了一个黑节点,现在涉及到这么几个节点:
u 替换节点,也就是出问题的节点,这个节点的高度比兄弟少一。这个节点可能是是空节点。
p 替换节点的父节点
s 替换节点的兄弟节点
由于红黑树的规则限制,最初进入这种情形只可能是被删除节点下没有子节点,所以一定是p的一边为空另一边黑高为1。递归之后黑高少一的节点就有了各种可能,可能是红色或黑色,可能有或没有子节点。
重新平衡有三种策略:
- 如果能把p改成黑同时让s黑高减一,这样就恢复平衡了,这要求p为红,p为红则s必为黑,如果s的子节点均为黑(此时s的子节点必定都是空节点,否则违反红黑树规则),只需要将p和s颜色交换就可以了。
- 另一边如果有红色节点,能挪过来改成黑色,平衡就完成了。按照红色节点的位置不同,需要有不同的挪法,虽然繁琐但并不困难。
- 另一边如果有红色节点,挪过来也不能平衡,想办法把问题往上移,递归处理。
| p | s | ss | 处理 | |
| 1 | 黑 | 黑 | 黑黑/不存在 | p、s交换颜色,问题上移,递归 |
| 2 | 黑 | 黑 | 红红 | 挪一个红改成黑 |
| 3 | 黑 | 红 | 黑黑-[红红红红] | 旋转p,p、s交换颜色,p还是少1,但是变色了,重新处理p,递归 |
| 4 | 红 | 黑 | 红红 | 挪一个红改成黑 |
| 5 | 红 | 黑 | 黑黑/不存在 | p、s交换颜色 |
上表是所有情形,“不存在”指的是空节点,也是黑色。ss指的是s的子节点。“红红”也可能是只有一个红,因为处理时只要有一个红就不用管另一个。第三种情形的ss是双黑,后面还可能有红色子节点,不过与算法无关。
为什么只有五种组合而不是八种?因为不允许连续红,另外三种不可能存在。
上面第二种和第四种处理方式相同,因为并不关心p的颜色,通过挪一个改成黑,下面就平衡了。
代码的实际处理逻辑是从ss开始判断的,先分成ss至少有一个红和没有红,然后没有红的分三种,有红的分四种(所谓四种不过是四种结构的挪法而已)。
代码如下:
//删除时做平衡,u可能是空节点bool _RB_erase_Balance(T_SHM_SIZE p, T_SHM_SIZE u){if (-1 == p){debug_log << "已经到顶,结束" << endi;return true;}string tmp;debug_log << "p " << TREE_NODE::at(p).toString(tmp) << endi;if (u != -1)debug_log << "u " << TREE_NODE::at(u).toString(tmp) << endi;else debug_log << "u -1" << endi;bool isL = (u == TREE_NODE::at(p).hRight);//兄弟节点是否是左节点T_SHM_SIZE s = (isL ? TREE_NODE::at(p).hLeft : TREE_NODE::at(p).hRight);T_SHM_SIZE r = -1;//s的红色子节点bool is_rL;//s的红色子节点是否是左节点debug_log << "平衡:p " << p << " u " << u << " s " << s << " TREE_NODE::at(s).hRight " << TREE_NODE::at(s).hRight << endi;if (TREE_NODE::at(s).hRight != -1 && TREE_NODE::at(TREE_NODE::at(s).hRight).bColorRed){r = TREE_NODE::at(s).hRight;is_rL = false;}else if (TREE_NODE::at(s).hLeft != -1 && TREE_NODE::at(TREE_NODE::at(s).hLeft).bColorRed){r = TREE_NODE::at(s).hLeft;is_rL = true;}else{r = -1;is_rL = false;//无意义}debug_log << "p " << p << " u " << u << " s " << s << " r(-1表示双黑) " << r << endi;debug();if (-1 == r){debug_log << "s子节点均为黑" << endi;if (TREE_NODE::at(p).bColorRed){debug_log << "p为红,s必为黑 s改为红p改为黑 结束" << endi;//s子节点均为黑,p改为黑,所以s改为红是安全的,不会造成双红TREE_NODE::at(s).bColorRed = true;TREE_NODE::at(p).bColorRed = false;debug();}else{debug_log << "p为黑" << endi;if (!TREE_NODE::at(s).bColorRed){debug_log << "s为黑 s改为红平衡下层并向上递归" << endi;//p的左右分支均少1,所以p成为新的双黑节点//置s为红,p为新的u,递归TREE_NODE::at(s).bColorRed = true;debug();return _RB_erase_Balance(TREE_NODE::at(p).hParent, p);}else{debug_log << "s为红 " << TREE_NODE::at(s).toString(tmp) << endi;debug_log << TREE_NODE::at(TREE_NODE::at(s).hParent).toString(tmp) << endi;if (TREE_NODE::at(s).isLeft()){debug_log << "s为左 " << s << endi;//右旋p_RRotate(p);}else{debug_log << "s为右" << endi;_LRotate(p);}//p和s变色TREE_NODE::at(s).bColorRed = false;TREE_NODE::at(p).bColorRed = true;debug();//此时深度情况不变,但p变成了红,重新对p和u做平衡处理return _RB_erase_Balance(p, u);}}}else{if (isL && is_rL){debug_log << "LL" << ende;TREE_NODE::at(r).bColorRed = TREE_NODE::at(s).bColorRed;TREE_NODE::at(s).bColorRed = TREE_NODE::at(p).bColorRed;_RRotate(p);TREE_NODE::at(p).bColorRed = false;}else if (isL && !is_rL){debug_log << "LR" << endi;debug();TREE_NODE::at(r).bColorRed = TREE_NODE::at(p).bColorRed;debug();_LRotate(s);debug();_RRotate(p);debug();TREE_NODE::at(p).bColorRed = false;debug();}else if (!isL && is_rL){debug_log << "RL------------------------" << endi;debug();TREE_NODE::at(r).bColorRed = TREE_NODE::at(p).bColorRed;debug();_RRotate(s);debug();string tmp;debug_log << "p " << TREE_NODE::at(p).toString(tmp) << endi;debug_log << "s " << TREE_NODE::at(p).toString(tmp) << endi;_LRotate(p);debug();TREE_NODE::at(p).bColorRed = false;debug();}else if (!isL && !is_rL){debug_log << "RR" << endi;TREE_NODE::at(r).bColorRed = TREE_NODE::at(s).bColorRed;TREE_NODE::at(s).bColorRed = TREE_NODE::at(p).bColorRed;_LRotate(p);TREE_NODE::at(p).bColorRed = false;}else{thelog << "非预期的状态" << ende;return false;}}return true;}
我感觉吧,我应该刚好解决了一部分人的困惑。
(这里是结束,而且是整个系列的结束)
相关文章:

算法实战:亲自写红黑树之五 删除erase的平衡
本文承接自: 算法实战:亲自写红黑树之一-CSDN博客 算法实战:亲自写红黑树之二 完整代码-CSDN博客 算法实战:亲自写红黑树之三 算法详解-CSDN博客 算法实战:亲自写红黑树之四 插入insert的平衡-CSDN博客 目录 一、入口…...
春秋云境靶场CVE-2021-41402漏洞复现(任意代码执行漏洞)
文章目录 前言一、CVE-2021-41402描述二、CVE-2021-41402漏洞复现1、信息收集1、方法一弱口令bp爆破2、方法二7kb扫路径,后弱口令爆破 2、找可能可以进行任意php代码执行的地方3、漏洞利用找flag 总结 前言 此文章只用于学习和反思巩固渗透测试知识,禁止…...

12 Go的接口
概述 在上一节的内容中,我们介绍了Go的作用域,包括:局部作用域、全局作用域、命名空间作用域等。在本节中,我们将介绍Go的接口。Go语言中的接口是一种类型,它定义了一组函数的集合。接口是一种抽象的描述,它…...

Python编程-----并行处理应用程序
目录 一.进程 二.线程 三.Python标准库中并行处理的相关模块 Threading模块 (1)使用Thread对象创建线程 (2)自定义派生于Thread的对象 (3)线程加入join() (4)用户线程和daemon线程 (5)Timer线程 线…...
kubernetes集群编排——istio
官网:https://istio.io/latest/zh/about/service-mesh/ 部署 [rootk8s2 ~]# tar zxf istio-1.19.3-linux-amd64.tar.gz [rootk8s2 ~]# cd istio-1.19.3/[rootk8s2 istio-1.19.3]# export PATH$PWD/bin:$PATH demo专为测试准备的功能集合 [rootk8s2 istio-1.19.3]# i…...
mfc140u.dll丢失的解决方法,以及mfc140u.dll解决方法的优缺点
在使用电脑过程中,有时会遇到一些与动态链接库文件(DLL)相关的错误。其中,mfc140u.dll丢失的错误是较为常见的一种。当这个关键的mfc140u.dll文件丢失或损坏时,可能会导致某些应用程序无法正常运行。在本文中ÿ…...

2源码安装网络协议
2.2源码安装/网络协议 一、源码包应用场景 有时我们所用的内核版本太旧,系统自带的库(如libstdc.so.6)版本低或者依赖的其他软件版 本较低,导致无法安装目标软件。 软件/库其实是对机器汇编指令集的封装,在X86体系下…...
未来服务器操作系统的趋势与展望
摘要: 随着云计算、大数据和人工智能不断的发展,服务器操作系统也需要随之进行新一轮的升级。本文通过分析当前服务器操作系统的现状,探讨了未来服务器操作系统的趋势和展望,并针对一些关键问题提出了解决方案。 一、引言 服务器…...
VB.net WebBrowser网页元素抓取分析方法
在用WebBrowser编程实现网页操作自动化时,常要分析网页Html,例如网页在加载数据时,常会显示“系统处理中,请稍候..”,我们需要在数据加载完成后才能继续下一步操作,如何抓取这个信息的网页html元素变化&…...
整体方案)
自建ES6.2.4切阿里云商业版ES(7.10)整体方案
一、切换目的&阿里云商业版ES版本选择 1.1 升级切换阿里云商业版7.10目的 自建的Elasticsearch服务运维难度高,操作复杂,需要手动调整资源,遇到性能瓶颈时优化难度相对云上Elasticsearch较大。使用阿里云提供的ES服务,提高系统稳定性使用云服务es,易于备份,数据恢复…...

Vue实现封装自定义指令
目录 一、什么是自定义指令? 二、自定义指令的使用 Vue中的自定义指令使用Vue.directive函数进行定义。该函数接受两个参数,第一个是指令名称,第二个是指令选项对象。 上述代码中,我们定义了一个名为my-directive的自定义指令…...
<MySQL> 查询数据进阶操作 -- 聚合查询
目录 一、聚合查询概述 二、聚合函数查询 2.1 常用函数 2.2 使用函数演示 2.3 聚合函数参数为*或列名的查询区别 2.4 字符串不能参与数学运算 2.5 具有误导性的结果集 三、分组查询 group by 四、分组后条件表达式查询 五、MySQL 中各个关键字的执行顺序 一、聚合查询…...

arm开发板
一个简单的hello world程序 minicom用来和开发板之间交互并且可以向开发板传输文件。打印hello world字符串。在linux虚拟机上编译我的代码,使用的交叉编译工具是arm-linux-gnueabihf-gcc (hard float) 可以使用 readelf -h libc.so.6 查看开发板是不是(…...
nodejs+vue教室管理系统的设计与实现-微信小程序-安卓-python-PHP-计算机毕业设计
用户 用户管理:查看,修改自己的个人信息 教室预约:可以预约今天明天的教室,按着时间段预约(可多选),如果当前时间超过预约时间段不能预约该时间段的教室 预约教室的时候要有个预约用途ÿ…...
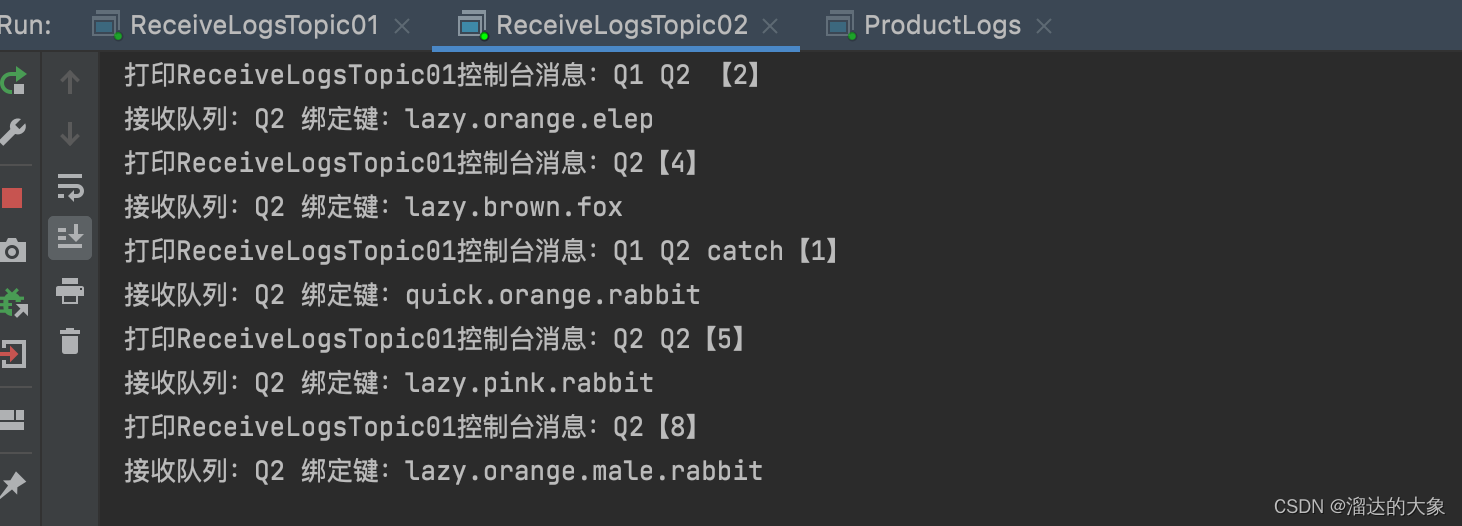
rabbitMQ的Topic模式的生产者与消费者使用案例
topic模式 RoutingKey 按照英文单词点号多拼接规则填充。其中消费者匹配规则时候 * 代表一个单词,#表示多个单词 消费者C1的RoutingKey 规则按照*.orange.* 匹配 绑定队列Q1 package com.esint.rabbitmq.work05;import com.esint.rabbitmq.RabbitMQUtils; import …...

【软考篇】中级软件设计师 第五部分
中级软件设计师 第五部分 三十六. 下午题变动题型参考答案例题一 如何保持数据流图平衡例题二 结构化语言例题三 关系模式例题四 用例关系内涵例题五 观察者模式 三十七:下午题第四题往年算法部分参考答案 读前须知: 【软考篇】中级软件设计师 学前须知 …...

论文阅读——RetNet
transformer的问题:计算量大,占用内存大,不好部署。 所以大家在找能解决办法,既能和transformer表现一样好,又能在推理阶段计算复杂度很低。 这些方法大概分类三类:一是代替transformer非线性注意力机制的…...
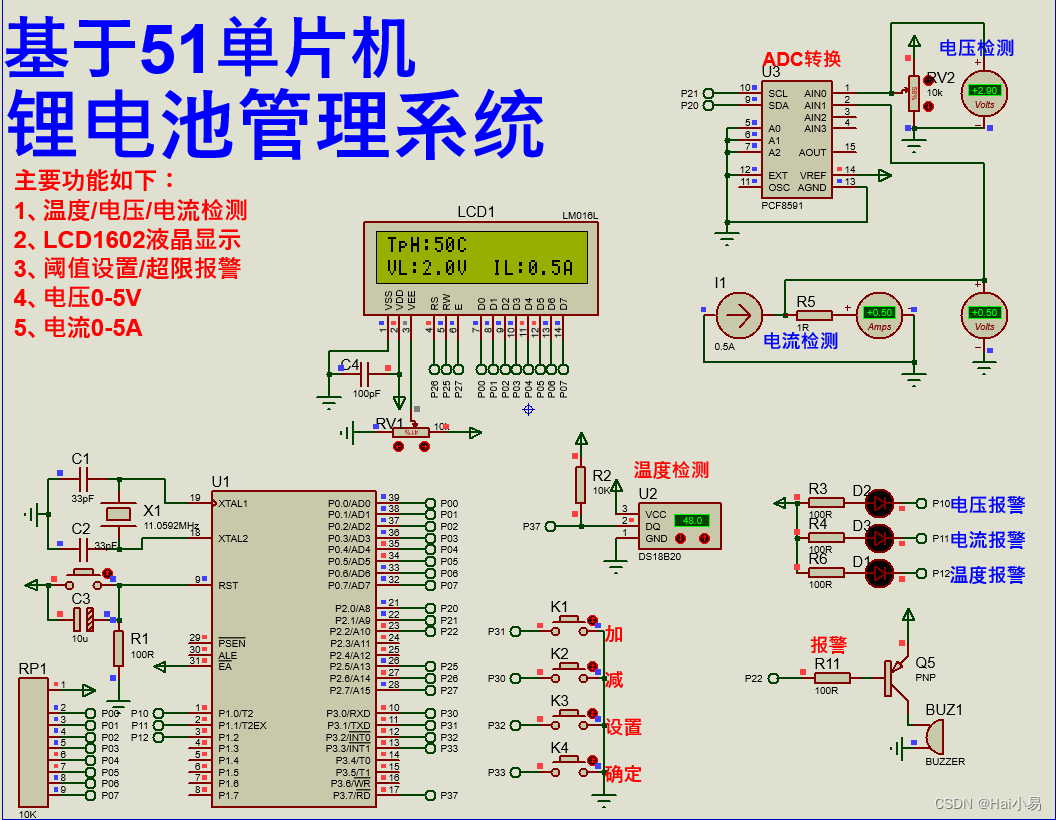
【Proteus仿真】【51单片机】锂电池管理系统
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用LCD1602显示模块、DS18B20温度传感器、PCF8691 ADC模块、按键、LED蜂鸣器模块等。 主要功能: 系统运行后,LCD1602显示温度…...

【工具使用-VScode】设置 VSCode 的自动保存功能
要设置 VSCode 的自动保存功能,请按照以下步骤进行操作: 打开 VSCode 编辑器。在顶部菜单中选择 “文件(File)”。选择 “首选项(Preferences)”。在下拉菜单中选择 “设置(Settings࿰…...

常用Git命令记录
持续补充… git add:提交到暂存区git remote add <remote_name> <remote_url> : 添加一个新的远程仓库。指定一个远程仓库的名称和 URL,将其添加到当前仓库中。git commit:暂存区提交到本地仓库;-m:添加日…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
