电子技术——AB类输出阶
电子技术——AB类输出阶

原理
交越失真可以通过通过一个较小的偏置电流解除,如下图:
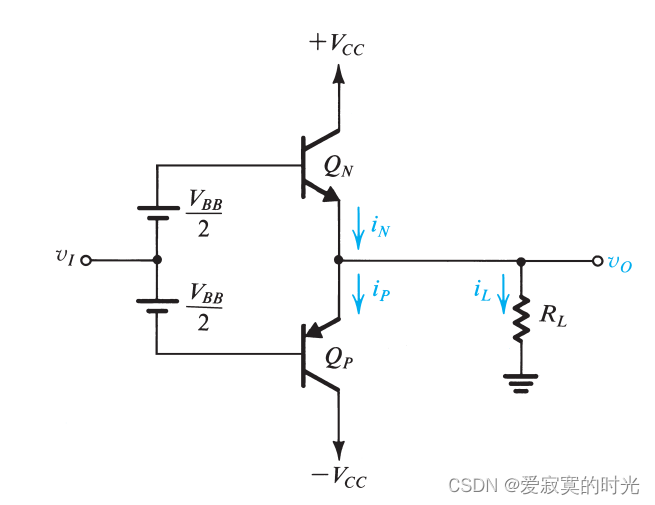
QNQ_NQN 和 QPQ_PQP 的基极之间存在偏置电压 VBBV_{BB}VBB 。对于完美匹配的晶体管,当 vI=0v_I = 0vI=0 的时候,此时 vO=0v_O = 0vO=0 。每一个晶体管都存在偏置电流:
iN=iP=IQ=ISeVBB/2VTi_N = i_P = I_Q = I_S e^{V_{BB}/2V_T} iN=iP=IQ=ISeVBB/2VT
静态偏置电流由电压 VBBV_{BB}VBB 产生。
当 vIv_IvI 正向增大的时候,此时输出电压为:
vO=vI+VBB2−vBENv_O = v_I + \frac{V_{BB}}{2} - v_{BEN} vO=vI+2VBB−vBEN
若设置偏置电压 VBB2=vBEN\frac{V_{BB}}{2} = v_{BEN}2VBB=vBEN ,那么发射极将完美跟随基极电压。
此时会有 iLi_LiL 的电流通过负载,有:
iN=iP+iLi_N = i_P + i_L iN=iP+iL
由于 iNi_NiN 的增大会引起 vBENv_{BEN}vBEN 的增大,这会导致跟随偏移。然而我们知道环路电压不变,即:
vBEN+vEBP=VBBv_{BEN} + v_{EBP} = V_{BB} vBEN+vEBP=VBB
说明 vBENv_{BEN}vBEN 增大会引起 vEBPv_{EBP}vEBP 减小,最终导致 iPi_PiP 减小。更具体的:
VTlniNIS+VTlniPIS=2VTlnIQISV_T\ln{\frac{i_N}{I_S}} + V_T\ln{\frac{i_P}{I_S}} = 2V_T\ln{\frac{I_Q}{I_S}} VTlnISiN+VTlnISiP=2VTlnISIQ
这导出:
iNiP=IQ2i_Ni_P = I_Q^2 iNiP=IQ2
联立导出 iNi_NiN 和 iLi_LiL 的关系:
iN2−iLiN−IQ2=0i_N^2 - i_Li_N - I_Q^2 = 0 iN2−iLiN−IQ2=0
根据上述的推导,我们发现在信号正半周期的时候,此时负载电流由 QNQ_NQN 提供,作为射极电压跟随器。同时 QPQ_PQP 的导通电流将随着 vOv_OvO 的增大而减小,对于较大的 vOv_OvO 此时 QPQ_PQP 的导通电流可以忽略不计。
同理对于负半周期,此时负载电流由 QPQ_PQP 提供,作为射极电压跟随器。同时 QNQ_NQN 的导通电流将随着 vOv_OvO 的增大而减小,对于较大的 vOv_OvO 此时 QNQ_NQN 的导通电流可以忽略不计。
我们得出结论,AB类输出阶的行为和B类输出阶的行为大致相似。其中有一点不同,对于较小的 vIv_IvI 两个晶体管均导通,当 vIv_IvI 增大或者减小两个晶体管都工作在导通区域,因为两个晶体管是平滑过渡,因此不存在交越失真。下图展示了AB类输出阶的传导曲线:

AB类输出阶的功率推导和B类大致相似。唯一的区别是在静态点的时候,此时每一个晶体管都存在静态耗散功率 VCCIQV_{CC}I_QVCCIQ 。因为 IQI_QIQ 非常小,远小于最大负载电流,因此静态耗散功率基本上很小。特别的,我们可以将静态耗散功率加到最大耗散功率上,来计算最大安全功率。
输出阻抗
若我们假设信号源 vIv_IvI 是理想的,则AB类输出阶的输出阻抗可以由下图决定:
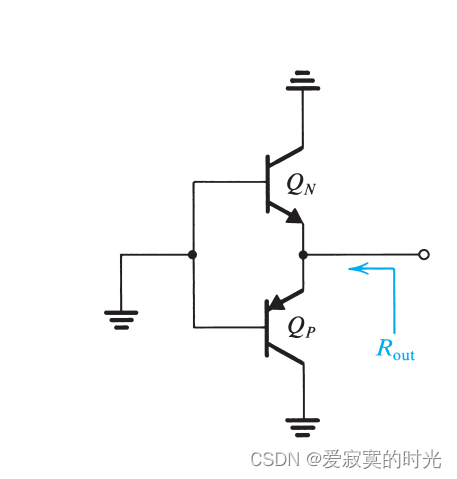
输出阻抗为:
Rout=reN∣∣rePR_{out} = r_{eN} || r_{eP} Rout=reN∣∣reP
这里 reNr_{eN}reN 和 rePr_{eP}reP 是小信号模型下 QNQ_NQN 和 QPQ_PQP 的射极电阻。对于给定的电流,有:
reN=VTiNr_{eN} = \frac{V_T}{i_N} reN=iNVT
reP=VTiPr_{eP} = \frac{V_T}{i_P} reP=iPVT
也就是:
Rout=VTiN∣∣VTiP=VTiN+iPR_{out} = \frac{V_T}{i_N} || \frac{V_T}{i_P} = \frac{V_T}{i_N + i_P} Rout=iNVT∣∣iPVT=iN+iPVT
因为当 iNi_NiN 增大的时候 iPi_PiP 减小,反之亦然,输出阻抗可以近似的看成是一个固定的值和 vI=0v_I = 0vI=0 的静态点相同。在较大的输出电流的情况下,此时 iNi_NiN 或者是 iPi_PiP 占主导,此时 RoutR_{out}Rout 降低。
相关文章:

电子技术——AB类输出阶
电子技术——AB类输出阶 原理 交越失真可以通过通过一个较小的偏置电流解除,如下图: QNQ_NQN 和 QPQ_PQP 的基极之间存在偏置电压 VBBV_{BB}VBB 。对于完美匹配的晶体管,当 vI0v_I 0vI0 的时候,此时 vO0v_O 0vO0 。每…...

Archlinux个人安装流程
操作环境: 时间:2023-02-17 电脑型号:联想拯救者R720 cpu:Intel Core i5-7300HQ 4x 3.5GHz gpu:NVIDIA GeForce GTX 1050 Ti 安装系统: 1.下载镜像: 请访问https://archlinux.org/查找镜…...
【Autoware】2小时安装Autoware1.13(保姆级教程)
前言:ROS的出现使得机器人软件开发更加快速和模块化,在此基础上,Autoware.ai开源项目可以让我们很容易地将一套完整的自动驾驶软件部署到我们的测试车辆上,并见证它跑起来! 文章目录1.Autoware简介2.电脑软硬件配置要求…...
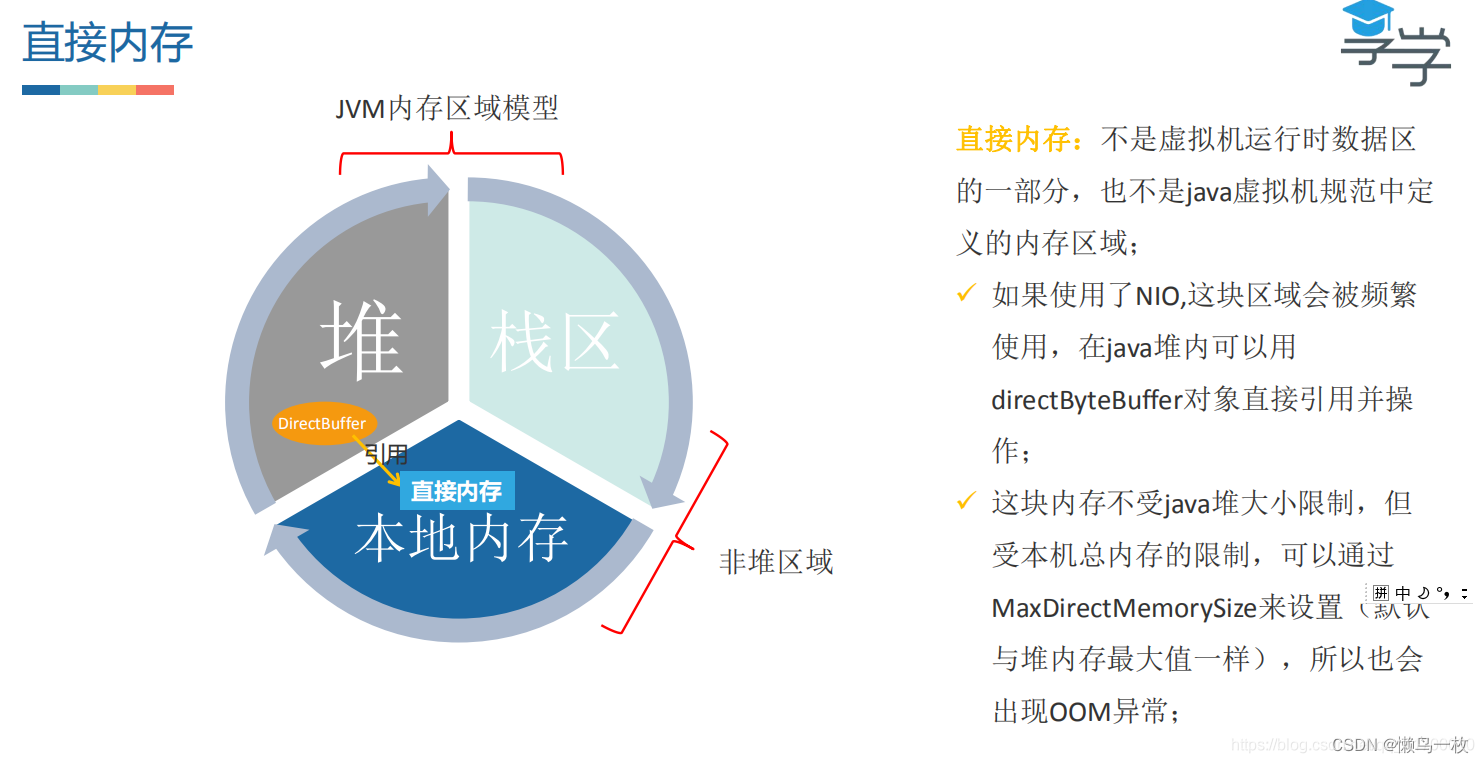
JVM 堆内存模型
方法区和永久代的关系 方法区与 Java 堆一样,是各个线程共享的内存区域,它用于存储已被虚拟机加载的类信息、常量、静态变量、即时编译器编译后的代码等数据。虽然 Java 虚拟机规范把方法区描述为堆的一个逻辑部分,但是它却有一个别名叫做 N…...
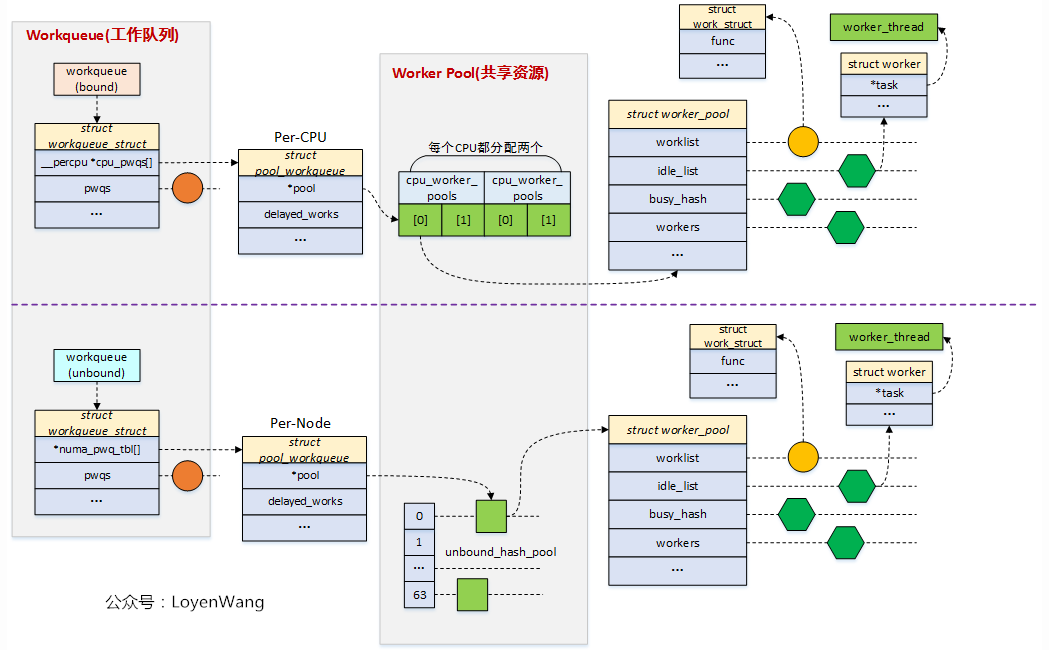
linux-中断下半部
引用preempt宋宝华: 是谁关闭了Linux抢占,而抢占又关闭了谁?Linux用户抢占和内核抢占详解(概念, 实现和触发时机)--Linux进程的管理与调度(二十)内核抢占实现(preempt)Linux中的preempt_count - 知乎 (zhihu.com)linux 中断子系统…...
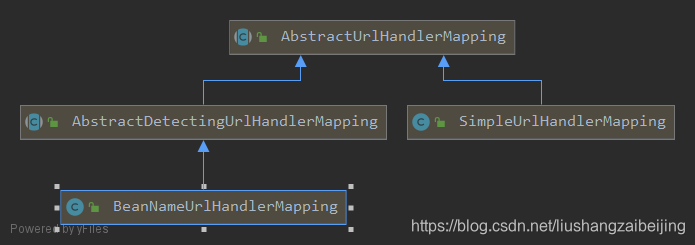
SpringMVC源码:HandlerMapping加载1
参考资料: 《SpringMVC源码解析系列》 《SpringMVC源码分析》 《Spring MVC源码》 写在开头:本文为个人学习笔记,内容比较随意,夹杂个人理解,如有错误,欢迎指正。 前文: 《SpringMVC源码&a…...

【ArcGIS】12 投影
问题描述 在处理地理数据时,可能会遇到以下关于投影的问题: DEM缺少投影,提取流域会报错图层只有地理坐标系,没有投影坐标系,无法测量距离、计算面积等要素图层投影偏移量错误,与实际位置有偏差总之,投影对各种地理操作影响很大,有必要深入理解。 投影说明 在ArcGIS…...

【微信小程序-原生开发+TDesign】通用功能页封装——地点搜索(含腾讯地图开发key 的申请方法)
效果预览 核心技能点 调用腾讯地图官方的关键字地点搜索功能,详见官方文档 https://lbs.qq.com/miniProgram/jsSdk/jsSdkGuide/methodGetsuggestion 完整代码实现 地点输入框 <t-input value"{{placeInfo.title}}" bindtap"searchPlace" dis…...

h5: 打开手机上的某个app
1、android端:直接通过URL Scheme方式打开。2、ios端(2种):(1)使用URL Scheme方式打开。(2)使用Universal link方式打开。3、Universal link方式使用注意事项:࿰…...

Hot Chocolate 构建 GraphQL .Net Core 服务
Hot Chocolate 是 .NET 平台下的一个开源组件库, 您可以使用它创建 GraphQL 服务, 它消除了构建成熟的 GraphQL 服务的复杂性, Hot Chocolate 可以连接任何服务或数据源,并创建一个有凝聚力的服务,为您的消费者提供统一的 API。 我会在 .NET 应用中使用…...

linux shell 入门学习笔记16 流程控制开发
shell的流程控制一般包括if、for、while、case/esac、until、break、continue语句构成。 if语句开发 单分支if //方式1 if <条件表达式> then 代码。。。 fi //方式2 if <条件表达式>;then 代码。。。 fi 双分支if if <条件表达式> then 代码1 if <条件表…...
机器学习:基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测
机器学习:基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测 作者:AOAIYI 作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞…...

给VivoBook扩容重装系统
现在笔记本重装系统都这么复杂吗?原谅我还是10年前的装机水平,折腾了一天终于把系统重新安装好了。 笔记本: ASUS VivoBook 安装系统: Win10 1、扩容 电脑配的512G硬盘满了要换个大的,后盖严丝合缝,不…...

vue 依赖注入使用教程
vue 中的依赖注入,官网文档已经非常详细,笔者在这里总结一份 目录 1、背景介绍 2、代码实现 2.1、依赖注入固定值 2.2、 依赖注入响应式数据 3、注入别名 4、注入默认值 5、应用层 Provide 6、使用 Symbol 作注入名 1、背景介绍 为什么会出现依…...
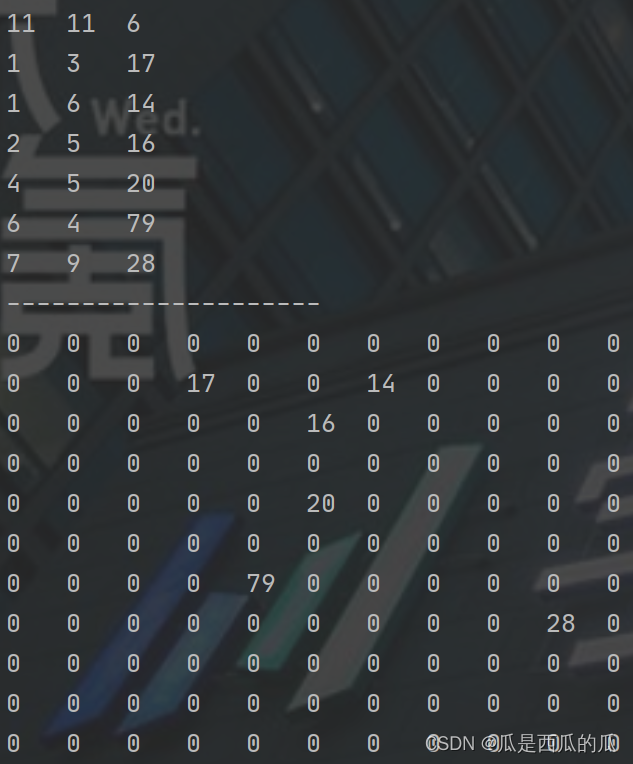
【再临数据结构】Day1. 稀疏数组
前言 这不单单是稀疏数组的开始,也是我重学数据结构的开始。因此,在开始说稀疏数组的具体内容之前,我想先说一下作为一个有着十余年“学龄”的学生,所一直沿用的一个学习方法:3W法。我认为,只有掌握了正确的…...
)
二十四、MongoDB 聚合运算( aggregate )
MongoDB 聚合( aggregate ) 用于处理数据,比如统计平均值,求和等。然后返回计算后的数据结果 MongoDB 聚合有点类似 SQL 语句中的 COUNT( * ) aggregate() 方法 MongoDB aggregate() 为 MongoDB 数据库提供了聚合运算 语法 aggregate() 方法的语法如下 > d…...

【C++】6.模板初阶
交换两个数 任何一个类型交换还要重新写一个函数 如何解决? 模板->写跟类型无关的函数 1.泛型编程 泛型编程:编写与类型无关的通用代码,是代码复用的一种手段。模板是泛型编程的基础。 如何写一个函数适用所有类型的交换? #include &…...

Docker部署Airbyte
Linux环境部署前置要求机器配置2c4g(最低),4c8g(推荐)dockerdocker-compose (要求新版本的docker-compose)安装airbyte,打开终端,进入你想安装airbyte的目录。#Clone代码 git clone https://github.com/air…...

2023王道考研数据结构笔记第一章绪论
第一章 绪论 1.1 数据结构的基本概念 1.数据:数据是信息的载体,是描述客观事物属性的数、字符以及所有能输入到计算机中并被程序识别和处理的符号的集合。 2.数据元素:数据元素是数据的基本单位,通常作为一个整体进行考虑和处理…...

告别空指针让代码变优雅,Optional使用图文例子源码解读
一、前言 我们在开发中最常见的异常就是NullPointerException,防不胜防啊,相信大家肯定被坑过! 这种基本出现在获取数据库信息中、三方接口,获取的对象为空,再去get出现! 解决方案当然简单,只…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
