FLMix: 联邦学习新范式——局部和全局的结合
文章链接:Federated Learning of a Mixture of Global and Local Models
发表期刊(会议): ICLR 2021 Conference(机器学习顶会)
目录
- 1. 背景介绍
- 2. 传统联邦学习
- 3. FL新范式
- 理论逻辑
- 重要假设
- 解的特性
本博客从
优化函数角度出发,学习传统联邦学习 ◊ \Diamond ◊ 和 新型联邦学习 ♣ \clubsuit ♣ 的差异
1. 背景介绍
菲利普和彼得两位学者在阿卜杜拉国王科技大学发表的一篇文章中,对于联邦学习(Federated Learning)和混合专家(MoE)的结合进行了早期的数理讨论。
有意思的是这两位学者的研究动机是为了保护自己的移动设备数据不外露的同时,还可以用这些数据进行机器学习。他们给了两个很简单的理由。
- First, many device users are increasingly sensitive to privacy concerns and prefer their data to never leave their devices.
- Second,moving data from their place of origin to a centralized location is very inefficient in terms of energy and time.
一个理由是不安全,还有一个理由是不方便。
2. 传统联邦学习
目前为止,FL 已经成为一个跨学科领域,专注于通过直接在边缘设备上训练机器学习模型来解决问题。传统的FL框架,每个客户参与FL训练。
参数定义:训练客户数量 N;全局模型结构 M G M_{G} MG;全局模型参数 θ ( d 1 ) 维 \theta (d_{1})维 θ(d1)维
其中 θ ∈ R d 1 \theta \in \mathbb{R}^{d_{1}} θ∈Rd1 and R d 1 ∈ R \mathbb{R}^{d_{1}} \in \mathbb{R} Rd1∈R
FL的学习目标为:
◊ min θ ∈ R d 1 F ( θ ) = 1 N ∑ i = 1 N f i ( θ ) \Diamond \quad \min_{\theta \in \mathbb{R}^{d_{1}}} F(\theta) =\frac{1}{N} \sum_{i=1}^{N} f_{i}(\theta) ◊θ∈Rd1minF(θ)=N1i=1∑Nfi(θ)
对于每一个 f i f_{i} fi,由于数据分布不同,假设第 i i i 个客户的数据分布定义为 D i \mathcal{D} _{i} Di 则:
f i ( θ ) = E ( x , y ) ∼ D i [ f ( x , ξ ) ] f_{i}(\theta)=\mathbb{E}_{(x,y)\sim\mathcal{D}_{i}} [f(x,\xi)] fi(θ)=E(x,y)∼Di[f(x,ξ)]
其中 L i ( ⋅ ) L_{i}(·) Li(⋅)是客户 i i i 的损失函数
求解 F ( θ ) F(\theta) F(θ) 最流行的方法是FedAvg算法,在FedAvg最简单的形式中,即当不使用部分参与、模型压缩或随机近似时,FedAvg缩减为局部梯度下降(LGD)。这是GD在聚合之前对每个设备执行多个梯度步长的扩展。
FedAvg已被证明在经验上是有效的,特别是对于非凸问题(存在多个局部极小值的问题)。但在数据异质时,与非本地对应的算法相比,FedAvg的收敛保证较差。
FL 虽然已经有了诸多理论证明其可行性,但是它的最终结果是全局性的,我们需要思考,对于那些数据异构的个体而言,使用全局方案解决个体问题效用一定好吗?
答案是否定的,数据异构性不仅对设计新的训练方法来解决 ◊ \Diamond ◊ 提出了挑战,而且不可避免地对这种全局解决方案对个人用户的效用提出了质疑。事实上,在所有设备的所有数据中训练的全局模型可能会从个人用户体验的典型数据和使用模式中删除,以至于使其几乎无用。
3. FL新范式
本文提出了一种新的训练联邦学习模型的优化公式。标准
FL旨在从存储在所有参与设备上的私人数据中找到一个单一的全局模型。相比之下,新方法寻求全局模型和局部模型之间的权衡,每个设备可以从自己的私有数据中学习而无需通信。
本文开发了有效的随机梯度下降(SGD)变体来求解新公式,并证明了通信复杂性的保证。该工作的主要贡献包括结合全局和局部模型的FL新范式、新范式的理论性质、无环路局部梯度下降(L2GD)、L2GD的收敛理论以及对局部步骤在联邦学习中的作用的见解。该文件还强调了本地SGD在通信复杂性和个性化联邦学习的好处方面优于传统SGD的潜力。
本文提出的训练监督联邦学习新范式如下:
♣ min x 1 , . . . , x n ∈ R d { F ( x ) : = f ( x ) + λ ψ ( x ) } f ( x ) : = 1 n ∑ i = 1 n f i ( x i ) ψ ( x ) : = 1 2 n ∑ i = 1 n ∥ x i − x ‾ ∥ 2 \clubsuit \quad \min_{x_1,...,x_n \in \mathbb{R}^d } \{ F(x): = f(x)+ \lambda \psi (x)\} \\ f(x):=\frac{1}{n}\sum_{i=1}^{n} f_i(x_i) \\ \psi (x) := \frac{1}{2n}\sum_{i=1}^{n} \left \| x_i-\overline{x} \right \| ^2 ♣x1,...,xn∈Rdmin{F(x):=f(x)+λψ(x)}f(x):=n1i=1∑nfi(xi)ψ(x):=2n1i=1∑n∥xi−x∥2 其中 λ ≥ 0 \lambda \ge0 λ≥0 是一个惩罚超参, x 1 , . . . , x n ∈ R d x_1,...,x_n \in \mathbb{R}^d x1,...,xn∈Rd 是本地模型参数 , x : = ( x 1 , x 2 , . . . , x n ) ∈ R n d x:=(x_1,x_2,...,x_n) \in\mathbb{R}^{nd} x:=(x1,x2,...,xn)∈Rnd 并且 x ‾ : = 1 n ∑ i = 1 n x i \overline{x}:=\frac{1}{n}\sum_{i=1}^{n}x_i x:=n1∑i=1nxi 是所有本地模型的平均值。
文章假设由 f i f_i fi 得到的 F F F 是一个强凸函数。 凸函数是二阶导始终为正(负)的函数,局部最小值即为全局最小值。对于 ◊ \Diamond ◊ 有一个唯一的解。这个解可以表示为:
x ( λ ) : = ( x 1 ( λ ) , . . . , x n ( λ ) ) ∈ R n d x(\lambda ):=(x_1(\lambda),...,x_n(\lambda))\in\mathbb{R}^{nd} x(λ):=(x1(λ),...,xn(λ))∈Rnd接着可以计算 x ‾ ( λ ) : = 1 n ∑ i = 1 n x i ( λ ) \overline{x}(\lambda):=\frac{1}{n}\sum_{i=1}^{n} x_i(\lambda) x(λ):=n1∑i=1nxi(λ)
理论逻辑
所提范式 ♣ \clubsuit ♣ 的理论逻辑:
Local models( λ = 0 \lambda=0 λ=0) :此时模型退化为局部模型,只需要将本地损失降到最低,即求解 min x i ∈ R d f i ( x i ) \min_{x_i \in \mathbb{R}^d } f_i(x_i) xi∈Rdminfi(xi)也就是说, x i ( 0 ) x_i(0) xi(0) 仅基于存储在设备 i i i 上的数据 D i D_i Di 的局部模型。该模型可以由设备 i i i 计算,而无需任何通信。通常情况下, D i D_i Di 不够丰富,无法使用此本地模型。为了学习更好的模型,还必须考虑其他客户的数据。然而,这存在沟通成本。Mixed models( λ ∈ ( 0 , ∞ ) \lambda\in(0,\infty) λ∈(0,∞)):随着 λ \lambda λ 的增加,惩罚 λ ψ ( x ) \lambda \psi (x) λψ(x) 的效果越来越明显,需要沟通以确保模型不会太不相似,否则惩罚 λ ψ ( x ) \lambda \psi (x) λψ(x) 会增大。Global model( λ = ∞ \lambda=\infty λ=∞):现在我们来看 λ → ∞ λ→∞ λ→∞ 的极限情况。直观上,这种极限情况应该迫使最优局部模型之间是相同的,同时最小化损失 f f f,即让 ψ ( x ) → 0 \psi(x) \rightarrow0 ψ(x)→0 。 ψ ( x ) : = 1 2 n ∑ i = 1 n ∥ x i − x ‾ ∥ 2 \psi (x) := \frac{1}{2n}\sum_{i=1}^{n} \left \| x_i-\overline{x} \right \| ^2 ψ(x):=2n1i=1∑n∥xi−x∥2此时,这种情况有一个特殊的极限解: min { f ( x ) : x 1 , . . . , x n ∈ R d , x 1 = ⋯ = x n } \min\{ f(x):x_1,...,x_n\in \mathbb{R}^d ,x_1=\cdots=x_n \} min{f(x):x1,...,xn∈Rd,x1=⋯=xn}。可以反证,如果 λ = ∞ \lambda=\infty λ=∞ 并且 x 1 = x 2 = ⋯ = x n x_1=x_2=\cdots =x_n x1=x2=⋯=xn不成立,那么 F ( x ) = ∞ F(x) = \infty F(x)=∞
重要假设
对于每一个设备 i i i ,它的目标函数 f i : R d → R f_i:\mathbb{R}^d \rightarrow \mathbb{R} fi:Rd→R 是 L − s m o o t h L-smooth L−smooth 并且 μ − s t r o n g l y \mu -strongly μ−strongly 的凸函数。
- L − s m o o t h L-smooth L−smooth:通常用来描述一个函数的平滑程度。一个函数被称为是 L-smooth 的,如果它的一阶导数(梯度)是 Lipschitz 连续的,即梯度的变化受到了一定的约束。
如果存在一个常数 L > 0 L>0 L>0,使得函数 f f f 的梯度 ∇ f ( x ) ∇f(x) ∇f(x) 对于任意的 x x x 和 y y y 满足以下不等式: ∥ ∇ f ( x ) − ∇ f ( y ) ∥ ≤ L ∥ x − y ∥ ∥∇f(x)−∇f(y)∥≤L∥x−y∥ ∥∇f(x)−∇f(y)∥≤L∥x−y∥ ∥ ⋅ ∥ ∥⋅∥ ∥⋅∥ 是向量的范数。这个定义表明函数的梯度变化受到了 L L L 的限制,也就是说在函数曲面上相邻点处的梯度变化是有界的。 - μ − s t r o n g l y \mu -strongly μ−strongly:描述函数的弯曲程度,指的是一个函数在某种程度上比一个凸函数更加强烈地弯曲。如果存在一个常数 μ > 0 \mu>0 μ>0 ,它满足以下不等式: f ( y ) ≥ f ( x ) + ⟨ ∇ f ( x ) , y − x ⟩ + μ 2 ∥ y − x ∥ 2 f(y)≥f(x)+⟨∇f(x),y−x⟩+\frac{μ}{2}∥y−x∥^2 f(y)≥f(x)+⟨∇f(x),y−x⟩+2μ∥y−x∥2 ⟨ ⋅ , ⋅ ⟩ ⟨⋅,⋅⟩ ⟨⋅,⋅⟩ 表示内积运算。这个不等式表明函数 f f f 在任意点 x x x 处的曲率至少为 μ μ μ,即函数图像在局部区域内弯曲程度足够大。
L − s m o o t h L-smooth L−smooth 函数的特性使得在优化问题中的求解更为可行和稳定。因为具有 Lipschitz 连续梯度的函数对于梯度下降等优化算法而言,更容易收敛到局部最优解,避免了梯度变化剧烈导致的震荡或发散。确保收敛
μ − s t r o n g l y \mu -strongly μ−strongly 函数在局部区域内有一个严格的下界,这种特性使得优化算法能够更快速地收敛到全局最优解。加速收敛
解的特性
对于 ♣ \clubsuit ♣ 的最优解,它应该具备以下三个特性:
我们将表征局部和全局的两个函数 f ( x ( λ ) ) f(x(\lambda)) f(x(λ)) 和 ψ ( x ( λ ) ) \psi(x(\lambda)) ψ(x(λ)) 视作关于变量 λ \lambda λ 的函数。
特性一: ψ ( x ( λ ) ) \psi(x(\lambda)) ψ(x(λ)) 是非递增的,对于 ∀ λ > 0 \forall\lambda>0 ∀λ>0 有 ψ ( x ( λ ) ) ≤ f ( x ( ∞ ) ) − f ( x ( 0 ) ) λ ψ(x(λ)) ≤\frac{ f(x(∞))−f(x(0))}{\lambda} ψ(x(λ))≤λf(x(∞))−f(x(0))进一步 f ( x ( λ ) ) f(x(\lambda)) f(x(λ)) 是非递减的,所以 f ( x ( ∞ ) ) ≥ f ( x ( λ ) ) f(x(∞))\ge f(x(\lambda)) f(x(∞))≥f(x(λ)) 。
上述式子表明:随着 λ \lambda λ 的增大,惩罚项 ψ ( x ( λ ) ) ψ(x(λ)) ψ(x(λ)) 会逐渐减少到 0 ,因此最优的局部模型 x i ( λ ) x_i(\lambda) xi(λ) 会随着 λ \lambda λ 的增长越来越相似。同时根据第二种表述, f ( x ( λ ) ) f(x(\lambda)) f(x(λ))随 λ \lambda λ 增加而增加,但不超过标准FL公式的最优全局损耗 f ( x ( ∞ ) ) f(x(∞)) f(x(∞)) 。特性二:对于 ∀ λ > 0 \forall\lambda>0 ∀λ>0 and 1 ≤ i ≤ n 1\le i \le n 1≤i≤n 我们可以得到如下最优局部解表示: x i ( λ ) = x ˉ ( λ ) − 1 λ ∇ f i ( x i ( λ ) ) x_i(λ) = \bar{x}(λ) − \frac{1}{λ}∇f_i(x_i(λ)) xi(λ)=xˉ(λ)−λ1∇fi(xi(λ)) 进一步还有 ∑ i = 1 n ∇ f i ( x i ( λ ) ) = 0 ψ ( x ( λ ) ) = 1 2 λ 2 ∣ ∣ ∇ f ( x ( λ ) ) ∣ ∣ 2 \sum_{i=1}^{n}\nabla f_i(x_i(\lambda))=0 \\ \psi (x(\lambda))=\frac{1}{2\lambda^2}||\nabla f(x(\lambda)) ||^2 i=1∑n∇fi(xi(λ))=0ψ(x(λ))=2λ21∣∣∇f(x(λ))∣∣2从平均模型中减去局部梯度的倍数,可以得到最优局部模型。在最优状态下,局部梯度的总和总是为零。这对 λ = ∞ λ =∞ λ=∞ 显然是正确的,但这对 ∀ λ > 0 \forallλ > 0 ∀λ>0 都不太明显。特性三:最优局部模型以 O ( 1 / λ ) O(1/\lambda) O(1/λ) 的速度收敛于传统的FL解。
令 P ( z ) : = 1 n ∑ i = 1 n f i ( z ) P(z):=\frac{1}{n} {\textstyle \sum_{i=1}^{n}}f_i(z) P(z):=n1∑i=1nfi(z) ,此时 x ( ∞ ) x(\infty) x(∞) 是 P P P 的唯一最小值,可以得到: ∣ ∣ ∇ P ( x ˉ ( λ ) ) ∣ ∣ 2 ≤ 2 L 2 λ ( f ( x ( ∞ ) ) − f ( x ( 0 ) ) ) ||∇P(\bar{x}(λ))||^2 ≤\frac{2L^2}{λ}(f(x(∞)) − f(x(0))) ∣∣∇P(xˉ(λ))∣∣2≤λ2L2(f(x(∞))−f(x(0)))
 ♣ \clubsuit ♣ 的解 x ( λ ) x(λ) x(λ) 到纯局部解 x ( 0 ) x(0) x(0) 和纯整体解 x ( ∞ ) x(∞) x(∞) 的距离是 λ λ λ 的函数。
♣ \clubsuit ♣ 的解 x ( λ ) x(λ) x(λ) 到纯局部解 x ( 0 ) x(0) x(0) 和纯整体解 x ( ∞ ) x(∞) x(∞) 的距离是 λ λ λ 的函数。
相关文章:

FLMix: 联邦学习新范式——局部和全局的结合
文章链接:Federated Learning of a Mixture of Global and Local Models 发表期刊(会议): ICLR 2021 Conference(机器学习顶会) 目录 1. 背景介绍2. 传统联邦学习3. FL新范式理论逻辑重要假设解的特性 本博客从优化函…...
为什么嵌入式没有35岁危机?
为什么嵌入式没有35岁危机? 在当今数字化时代,IT行业变化迅速,技术的更新迭代速度惊人。然而,有一个技术领域却能够在这个竞争激烈的行业中稳步前行,而且不受35岁危机所困扰,那就是嵌入式技术。 嵌入式技术是指将计算…...

PostgreSQL设置主键从1开始自增
和MySQL不同,在 PostgreSQL 中,设置主键从1开始自增并重新开始自增是通过序列(sequence)来实现的。以下是步骤: 步骤1:创建一个序列 CREATE SEQUENCE your_table_id_seqSTART 1INCREMENT 1MINVALUE 1MAXV…...

Vue数据绑定
在我们Vue当中有两种数据绑定的方法 1.单向绑定 2.双向绑定 让我为大家介绍一下吧! 1、单向绑定(v-bind) 数据只能从data流向页面 举个例子: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"…...
js写轮播图,逐步完善
目录 1、自动轮播 2、点击更换 3、自动播放加左右箭头点击切换 4、完整版轮播图 1、自动轮播 用定时器setInterval()来写,可以实现自动播放 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><met…...
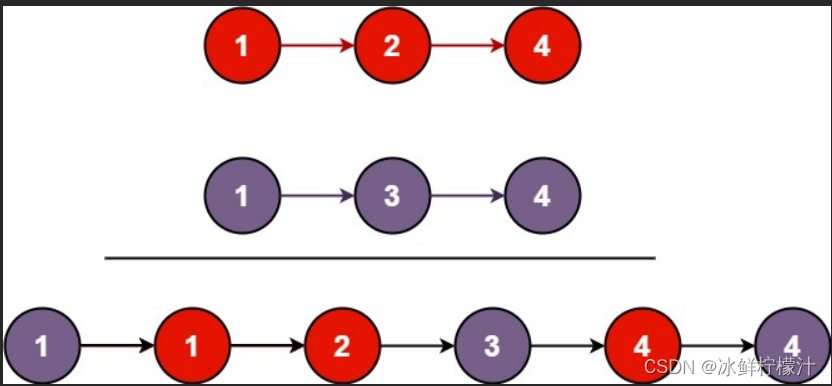
算法-链表-简单-相交、反转、回文、环形、合并
记录一下算法题的学习5 在写关于链表的题目之前,我们应该熟悉回忆一下链表的具体内容 什么是链表: 链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,…...
【500强 Kubernetes 课程】第3章 运行docker容器
一 - 三 ,docker基础操作见 第2章7节 四、docker部署web网站 1、安装 nginx (适合场景:学习 - 略) 2、docker 安装 nginx Stage 1 :docker hub 上 搜索 nginx 镜像 Stage 2:拉取官方镜像 Stage 3&…...

Python中表格插件Tabulate的用法
目录 一、引言 二、Tabulate插件安装与导入 三、Tabulate基本用法 1、创建表格: 2. 格式化表格: 3. 表格转置: 4、合并单元格: 5、指定每列的格式: 6、指定每行的格式: 7、使用自定义表格格式&am…...
)
缺陷分级(过程质量bug分级)
缺陷按照其影响的严重程度,从高到低分成5级,分别为致命(Blocker)、严重(Critical)、一般(Major)、轻微(Minor)以及建议(Enhancement)。…...
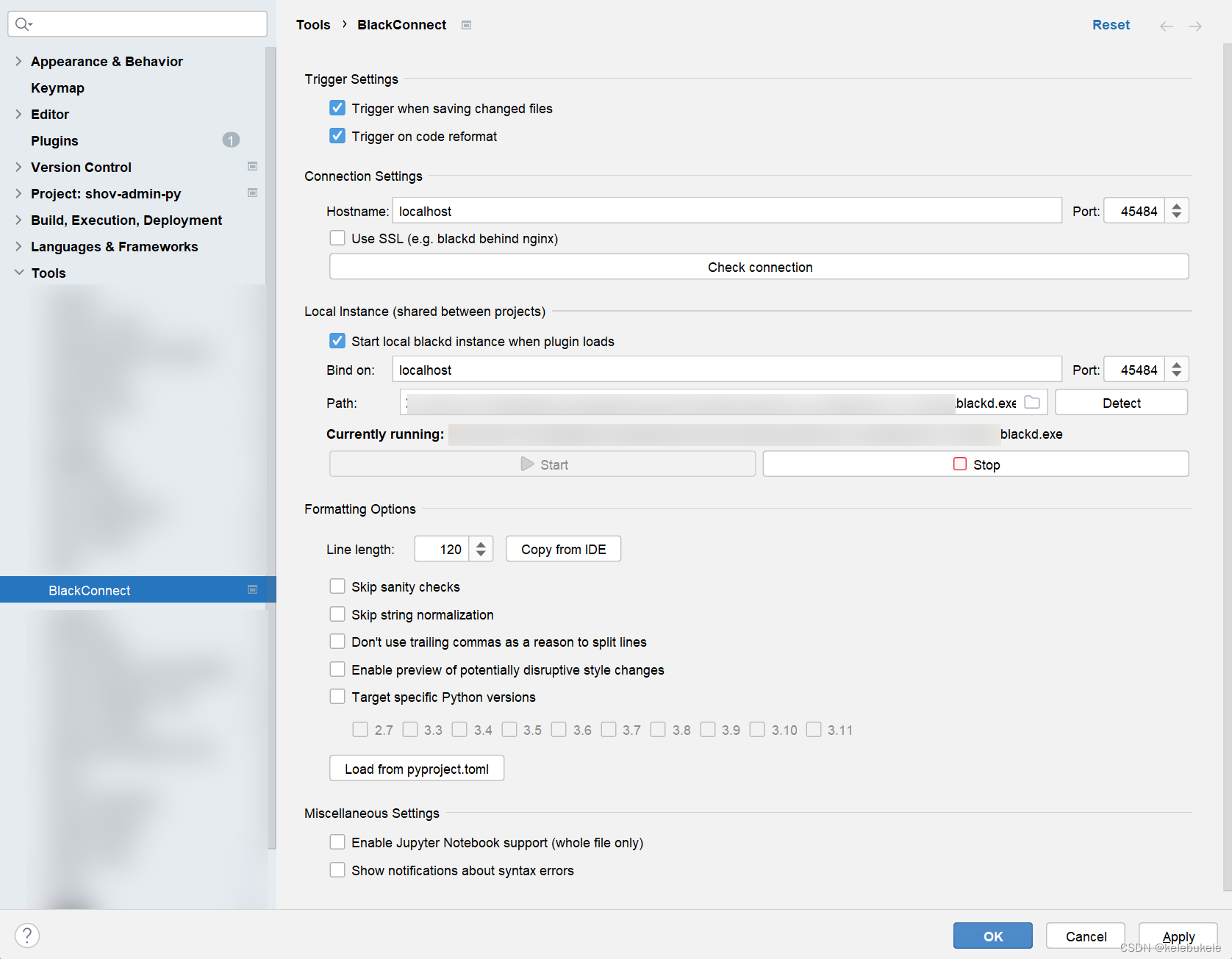
pycharm/vscode 配置black和isort
Pycharm blackd Pycharm中有插件可以实现后台服务运行black:BlackConnect 安装 在python中安装blackd 配置 Pycharm isort pycharm中,isort没有插件,暂使用外部工具实现,外部工具也可添加快捷键实现快捷对文件、文件夹进行fo…...

python列出本地文件路径
按照之前的设想,如果要罗列出本地文件的列表,那不是需要不断的判断文件夹里面的文件夹吗?或者需要使用递归函数本身,才能达到目的吧?没想到使用pop这个函数就可以了。pop是取出元素,那列表里就少了一个&…...

在JavaScript中检查一个数字是否是另一个数字的倍数
使用%模数运算符 为了检查一个数字是否是另一个数字的倍数,我们可以使用JavaScript中的% modulo运算符。 modulo% 操作符返回第一个数字在第二个数字上的余数,例如:10 % 2 0 ,所以如果我们得到一个余数0 ,那么给定的数…...
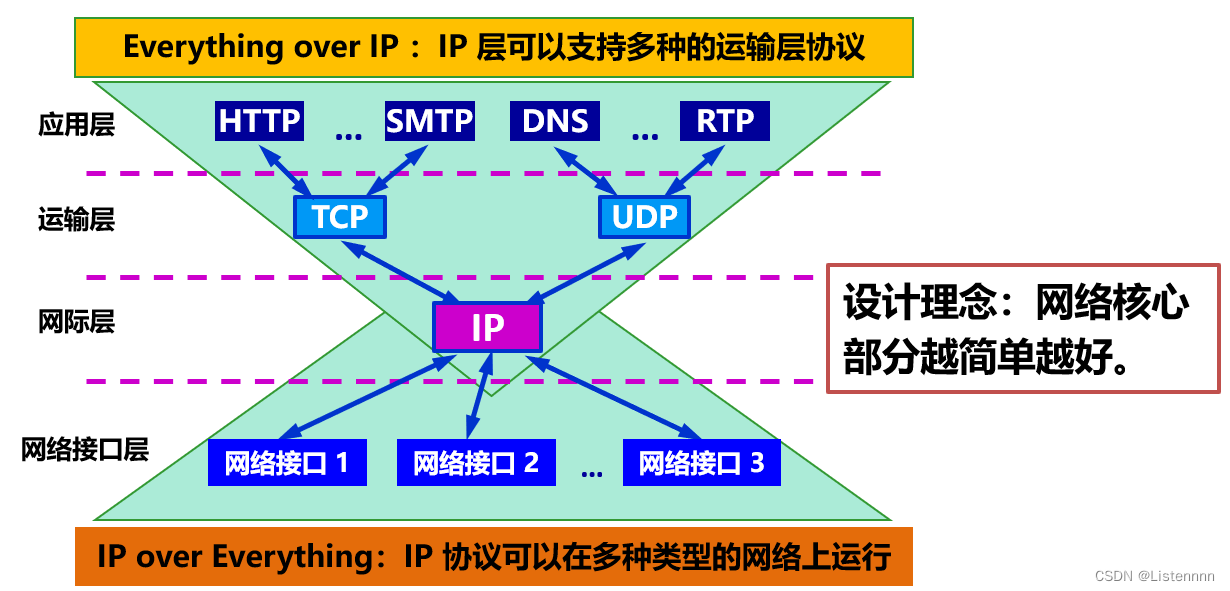
计算机网络五层协议的体系结构
计算机网络中两个端系统之间的通信太复杂,因此把需要问题分而治之,通过把一次通信过程中涉及的所有问题分层归类来进行研究和处理 体系结构是抽象的,实现是真正在运行的软件和硬件 1.实体、协议、服务和服务访问点 协议必须把所有不利条件和…...

MySQL 运算符二
逻辑运算符 逻辑运算符用来判断表达式的真假。如果表达式是真,结果返回 1。如果表达式是假,结果返回 0。 运算符号作用NOT 或 !逻辑非AND逻辑与OR逻辑或XOR逻辑异或 1、与 mysql> select 2 and 0; --------- | 2 and 0 | --------- | 0 | -…...

【SA8295P 源码分析】121 - MAX9295A 加串器芯片手册分析 及初始化参数分析
【SA8295P 源码分析】121 - MAX9295A 加串器芯片手册分析 及初始化参数分析 一、MAX9295A 芯片特性1.1 GPIO 引脚说明1.2 功能模块框图1.3 时序分析1.3.1 GMSL2 Lock Time:25 ms1.3.2 视频初始化延时:1.1ms + 17000 x t(PCLK)1.3.3 High-Speed Data Transmission in Bursts1.…...

问题汇总20231103
文章目录 前言问题汇总1.所有操作系统在CPU层面上是不是都为时间片轮转的形式处理程序?只是任务调度的调度算法不同?那多线程的本质也是时间片吗?只不过很小?2.Mcu和mpu的本质区别3.下载HAL库步骤4.RAM,ROM,SRAM,SDRAM,DDR内存5.编…...

65.Undertow代替Tomcat
SpringBoot中我们既可以使用Tomcat作为Http服务,也可以用Undertow来代替。Undertow在高并发业务场景中,性能优于Tomcat。所以,如果我们的系统是高并发请求,不妨使用一下Undertow,你会发现你的系统性能会得到很大的提升…...

前端mockjs使用方式[express-mockjs]
前提 现在基本上都是前后端分离项目的开发,而前端对于UI界面开发完毕之后往往都需要等待后端的接口提供,因此为了解决这个问题,这里提供一个由express和mockjs结合的本地服务应用项目,可以前端随意造数据配合UI页面进行开发。 个…...

矿区安全检查VR模拟仿真培训系统更全面、生动有效
矿山企业岗位基数大,生产过程中会持续有新入矿的施工人员及不定期接待的参观人员,下井安全须知培训需求量大。传统实景拍摄的视频剪辑表达方式有限,拍摄机位受限,难以生动表达安全须知的内容,且井下现场拍摄光线不理想…...

在SpringBoot中使用EhCache缓存
在使用EhCache缓存之前,我们需要了解的是EhCache缓存是啥? Ehcache的概述 Ehcache是一个开源的Java缓存框架,用于提供高效的内存缓存解决方案,他可以用于缓存各种类型的数据,包括对象,查询结果࿰…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
