2736. 最大和查询 : 从一维限制到二维限制,逐步思考剖析本题(进阶一问)
题目描述
这是 LeetCode 上的 「2736. 最大和查询」 ,难度为 「困难」。
Tag : 「排序」、「离散化」、「树状数组」
给你两个长度为 n、下标从 0 开始的整数数组 nums1 和 nums2,另给你一个下标从 1 开始的二维数组 queries,其中 。
对于第 i 个查询,在所有满足 且 的下标 j ( ) 中,找出 的 最大值 ,如果不存在满足条件的 j 则返回 。
返回数组 answer,其中 answer[i] 是第 i 个查询的答案。
示例 1:
输入:nums1 = [4,3,1,2], nums2 = [2,4,9,5], queries = [[4,1],[1,3],[2,5]]
输出:[6,10,7]
解释:
对于第 1 个查询:xi = 4 且 yi = 1 ,可以选择下标 j = 0 ,此时 nums1[j] >= 4 且 nums2[j] >= 1 。nums1[j] + nums2[j] 等于 6 ,可以证明 6 是可以获得的最大值。
对于第 2 个查询:xi = 1 且 yi = 3 ,可以选择下标 j = 2 ,此时 nums1[j] >= 1 且 nums2[j] >= 3 。nums1[j] + nums2[j] 等于 10 ,可以证明 10 是可以获得的最大值。
对于第 3 个查询:xi = 2 且 yi = 5 ,可以选择下标 j = 3 ,此时 nums1[j] >= 2 且 nums2[j] >= 5 。nums1[j] + nums2[j] 等于 7 ,可以证明 7 是可以获得的最大值。
因此,我们返回 [6,10,7] 。
示例 2:
输入:nums1 = [3,2,5], nums2 = [2,3,4], queries = [[4,4],[3,2],[1,1]]
输出:[9,9,9]
解释:对于这个示例,我们可以选择下标 j = 2 ,该下标可以满足每个查询的限制。
示例 3:
输入:nums1 = [2,1], nums2 = [2,3], queries = [[3,3]]
输出:[-1]
解释:示例中的查询 xi = 3 且 yi = 3 。对于每个下标 j ,都只满足 nums1[j] < xi 或者 nums2[j] < yi 。因此,不存在答案。
提示:
离散化 + 排序 + 树状数组
根据题意,两个等长的数组 num1 和 nums2,只能是相同下标的元素凑成一对。
我们不妨用两个一维数组 nums1 和 nums2 构建出一个二维数组 nums,方便后续处理,其中 。
同时对 queries 进行简单拓展,构建新的二维数组 nq,目的是对原有下标信息进行记录,其中 (此处构建新 nq 的作用,下文会说)。
好了,现在我们有两个新的数组 nums 和 nq,接下来所有讨论都会针对新数组进行。
我希望你牢牢记住:** 是对 nums1 和 nums2 的简单合并;而 是对 queries 原有下标的拓展记录**。
做完简单的预处理工作后,来思考一个前置问题:
假设其他内容不变,要求从满足「 且 」调整为仅需满足「 」,我们会如何求解?
一个简单的做法:
-
对
nums中的第一维(即 )和nq中第一维(即 )排倒序; -
从前往后处理每个询问 ,同时使用变量
idx对nums进行扫描,若满足 时,将idx右移,同时记录已被扫描的数对和 。当
idx不能再后移时,说明当前所有满足 要求的数对已被扫描完,在记录的数对和中取最大值,即是当前询问 的答案 (此处解释了为什么需要构造新数组nq,因为询问处理是按照排序后进行,但在ans中需要映射回原有顺序)。 -
重复步骤 ,直到处理完所有询问。
搞定前置问题后,回到原问题,需要满足「 且 」要求。
进一步思考,排序 + 调整询问顺序,只能解决其中一维限制要求,另一维该如何处理?
或者更加直接的问题:如何在被记录的所有数对和 中找出那些满足 的最大数对和。
不失一般性,假设当前处理到的是 ,其中 的限制要求,通过前置问题的排序方式解决了。另外的 「 我们希望作为“位置信息”,数对和 作为“值信息”进行记录」。
由于条件 ,我们需要对将要作为“位置信息”添加到树状数组的 和 进行离散化,将其映射到 范围内。
对于每个询问,都需要找到已遍历过的大于 的位置上的最大值,把离散化后的值域换成数组坐标,相当于求后缀最大值,后缀最大值可通过相反数,变成求前缀最大值。
能够实现类似的前缀操作,支持“单点修改”和“区间查询”的数据结构是「树状数组」。
Java 代码:
class Solution {
int sz;
int[] tr;
int lowbit(int x) {
return x & -x;
}
void add(int a, int b) {
for (int i = a; i <= sz; i += lowbit(i)) tr[i] = Math.max(tr[i], b);
}
int query(int x) {
int ans = -1;
for (int i = x; i > 0; i -= lowbit(i)) ans = Math.max(ans, tr[i]);
return ans;
}
public int[] maximumSumQueries(int[] nums1, int[] nums2, int[][] queries) {
int n = nums1.length, m = queries.length;
// 构建新的 nums 和 nq
int[][] nums = new int[n][2];
for (int i = 0; i < n; i++) nums[i] = new int[]{nums1[i], nums2[i]};
int[][] nq = new int[m][3];
for (int i = 0; i < m; i++) nq[i] = new int[]{queries[i][0], queries[i][1], i};
// 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
Set<Integer> set = new HashSet<>();
for (int[] x : nums) set.add(x[1]);
for (int[] q : nq) set.add(q[1]);
List<Integer> list = new ArrayList<>(set);
Collections.sort(list);
sz = list.size();
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < sz; i++) map.put(list.get(i), i);
// 调整询问顺序, 解决其中一维限制
Arrays.sort(nums, (a,b)->b[0]-a[0]);
Arrays.sort(nq, (a,b)->b[0]-a[0]);
tr = new int[sz + 10];
Arrays.fill(tr, -1);
int[] ans = new int[m];
int idx = 0;
for (int[] q : nq) {
int x = q[0], y = q[1], i = q[2];
// 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while (idx < n && nums[idx][0] >= x) {
add(sz - map.get(nums[idx][1]), nums[idx][0] + nums[idx][1]);
idx++;
}
ans[i] = query(sz - map.get(y)); // 查询树状数组中的最值
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int sz;
vector<int> tr;
int lowbit(int x) {
return x & -x;
}
void add(int a, int b) {
for (int i = a; i <= sz; i += lowbit(i)) tr[i] = max(tr[i], b);
}
int query(int x) {
int ans = -1;
for (int i = x; i > 0; i -= lowbit(i)) ans = max(ans, tr[i]);
return ans;
}
vector<int> maximumSumQueries(vector<int>& nums1, vector<int>& nums2, vector<vector<int>>& queries) {
int n = nums1.size(), m = queries.size();
// 构建新的 nums 和 nq
vector<vector<int>> nums(n, vector<int>(2));
vector<vector<int>> nq(m, vector<int>(3));
for (int i = 0; i < n; i++) {
nums[i][0] = nums1[i]; nums[i][1] = nums2[i];
}
for (int i = 0; i < m; i++) {
nq[i][0] = queries[i][0]; nq[i][1] = queries[i][1]; nq[i][2] = i;
}
// 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
unordered_set<int> set;
for (auto& x : nums) set.insert(x[1]);
for (auto& q : nq) set.insert(q[1]);
vector<int> list(set.begin(), set.end());
sort(list.begin(), list.end());
sz = list.size();
map<int, int> map;
for (int i = 0; i < sz; i++) map[list[i]] = i;
// 调整询问顺序, 解决其中一维限制
sort(nums.begin(), nums.end(), [](const vector<int>& a, const vector<int>& b) {
return a[0] > b[0];
});
sort(nq.begin(), nq.end(), [](const vector<int>& a, const vector<int>& b) {
return a[0] > b[0];
});
tr.resize(sz + 10, -1);
vector<int> ans(m);
int idx = 0;
for (auto& q : nq) {
int x = q[0], y = q[1], i = q[2];
// 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while (idx < n && nums[idx][0] >= x) {
add(sz - map[nums[idx][1]], nums[idx][0] + nums[idx][1]);
idx++;
}
ans[i] = query(sz - map[y]); // 查询树状数组中的最值
}
return ans;
}
};
Python 代码:
class Solution:
def maximumSumQueries(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:
sz = 0
tr = []
def lowbit(x):
return x & -x
def add(a, b):
i = a
while i <= sz:
tr[i] = max(tr[i], b)
i += lowbit(i)
def query(x):
ans, i = -1, x
while i > 0:
ans = max(ans, tr[i])
i -= lowbit(i)
return ans
n, m = len(nums1), len(queries)
# 构建新的 nums 和 nq
nums = [(nums1[i], nums2[i]) for i in range(n)]
nq = [(queries[i][0], queries[i][1], i) for i in range(m)]
# 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
unique_set = set()
for x in nums:
unique_set.add(x[1])
for q in nq:
unique_set.add(q[1])
unique_list = list(unique_set)
unique_list.sort()
sz = len(unique_list)
mapping = {val: idx for idx, val in enumerate(unique_list)}
# 调整询问顺序, 解决其中一维限制
nums.sort(key=lambda x: x[0], reverse=True)
nq.sort(key=lambda x: x[0], reverse=True)
tr = [-1] * (sz + 10)
ans = [0] * m
idx = 0
for x, y, i in nq:
# 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while idx < n and nums[idx][0] >= x:
add(sz - mapping[nums[idx][1]], nums[idx][0] + nums[idx][1])
idx += 1
ans[i] = query(sz - mapping[y]) # 查询树状数组中的最值
return ans
TypeScript 代码:
function maximumSumQueries(nums1: number[], nums2: number[], queries: number[][]): number[] {
let sz = 0;
let tr = [];
const lowbit = function(x: number): number {
return x & -x;
}
const add = function(a: number, b: number): void {
for (let i = a; i <= sz; i += lowbit(i)) tr[i] = Math.max(tr[i], b);
}
const query = function(x: number): number {
let ans = -1;
for (let i = x; i > 0; i -= lowbit(i)) ans = Math.max(ans, tr[i]);
return ans;
}
const n = nums1.length, m = queries.length;
// 构建新的 nums 和 nq
const nums = Array.from({ length: n }, (_, i) => [nums1[i], nums2[i]]);
const nq = Array.from({ length: m }, (_, i) => [...queries[i], i]);
// 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
const set: Set<number> = new Set();
for (const x of nums) set.add(x[1]);
for (const q of nq) set.add(q[1]);
const list: number[] = [...set];
list.sort((a, b) => a - b);
sz = list.length;
const mapping = new Map();
for (let i = 0; i < sz; i++) mapping.set(list[i], i);
// 调整询问顺序, 解决其中一维限制
nums.sort((a, b) => b[0] - a[0]);
nq.sort((a, b) => b[0] - a[0]);
tr = Array(sz + 10).fill(-1);
const ans = Array(m).fill(0);
let idx = 0;
for (let [x, y, i] of nq) {
// 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while (idx < n && nums[idx][0] >= x) {
add(sz - mapping.get(nums[idx][1])!, nums[idx][0] + nums[idx][1]);
idx++;
}
ans[i] = query(sz - mapping.get(y)!); // 查询树状数组中的最值
}
return ans;
};
-
时间复杂度:令 nums1长度为 ,queries长度为 ,构建nums和nq的复杂度为 ;离散化复杂度为 ;对nums和nq的排序复杂度为 ;构建答案复杂度为 。整体复杂度为 -
空间复杂度:
进阶
本题解讲述了「从一维到二维偏序问题」时,可通过「一维排序,一维树状数组」求通解。
那三维偏序问题呢?是否存在通用的解决思路。
答:一维排序,一维归并,一维树状数组。
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2736 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
相关文章:
)
2736. 最大和查询 : 从一维限制到二维限制,逐步思考剖析本题(进阶一问)
题目描述 这是 LeetCode 上的 「2736. 最大和查询」 ,难度为 「困难」。 Tag : 「排序」、「离散化」、「树状数组」 给你两个长度为 n、下标从 0 开始的整数数组 nums1 和 nums2,另给你一个下标从 1 开始的二维数组 queries,其中 。 对于第…...

2023数维杯国际数学建模A题B题C题D题思路+模型+代码+完整论文
目录 1.数维杯各题思路模型:比赛开始后,第一时间更新,获取见文末名片 3 常见数模问题常见模型分类 3.1 分类问题 3.2 优化问题 详细思路见此名片,开赛第一时间更新 1.数维杯各题思路模型:9.7晚上比赛开始后&#x…...

java多个jar包编译生成.class文件
有时候需要通过多个jar包让java文件生成 .class字节码文件,这里主要记录一下格式问题 javac -cp a.jar;b.jar a.java...

小米手环8pro重新和手机配对解决办法
如果更换了手机,那么小米手环8pro是无法和新手机自动连接的。 但是在新手机上直接连接又连接不上,搜索蓝牙根本找不到手环的蓝牙。 解决办法就是: 把手环恢复出厂!!!!! 是的&…...
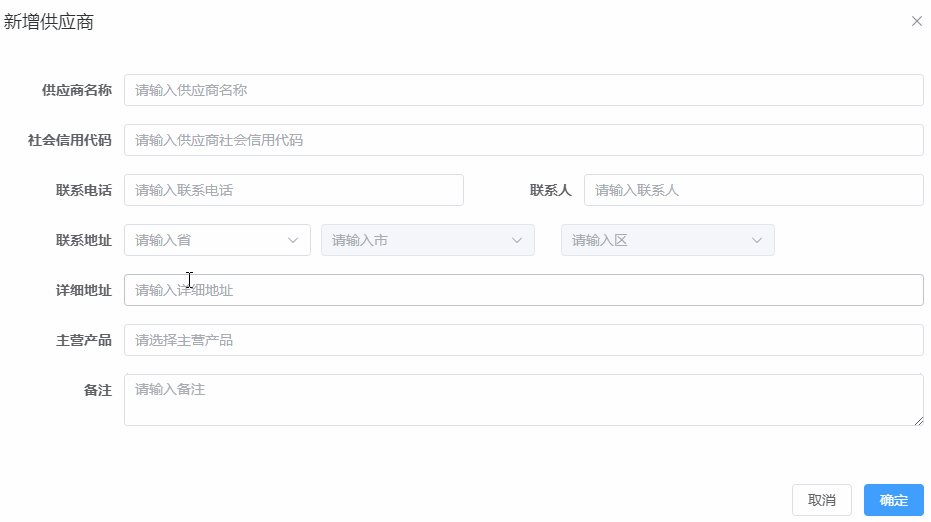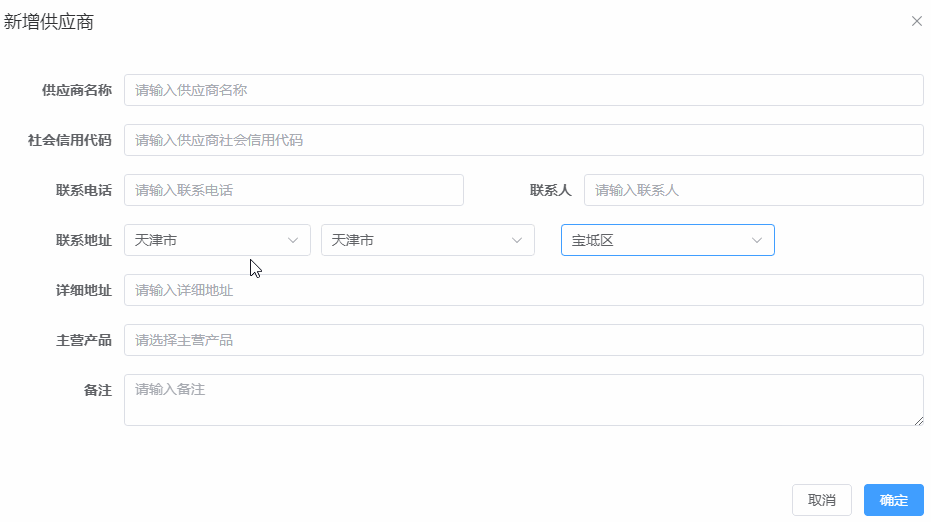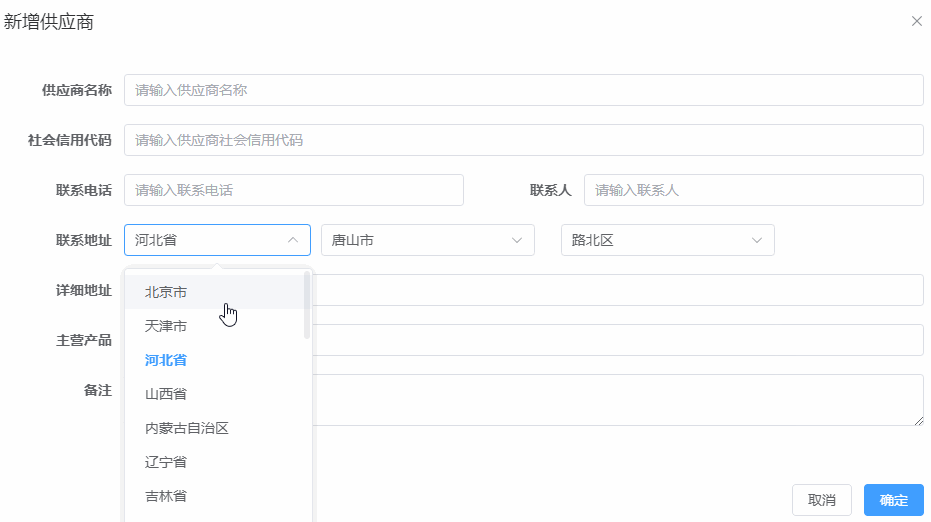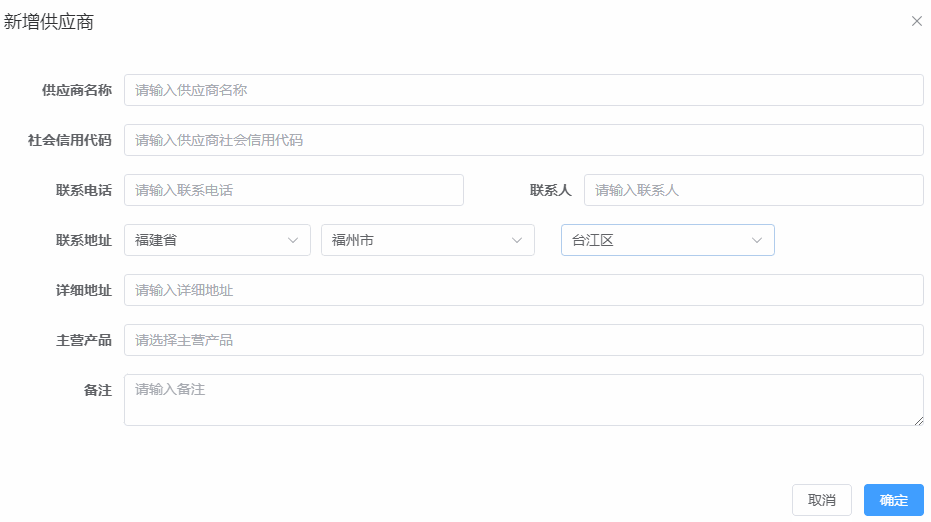
element-china-area-data插件vue3做省市区的下拉选择,用3个独立的el-select实现
第1版,选择下拉没有优化 第2版,选择下拉时,做了优化...

盘点十大免费低/无代码开发软件,数字化转型看这里
在数字化日益普及的当下,低代码开发技术逐渐受到大众的追捧。这种技术让缺乏编程经验的大众也能轻松创建应用程序和网站。通过直观的图形界面和拖拽功能,用户可以无需编写任何代码,轻松实现自己的开发需求。本文将为您介绍十大免费的低代码开…...
【word密码】word设置只读方式的四个方法
想要将word文档设置为只读模式,方法有很多,今天小奥超人介绍几个方法给大家。 方法一:文件属性 常见的、简单的设置方法,不用打开word文件,只需要右键选择文件,打开文件属性,勾选上【只读】选…...

正整数的阶乘
阶乘是基斯顿卡曼(Christian Kramp,1760~1826)于 1808 年发明的运算符号,是数学术语。 一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶…...
微软Surface/Surface pro笔记本电脑进入bios界面
微软Surface笔记本电脑进入bios界面 方法一推薦這種方法:Surface laptop 进BIOS步骤 开机后,不停按音量键进bios界面。 方法二:Surface Book、Surface Pro进bios步骤 1、关闭Surface,然后等待大约10秒钟以确保其处于关闭状态。…...

暂存2暂存2暂存2
暂存2暂存2暂存2...
深入理解TensorFlow:计算图的重要性与应用
TensorFlow是一个流行而强大的机器学习框架,其核心概念之一是计算图(computation graph)。计算图在TensorFlow中扮演着重要角色,作为一种数据流图表示形式,它能够将计算的过程可视化,同时方便优化、分布式计…...

20231114在HP笔记本的ubuntu20.04系统下向RealmeQ手机发送PDF文件
20231114在HP笔记本的ubuntu20.04系统下向RealmeQ手机发送PDF文件 2023/11/14 14:11 手机:Realme Q 笔记本电脑:HP https://item.jd.com/100012583174.html 惠普(HP)战66 三代AMD版 14英寸轻薄笔记本电脑(锐龙7nm 六核…...

【0234】PgBackendStatus 记录当前postgres进程的活动状态
1. 关于PgBackendStatus 每个存活的后端进场在共享内存中维护一个PgBackendStatus结构体,显示其当前活动状态。(结构体是根据BackendId分配的,但这并不重要。) 请注意: 进场状态收集器进程不参与、甚至不访问这些结构。 每个辅助进程还在共享内存中维护一个PgBackendStatu…...

存钱虚拟计划,嘚
存钱计划—虚拟 2024年 (第一年) 1月 2月 3月 4月 5月 6 月 7月 8月 9月 10月 11月 12月 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 2025年(第二年) 1w1w*102.5% A 懒得写A代替 A A A A A A A A A A 2026年(第三年) (1w1w*10…...
基于IDEA进行Maven工程构建
Java全能学习面试指南:https://javaxiaobear.cn 1. 构建概念和构建过程 项目构建是指将源代码、依赖库和资源文件等转换成可执行或可部署的应用程序的过程,在这个过程中包括编译源代码、链接依赖库、打包和部署等多个步骤。 项目构建是软件开发过程中…...
Openssl X509 v3 AuthorityKeyIdentifier实验与逻辑分析
Openssl是X509的事实标准,目前主流OS或个别安全性要求较高的设计场景,对X509的证书链验证已经不在停留在只从数字签名校验了,也就是仅仅从公钥验签的角度,在这些场景中,往往还会校验AuthorityKeyIdentifier和SubjectKe…...

聊聊logback的MDCFilter
序 本文主要研究一下logback的MDCFilter MatchingFilter ch/qos/logback/classic/turbo/MatchingFilter.java public abstract class MatchingFilter extends TurboFilter {protected FilterReply onMatch FilterReply.NEUTRAL;protected FilterReply onMismatch FilterR…...
Windows10安装麒麟桌面V10双系统
概述 想要在Windows10操作系统中安装麒麟V10的桌面操作系统(Kylin-Desktop-V10-Professional-Release-Build1-210203-X86_64) 安装前准备 1、先搞清楚自己的电脑类型 A MBR传统bios单硬盘 B MBR 传统bios双硬盘(SSD固态硬盘机械硬盘&…...

file_put_contents锁的问题
记一次线上生产file_put_contents锁的问题 php项目,很多地方加了日志记录,方法为 function logstr($namelog,$str"",$type"Ymd"){$file date("$type")._.$name..log;$add __DIR__./../runtime/cuslog/.date("Ym&q…...
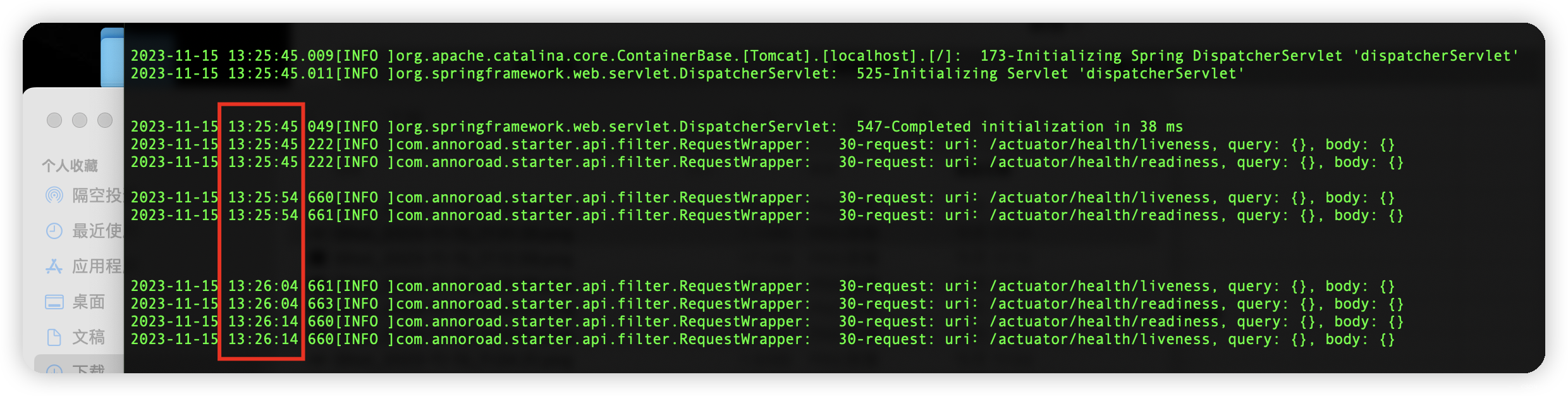
工作中积累的对K8s的就绪和存活探针的一些认识
首先,我的项目是基于 Spring Boot 2.3.5 的,并依赖 spring-boot-starter-actuator 提供的 endpoints 来实现就绪和存活探针,POM 文件如下图: 下面,再让我们来看下与该项目对应的Deployment的YAML文件,如下…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...
