接上一篇 对多个模型环形旋转进行优化 指定旋转位置
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using DG.Tweening;
public class ModelAnimal : MonoBehaviour
{
//记录鼠标滑动
public Vector2 lastPos;//鼠标上次位置
Vector2 currPos;//鼠标当前位置
Vector2 offset;//两次位置的偏移值
//实例化
public static ModelAnimal instance;
//需滑动的物体坐标
public List vertices = new List();
//需滑动的物体
public GameObject[] objArry;
private void Awake()
{
instance = this;for (int i = 0; i < objArry.Length; i++){vertices.Add(objArry[i].transform.localPosition);}
}
void Update()
{DragModel();
}
/// <summary>
/// 拖拽事件
/// </summary>
public void DragModel()
{ if (Input.GetMouseButtonDown(0)){lastPos = Input.mousePosition;Debug.Log(lastPos);}if (Input.GetMouseButtonUp(0)){currPos = Input.mousePosition;offset = currPos - lastPos;Debug.Log(currPos);DoMatch(offset);}
}
/// <summary>
/// 鼠标左滑事件
/// </summary>
public void AnimatorMoveLeft()
{Vector3 finalPos = vertices[objArry.Length - 1];for (int i = objArry.Length - 1; i >= 0; i--){if (1 <= i){objArry[i].transform.DOLocalMove (vertices[i - 1], 2.0f);}else if (0 == i){//objArry[i].transform.localPosition = finalPos;objArry[i].transform.DOLocalMove( finalPos,2.0f);}}GameObject temp = objArry[0];for (int i = 0; i < objArry.Length; i++){if(i < objArry.Length - 1){objArry[i] = objArry[i + 1];}else if(i == objArry.Length - 1){objArry[i] = temp;} }instance.GetComponent<ModelAnimal>().enabled = false;
}/// <summary>
/// 鼠标右滑事件
/// </summary>
public void AnimatorMoveRight()
{ Vector3 Lastpos = vertices[0];for (int i = 0; i <= objArry.Length - 1; i++){if (i < objArry.Length - 1){//objArry[i].transform.localPosition = objArry[i + 1].transform.localPosition;objArry[i].transform.DOLocalMove(vertices[i + 1], 2.0f);}else if (i == objArry.Length - 1){//objArry[i].transform.localPosition = Lastpos;objArry[i].transform.DOLocalMove(Lastpos, 2.0f);} }GameObject temp= objArry[objArry.Length - 1];for (int i = objArry.Length - 1; i >0; i--){ objArry[i] = objArry[i-1];}objArry[0] = temp;instance.GetComponent<ModelAnimal>().enabled = false;
}/// <summary>
/// 移动方向判断
/// </summary>
/// <param name="_offset"></param>
void DoMatch(Vector2 _offset)
{//水平移动if (Mathf.Abs(offset.x) > Mathf.Abs(offset.y)){Debug.Log(offset.x);if (offset.x > 0){Debug.Log("右");AnimatorMoveRight();}else{Debug.Log("左");AnimatorMoveLeft();//sequence.Append(AnimatorMoveLeft());}}else//垂直移动{if (offset.y > 0){Debug.Log("上");}else{Debug.Log("下");}}
}
IEnumerator PlayerAttack()
{yield return new WaitForSeconds(2.0f);Debug.Log("After 2s");
}
}
相关文章:

接上一篇 对多个模型环形旋转进行优化 指定旋转位置
using System.Collections; using System.Collections.Generic; using UnityEngine; using DG.Tweening; public class ModelAnimal : MonoBehaviour { //记录鼠标滑动 public Vector2 lastPos;//鼠标上次位置 Vector2 currPos;//鼠标当前位置 Vector2 offset;//两次位置的偏移…...
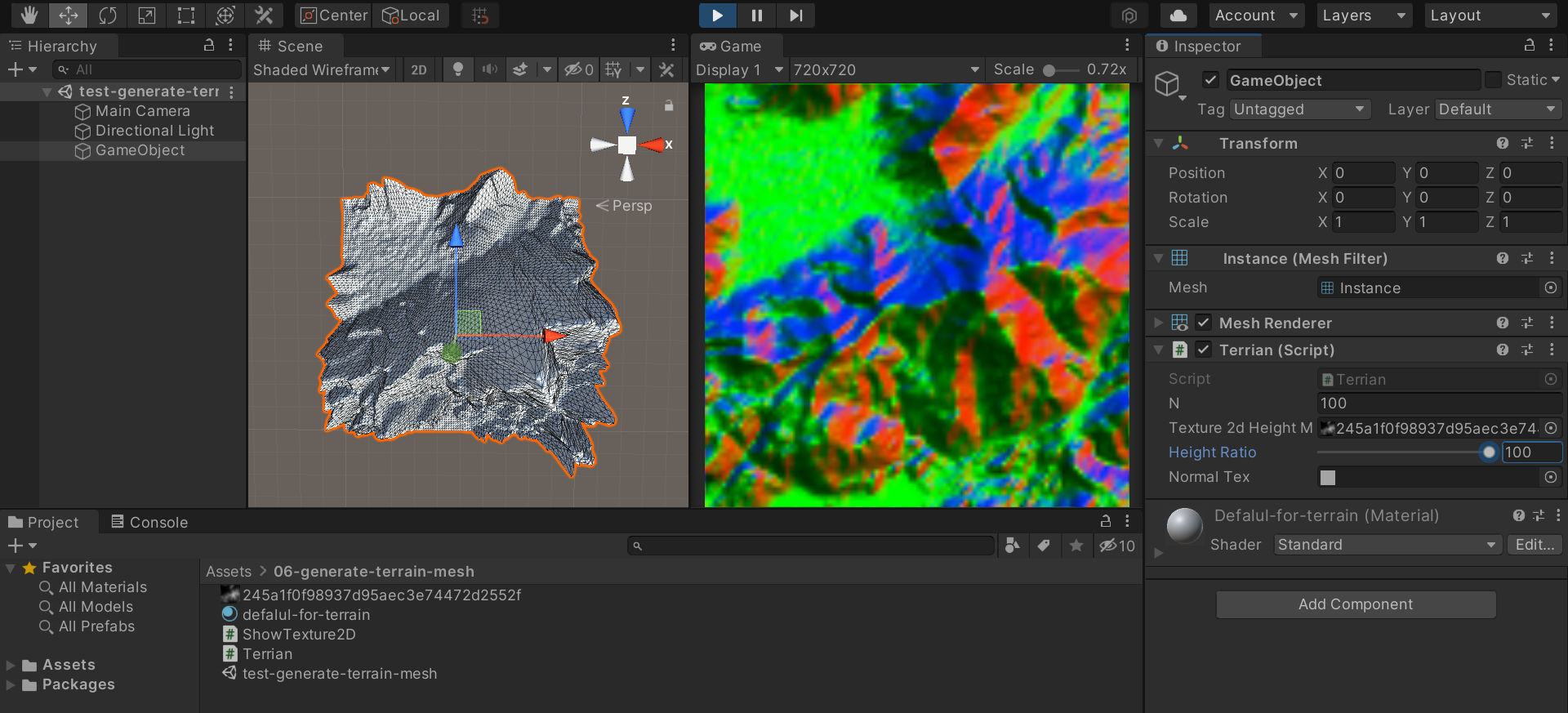
Unity中获取地形的法线
序之前,生成了地形图:(42条消息) 从灰度图到地形图_averagePerson的博客-CSDN博客那末,地形的法线贴图怎么获取?大概分为两个部分吧,先拿到法线数据,再画到纹理中去。关于法线计算Unity - Scripting API: M…...
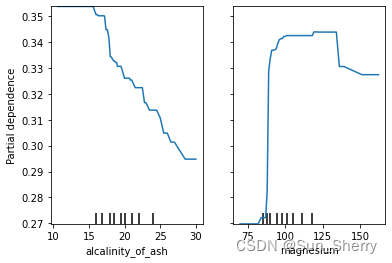
模型解释性:PFI、PDP、ICE等包的用法
本篇主要介绍几种其他较常用的模型解释性方法。 1. Permutation Feature Importance(PFI) 1.1 算法原理 置换特征重要性(Permutation Feature Importance)的概念很简单,其衡量特征重要性的方法如下:计算特征改变后模型预测误差的增加。如果打乱该特征的…...
)
spring常见面试题(2023最新)
目录前言1.spring是什么2.spring的设计核心是什么3.IOC和AOP面试题4.spring的优点和缺点5.spring中bean的作用域6.spring中bean的注入方式7.BeanFactory 和 ApplicationContext有什么区别?8.循环依赖的情况,怎么解决?9.spring中单例Bean是线程…...

华为OD机试题,用 Java 解【压缩报文还原】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
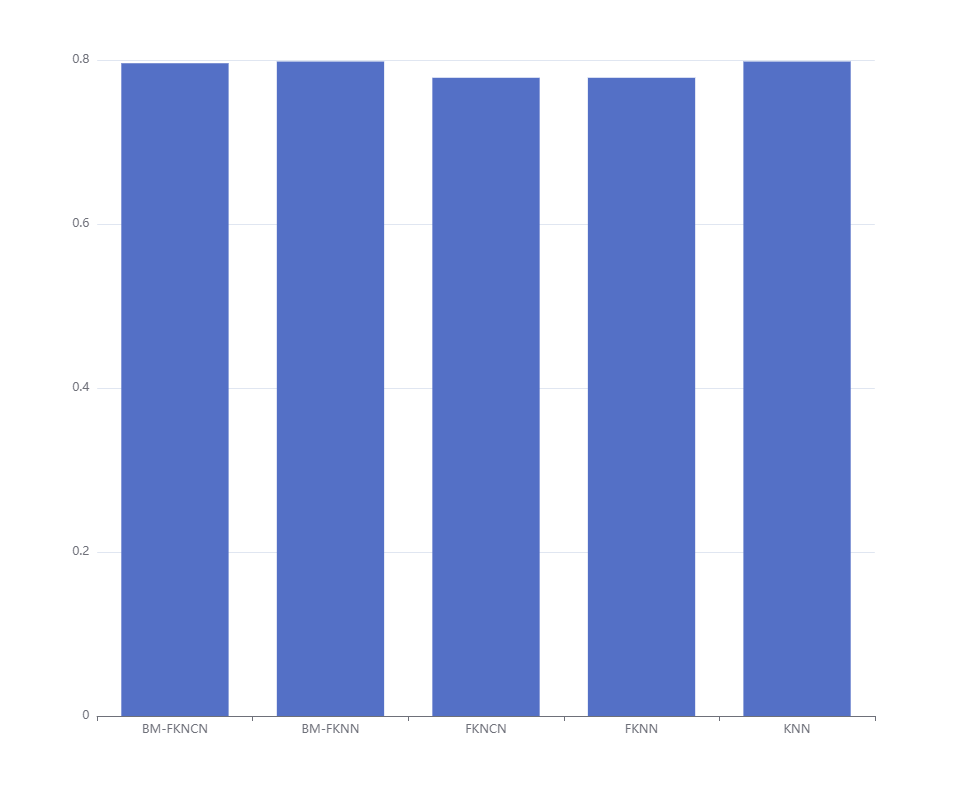
机器学习-BM-FKNCN、BM-FKNN等分类器对比实验
目录 一、简介和环境准备 二、算法简介 2.1四种方法类: 2.1.1FKNN 2.1.2FKNCN 2.1.3BM-FKNN 2.1.3BM-FKNCN 2.2数据预处理 2.3输出视图 2.4调用各种方法看准确率 2.4.1BM-FKNCN 2.4.2BM-FKNN 2.4.3FKNCN 2.4.4FKNN 2.4.5KNN 一、简介和环境准备 k…...

ChatGPT火了,对话式人工智能还能干嘛?
身兼数职的ChatGPT 从2022火到了2023 连日来一直是各大平台的热议对象 其实除了写诗、敲代码、处理文档 以ChatGPT为代表的 对话式人工智能 还有更重要的工作要做 对话式AI与聊天机器人 相信大多数人…...
)
十一、操作数栈的特点(Operand Sstack)
1.每一个独立的栈帧中除了包含局部变量表以外,还包含一个后进先出的操作数栈,也可以称之为表达式栈。 2.操作数栈,在方法执行过程中,根据字节码指令,往栈中写入数据,或提取数据,即入栈ÿ…...

拆解瑞幸新用户激活流程,如何让用户“动”起来?
Aha时刻 一个产品的拉新环节,是多种方式并存的;新用户可能来自于商务搭建了新的渠道,运营策划了新的活动,企划发布了新的广告,销售谈下了新的客户,市场推广了新的群体,以及产品本身的口碑传播,功能更新带来的自然流量。 这是一个群策群力的环节,不同的团队背负不同的K…...
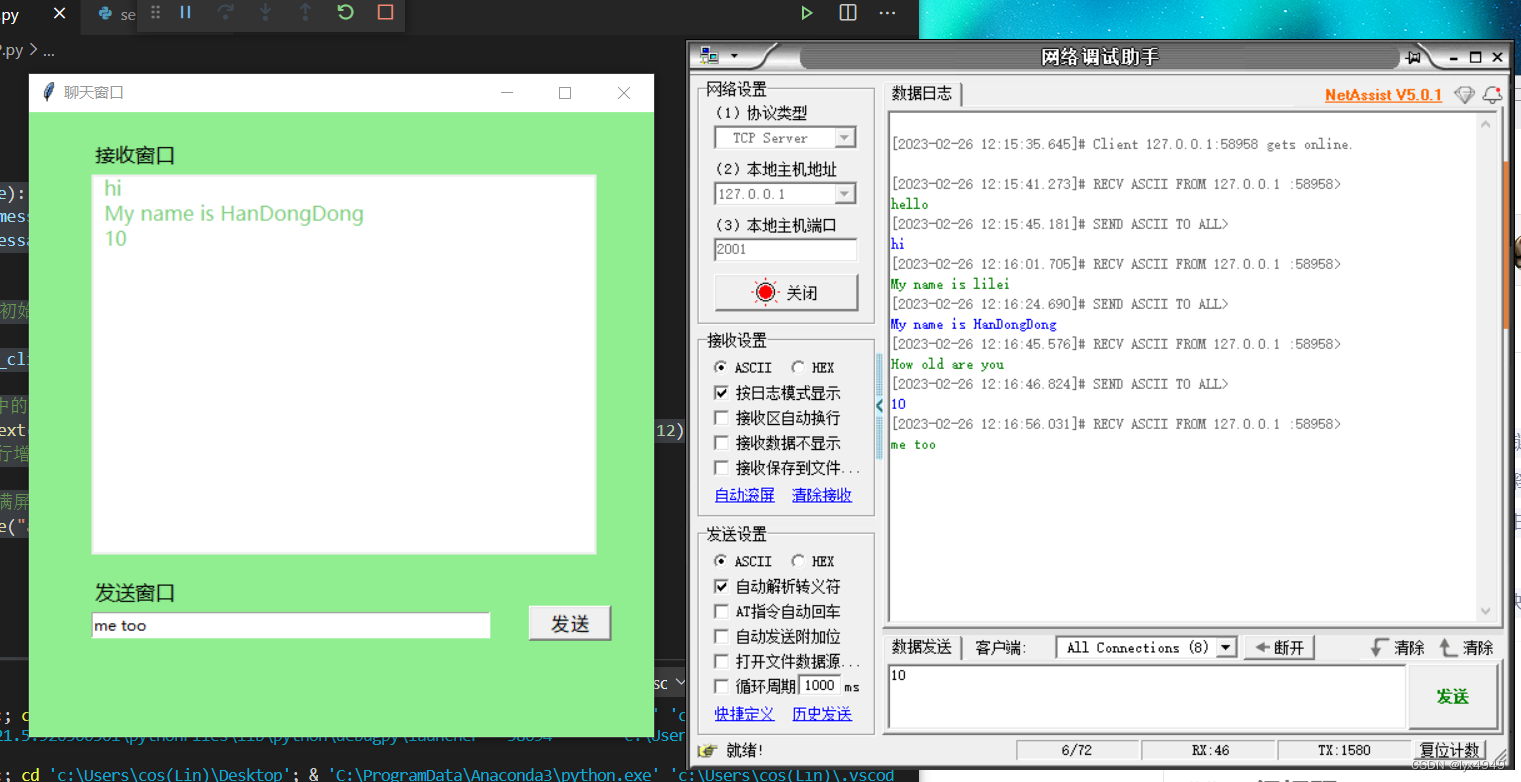
tkinter界面的TCP通信/开启线程等待接收数据
前言 用简洁的语言写一个可以与TCP客户端实时通信的界面。之前做了一个项目是要与PLC进行信息交互的界面,在测试的时候就利用TCP客户端来实验,文末会附上TCP客户端。本文分为三部分,第一部分是在界面向TCP发送数据,第二部分是接收…...

华为OD机试题,用 Java 解【任务混部】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

看linux内核启动流程需要的汇编指令解释
一、指令 0.MRS 和MSR MRS 指令: 对状态寄存器CPSR和SPSR进行读操作。 MSR指令: 对状态寄存器CPSR和SPSR进行写操作。 1.adrp adrp x0, boot_args把boot_args的页基地址提取出来,放到x0中。 2.stp stp x21, x1, [x0]将 x21, x1 的值存入 x0寄存器记录的地址中…...

【巨人的肩膀】JAVA面试总结(二)
1、💪 目录1、💪1.0、什么是面向对象1.1、JDK、JRE、JVM之间的区别1.2、什么是字节码1.3、hashCode()与equals()之间的联系1.4、String、StringBuffer、StringBuilder的区别1.5、和equals方法的区别1.6、重载和重写的区别1.7、List和Set的区别1.8、Array…...

【网络安全入门】零基础小白必看!!!
看到很多小伙伴都想学习 网络安全 ,让自己掌握更多的 技能,但是学习兴趣有了,却发现自己不知道哪里有 学习资源◇瞬间兴致全无!◇ 😄在线找人要资料太卑微,自己上网下载又发现要收费0 🙃差点当…...
)
字节前端经典面试题(附答案)
有哪些可能引起前端安全的问题? 跨站脚本 (Cross-Site Scripting, XSS): ⼀种代码注⼊⽅式, 为了与 CSS 区分所以被称作 XSS。早期常⻅于⽹络论坛, 起因是⽹站没有对⽤户的输⼊进⾏严格的限制, 使得攻击者可以将脚本上传到帖⼦让其他⼈浏览到有恶意脚本的⻚⾯, 其注⼊⽅式很简…...
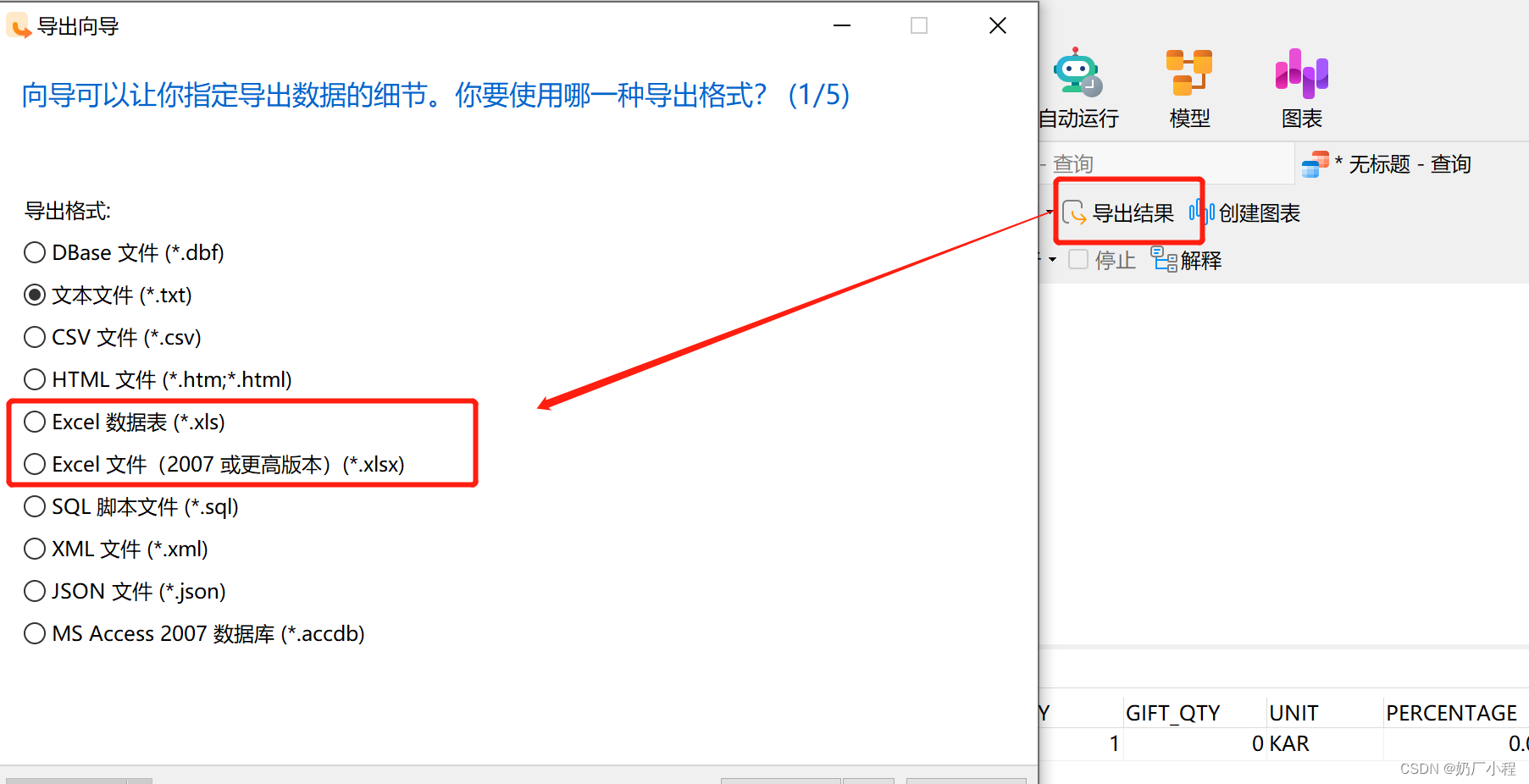
数据库管理工具的使用
目录 摘要 一、Navicat是什么? 二、使用步骤 1.如何下载与安装 2.如何连接远程数据库 总结 摘要 本文主要介绍数据库管理工具的使用 一、Navicat是什么? 它是一款数据库管理工具,将此工具连接数据库,你可以从中看到各种数据库的详细…...

让马斯克反悔的毫米波雷达,被国产雷达头部厂商木牛科技迭代到了5D时代
近日,特斯拉或将在其HW4.0硬件系统配置一枚高精度4D毫米波雷达的消息在外网刷屏。据分析,“纯视觉”信仰者马斯克之所以做出这样的决定,一方面是减配了雷达的特斯拉自动驾驶,表现不尽如人意;另一方面也跟毫米波雷达的技…...
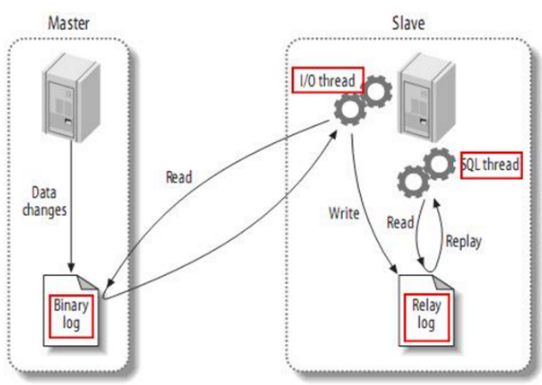
MaxWell原理概述
文章目录1.MaxWell概述2.Maxwell输出数据格式3.Maxwell原理3.1 MySQL二进制日志3.2 MySQL主从复制1.MaxWell概述 Maxwell 是由美国Zendesk公司开源,用Java编写的MySQL变更数据抓取软件。它会实时监控Mysql数据库的数据变更操作(包括insert、update、dele…...
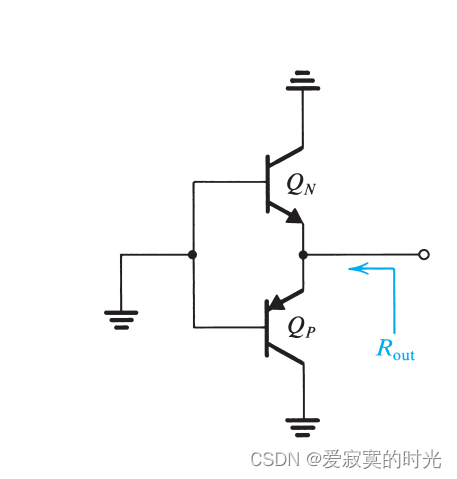
电子技术——AB类输出阶
电子技术——AB类输出阶 原理 交越失真可以通过通过一个较小的偏置电流解除,如下图: QNQ_NQN 和 QPQ_PQP 的基极之间存在偏置电压 VBBV_{BB}VBB 。对于完美匹配的晶体管,当 vI0v_I 0vI0 的时候,此时 vO0v_O 0vO0 。每…...

Archlinux个人安装流程
操作环境: 时间:2023-02-17 电脑型号:联想拯救者R720 cpu:Intel Core i5-7300HQ 4x 3.5GHz gpu:NVIDIA GeForce GTX 1050 Ti 安装系统: 1.下载镜像: 请访问https://archlinux.org/查找镜…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
