【机器学习7】优化算法
1 有监督学习的损失函数
1.1 分类问题
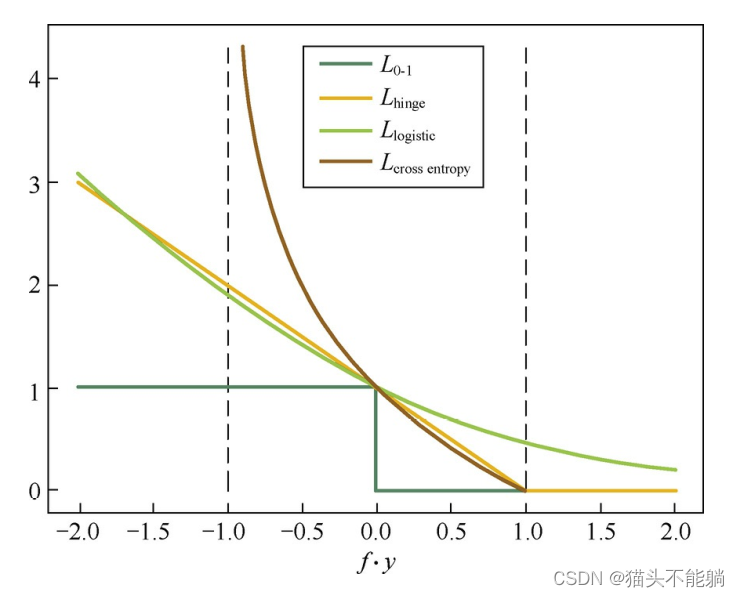
对二分类问题, Y={1,−1}, 我们希望sign f(xi,θ)=yi, 最自然的损失函数是0-1损失,
| 函数定义 | 特点 | |
|---|---|---|
| 0-1损失函数 | 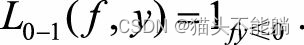 | 非凸、非光滑,很难直接对该函数进行优化 |
| Hinge损失函数 | 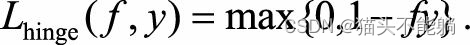 | 当fy≥1时, 该函数不对其做任何惩罚。 Hinge损失在fy=1处不可导, 因此不能用梯度下降法进行优化, 而是用次梯度下降法 |
| Logistic损失函数 |  | 该损失函数对所有的样本点都有所惩罚, 因此对异常值相对更敏感一些 |
| 交叉熵损失函数 | 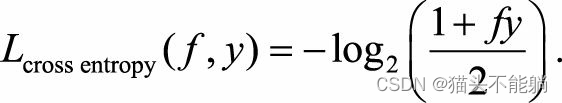 |
1.2回归问题
希望 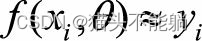 , 最常用的损失函数是平方损失函数
, 最常用的损失函数是平方损失函数
| 函数定义 | 特点 | |
|---|---|---|
| 平方损失函数 | 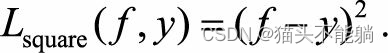 | 对异常点比较敏感 |
| 绝对损失函数 | 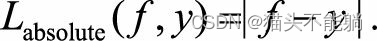 | 在f=y处无法求导数 |
| Huber损失函数 |  | 在 |

2 梯度下降法
梯度下降算法发展过程
3 L1正则化与稀疏性
稀疏性,就是模型中的很多参数为0,相当于对模型进行了特征选择,只留下了重要的特征。提高了模型的泛化能力,降低了过拟合的可能。
为什么L1正则化能让模型具有稀疏性?
3.1 从解空间形状来看

黄色的部分是L2和L1正则项约束后的解空间, 绿色的等高线是凸优化问题中目标函数的等高线,L2正则项约束后的解空间是圆形, 而L1正则项约束的解空间是多边形。显然, 多边形的解空间更容易在尖角处与等高线碰撞出稀疏解。
3.2 从函数叠加来看
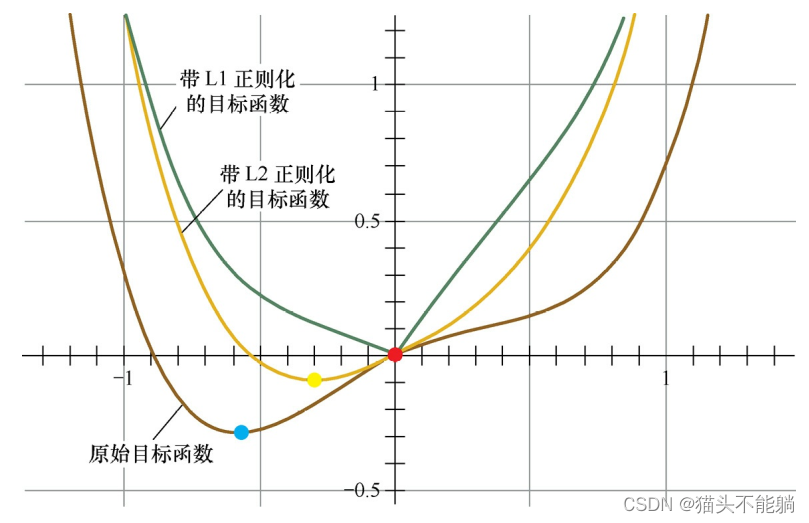
首先, 考虑加上L2正则化项, 目标函数变成L(w)+Cw2, 其函数曲线为黄色。此时, 最小值点在黄点处, 对应的w*的绝对值减小了, 但仍然非0。
然后, 考虑加上L1正则化项, 目标函数变成L(w)+C|w|, 其函数曲线为绿色。此时, 最小值点在红点处, 对应的w是0, 产生了稀疏性。
在一些在线梯度下降算法中, 往往会采用截断梯度法来产生稀疏性, 这同L1正则项产生稀疏性的原理是类似的。
3.3从贝叶斯实验来看
从贝叶斯的角度来理解L1正则化和L2正则化, 简单的解释是, L1正则化相当于对模型参数w引入了拉普拉斯先验, L2正则化相当于引入了高斯先验, 而拉普拉斯先验使参数为0的可能性更大。
相关文章:

【机器学习7】优化算法
1 有监督学习的损失函数 1.1 分类问题 对二分类问题, Y{1,−1}, 我们希望sign f(xi,θ)yi, 最自然的损失函数是0-1损失, 函数定义特点0-1损失函数非凸、非光滑,很难直接对该函数进行优化Hinge损失函数当fy≥1时&…...

常见的近似算法
前言 最近有个项目要用到近似算法,就到处摸了下,整理了一个小结。 近似算法统计 在Java中,你可以使用各种近似算法来解决不精确但接近于最优解的问题。以下是几种常见的近似算法的实现方法: 贪心算法(Greedy Algori…...

【完整详细】IntelliJ IDEA中使用Docker插件一键部署前后端分离项目
前言:在使用Docker部署我们的前后端分离项目的时候,会涉及到一堆且重复的Docker命令,久而久之就会被这些重复性的操作感到繁琐,本篇博客教学大家如何通过IDEA自带的一款插件就可以实现一键部署前后端分离项目的操作,从头到尾我写的非常详细,大家逐步阅读即可。 博主的其他…...

ubuntu20.04 安装TensorRT,解决依赖问题
1.下载Tensor RT对应的deb包 先要确保cuda和cudnn安装好,https://blog.csdn.net/qq_41246375/article/details/115597025 下载tensor RT,注意版本对应关系 https://developer.nvidia.com/nvidia-tensorrt-8x-download 2.安装 按照官方步骤 https://d…...
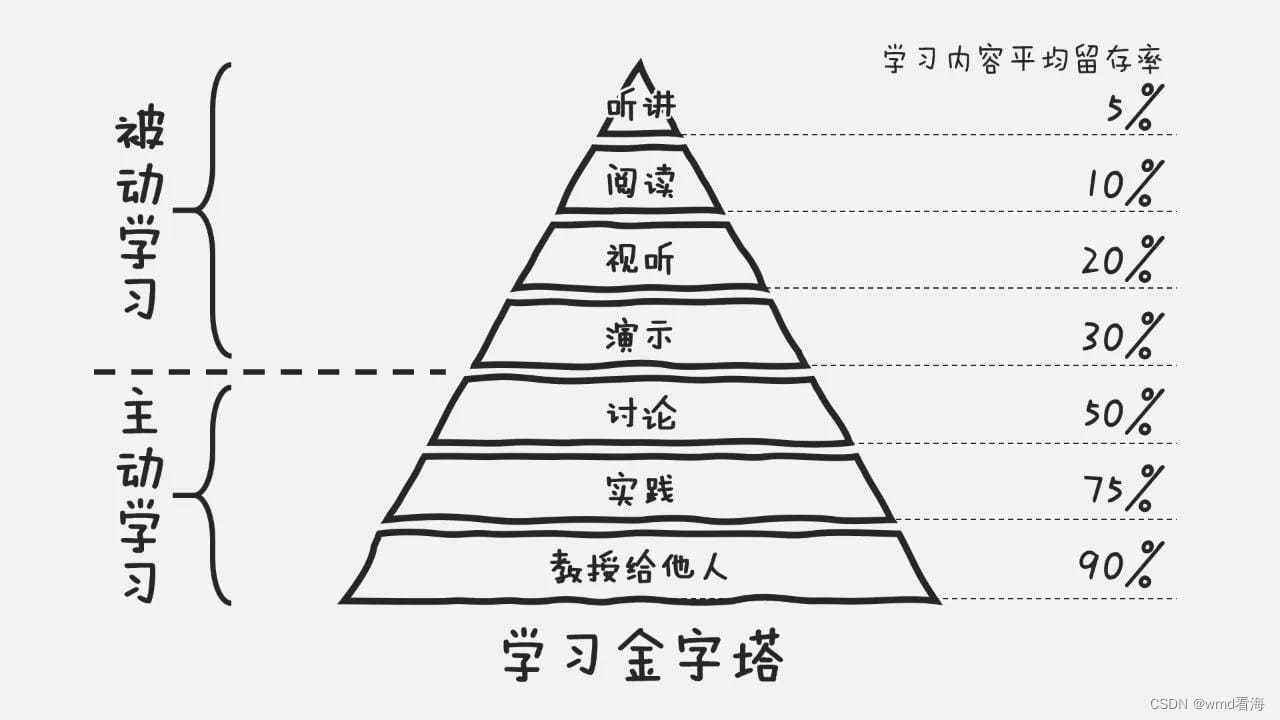
你知道如何科学的学习吗?-关于个人成长的思考
背景 最近在翻看自己工作后的笔记,从有道云笔记到印象笔记,到本地笔记,到自己使用github搭建的博客,到语雀笔记,使用了不同的平台工具;零零总总记录了许多学习笔记、个人成长笔记、职业规划等内容。现在看…...

Java学习之路 —— 多线程
文章目录 1. 线程创建方式1.1 继承Thread1.2 声明一个实现Runnable接口的类1.3 利用Callable接口、FutureTask类来实现 2. 线程同步2.1 同步代码块2.2 同步方法2.3 Lock锁 3. 线程同步4. 线程池 1. 线程创建方式 1.1 继承Thread 定义子类,继承Thread,创…...
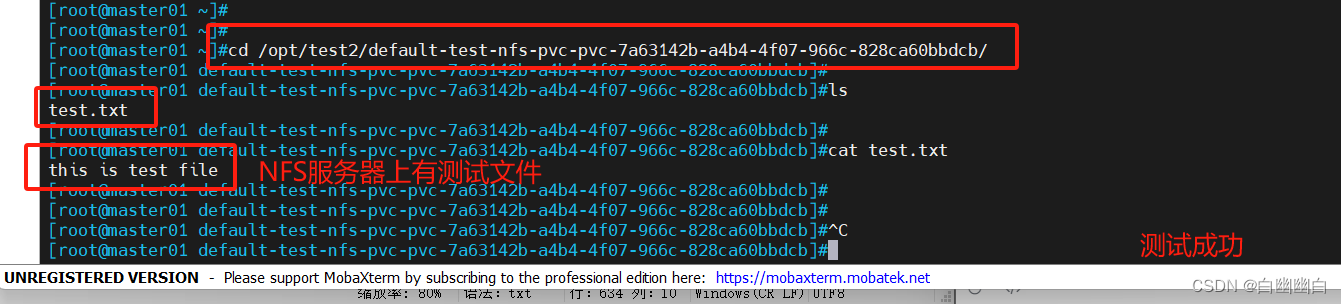
【云原生-Kurbernetes篇】K8s的存储卷/数据卷+PV与PVC
这是一个目录标题 一、Kurbernetes中的存储卷1.1 为什么需要存储卷?1.2 存储卷概述1.2.1 简介1.2.2 volume字段 1.3 常用的存储卷类型1.3.1 emptyDir(临时存储卷)1.3.2 hostPath(节点存储卷)1.3.3 nfs1.3.4 cephfs 二、…...

二层、三层交换机之间到底有什么区别?
简单地说 二层交换机,没有充当三层网关角色的能力(Capability)。三层交换机,首先也是二层交换机。但是,它有一个额外的能力(Capability),软件配置一下,可以充当三层网关…...
【论文阅读】2736. 最大和查询-2023.11.17
题目: 2736. 最大和查询 给你两个长度为 n 、下标从 0 开始的整数数组 nums1 和 nums2 ,另给你一个下标从 1 开始的二维数组 queries ,其中 queries[i] [xi, yi] 。 对于第 i 个查询,在所有满足 nums1[j] > xi 且 nums2[j]…...

2. zk集群部署
简介 上一篇文章我们已经把环境准备好了,jdk也配置好了,下面我们开始把zk部署起来 hadoop环境准备 创建zk用户 useradd zk -d /home/zk echo "1q1w1e1r" | passwd --stdin zk上传zk包 拷贝zk包到/home/zk目录,这里的zk版本为 3.6.3 scp…...

抖音快手判断性别、年龄自动关注脚本,按键精灵开源代码!
这个是支持抖音和快手两个平台的,可以进入对方主页然后判断对方年龄和性别,符合条件的关注,不符合条件的跳过下一个ID,所以比较精准,当然你可以二次开发加入更多的平台,小红书之类的,仅供学习&a…...
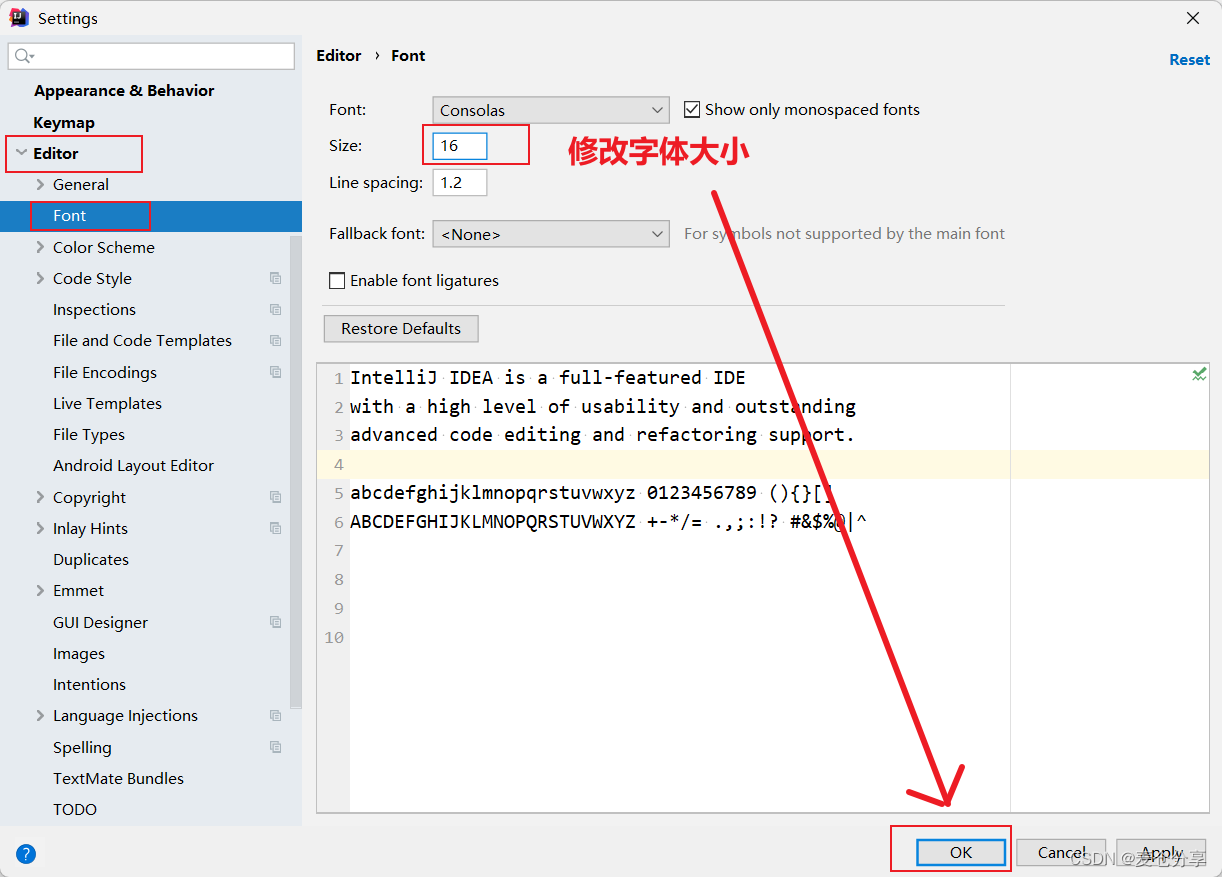
IDEA软件使用步骤
1.IDEA概述 IDEA全称InelliJ IDEA,是用于java语言开发的集成环境,它是业界公认的目前用于Java程序开发最好的工具。 集成环境:把代码编写,编译,执行,调试扽过多种功能综合到一起的开发工具。 下载:https…...
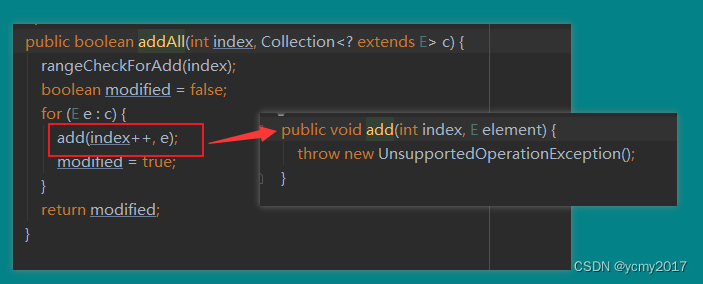
设计模式-11-模板模式
经典的设计模式有23种,但是常用的设计模式一般情况下不会到一半,我们就针对一些常用的设计模式进行一些详细的讲解和分析,方便大家更加容易理解和使用设计模式。 1-什么是模板模式 模板模式,全称是模板方法设计模式,英…...
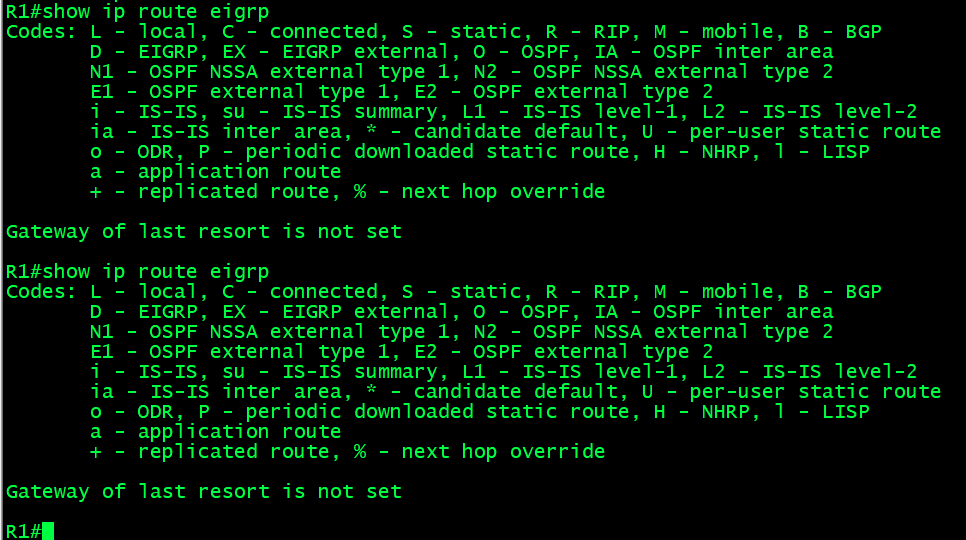
【技术分享】EIGRP stub实验
【赠送】IT技术视频教程,白拿不谢!思科、华为、红帽、数据库、云计算等等https://xmws-it.blog.csdn.net/article/details/117297837?spm1001.2014.3001.5502【微/信/公/众/号:厦门微思网络】 拓扑图: R1配置: route…...

Python 爬虫 AES DES加密反爬
当你遇到需要处理 AES 或 DES 加密的反爬虫机制时,Python 可以通过使用相应的库来解决这类问题。首先,我们需要理解 AES 和 DES 加密是什么: AES (Advanced Encryption Standard):一种广泛使用的对称加密算法,它使用相…...

(论文阅读30/100)Convolutional Pose Machines
30.文献阅读笔记CPMs 简介 题目 Convolutional Pose Machines 作者 Shih-En Wei, Varun Ramakrishna, Takeo Kanade, and Yaser Sheikh, CVPR, 2016. 原文链接 https://arxiv.org/pdf/1602.00134.pdf 关键词 Convolutional Pose Machines(CPMs)…...
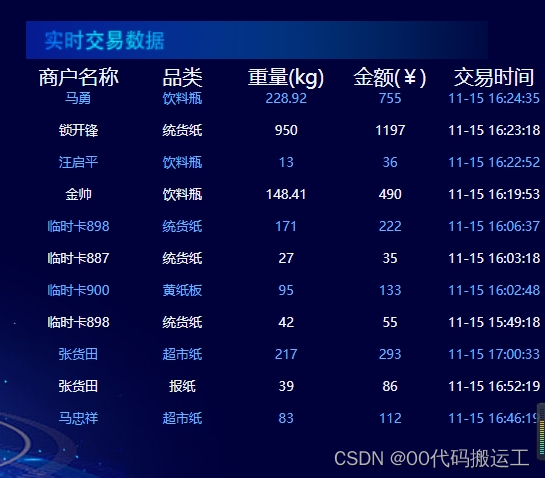
vue3实现数据大屏内数据向上滚动,鼠标进入停止滚动 vue3+Vue3SeamlessScroll
1.效果图 2.npm下载依赖及main.js文件配置 npm install vue3-seamless-scroll --saveimport vue3SeamlessScroll from vue3-seamless-scroll;app.use(vue3SeamlessScroll) 3.html代码 <!-- scrollFlag为true时再渲染,vue3只要涉及到传值子页面需要加flag判断,否…...

WPF显示3D图形
C# 中的 WPF (Windows Presentation Foundation) 支持显示3D图形。WPF 使用 DirectX 作为底层图形引擎,这意味着它可以处理包括3D图形在内的复杂渲染任务。 在 WPF 中,你可以使用一些内置的类和控件来创建和显示3D对象。这包括 Viewport3D, Camera, Mod…...

Xrdp+Cpolar实现远程访问Linux Kali桌面
XrdpCpolar实现远程访问Linux Kali桌面 文章目录 XrdpCpolar实现远程访问Linux Kali桌面前言1. Kali 安装Xrdp2. 本地远程Kali桌面3. Kali 安装Cpolar 内网穿透4. 配置公网远程地址5. 公网远程Kali桌面连接6. 固定连接公网地址7. 固定地址连接测试 前言 Kali远程桌面的好处在于…...

赚钱
《赚钱》 作者/罗光记 赚钱劳身影未安, 岁月匆匆易逝难。 银钱到手笑颜开, 酒醉灯昏影独寒。 花前月下欢声起, 万金财富待来年。 诗酒飘香梦中笑, 人生何求更多钱。...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
