常见的数据结构有哪些?
数据结构分为逻辑结构和物理结构。
- 逻辑结构:指数据元素之间逻辑关系的数据结构,这里的逻辑关系是指数据元素之间的前后间关系,与数据在计算机中的存储位置无关。
- 物理结构:指数据的逻辑结构在计算机存储空间中的存放形式称为数据的物理结构,也叫做存储结构。
数据的逻辑结构主要分为线性结构和非线性结构。
- 线性结构:数据结构的元素之间存在一对一线性关系,所有结点都最多只有一个直接前趋结点和一个直接后继结点。常见的有数组、队列、链表、栈。
- 非线性结构:各个结点之间具有多个对应关系,一个结点可能有多个直接前趋结点和多个直接后继结点。常见的有多维数组、广义表、树结构和图结构等。
数据的物理结构(以后我都统一称存储结构),表示数据元素之间的逻辑关系,一种数据结构的逻辑结构根据需要可以表示成多种存储结构,常用的存储结构有:
- 顺序存储:存储顺序是连续的,在内存中用一组地址连续的存储单元依次存储线性表的各个数据元素。
- 链式存储:在内存中的存储元素不一定是连续的,用任意地址的存储单元存储元素,元素节点存放数据元素以及通过指针指向相邻元素的地址信息。
- 索引存储:除建立存储结点信息外,还建立附加的索引表来标识节点的地址。索引表由若干索引项组成。
- 散列存储:又称Hash存储,由节点的关键码值决定节点的存储地址。
常用的数据结构
- 数组(Array)
- 队列(Queue)
- 链表(Linked List)
- 栈(Stack)
- 树(Tree)
- 散列表(Hash)
- 堆(Heap)
- 图(Graph)
相关文章:

常见的数据结构有哪些?
数据结构分为逻辑结构和物理结构。 逻辑结构:指数据元素之间逻辑关系的数据结构,这里的逻辑关系是指数据元素之间的前后间关系,与数据在计算机中的存储位置无关。物理结构:指数据的逻辑结构在计算机存储空间中的存放形式称为数据…...

Spring中有哪几种方法获取HttpSession对象
Spring MVC 可以直接作为Controller的参数传入: RequestMapping(value "/test", method RequestMethod.POST, produces "application/json;charsetUTF-8")ResponseBodypublic Map test(HttpSession session, String otherParam) {//TODOre…...

springboot开启Redis缓存支持
开启缓存支持,只需要继承CachingConfigurerSupport 即可。代码如下: import com.fasterxml.jackson.annotation.JsonAutoDetect; import com.fasterxml.jackson.annotation.PropertyAccessor; import com.fasterxml.jackson.databind.ObjectMapper; impo…...

2.4 矩阵的运算法则
矩阵是数字或 “元素” 的矩形阵列。当矩阵 A A A 有 m m m 行 n n n 列,则是一个 m n m\times n mn 的矩阵。如果矩阵的形状相同,则它们可以相加。矩阵也可以乘上任意常数 c c c。以下是 A B AB AB 和 2 A 2A 2A 的例子,它们都是 …...

让文字在盒子中水平居中与垂直居中
简单方法: 1.先用text-align: center;将文字垂直居中。 2.再用line-height: Xpx;将元素的行高设置为与父元素同样的高度。(这里的X代表父元素的高度) 举例: 对于该网页的代码如下: <!DOCTYPE html> <html&…...

聊一聊前端面临的安全威胁与解决对策
前端是用户在使用您的网站或Web应用程序时首先体验到的东西。如果您的Web应用程序的前端受到侵害,它可能会影响整个布局,并造成糟糕的用户体验,可能难以恢复。集成前端安全变得越来越重要,本文将指导您通过可以应用于保护您的Web应…...

【matlab学习】现代控制
文章目录 (1) SISO Modeling(2) MIMO Modeling(3) 状态空间模型(4) 状态空间模型->传递函数(5) 传递函数->状态空间模型(6) 状态空间模型变换(7) 特征值和特征向量(8) 广义特征向量(9) 状态空间模型->约旦型 (1) SISO Modeling y ( k 2 ) 5 y ( k 1 ) 6 y ( k ) …...

Debezium报错处理系列之九十九:ConnectException: Source offset ‘file‘ parameter is missing
Debezium报错处理系列之九十九:ConnectException: Source offset file parameter is missing 一、完整报错二、错误原因三、解决方法研究Debezium技术遇到的各种错误解决方法系列文章传送门: Debezium从入门到精通系列之:百篇系列文章汇总之研究Debezium技术遇到的各种错误的…...

基于深度学习的活体人脸识别检测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1. 活体人脸识别检测算法概述 4.2. 深度学习在活体人脸识别检测中的应用 4.3. 算法流程 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 MATLAB2022a 3.部分核心程序 …...
Angular 由一个bug说起之二:trackBy的一点注意事项
trackBy是angualr优化项目性能的一种方法, 通过返回一个具有绑定性的唯一值, 比如id,手机号,身份证号之类的,来让angular能够跟踪数组的项目,根据数据的变化来重新生成DOM, 这样就节约了性能。 但是如果是使用ngFor循环组件&…...
单片机FLASH下载算法的制作
环境 硬件使用正点原子STM32F407探索者V2开发板 编程环境使用MDK 下载工具使用JLINK FLASH芯片使用W25Q128 什么是下载算法 单片机FLASH的下载算法是一个FLM文件,FLM通过编译链接得到,其内部包含一系列对FLASH的操作,包括初始化、擦除、写…...

[nlp] 损失缩放(Loss Scaling)loss sacle
在深度学习中,由于浮点数的精度限制,当模型参数非常大时,会出现数值溢出的问题,这可能会导致模型训练不稳定。为了解决这个问题,损失缩放(Loss Scaling)技术被引入,它通过缩放损失值来解决这个问题。 在深度学习中,损失缩放技术通常是通过将梯度进行缩放来实现的。具…...

Django框架之视图层
【一】三板斧 【1】HttpResponse 返回字符串类型 【2】render 返回html页面,并且在返回给浏览器之前还可以给html页面传值 【3】redirect 重定向页面 在视图文件中写视图函数的时候不能没有返回值了,默认返回的是None,页面上就会报错 d…...
商城免费搭建之java商城 java电子商务Spring Cloud+Spring Boot+mybatis+MQ+VR全景+b2b2c
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...

AI机器学习实战 | 使用 Python 和 scikit-learn 库进行情感分析
专栏集锦,大佬们可以收藏以备不时之需 Spring Cloud实战专栏:https://blog.csdn.net/superdangbo/category_9270827.html Python 实战专栏:https://blog.csdn.net/superdangbo/category_9271194.html Logback 详解专栏:https:/…...
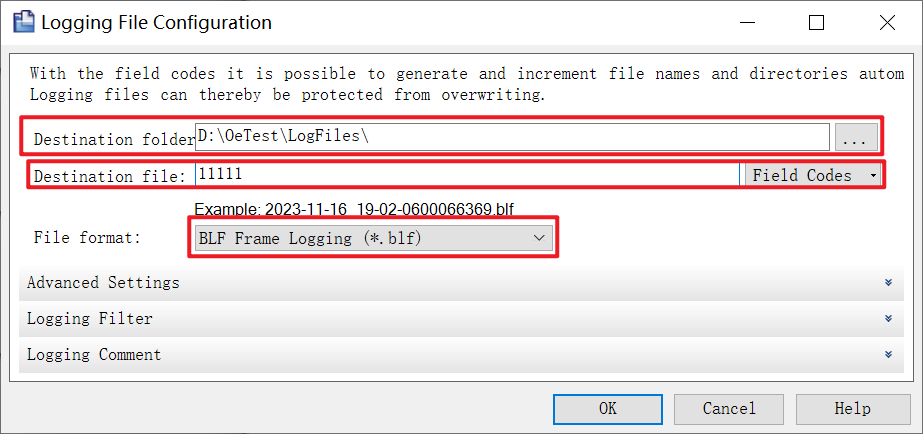
CANoe-Logging模块如何抓取总线数据
在CANoe测量期间(CANoe运行时),总线数据经由Measurement Setup界面的各分析模块的输入口流入Trace、Graphics、Data等窗口中,或统计、或显示、或分析。总线数据除了能流入分析窗口中做解析外,还可以保存到log文件中,留作其他人分析或复现的文件。 在Measurement Setup界…...
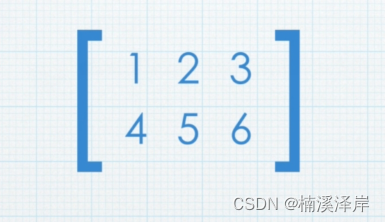
Unity中Shader的矩阵加减法
文章目录 前言一、什么是矩阵矩阵就是一组数的阵列 二、矩阵的加法三、矩阵的负值四、矩阵的减法五、矩阵的表示 前言 Unity中Shader用到的矩阵加减法,以及矩阵的一些基础常识 一、什么是矩阵 矩阵就是一组数的阵列 1 2 3 4 5 6 二、矩阵的加法 两个矩阵相加就是…...
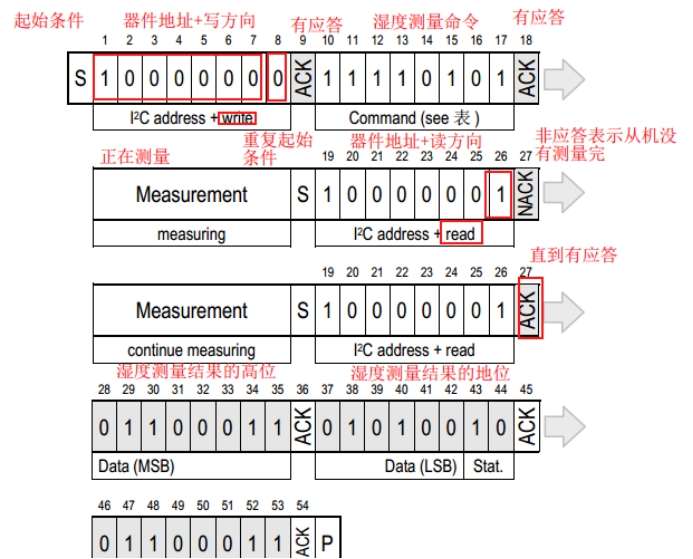
IIC总线概述和通信时序代码详细图文解析
IIC总线 1 IIC总线概述 I2C总线两线制包括:串行数据SDA(Serial Data)、串行时钟SCL(Serial Clock)。总线必须由主机(通常为微控制器)控制,主机产生串行时钟(SCL&#x…...
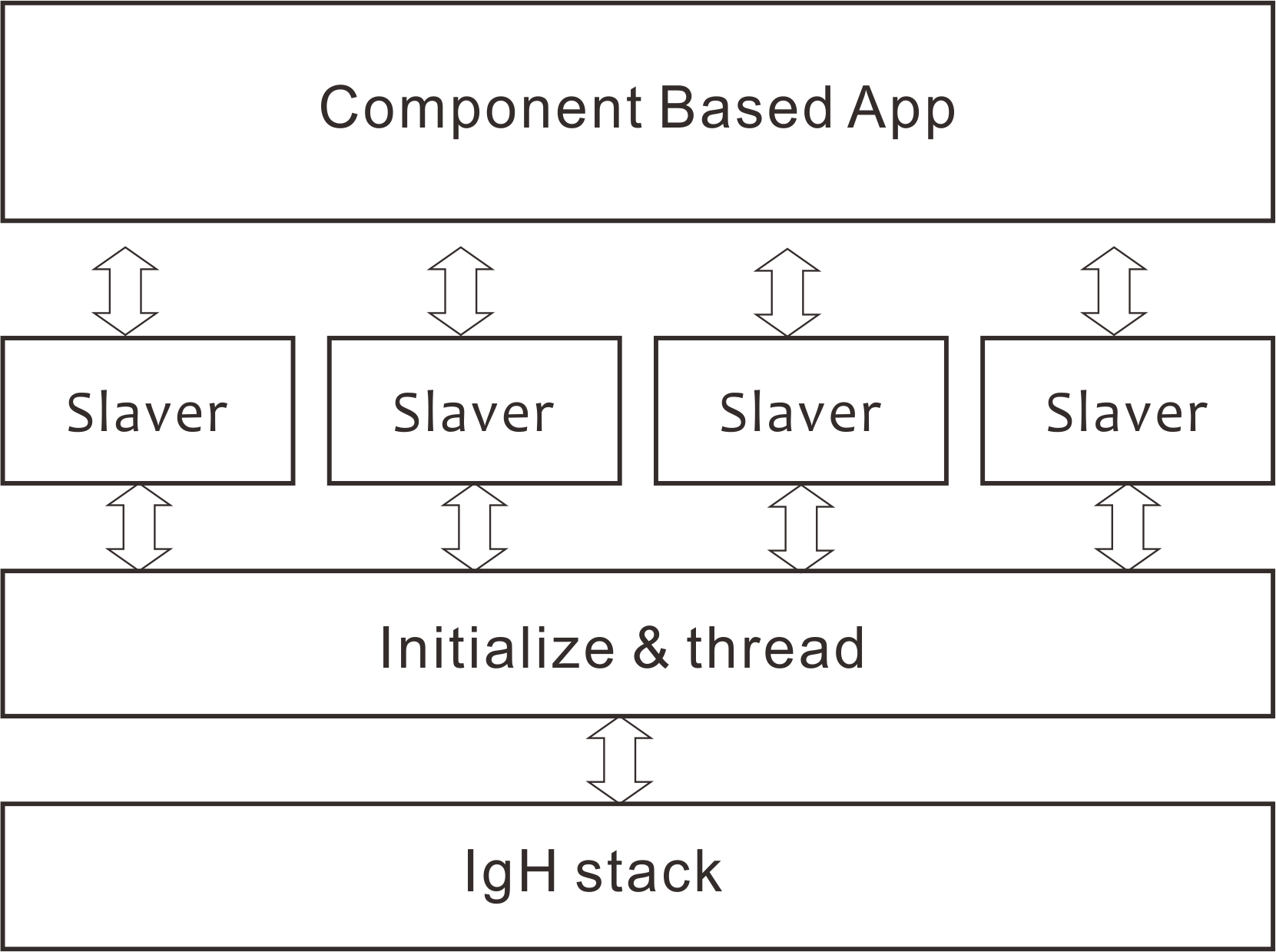
EtherCAT 伺服控制功能块实现
EtherCAT 是运动控制领域主要的通信协议,开源EtherCAT 主站协议栈 IgH 和SOEM 两个项目,IgH 相对更普及一些,但是它是基于Linux 内核的方式,比SOEM更复杂一些。使用IgH 协议栈编写一个应用程序,控制EtherCAT 伺服电机驱…...

如何基于OpenCV和Sklearn算法库开展机器学习算法研究
大家在做机器学习或深度学习研究过程中,不可避免都会涉及到对各种算法的研究使用,目前比较有名的机器学习算法库主要有OpenCV和Scikit-learn(简称Sklearn),二者都支持各种机器学习算法,主要有监督学习、无监…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
