「TCG 规范解读」TCG 主规范-设计原则
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alliance,TCPA)所开发的规范。现在的规范都不是最终稿,都还在不断的更新中,比如:TPM的规范就从原来的v1.0更新到v1.2,现在还在不断的修订。
主要规范在路线图中的位置

主要规范路线图
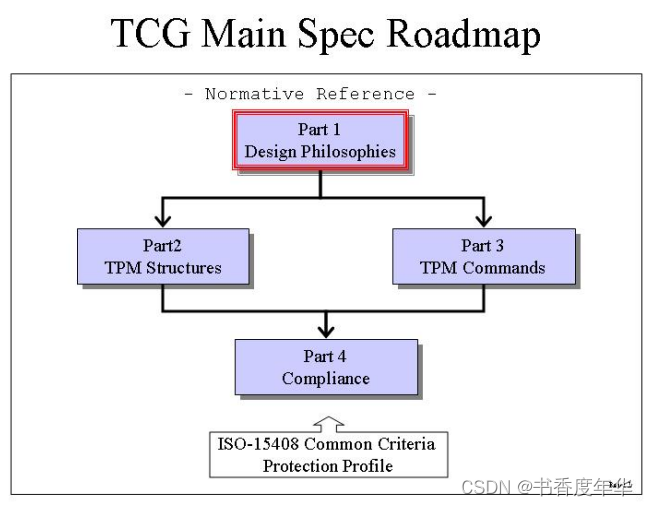
第一部分是主要规范的设计原则;
第二部分是 TPM 的结构;
第三部分是 TPM 的命令;
第四部分是由 ISO-15408 支持的合规;
设计原则
范围和读者
描述
保护
TPM 架构
背书密钥创建
证明实体密钥
TPM 属主关系<
相关文章:

「TCG 规范解读」TCG 主规范-设计原则
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alliance,TCPA)所开发的规范。现在的规范都不是最终稿,都…...
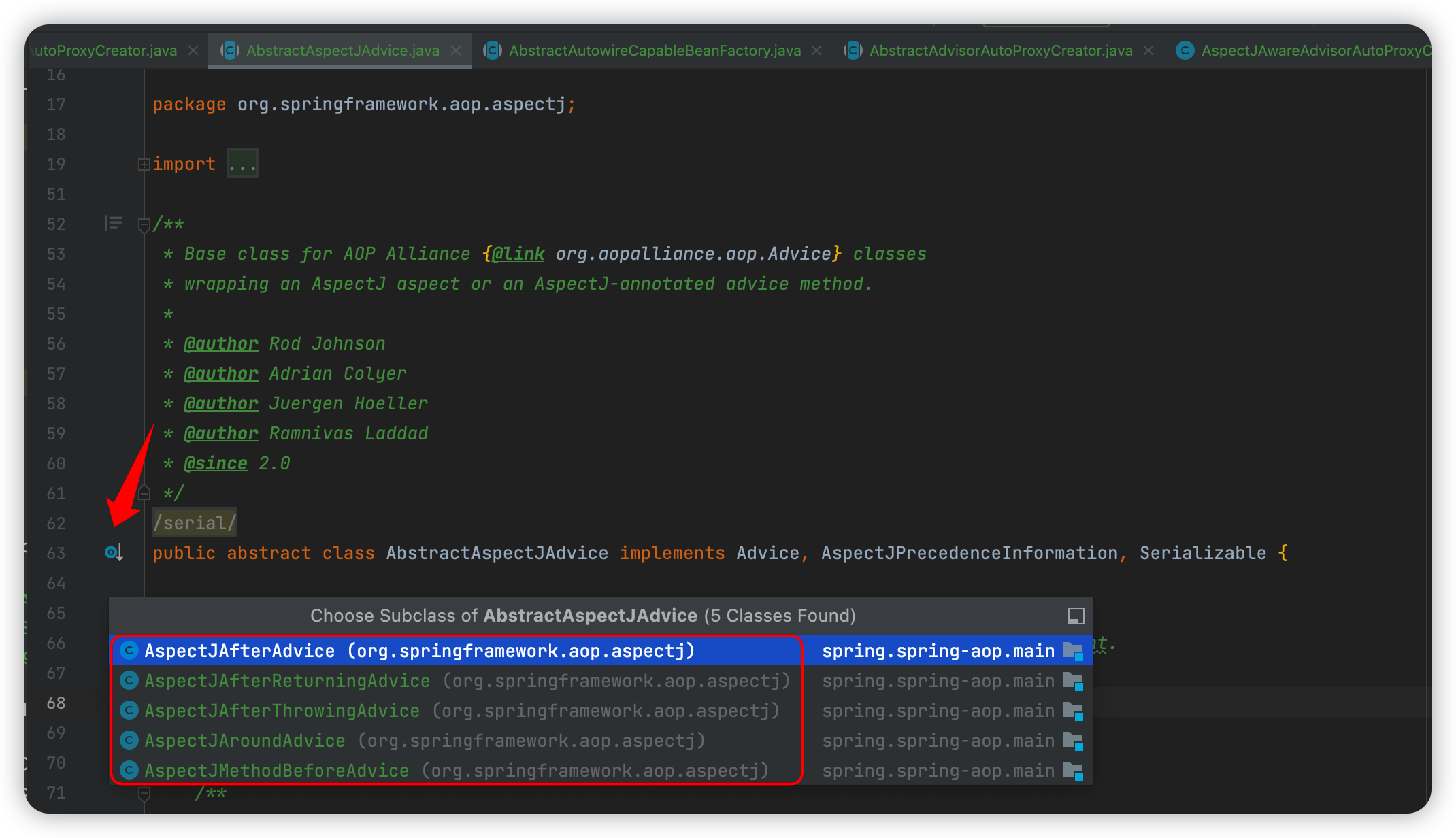
【Spring源码】Spring AOP的核心概念
废话版什么是AOP关于什么是AOP,这里还是要简单介绍下AOP,Aspect Oriented Programming,面向切面编程,通过预编译和运行期间提供动态代理的方式实现程序功能的统一维护,使用AOP可以降低各个部分的耦合度,提高…...

华为OD机试用Python实现 -【任务混部】(2023-Q1 新题)
华为OD机试题 华为OD机试300题大纲任务混部题目输入输出示例一输入输出说明示例二输入输出说明备注Code代码编写思路华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:blog.csdn.net/hihell/ca…...

Linux yum 命令
yum( Yellow dog Updater, Modified)是一个在 Fedora 和 RedHat 以及 SUSE 中的 Shell 前端软件包管理器。 基于 RPM 包管理,能够从指定的服务器自动下载 RPM 包并且安装,可以自动处理依赖性关系,并且一次安装所有依赖…...

package.json 字段配置
文章目录环境导入相关main 和 modulewebpack resolve.mainFieldsbrowserexports定义其他模块根据导入语句导出嵌套环境导出vue中 exports 用法自定义运行环境环境导入相关 main 和 module 根据导入模块时不同的模块规范语句查找不同的入口文件 "main": "dist…...

springboot中集成redis,二次封装成工具类
大家好,我是雄雄,欢迎关注微信公众号:** 雄雄的小课堂 ** 现在是:2023年2月28日11:01:56 前言 redis大家应该都不陌生,我们在好多场景下都会使用,最近在面试别人的时候,也会问一些关于redis的…...
Linux Vim 简介
文章目录01. 编辑器 Gedit 介绍02. 什么是 Vi(Vim)03. vim工作模式4.1 命令模式4.2 编辑模式4.3 末行模式04. vim教程05. vim基本操作06. vim实用操作7.1 命令模式下的操作7.2 末行模式下的操作01. 编辑器 Gedit 介绍 gedit 是一个 GNOME 桌面环境下兼容 UTF-8 的 文本编辑器。…...

软件测试面试题 —— 整理与解析(2)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:🌎【Austin_zhai】🌏 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能…...

HashMap与Hashtable的这九个区别,你知道吗
Hashtable Hashtable是原始的java.util的一部分,属于一代集合类,是一个Dictionary具体的实现 。Java1.2重构的Hashtable实现了Map接口,因此,Hashtable现在集成到了集合框架中。它和HashMap类很相似。 Hashtable与HashMap的区别 …...

Java奠基】掌握Java基础知识
目录 常见字面量 特殊字面量 数据类型 标识符 键盘录入 常见字面量 字面量就是数据在程序中的书写格式,字面量的分类如下: 字面量类型说明举例整数类型不带小数点的数字12,25小数类型带小数点的数字3.14,-5,20…...

Hive窗口函数-lead/lag函数
前面我们学习的first_value和last_value 取的是排序后的数据截止当前行的第一行数据和最后一行数据 Lag和Lead分析函数可以在一次查询中取出当前行后N行和前N行的数据,虽然可以不用排序,但是往往只有在排序的场景下取前面或者后面N 行数据才有意义 这种…...

2023JAVA面试题全集超全面超系统超实用!早做准备早上岸
2022年我凭借一份《Java面试核心知识点》成功拿下了阿里、字节、小米等大厂的offer,两年的时间,为了完成我给自己立的flag(拿下一线互联网企业offer大满贯),即使在职也一直在不断的学习与备战面试中!——或…...

FreeRTOS入门(05):事件组
文章目录目的基础说明相关函数使用演示总结目的 事件组是RTOS中相对常用的用于任务间交互的功能,这篇文章将对相关内容做个介绍。 本文代码测试环境见前面的文章:《FreeRTOS入门(01):基础说明与使用演示》 基础说明…...

【API网关】Kong安装和基本操作
文章目录前言一、API网关选型和Kong的安装1. 什么是API网关2. API网关技术选型3. 安装postgresql和migrations4. 安装kong5. 安装konga二、基本的路由转发配置1. kong的8001、8000和1337端口号的关系2. 基本的路由转发配置3. kong集成consul实现服务发现和负载均衡4. kong配置j…...

git --- stash用法
1 git stash命令介绍 // 保存当前分支的修改,回到上个版本的状态 git stash // 保存当前分支的修改,回到上个版本的状态,msg是保存当前修改的说明 git stash save "msg" // 用来展示所有保存的列表 git stash list // 用来展示某一保存记录所修改的操作 gi…...

【星海出品】VScode安装配置
安装VScode最好在官方网站上下载。 例如 https://code.visualstudio.com/Download 不知道自己的windows版本的话,可以命令行WINR 运行 输入: systeminfo | find "OS" //获取OS的版本信息。 systeminfo | find "系统类型" //获取系统…...

docker 基础命令备忘录
1. 官方安装docker curl -fsSL https://get.docker.com -o get-docker.sh && sh get-docker.shcurl -L "https://github.com/docker/compose/releases/download/v2.16.0/docker-compose-$(uname -s)-$(uname -m)" -o /usr/local/bin/docker-compose chmod x…...
)
华为OD机试 - 创建二叉树(Java JS Python)
题目描述 请按下列描述构建一颗二叉树,并返回该树的根节点: 1、先创建值为-1的根结点,根节点在第0层; 2、然后根据operations依次添加节点: operations[i] = [height, index] 表示对第 height 层的第index 个节点node, 添加值为 i 的子节点: 若node 无「左子节点」,则…...
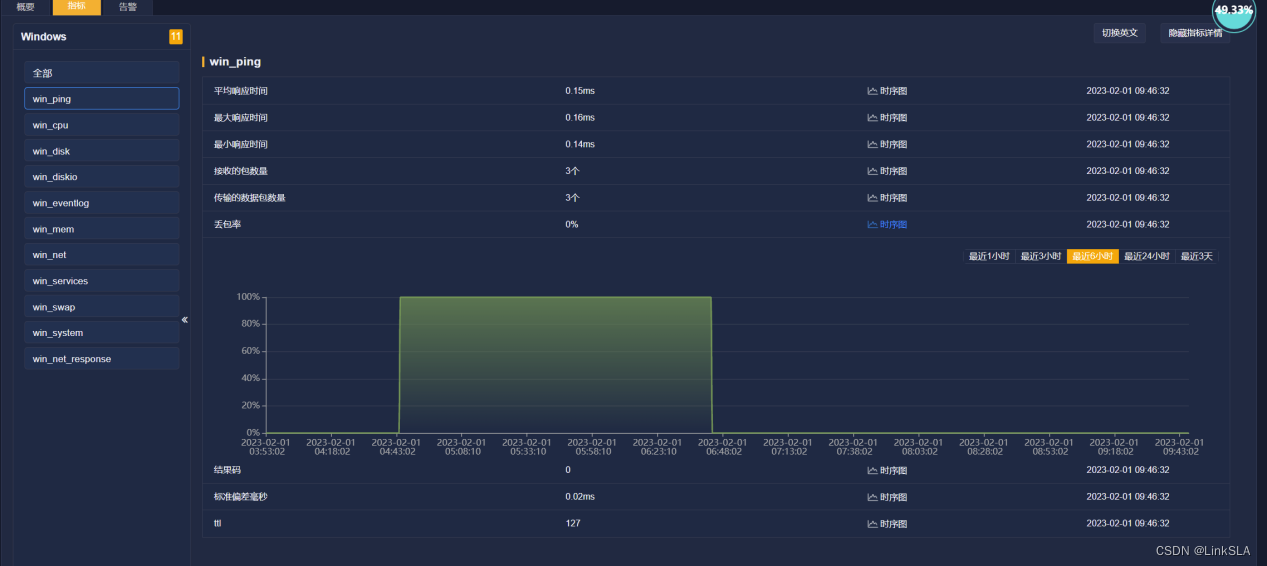
服务案例|基于IT事件管理,提升业务连续性
数字化经济时代,IT架构复杂性越来越高,业务连续性成为很多行业或企业最核心的任务。业务连续性管理是一个不断提升的过程,围绕事件“发现-响应-定位处理-降低发生”的事件处理思路,结合平台化运维,助力业务快速提升。 …...
你说下HashMap的工作原理?
我在网上看了很多文章 ,各种长篇大论 ,原理细节、实在看不下去了,所以着重讲一下,HashMap 面试会问到的点 说人话, 你们公司的集合 不会自研吧, 假如 你们叫 锤子科技 ,那老板也不会要求你去写一…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
