动态规划解决leetcode上的两道回文问题(针对思路)
本期主讲的是使用动态规划去解决两道回文问题,分别是
647. 回文子串 - 力扣(LeetCode)
516. 最长回文子序列 - 力扣(LeetCode)
而不是leetcode5.最长回文子串,虽然这道题也是回文问题,也可以使用dp来解决,但是这道题本人认为与647回文子串思路相同,但这里也给出大致的解题思路。
这道题求的是连续子数组问题,而且是最长的回文的子数组,虽然它只有一个字符串,但是我们也使用二维dp数组,一维代表起始子数组,另一维是标识该子数组的终点,然后从后往前遍历字符串,两层循环,分别指子串起始和末尾,然后判断当前两个下标对应字符是否相等,然后再看中间的子数组是否回文,若是则更新答案。
这道题的思路其实就是我们要讲的回文子串的思路,只不过处理数据有些不同而已,求最长子数组就是记录当前多长,和之前的比较。而这道记录的是有多少回文子串,实际思路是相同的
第一道题
先看代码:
class Solution {
public:int countSubstrings(string s) {int n=s.size();vector<vector<bool>>dp(n,vector<bool>(n,false));int res=0;for(int i=n-1;i>=0;--i){for(int j=i;j<n;++j){if(s[i]==s[j]){if(j-i<=1){dp[i][j]=true;++res;}else if(dp[i+1][j-1]){dp[i][j]=true;++res;}}}}return res;}
};我们以一个布尔类型二维数组做判断,循环就是刚才说的,从后往前,为什么从后往前,这是因为递推式的缘故,我们要判断当前字符相等的情况下,看一看该子串里面的内容是否回文,怎么看?它是比较i+1和j-1,所以一定要保证这一段已经被判断回文过了,所以我们才会选择从后往前遍历的方法,而内层循环你看着可能有些奇怪,但事实上它是正确的。因为如果两个下标对应相等还存在两种情况,一种是两下标指向同一字符,此时肯定回文,另一种是指向不同字符,但是这两个下标只差1,也就是说【a】和【aa】这两种情况的对应。我们都考虑了进来,当两下标相差大的时候,里面就会存有子数组我们才会进行判断,而此时判断的话,已经是之前遍历过的位置了,已经知道了它回不回文。
可能有读者会问,是否可以从字符串中间去进行向两边扩散的访问,以得到是否回文的情况,这一招很好用,对于判断整个字符串是否回文,以及判断整个字符串的最长回文子数组的长度,但是并不适用于本题,因为本题求解的是根据每一个下标的情况给出可能存在的所有回文的子数组的个数
而上面的那招中心探测,并不完全,如果使用中心探测至少要对每个子串都进行回文判断,所以无论如何你都逃脱不了,要判断每个子串的命运,而不是只在字符串的中心位置判断回文,而只On就能解决问题,你最少需要ON^2才可以解决问题。(至少我知道的方法里没有ON)
当然如果你是算法老鸟,你可以对二维数组进行一维的压缩,以解决减少时间复杂度的开销,但是通常我只会在简单的题解里才会想这种优化,稍稍复杂一点的题解,很容易出现各种问题,所以我一般倾向于解题,而不是给自己找麻烦。
第二道题
最长回文子序列,是不是看起来和那道最长回文子串差不多,这道题只不过是求不连续的子序列最长的长度。
但我们这里的思路并不沿用上面的思路。尽量不要使用回文子串那道题目的做法,会使得代码难写且含义不清晰,因为那道做法dp含义是针对于连续子数组的,我们很难只用true或false来判断中间字符串的回文长度到底为多少,而且在本题中,这样的bool数组并没有太多价值,因为如果要存子序列的最长数多半情况是用到其他变量辅助存储的,而bool数组起到的作用只是判断这段子数组是否回文,与这道题实际的问题有点相违背。
这道题我们采用如下的思路:
class Solution {
public:int longestPalindromeSubseq(string s) {int n=s.size();vector<vector<int>>dp(n,vector<int>(n,0));for(int i=0;i<n;++i)dp[i][i]=1;for(int i=n-1;i>=0;--i){for(int j=i+1;j<s.size();++j){if(s[i]==s[j])dp[i][j]=dp[i+1][j-1]+2;else dp[i][j]=max(dp[i][j-1],dp[i+1][j]);}}return dp[0][n-1];}
}; dp数组的含义代表当前ij范围内最长的回文子序列多长,子序列可以不连续
当此时ij对应下标字符相等,则用两下标中间的子串范围的最大回文子序列长度+2,也就是把s【i】和s【j】都加入进来
如果此时不相等,则判断如果只加进一个能否取得最长回文子序列,也就是说dp【i】【j-1】和dp【i+1】【j】它们两个比较然后取最大值。
为什么这样呢?因为s【i】和s【j】中间的子数组应该是以s【i+1】和s【j-1】为下标的,所以左边加进来s【i】就是dp【i】【j-1】右边加进来j就是dp【i+1】【j】
别忘了根据递推式的含义,最后返回的应该是dp【0】【s.size()-1】
代表从0开始到结束最长的回文子序列
是不是有疑问了?为什么这道题的内部循环变得更奇怪了?要使用j=i+1的初始化,这样不会越界吗?
接下来我们来解释一下这样做的原因。
里层循环i+1,并不是无用的,不能设置为j=i
有两个原因一个是浅显易见的,是因为两个下标指向同一字符的情况我们已经初始完毕了,另一原因是如果从j=i进来那第一次填数会导致数组非法下标访问,而第二次进来虽然推导时候也有些奇怪,因为i和j拉开距离过小的缘故,i会走到j的位置,也就是i上一次遍历的位置,j会走到i本次起始遍历位置,虽然奇怪,但是也是遍历过的,所以答案也是对的。
没错前面的循环是为了初始化,因为至少它的最长回文子序列一定是1,我们要把它初始化一下,这也方便接下来dp数组的正确填数。而由于递推式的缘故,我们也不能使内层循环写成j=i开始,要不然一开始就会越界,这道题不像上一道题,上一道题是极可能存在相邻两个相等的情况,而且那道题的dp数组含义也与本题不同。那道题j=i的初始化由于前面的if判断,j<=i的时候会有一个缓冲,不会过早进到中间子数组的判断,这道题递推式不行,它不具备那样的缓冲。
那我们可以加一个那样的判断吗?判断两字符相等且j<=I然后填数做缓冲不就可以了吗?
好问题,可以
但是求子序列的含义是我们可以允许不相邻的子序列也构成答案,也就是说子序列答案是包含了两个字符相邻回文,也就是子序列包含子数组的所有情况,没必要写一个特式专门用来判断这一步骤,这显得有点繁琐了,子序列的代码应该更适用于大多数的情况。
但如果加一步那样的判别可以使一开始的判断回文看起来正常一些,j也不用从i+1开始判断了,也是一种好的题解思路。
那这道题可以从字符串中间进行下标的开始匹配吗?我认为有点问题,类中心探测法无论是一次匹配还是每个字符的分别匹配,本质上都是用来解决连续的子数组的问题,用在子序列可能有点麻烦,我没有试过,感兴趣的读者可以自己试一下。我认为应该有点难度。
都看到这里了如果对您有用的话别忘了一键三连哦,如果是互粉回访我也会做的!
大家有什么想看的题解,或者想看的算法专栏、数据结构专栏,可以去看看往期的文章,有想看的新题目或者专栏也可以评论区写出来,讨论一番,本账号将持续更新。
期待您的关注
相关文章:
)
动态规划解决leetcode上的两道回文问题(针对思路)
本期主讲的是使用动态规划去解决两道回文问题,分别是 647. 回文子串 - 力扣(LeetCode) 516. 最长回文子序列 - 力扣(LeetCode) 而不是leetcode5.最长回文子串,虽然这道题也是回文问题,也可以…...

使用人工智能自动测试 Flutter 应用程序
移动应用程序开发的增长速度比以往任何时候都快。几乎每个企业都需要移动应用程序来保持市场竞争力。由于像 React Native 这样的跨平台移动应用程序开发框架允许公司使用单一源代码和单一编程语言构建 iOS 和 Android 应用程序, Flutter是 Google 支持的另一个热门…...
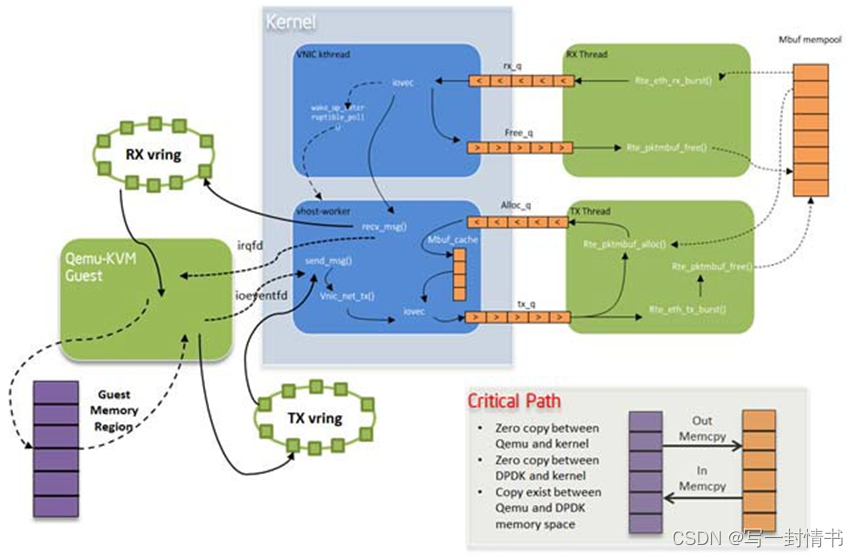
四、程序员指南:数据平面开发套件
REORDER LIBRARY 重排序库提供了根据其序列号对mbuf进行重排序的机制。 16.1 操作 重排序库本质上是一个对mbuf进行重新排序的缓冲区。用户将乱序的mbuf插入重排序缓冲区,并从中提取顺序正确的mbuf。 在任何给定时刻,重排序缓冲区包含其序列号位于序列…...

Go 之 captcha 生成图像验证码
目前 chptcha 好像只可以生成纯数字的图像验证码,不过对于普通简单应用来说也足够了。captcha默认将store封装到内部,未提供对外操作的接口,因此使用自己显式生成的store,可以通过store自定义要生成的验证码。 package mainimpor…...
【Java从入门到大牛】多线程
🔥 本文由 程序喵正在路上 原创,CSDN首发! 💖 系列专栏:Java从入门到大牛 🌠 首发时间:2023年11月18日 🦋 欢迎关注🖱点赞👍收藏🌟留言Ǵ…...
UE5 C++报错:is not currently enabled for Live Coding
解决办法: 再次打开项目,以此法打开:...
mysql服务器数据同步
在Linux和Windows之间实现MySQL服务器数据的同步。下面是一些常见的方法和工具: 复制(Replication):MySQL复制是一种常见的数据同步技术,可用于将一个MySQL服务器的数据复制到其他服务器。您可以设置主服务器ÿ…...

Docker Golang 开发环境搭建指南
Docker Golang 开发环境搭建指南 概述 在 Golang 开发中,搭建合适的开发环境是非常重要的。然而,由于 Golang 的跨平台特性,不同操作系统之间的配置差异可能会导致环境搭建过程变得复杂。为了简化这个过程并保持开发环境的一致性࿰…...
MFC保存窗口客户区为图片
首先的窗口输出一些内容; 菜单单击函数代码; void CgetmypicView::OnTestGetmypic() {// TODO: 在此添加命令处理程序代码HWND hwnd this->GetSafeHwnd();HDC hDC ::GetWindowDC(hwnd);//获取DC RECT rect;::GetClientRect(hwnd, &rect)…...
JAVA安全之Shrio550-721漏洞原理及复现
前言 关于shrio漏洞,网上有很多博文讲解,这些博文对漏洞的解释似乎有一套约定俗成的说辞,让人云里来云里去,都没有对漏洞产生的原因深入地去探究..... 本文从现象到本质,旨在解释清楚Shrio漏洞是怎么回事!…...
有Mac或无Mac电脑通用的获取安卓公钥的方案
从2023年9月开始,所有上架应用市场的app都需要进行APP备案。 其中后端服务器在阿里云的可以在阿里云备案,后端服务器在腾讯云的可以在腾讯云备案。但无论你是在什么云厂商里做备案,无一例外的是,无论是上架安卓应用还是上架IOS应…...
电池故障估计:Realistic fault detection of li-ion battery via dynamical deep learning
昇科能源、清华大学欧阳明高院士团队等的最新研究成果《动态深度学习实现锂离子电池异常检测》,用已经处理的整车充电段数据,分析车辆当前或近期是否存在故障。 思想步骤: 用正常电池的充电片段数据构造训练集,用如下的方式构造…...
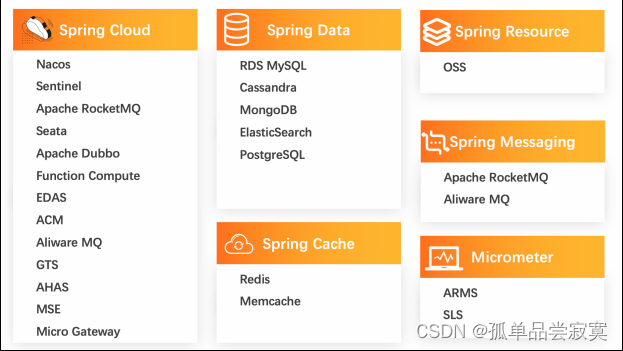
微服务和Spring Cloud Alibaba介绍
1、微服务介绍 1.1 系统架构演变 随着互联网的发展,网站应用的规模也在不断的扩大,进而导致系统架构也在不断的进行变化。从互联网早起到现在,系统架构大体经历了下面几个过程: 单体应用架构 —> 垂直应用架构 —> 分布 式架构—>…...

【js】 lodash命名转换和封装
▒ 目录 ▒ 🛫 导读需求开发环境 1️⃣ lodash转换函数h3与underscore比较 2️⃣ 实战:对象属性名转换函数封装单元测试 🛬 文章小结📖 参考资料 🛫 导读 需求 爬虫中经常出现各种类型的命名,往往一个对象…...

RK3568驱动指南|第七篇 设备树-第67章 of操作函数实验:获取属性
瑞芯微RK3568芯片是一款定位中高端的通用型SOC,采用22nm制程工艺,搭载一颗四核Cortex-A55处理器和Mali G52 2EE 图形处理器。RK3568 支持4K 解码和 1080P 编码,支持SATA/PCIE/USB3.0 外围接口。RK3568内置独立NPU,可用于轻量级人工…...
vue3安装vue-router
环境 node 18.14.2 yarn 1.22.19 windows 11 vite快速创建vue项目 参考 安装vue-touter 官网 yarn add vue-router4src下新建router文件夹,该文件夹下新建index.ts // router/index.ts 文件 import { createRouter, createWebHashHistory, RouterOptions, Ro…...
〖大前端 - 基础入门三大核心之JS篇㊱〗- JavaScript 的DOM节点操作
说明:该文属于 大前端全栈架构白宝书专栏,目前阶段免费,如需要项目实战或者是体系化资源,文末名片加V!作者:不渴望力量的哈士奇(哈哥),十余年工作经验, 从事过全栈研发、产品经理等工作…...

【计算机基础】优雅的PPT就应该这样设计
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

Vatee万腾的科技征程:Vatee数字化创新的前沿探讨
在Vatee万腾的科技征程中,我们目睹了一场数字化创新的引领之旅,探讨了Vatee在科技前沿的独到见解。Vatee万腾不仅仅是一家科技公司,更是一支前行不辍的冒险队伍,通过不断突破自我,探索未知领域,引领着数字化…...
【PB续命05】WinHttp.WinHttpRequest的介绍与使用
0 WinHttp.WinHttpRequest简介 winhttp.winhttprequest是Windows操作系统中的一个API函数,用于创建和发送HTTP请求。它可以用于从Web服务器获取数据,或将数据发送到Web服务器。该函数提供了许多选项,例如设置请求头、设置代理服务器、设置超…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
