机器学习算法——集成学习
目录
- 1. Bagging
1. Bagging
Bagging(bootstrap aggregating:自举汇聚法)也叫装袋法,其思想是通过将许多相互独立的学习器的结果进行结合,从而提高整体学习器的泛化能力,是一种并行集成学习方法。
工作流程
- 从原始样本集中使用Bootstraping(有放回抽样,这种抽样方法产生的样本子集能很好的反映总体的分布特性)方法抽取n个训练样本,共进行K轮抽取,得到K个训练集(训练集之间相互独立)。
- 对于每个训练集,使用相同的数据学习算法(比如决策树、KNN等)独立训练一个基本模型。
- 将测试样例输入到所有基本模型中,每个模型都给出一个预测值。对于分类问题:通过投票的方式确定分类结果(每个模型只有一票);对于回归问题:计算预测值的均值作为预测结果。
代码实践(Jupyter Notebook实现)
from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt#------------------------------------------------------------------#
# 使用datasets模块导入鸢尾花数据集,并切分特征值和标签值
# train_test_split(x_data, y_data):将数据集划分为测试集和训练集,
# 默认情况下,训练集占3/4,测试集占1/4
#-----------------------------------------------------------------#
iris = datasets.load_iris()
x_data = iris.data[:,:2]
y_data = iris.target
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data)
# 利用等高线绘制分类边界图
def plot(model):# 获取数据值所在的范围x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵元素xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))#-----------------------------------------------------## 预测分类结果# ravel():将多为数据展平为一维数据# np.c_:按列连接两个数组,即拼接成点的坐标的形式# contourf(xx, yy, z):创建填充等高线图,参数需为二维数组#-----------------------------------------------------#z = model.predict(np.c_[xx.ravel(), yy.ravel()])z = z.reshape(xx.shape)cs = plt.contourf(xx, yy, z)
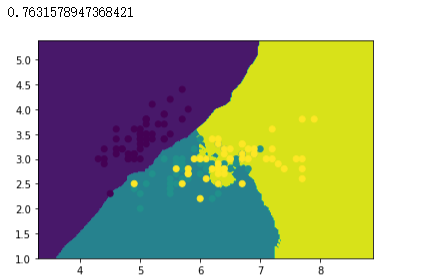
# 创建KNN模型,使用训练集训练模型
knn = neighbors.KNeighborsClassifier()
knn.fit(x_train, y_train)
# 绘制分类边界图
plot(knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
knn.score(x_test, y_test)
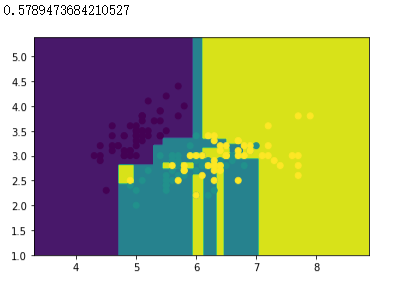
# 创建CART决策树模型,使用训练集训练模型
dtree = tree.DecisionTreeClassifier()
dtree.fit(x_train, y_train)
# 绘制分类边界图
plot(dtree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
dtree.score(x_test, y_test)
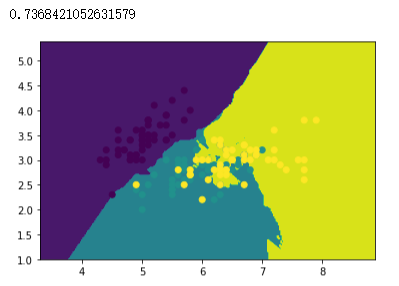
# 创建 Bagging 分类器对象,以KNN分类器作为基分类器,创建100个KNN基分类器
bagging_knn = BaggingClassifier(knn, n_estimators=100)
# 模型拟合
bagging_knn.fit(x_train, y_train)
# 绘制分类边界图
plot(bagging_knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
bagging_knn.score(x_test, y_test)
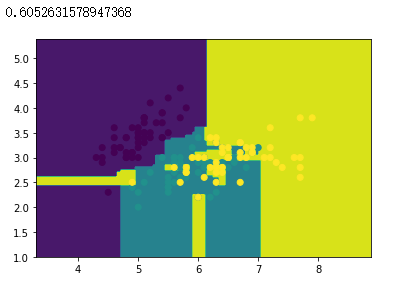
# 创建 Bagging 分类器对象,以CART决策树分类器作为基分类器,创建100个基分类器
bagging_tree = BaggingClassifier(dtree, n_estimators=100)
# 模型拟合
bagging_tree.fit(x_train, y_train)
# 绘制分类边界图
plot(bagging_tree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
bagging_tree.score(x_test, y_test)
准确率汇总
| 算法 | 准确率 |
|---|---|
| KNN | 73.6 8% |
| Bagging(KNN) | 76.32% |
| DecisionTree | 57.89% |
| Bagging(DecisionTree) | 60.53% |
注:由于数据集切分的随机性和Bagging中每个基分类器所使用的训练集不同,因此每次运行的结果可能不同,且Bagging的准确率可能会比单分类器的准确率低。
相关文章:

机器学习算法——集成学习
目录 1. Bagging 1. Bagging Bagging(bootstrap aggregating:自举汇聚法)也叫装袋法,其思想是通过将许多相互独立的学习器的结果进行结合,从而提高整体学习器的泛化能力,是一种并行集成学习方法。 工作流…...
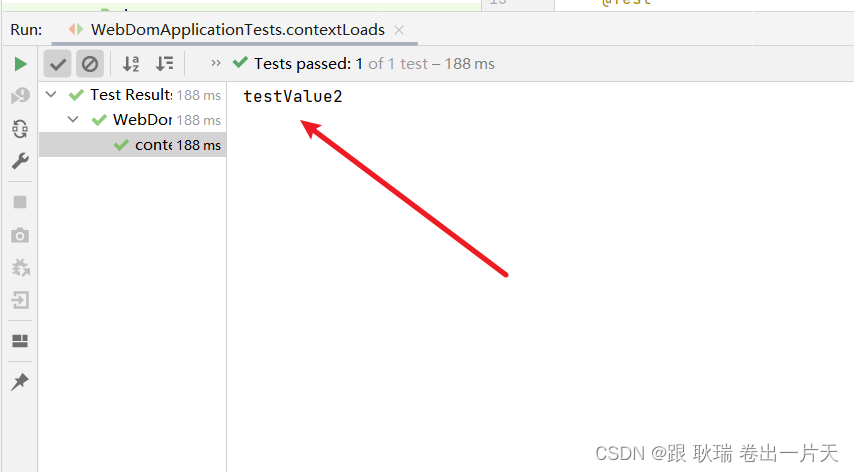
java springboot在当前测试类中添加临时属性 不影响application和其他范围
目前 我们的属性基本都写在 application.yml 里面了 但是 如果 我们只是想做一下临时变量的测试 有没有办法实现呢? 显然是有的 这里 我们还是先在application.yml中去写一个 test属性 下面加个prop 然后 我们尝试在测试类中 获取一下这个属性 直接用 Value 读取…...

原型网络Prototypical Network的python代码逐行解释,新手小白也可学会!!由于工作量大,准备整8个系列完事,-----系列5
文章目录 前言一、原始程序---计算原型,开始训练,计算损失二、每一行代码的详细解释2.1 粗略分析2.2 每一行代码详细分析 前言 承接系列4,此部分属于原型类中的计算原型,开始训练,计算损失函数。 一、原始程序—计算原…...

milvus数据库的数据管理-插入数据
一、插入数据 1.准备数据 数据必须与数据库中定义的字段元数据一致,与集合的模式匹配 import random data [[i for i in range(2000)],[str(i) for i in range(2000)],[i for i in range(10000, 12000)],[[random.random() for _ in range(2)] for _ in range(2…...
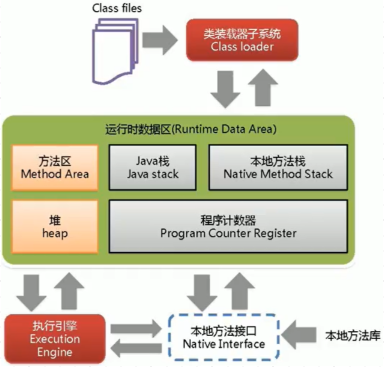
系列一、请谈谈你对JVM的理解?Java8的虚拟机有什么更新?
一、请谈谈你对JVM的理解?Java8的虚拟机有什么更新? JVM是Java虚拟机的意思。它是建立在操作系统之上的,由类加载器子系统、本地方法栈、Java栈、程序计数器、方法区、堆、本地方法库、本地方法接口、执行引擎组成。 (1࿰…...

恕我直言,大模型对齐可能无法解决安全问题,我们都被表象误导了
是否听说过“伪对齐”这一概念? 在大型语言模型(LLM)的评估中,研究者发现了一个引人注目的现象:当面对多项选择题和开放式问题时,模型的表现存在显著差异。这一差异根源在于模型对复杂概念的理解不够全面&…...

Apache Airflow (九) :Airflow Operators及案例之BashOperator及调度Shell命令及脚本
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹…...
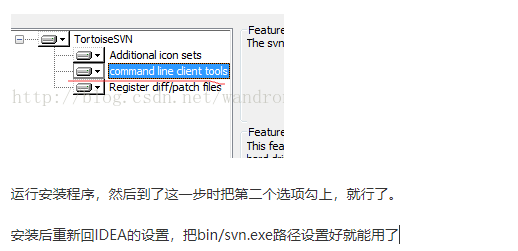
IJ中配置TortoiseSVN插件:
文章目录 一、报错情况:二、配置TortoiseSVN插件: 一、报错情况: 由于公司电脑加密,TortoiseSVN菜单没有提交和更新按钮,所以需要使用IJ的SVN进行代码相关操作 二、配置TortoiseSVN插件: 需要设置一个svn.…...

个人实现在线支付,一种另类的在线支付解决方案
Hi, I’m Shendi 个人实现在线支付,一种另类的在线支付解决方案 个人实现在线支付的方式 对于在线支付,最多的是接入微信与支付宝。但都需要营业执照,不适用于个人。 当然,可以去办理一个个体工商户,但对我这种小额收…...

浅谈智能安全配电装置应用在银行配电系统中
【摘要】银行是国家重点安全保护部分,关系到社会资金的稳定,也是消防重点单位。消防安全是银行工作的重要组成部分。在银行配电系统中应用智能安全配电装置,可以提高银行的智能控制水平,有效预防电气火灾。 【关键词】银行&#…...
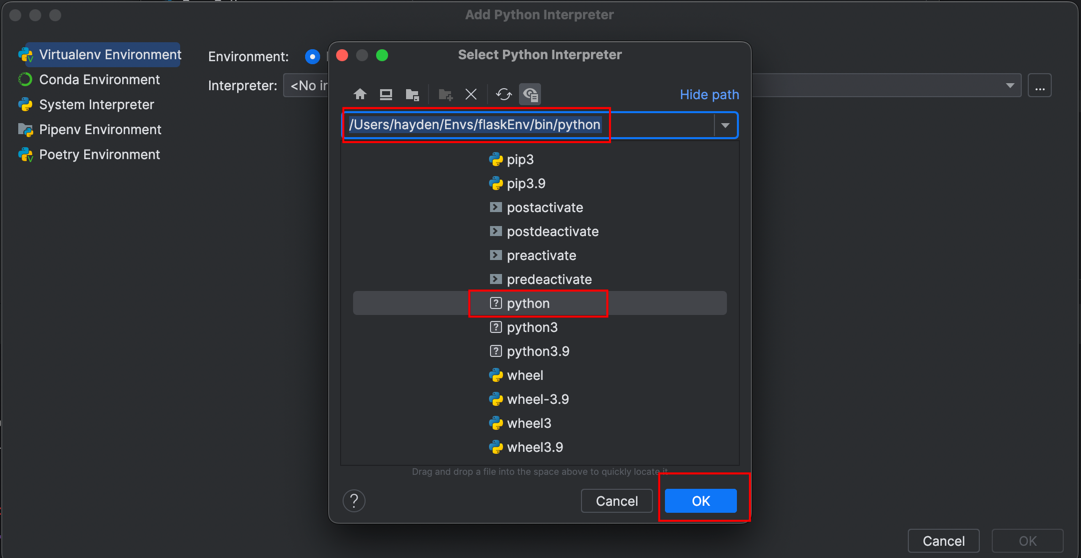
macOS下如何使用Flask进行开发
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是全栈工…...
记一次服务器配置文件获取OSS
一、漏洞原因 由于网站登录口未做双因子校验,导致可以通过暴力破解获取管理员账号,成功进入系统;未对上传的格式和内容进行校验,可以任意文件上传获取服务器权限;由于服务器上配置信息,可以进一步获取数据库权限和OSS管理权限。二、漏洞成果 弱口令获取网站的管理员权限通…...

合众汽车选用风河Wind River Linux系统
导读合众新能源汽车股份有限公司近日选择了Wind River Linux 用于开发合众智能安全汽车平台。 合众智能安全汽车平台(Hozon Automo-tive Intelligent Security Vehicle Plat-form)是一个面向高性能服务网关及车辆控制调度的硬件与软件框架,将于2024年中开始投入量产…...
)
PTA平台-2023年软件设计综合实践_5(指针及引用)
第一题 6-1 调和平均 - C/C 指针及引用 函数hmean()用于计算整数x和y的调和平均数,结果应保存在指针r所指向的浮点数对象中。当xy等于0时,函数返回0表示无法计算,否则返回1。数学上,两个数x和y的调和平均数 z 2xy/(xy) 。 直接…...

智慧卫生间
智慧卫生间 获取ApiKey/SecretKey获取Access_token获取卫生间实时数据返回说明 获取ApiKey/SecretKey ApiKey/SecretKey采用 线下获取的方式,手动分配。 获取Access_token 向授权服务地址http://xxxxxx:12345/token(示意)发送post请求,并在data中带上…...
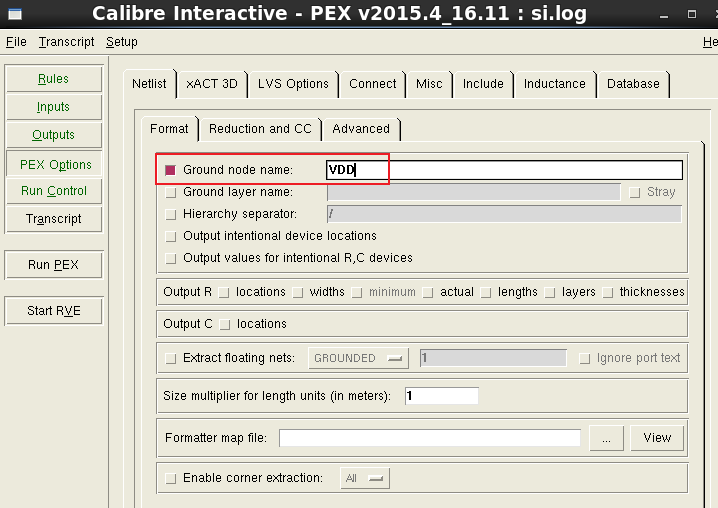
Cadence virtuoso drc lvs pex 无法输入
问题描述:在PEX中的PEX options中 Ground node name 无法输入内容。 在save runset的时候也出现无法输入名称的情况 解决办法: copy一个.bashrc文件到自己的工作目录下 打开.bashrc文件 在.bashrc中加一行代码:unset XMODIFIERS 在终端sour…...
, 分析调用链, 编写POC)
反序列化漏洞(2), 分析调用链, 编写POC
反序列化漏洞(2), 反序列化调用链分析 一, 编写php漏洞脚本 http://192.168.112.200/security/unserial/ustest.php <?php class Tiger{public $string;protected $var;public function __toString(){return $this->string;}public function boss($value){eval($valu…...

Pytorch reshape用法
这里-1是指未设定行数,程序自动计算,所以这里-1表示任一正整数 example reshape(-1, 1) 表示(任意行,1列),4行4列变为16行1列reshape(1, -1) 表示(1行,任意列)…...

Latex 辅助写作工具
语法修改 https://app.grammarly.com/润色 文心一言、ChatGPTlatex 编辑公式 https://www.latexlive.comlatex 编辑表格 https://www.tablesgenerator.comlatex 图片转公式 https://www.tablesgenerator.com...

frp新版本frp_0.52.3设置
服务端 frps.toml cp /root/frp/frpc /usr/bin #bindPort 7000 bindPort 7000# 如果指定了“oidc”,将使用 OIDC 设置颁发 OIDC(开放 ID 连接)令牌。默认情况下,此值为“令牌”。auth.method “token” auth.method "…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
