【算法每日一练]-图论(保姆级教程 篇5(LCA,最短路,分层图)) #LCA #最短路计数 #社交网络 #飞行路线 # 第二短路
今天讲最短路统计和分层图
目录
题目:LCA
思路:
题目:最短路计数
思路:
题目:社交网络
思路:
题目:飞行路线
思路:
题目:第二短路
思路:
题目:LCA


思路:
非常明显了,之前就说过倍增迭代就是一个一个选区间使总长度达到 M(凑一个数),用不大于它最大的二的次幂,减去之后,再重复这个过程。所以LCA+倍增逼近是最快的。
#include<bits/stdc++.h> //最近公共祖先LCA P3379:给一棵数,求任意两点的LCA
using namespace std;
const int maxn=500002;
int n,m,s,tot=0;
int head[maxn],d[maxn],p[maxn][21];//d存的是深度(deep),p[i][j]存的从i向上走2的j次方那么长的路径到的父节点
struct node{int v,next;}e[maxn*2];//存数要开两倍
void add(int u,int v){e[++tot]={v,head[u]};head[u]=tot;} void dfs(int u,int fa)// 首先进行的预处理,将所有点的deep和p的初始值dfs出来
{d[u]=d[fa]+1; p[u][0]=fa; //处理深度,父节点for(int i=1;(1<<i)<=d[u];i++)//i<log(d[u]) 处理每个u的st表p[u][i]=p[p[u][i-1]][i-1];for(int i=head[u];i;i=e[i].next){ //处理u的孩子的st表int v=e[i].v;if(v!=fa) dfs(v,u);//只能向下走,不能向上走}
}
int lca(int a,int b) //非常标准的lca查找(两次逼近)
{if(d[a]>d[b]) swap(a,b); //保证a是在b结点上方(d[b]大)for(int i=20;i>=0;i--){if(d[a]<=d[b]-(1<<i)) b=p[b][i];//向上逼近(b向上移到和a同一个深度)} if(a==b) return a; //特判for(int i=20;i>=0;i--){if(p[a][i]==p[b][i]) continue; //向上逼近(A和B一起向上,不断逼近最下端的公共祖先)else a=p[a][i],b=p[b][i]; }return p[a][0]; //找出最后a值的数字
}
int main()
{int a,b;scanf("%d%d%d",&n,&m,&s);//n个结点,m次询问,s是树根编号for(int i=1;i<n;i++){scanf("%d%d",&a,&b);add(a,b); add(b,a); //无向图,要加两次 }dfs(s,0);for(int i=1;i<=m;i++){scanf("%d%d",&a,&b);printf("%d\n",lca(a,b));}return 0;
}
题目:最短路计数


思路:
注意到每条路径的权值都是1,难怪结果会那么大。
dikjkstra和spfa版本最短路计数:
1,维护最短路时产生的:那就是映射关系(因为引入的是周围点,相当于ans[v]=ans[cur]*1)
2,新最短路:发现了新的最短路就相加
floyd版本最短路计数:
1,维护最短路时产生的:(因为引入的是任意点,故ans[i][j]=ans[i][k]*ans[k][j])
2,新最短路:发现了新的最短路就相加、
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=1e6+5,M=2e6+5;
int mod=100003,n,m,tot=0;
int head[N],vis[N],dis[N],ans[N];
priority_queue<pii,vector<pii>,greater<pii>>Q;
struct node {int to;int next;}e[M*2];
void add(int u,int v){e[++tot]=(node){v,head[u]};head[u]=tot;}
void dijkstra(int s){memset(dis,0x3f,sizeof(dis));Q.push({0,s});dis[s]=0;ans[s]=1;while(!Q.empty()){int cur=Q.top().second;Q.pop();if(vis[cur])continue;//跳不跳无所谓,无非耗点时间vis[cur]=1;for(int i=head[cur];i;i=e[i].next){int v=e[i].to;if(dis[cur]+1<dis[v])dis[v]=dis[cur]+1,ans[v]=ans[cur],Q.push({dis[v],v});//映射最短路(路过此点可以变短,那么最短路就和它有关)else if(dis[cur]+1==dis[v])ans[v]+=ans[cur],ans[v]%=mod;//新最短路(发现了另外的最短路就相加)}}
}
int main(){cin>>n>>m;int x,y;for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);add(x,y);add(y,x);}dijkstra(1);//spfa(1);for(int i=1;i<=n;i++){cout<<ans[i]<<'\n';}
}
//spfa版本:这个版本更快!!!!
void spfa(int s){memset(dis,0x3f,sizeof(dis));queue<int>q;vis[s]=1;q.push(s);dis[s]=0;ans[s]=1;while(!q.empty()){int cur=q.front();q.pop();vis[cur]=0;for(int i=head[cur];i;i=e[i].next){int v=e[i].to;if(dis[cur]+1<dis[v]){dis[v]=dis[cur]+1;ans[v]=ans[cur];if(!vis[v])q.push(v),vis[v]=1; }else if(dis[cur]+1==dis[v])ans[v]+=ans[cur],ans[v]%=mod;}}
}
题目:社交网络



思路:
点i的重要程度=∑从s到t的且经过i最短路条数/从s到t的最短路条数(s!=i,t!=i)
主要还是floyd算法,求出每个(i,j)对每个k的重要程度为ans[k]
求到某点时最短路径数:
1,只要最短路更新,那么最短路个数也要更新
2,如果发现了新的最短路,那么就相加
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=110;
ll INF,dis[N][N],e[N][N];//e[i][j]表示(i,j)的最短路径数
double ans[N];//每个点的重要程度
int main(){int n,m;ll x,y,z;cin>>n>>m;memset(dis,0x7f,sizeof(dis));INF=dis[1][1];//初始化INF无穷大for(int i=1;i<=m;i++){scanf("%lld%lld%lld",&x,&y,&z);dis[x][y]=dis[y][x]=z;e[x][y]=e[y][x]=1;//初始化e[i][j]}for(int i=1;i<=n;i++) dis[i][i]=0;//对角线为0,但是不写也对其余任何边都没有影响,写不写随你for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){if(dis[i][k]==INF||dis[k][j]==INF)continue;//有不通的就直接跳过if(dis[i][j]>dis[i][k]+dis[k][j]){dis[i][j]=dis[i][k]+dis[k][j];//每个边只会更新一次,即当前最优e[i][j]=e[i][k]*e[k][j];//只要最短路更新,则最短路对应的个数也要更新即可continue;}if(dis[i][j]==dis[i][k]+dis[k][j]){//找到了第二条最短路,就相加e[i][j]+=e[i][k]*e[k][j];}}for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){if(i==j||j==k||i==k)continue;if(dis[i][j]==dis[i][k]+dis[k][j])//对k遍历每个(i,j)ans[k]+=(1.0*e[i][k]*e[k][j])/e[i][j];}for(int i=1;i<=n;i++)printf("%0.3f\n",ans[i]);
}
题目:飞行路线


思路:
一个图中任意两个点都可以权值变成0,最多有k次,我们常常建立k层的分层图,相邻层所有点建立权值为0的立体边,然后跑最短路即可
#include <bits/stdc++.h>
using namespace std;
int cnt,head[110005];
int dis[110005];
bool vis[110005]; //标记当前白点,如果不想用vis,也可以判断取出元素的dis和dis数组中值是否一样
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>> > Q; //堆优化(first是值,second是下标)
struct Edge{ int to,w,next;}e[2500001];
void add(int u,int v,int w) { e[++cnt]=(Edge){v,w,head[u]}; head[u]=cnt;}
void Dijkstra(int s)//dijktra+堆优化
{memset(dis,0x3f,sizeof(dis));dis[s]=0;Q.push(make_pair(0,s));while(!Q.empty()) //必须用empty, size是求大小的,会慢一些 !!!{int u=Q.top().second; Q.pop();if(vis[u]) continue; //已经是白点的就跳过vis[u]=1; //标记成白点for(int i=head[u];i;i=e[i].next){int v=e[i].to,w=e[i].w;if(dis[v]>dis[u]+w) dis[v]=dis[u]+w,Q.push(make_pair(dis[v],v));}}
}int main()
{int n,m,k,s,t;cin>>n>>m>>k>>s>>t; //城市数,航线数,免费次数,起始城市号,终点城市号int u,v,c;for(int i=0;i<m;++i){cin>>u>>v>>c;//两个城市航线,费用for(int j=0;j<=k;++j){//建立每层图add(u+j*n,v+j*n,c);add(v+j*n,u+j*n,c);if(j!=k){//第k层下面没有了,就别建了add(u+j*n,v+(j+1)*n,0); //分层图:所有相邻层间:上下层u,v的权值为0add(v+j*n,u+(j+1)*n,0);}}}for(int i=1;i<=k;++i){add(t+(i-1)*n,t+i*n,0);}//处理奇葩数据Dijkstra(s);printf("%d",dis[t+k*n]);return 0;
}
题目:第二短路
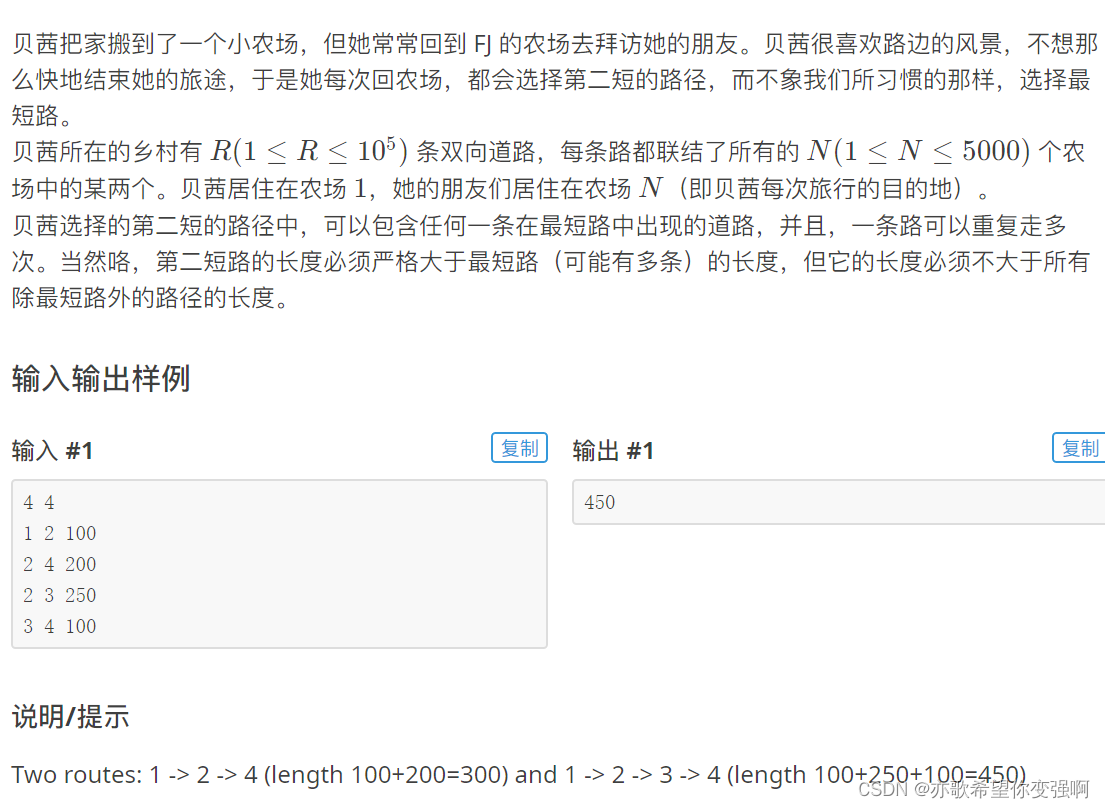
思路:
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=5005,M=100005;
int n,m,tot,flag;
int head[N],d1[N],d2[N],vis[N];
priority_queue<pii,vector<pii>,greater<pii> > Q;
struct node{int to;int w;int next;}e[M*2];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}
void dijkstra(int s){memset(d1,0x3f,sizeof(d1));//d1存放第一短路memset(d2,0x3f,sizeof(d2));//d2存放第二短路Q.push(make_pair(0,s));d1[s]=0;while(!Q.empty()){int cur=Q.top().second;Q.pop();if(vis[cur])continue;//vis数组可有可无,即便旧白点引入也掀不起变化,无非多走了几步vis[cur]=1;for(int i=head[cur];i;i=e[i].next){int v=e[i].to,w=e[i].w;flag=0;if(d1[cur]+w<d1[v])d2[v]=d1[v],d1[v]=d1[cur]+w,flag=1;//维护最短路,更新前的最短路就是次短路if(d1[cur]+w>d1[v]&&d1[cur]+w<d2[v])d2[v]=d1[cur]+w,flag=1;//最短路没有变化,更新次短路if(d2[cur]+w<d2[v])d2[v]=d2[cur]+w,flag=1;//维护次短路,如果d2[s]初始化成0,那么这个地方就出问题了if(flag)Q.push(make_pair(d1[v],v));}}
}
int main(){cin>>n>>m;int u,v,w;for(int i=1;i<=m;i++){scanf("%d%d%d",&u,&v,&w);add(u,v,w);add(v,u,w);}dijkstra(1);cout<<d2[n];
}相关文章:

【算法每日一练]-图论(保姆级教程 篇5(LCA,最短路,分层图)) #LCA #最短路计数 #社交网络 #飞行路线 # 第二短路
今天讲最短路统计和分层图 目录 题目:LCA 思路: 题目:最短路计数 思路: 题目:社交网络 思路: 题目:飞行路线 思路: 题目:第二短路 思路: 题目&a…...
德迅云安全为您介绍关于抗D盾的一些事
抗D盾概述: 抗D盾是新一代的智能分布式云接入系统,接入节点采用多机房集群部署模式,隐藏真实服务器IP,类似于网站CDN的节点接入,但是“抗D盾”是比CDN应用范围更广的接入方式,适合任何TCP 端类应用包括&am…...
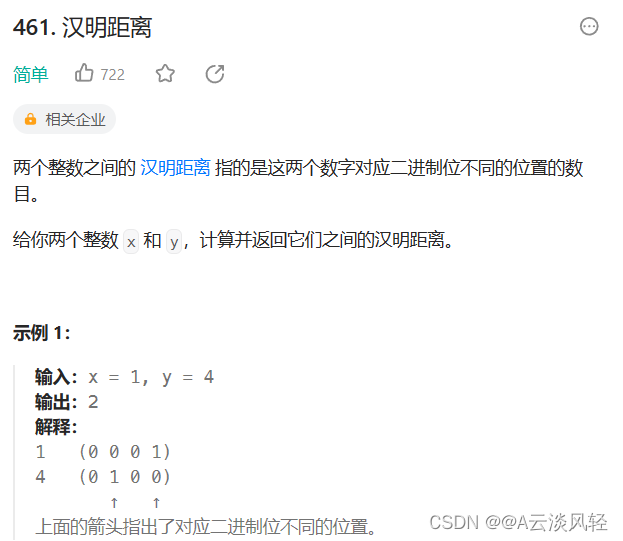
leetcode算法之位运算
目录 1.判断字符是否唯一2.丢失的数字3.两整数之和4.只出现一次的数字II5.消失的两个数字6.位1的个数7.比特位计数8.汉明距离 1.判断字符是否唯一 判断字符是否唯一 class Solution { public:bool isUnique(string astr) {//利用鸽巢原理做优化if(astr.size()>26) return…...
java常用的几个图片处理工具对Tiff文件的支持
ImageMagick 官网 https://imagemagick.org/, 支持多种格式。命令行工具很适合调试。功能很强大. 还有一款工具GraphicsMagick 是从ImageMagick的基础上研发出来的。 OpenCV 官网 https://opencv.org/ , github地址https://github.com/opencv/opencv&…...
-SQL查询篇(11)-联结表)
SQL必知会(二)-SQL查询篇(11)-联结表
第12课、联结表 联结表 使用联结:之前的 SELECT 查询某些列,只是针对一张表进行检索的。(即 FROM 表名)。但是如果用户想要使用 SELECT 对存储在不同表中的某些列时,则需要使用联结表的方式来实现。 例子中有建立两个…...

多模态大一统:开启全模态LLM和通用AI时代的大门
多模态大一统:开启全模态LLM和通用AI时代的大门 1. 目前多模态实现的方法1.1 单独训练各领域模型1.2 多任务学习1.3 集成多模态模型1.4 通用多模态模型2. 多模态统一难点2.1 数据集对齐和融合2.2 大规模计算资源需求2.3 各领域特性的兼容性2.4 可解释性和泛化能力3. 全模态的好…...
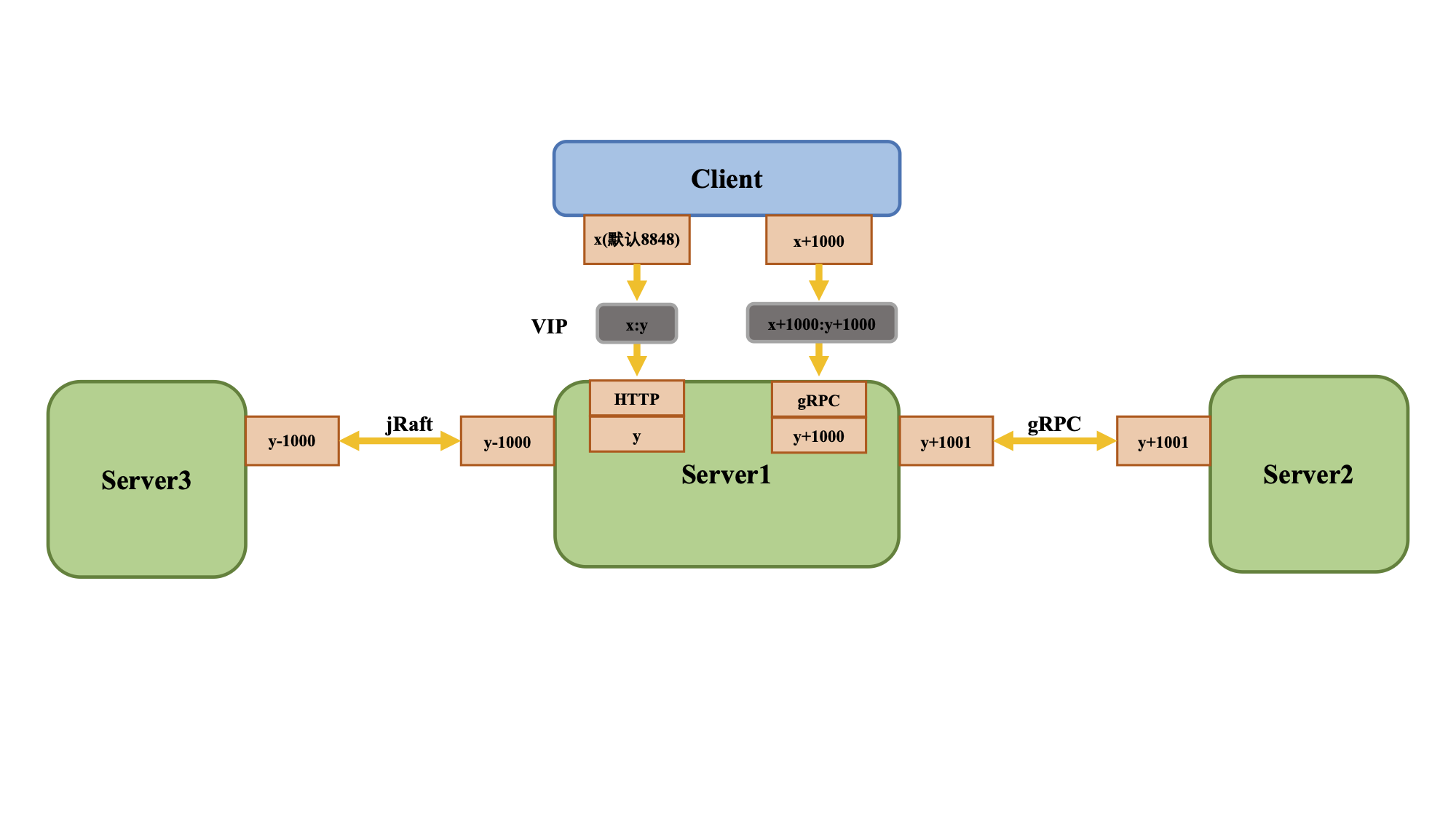
Alibaba Nacos注册中心实战
为什么需要注册中心 思考:网络请求,如果服务提供者发生变动,服务调用者如何感知服务提供者的ip和端口变化? // 微服务之间通过RestTemplate调用,ip:port写死,如果ip或者port变化呢? String ur…...

京东数据采集与挖掘(京东大数据):2023年10月京东冰箱品牌销售排行榜
鲸参谋监测的京东平台10月份冰箱市场销售数据已出炉! 10月份,冰箱市场的销售额有小幅上涨。鲸参谋数据显示,在京东平台上,今年10月冰箱市场的销量为94万,销售额将近23亿,同比增长超过1%。从价格上看&#x…...

某事业单位转型二类后绩效项目成功案例纪实
——事业单位从公益一类转向二类之后,如何通过绩效考核提高人员积极性 【客户行业】事业单位 【问题类型】绩效管理 【客户背景】 某国家级博物馆是由当地ZF与自然资源局共建共管的事业单位,是一家综合性较强的博物馆,入选过全国热搜博物…...

MySQL 和 SQL Server之间的数据迁移方法
目录 MySQL导入SQL Server 使用 SQL Server Management Studio (SSMS) 导入导出向导: 使用 SQL Server Integration Services (SSIS): SQL Server 导入 MySQL 使用 SQL Server Management Studio (SSMS) 导出数据: 使用 MySQL Workbench…...
普通类的测试)
单元测试实战(五)普通类的测试
为鼓励单元测试,特分门别类示例各种组件的测试代码并进行解说,供开发人员参考。 本文中的测试均基于JUnit5。 单元测试实战(一)Controller 的测试 单元测试实战(二)Service 的测试 单元测试实战&am…...

js 迭代器iterator 和 生成器Generator 10
✌ 文章目录 一、迭代器 iterator二、使用步骤1.引入库2.读入数据 总结 一、迭代器 iterator 迭代器是帮助我们对某个数据结构进行遍历的对象 迭代器:是一个对象,帮助我们对某个数据结构进行遍历 迭代器要符合迭代器协议,必须要有一个特定的n…...

100套Axure RP大数据可视化大屏模板及通用组件库
106套Axure RP大数据可视化大屏模板包括了多种实用美观的可视化组件库及行业模板库,行业模板涵盖:金融、教育、医疗、政府、交通、制造等多个行业提供设计参考。 随着大数据的发展,可视化大屏在各行各业得到越来越广泛的应用。可视化大屏不再…...
】)
【OpenGauss源码学习 —— 执行算子(Append算子)】
执行算子(Append算子) Append 算子ExecInitAppend 函数exec_append_initialize_next 函数ExecAppend 函数ExecEndAppend 函数ExecReScanAppend 函数 声明:本文的部分内容参考了他人的文章。在编写过程中,我们尊重他人的知识产权和…...
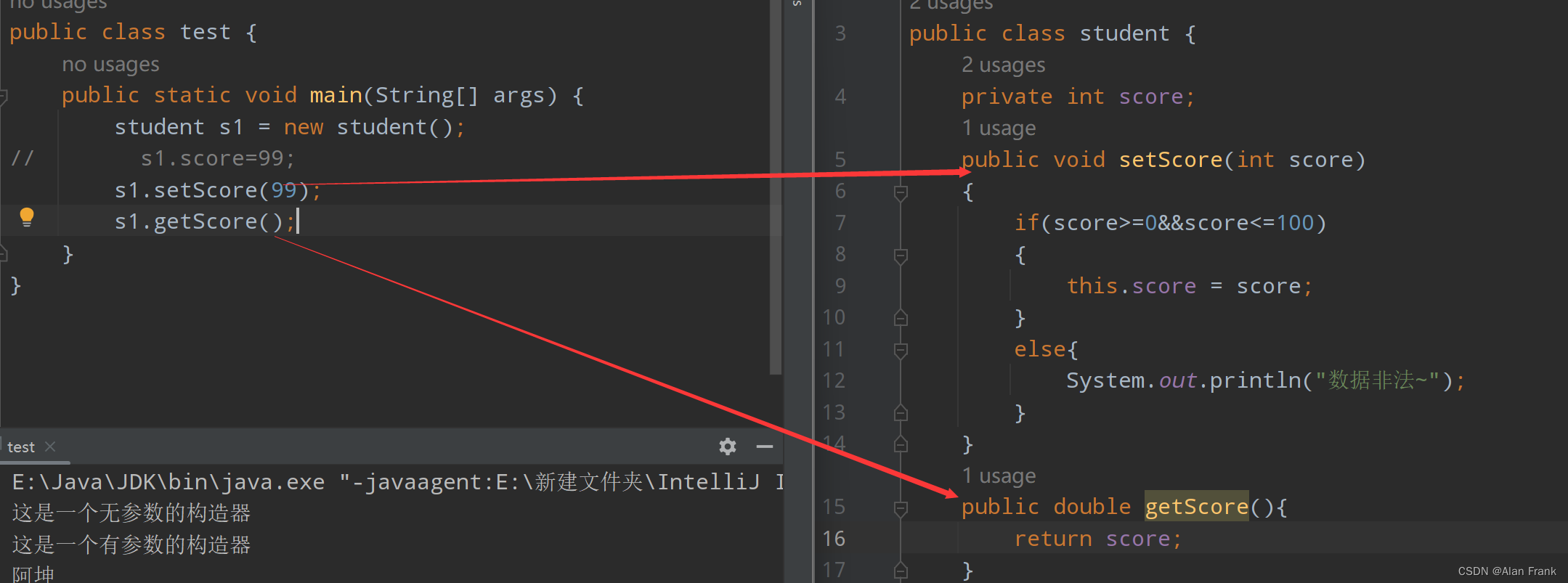
Java(一)(引用类型的参数在传递,方法重载,面向对象编程基础)
基本类型和引用类型的参数在传递的时候有什么不同? 基本类型的值传递:参数传输存储的数据值 引用类型的值传递:参数传输存储的地址值 传递数组名字的时候,传递的是数组的地址,change方法可以通过地址直接访问我们在堆内存中开辟的数组,然后改变数组,数组中的元素发生变化 方…...

Vue第1天:特性概览
文章目录 Vue.js 简介 Vue的特性 如何使用Vue 安装Vue 通过CDN引入 使用npm 创建Vue实例 结语 Vue.js 简介 Vue.js(通常简称为Vue)是一款流行的JavaScript框架,专注于构建用户界面。它的设计灵感来自于现代的JavaScript框架…...

C++语法基础知识面经汇总
背景:汇总了网上C常考的基础知识,方便复习 1,static关键字 static可以用于成员变量,或者成员函数。存储空间在静态存储区(编译器会将其初始化为0,对应的存储空间直到程序执行结束才会释放)&…...

AM@幂级数性质@幂级数和函数求解
文章目录 幂级数性质四则运算性质分析性质求解和函数例例 幂级数性质 和多项式有相似的性质本文介绍用幂级数的性质求解幂级数和函数的两个例子 四则运算性质 若幂级数 ∑ n 0 ∞ a n x n \sum_{n0}^{\infin}a_{n}x^{n} ∑n0∞anxn(1)的收敛半径为 R 1 R_1 R1,和函数为…...

PHP低版本安全问题
目录 1、PHP弱类型问题 1.1 MD5、 SHA1 弱比较问题 1.2 数组 0 1)函数无法处理数组,返回0 2)strcmp 2、特殊字符串导致的问题 2.1 "ffifdyop" 与 md5(string,raw) 2.2 ereg函数漏洞:00 截断 3、正则匹配问…...

结构体——C语言初阶
一.结构体的声明: (1)结构的基础知识: 结构体是一种构造数据类型把不同类型的数据组合成一个整体结构体是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量需要注意的是,结构体是一种…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
