Matalab插值详解和源码
转载:Matalab插值详解和源码 - 知乎 (zhihu.com)
插值法
插值法又称“内插法”,是利用函数f (x)在某区间中已知的若干点的函数值,作出适当的特定函数,在区间的其他点上用这特定函数的值作为函数f (x)的近似值,这种方法称为插值法。如果这特定函数是多项式,就称它为插值多项式。常见分段线性插值法和样条差值,样条插值误差更小。
1 线性插值法
线性插值法是指使用连接两个已知量的直线来确定在这两个已知量之间的一个未知量的值的方法。 假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的y值。根据图中所示,我们得到两点式直线方程:
![]()

假设方程两边的值为α,则:
![]()
![]()
则:y = y0 + α(y1 − y0)(即已知x就可得a值 然后再得y值。
实际上,即使x不在x0到x1之间并且α也不是介于0到1之间,这个公式也是成立的。在这种情况下,这种方法叫作线性外插—参见外插值。
已知y求x的过程与以上过程相同。
2 样条插值法
常用三次样条插值法,具体概念比较复杂,可以自行百度。
3 拉格朗日差值法
略。
- MATLAB中的使用-interp1函数:
MATLAB中的插值函数为interp1,其调用格式为: yi=interp1(x,y,xi,'method') 其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量,
'method'表示采用的插值方法,MATLAB提供的插值方法有几种:
'nearest'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'pchip'立方插值.缺省时表示线性插值
注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
x = 0:2*pi;
y = sin(x);
xx = 0:0.5:2*pi; % interp1对sin函数进行分段线性插值,调用interp1的时候,默认的是分段线性插值
y1 = interp1(x,y,xx,'linear');
subplot(2,2,1);
plot(x,y,'o',xx,y1,'r')
title('分段线性插值') % 临近插值
y2 = interp1(x,y,xx,'nearest');
subplot(2,2,2);
plot(x,y,'o',xx,y2,'r');
title('临近插值') %球面线性插值
y3 = interp1(x,y,xx,'spline');
subplot(2,2,3);
plot(x,y,'o',xx,y3,'r')
title('球面插值') %三次多项式插值法
y4 = interp1(x,y,xx,'pchip');
subplot(2,2,4);
plot(x,y,'o',xx,y4,'r');
title('三次多项式插值') 
例:环境温度
例如:在一 天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为
12,9,9,1,0,18 ,24,28,27,25,20,18,15,13,
推测中午1点(即13点)时的温度.
x = 0:2:24;
y = [12 9 9 10 18 24 28 27 25 20 18 15 13];
a = 13;
y1 = interp1(x,y,a,'spline')
% 结果为: 27.8725 % 若要得到一天24小时的温度曲线,则:
xi = 0:1/3600:24;
% 插值点可以是向量,则返回的也就是对应的向量
yi = interp1(x,y,xi, 'spline');
plot(x,y,'o' ,xi,yi); 
一天24小时温度曲线
| 语法形式 | 说明 |
|---|---|
| y=interp1(x,Y,xi) | 由已知点集(x,Y)插值计算xi上的函数值 |
| y=interp1(Y,xi) | 相当于x=1:length(Y)的interp(x,Y,xi) |
| y=interp1(x,Y,xi,method) | 用指定插值方法计算插值点xi上的函数值 |
| y=interp1(x,Y,xi,method,’pp’) | 用指定方法插值,但返回结果为分段多项式 |
| Method | 方法描述 |
|---|---|
| ‘nearest’ | 最邻近插值:插值点处函数值与插值点最邻近的已知点函数值相等 |
| ‘liner’ | 分段线性插值:插值点处函数值由连接其最邻近的两侧点的线性函数预测。Matlab中interp1的默认方法。 |
| ‘spline’ | 样条插值:默认为三次样条插值。可用spline函数替代即y=spline(x0,y0,x) |
| ‘pchip’ | 三次Hermite多项式插值,可用pchip函数替代 |
| ‘cubic’ | 同’pchip’,三次Hermite多项式插值 |
- Csape函数
csape函数的用法如下:
pp = csape(x,y,conds,valconds)
其中(x,y)为数据向量,conds表示变界类型, valconds表示边界值。
边界类型(conds)可为:
'complete',给定边界 一阶导数.
'not-a-knot',非扭结条件,不用给边界值.
'periodic', 周期性边界条件,不用给边界值.
'second',给定边界二阶导数.
'variational',自然样条(边界二阶导数为0)
边界类型(valconds)可为:
'complete',给定边界 一阶导数.
'not-a-knot',非扭结条件,不用给边界值.
'periodic', 周期性边界条件,不用给边界值.
'second',给定边界二阶导数.
'variational',自然样条(边界二阶导数为0)
例:机床加工
待加工零件的外形根据工艺要求由一组数据(x,y)给出,用程控铣床加工时每一刀只能沿x方向和y方向走非常小的一步,这就需要从已知数据得到加工所要求的步长很小的(x,y)坐标。
依据下表给出的(x,y)数据求x坐标每改变0.1时的y坐标。试完成加工所需数据,画出曲线,并求出x=0处的曲线斜率和13<=x<=15范围内y的最小值。
x 0 3 5 7 9 11 12 13 14 15
y 0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6
x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y1=interp1(x0,y0,x);%分段线性插值 得到x=0:0.1:15相应的函数值向量y1
y2=interp1(x0,y0,x,'spline');%三次样条插值 得到x=0:0.1:15相应的函数值向量y2
pp1=csape(x0,y0);%csape函数三次样条插值,默认边界条件为拉格朗日边界条件
y3=fnval(pp1,x);%得到x=0:0.1:15相应的函数值向量y3
pp2=csape(x0,y0,'second');%设置边界条件为二阶导数,默认为[0,0]
y4=fnval(pp2,x);%得到x=0:0.1:15相应的函数值向量y4
[x',y1',y2',y3',y4'];%得到一个151*4的矩阵可以观察y1,y2,y3,y4随x的变化subplot(1,3,1)%将当前图窗分为1*3网络并在1处创建坐标区(即当前选定1区绘图)
plot(x0,y0,'+',x,y1);%(x0,y0)所代表的点用+表示
title('分段线性插值');subplot(1,3,2)%选定2区绘图
plot(x0,y0,'+',x,y2);
title('三次样条插值-interp1函数')subplot(1,3,3)%选定3区绘图
plot(x0,y0,'+',x,y3);
title('三次样条插值-scape函数')%求x=0处斜率
dx=diff(x);%dx即∆x
dy=diff(y3);%dy即∆y
dy_dx=dy./dx;%(./ 对应元素相除)
dy_dx0=dy_dx(1);%x=0处的导数就是dy./dx的第一个元素:dy0/dx0%求13<=x<=15范围内y的最小值
ytemp=y3(131:151);%取出13<=x<=15区间内对应的y3值(因为y3误差更小,数据分析更准确)
ymin=min(ytemp);
index=find(y3==ymin);%y3中最小值对应的序列
xmin=x(index);%并由序列找到对应的x值
[xmin,ymin]%输出运行程序:
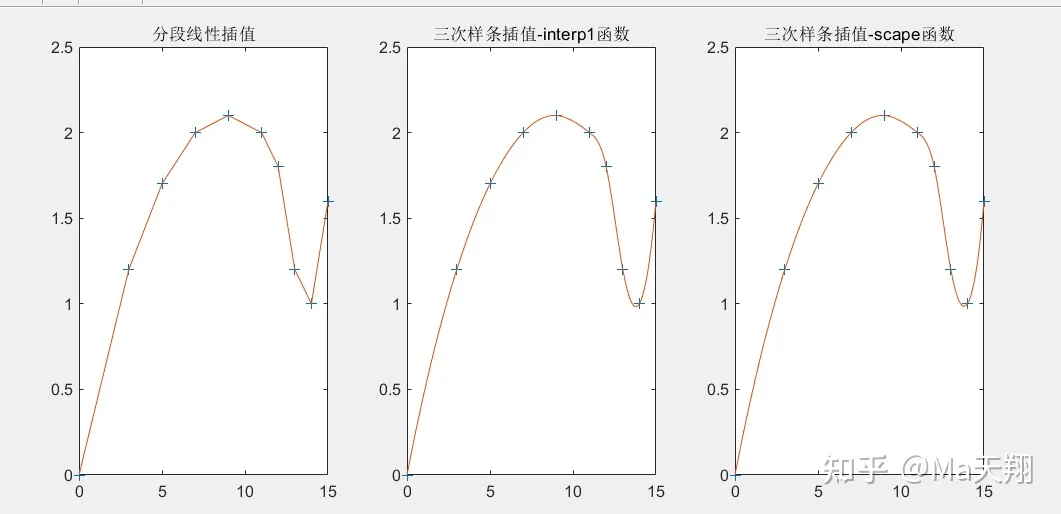
可以看出调用interp1和csape三次样条插值结果相同,同时三次样条插值比分段线性插值更精确。
最小值:
ans = 13.8000 0.9851csape 和interp1有什么相同和区别?
csape和interp1都是插值函数。
csape可以选择样条的边界条件,interp1无法使用边界条件;
csape只是Cubic spline插值,interp1可以选择几种不同的插值方法。
注:本文interp1函数和代码使用部分引用于matlab自带的插值函数interp1的几种插值方法 。个人在原文上修改了一小部分且补充了一点csape函数使用方面,自以为豪得是本文注释讲解做的格外用心.
还有就是上面的案例都是一维插值(插值函数为一元函数),二维插值(插值函数为二元函数-曲面)使用interp2函数或仍使用csape函数,涉及到具体问题得话可以自寻查找相关内容。
参考文献:《数学建模算法与应用》.
相关文章:

Matalab插值详解和源码
转载:Matalab插值详解和源码 - 知乎 (zhihu.com) 插值法 插值法又称“内插法”,是利用函数f (x)在某区间中已知的若干点的函数值,作出适当的特定函数,在区间的其他点上用这特定函数的值作为函数f (x)的近似值,这种方…...

Flask 接口
目录 前言 代码实现 简单接口实现 执行其它程序接口 携带参数访问接口 前言 有时候会想着开个一个接口来访问试试,这里就给出一个基础接口代码示例 代码实现 导入Flask模块,没安装Flask 模块需要进行 安装:pip install flask 使用镜…...
Vue3 toRef函数和toRefs函数
当我们在setup 中的以读取对象属性单独交出去时,我们会发现这样会丢失响应式: setup() {let person reactive({name: "张三",age: 18,job: {type: "前端",salary:10}})return {name: person.name,age: person.age,type: person.jo…...
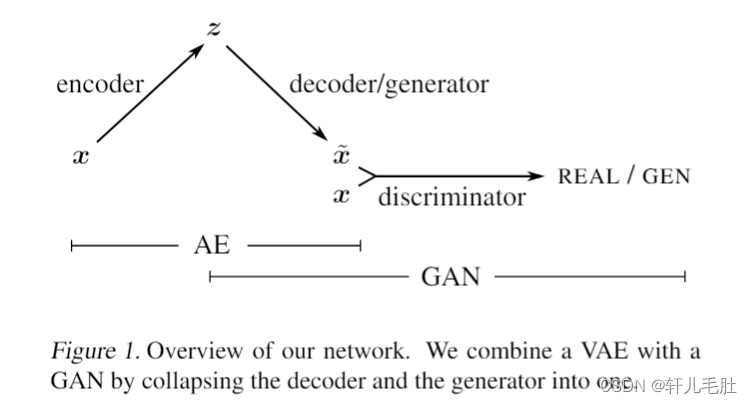
【论文阅读】(VAE-GAN)Autoencoding beyond pixels using a learned similarity metric
论文地址;[1512.09300] Autoencoding beyond pixels using a learned similarity metric (arxiv.org) / 一、Introduction 主要讲了深度学习中生成模型存在的问题,即常用的相似度度量方式(使用元素误差度量)对于学习良好的生成模型存在一定…...

verilog之wire vs reg区别
文章目录 一、wire vs reg二、实例一、wire vs reg wire线网: 仅支持组合逻辑建模必须由assign语句赋值不能在always块中驱动用于连接子模块的输出用于定义模块的输入端口reg寄存器: 可支持组合逻辑或时序逻辑建模必须在always块中赋值二、实例 wire [7:0] cnt; assign cnt …...

力扣面试经典150题详细解析
刷题的初心 众所周知,算法题对于面试大厂是必不可缺的一环,而且对于提高逻辑思维能力有着不小的提升。所以,对于程序员来讲,无论刚入行,还是从业多年,保持一个清醒的头脑,具备一个良好的设计思…...

【Java 进阶篇】唤醒好运:JQuery 抽奖案例详解
在现代社交网络和电商平台中,抽奖活动成为吸引用户、提升用户参与度的一种常见手段。通过精心设计的抽奖页面,不仅可以增加用户的互动体验,还能在一定程度上提高品牌的知名度。本篇博客将通过详细解析 JQuery 抽奖案例,带领你走进…...

数据处理生产环境_利用MurmurHash3算法在Spark和Scala中生成随机颜色
需求 根据给定的轨迹编号在这一列后面生成随机颜色_16 输入数据 ("吃饭", "123"), ("吃饭", "宋江"), ("郭靖", "宋江"), ("杨过", "奥特曼"), ("周芷若", "张无忌"),…...

便利工具分享:一个proto文件的便利使用工具
最近在研究序列化,每次的proto文件手敲生成代码指令都很麻烦,干脆自己写一个泛用脚本,这样以后使用时候就方便了。 废话不多说,首先上代码: #!/bin/bash # 检查是否提供了文件名参数 if [ -z "$1" ]; then…...
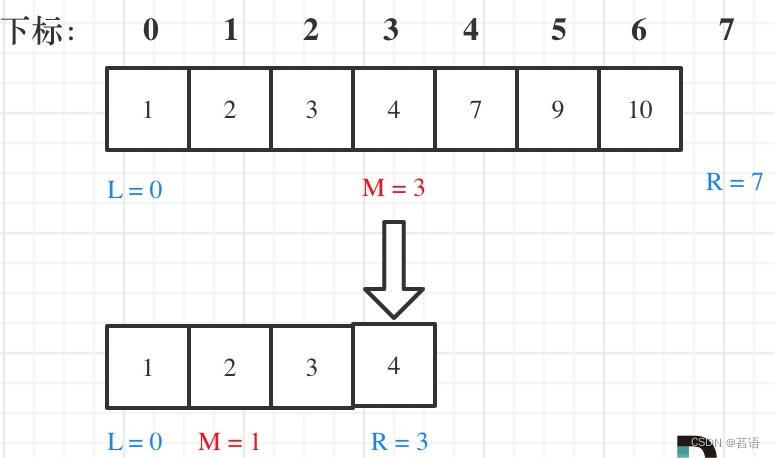
LeetCode704.二分查找及二分法
每日一题:LeetCode704.二分查找 LeetCode704.二分查找知识点:二分法解题代码 LeetCode704.二分查找 问题描述:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中…...
2023年R1快开门式压力容器操作证模拟考试题库及R1快开门式压力容器操作理论考试试题
题库来源:安全生产模拟考试一点通公众号小程序 2023年R1快开门式压力容器操作证模拟考试题库及R1快开门式压力容器操作理论考试试题是由安全生产模拟考试一点通提供,R1快开门式压力容器操作证模拟考试题库是根据R1快开门式压力容器操作最新版教材&#…...

探索NLP中的核心架构:编码器与解码器的区别
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
解决:Error: Missing binding xxxxx\node_modules\node-sass\vendor\win32-x64-83\
一、具体报错 二、报错原因 这个错误是由于缺少 node-sass 模块的绑定文件引起的。 三、导致原因 3.1、环境发生了变化 3.2、安装过程出现问题 四、解决方法步骤: 4.1、重新构建 node-sass 模块 npm rebuild node-sass 4.2、清除缓存并重新安装依赖 npm c…...

科研学习|科研软件——面板数据、截面数据、时间序列数据的区别是什么?
一、数据采集方式不同 面板数据是通过在多个时间点上对同一组体进行观测而获得的数据。面板数据可以是横向面板数据,即对同一时间点上不同个体的观测,也可以是纵向面板数据,即对同一个体在不同时间点上的观测。采集面板数据需要跟踪相同的个体…...

【UE5】物体沿样条线移动
目录 效果 步骤 一、使用样条线创建路径 二、创建沿样条线路径移动的物体 三、定义可移动物体的生成器 效果 步骤 一、使用样条线创建路径 先创建一个Actor蓝图,这里命名为“BP_Line” 该蓝图中只需添加一个样条组件 将“BP_Line”拖入场景中 按住Alt鼠标左键…...
Qt控件按钮大全
按钮 在 Qt 里,最常用使用的控件就是按钮了,有了按钮,我们就可以点击,从而响应事件,达到人机交互的效果。不管是嵌入式或者 PC 端,界面交互,少不了按钮。Qt 按钮部件是一种常用的部件之一,Qt 内置了六种按钮部件如下: (1) QPushButton:下压按钮 (2) QToolBu…...
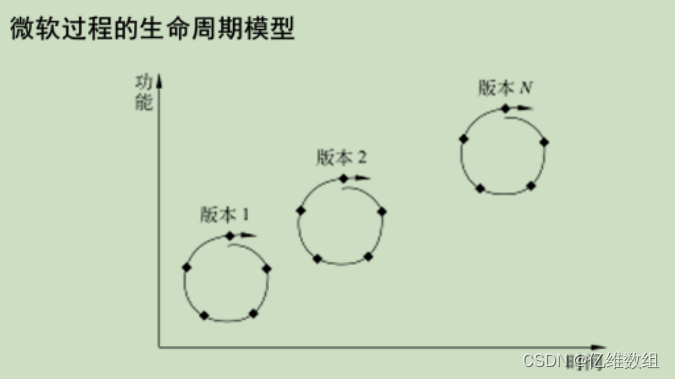
软件工程--软件过程学习笔记
本篇内容是对学校软件工程课堂内容的记录总结,部分也来源于网上查找的资料 软件过程基础 软件过程是指在软件开发过程中,经过一系列有序的步骤和活动,从问题定义到最终软件产品交付和维护的全过程。这个过程旨在确保软件项目能够按时、按预…...
高校教师资格证备考
高等教育制度 关于人的全面发展和个体发展的关系,说法正确的是(ABC)。 A.个体发展是在全面发展基础上的选择性发展 B.全面发展是个体发展的前提和基础 C.个体发展又是全面发展的动力 D.个体发展是全面发展的前提和基础...

Git通过rebase合并多个commit
在使用 Git 作为版本控制的时候,我们可能会由于各种各样的原因提交了许多临时的 commit,而这些 commit 拼接起来才是完整的任务。那么我们为了避免太多的 commit 而造成版本控制的混乱,通常我们推荐将这些 commit 合并成一个。 1. 查看提交历…...
ROS 学习应用篇(八)ROS中的坐标变换管理之tf广播与监听的编程实现
偶吼吼胜利在望,冲冲冲 老规矩新建功能包 工作空间目录下/src下开启终端输入 catkin_create_pkg learning_tf roscpp rospy tf turtlesim 如何实现tf广播 引入库 c python …...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
