机器学习第5天:多项式回归与学习曲线
文章目录
多项式回归介绍
方法与代码
方法描述
分离多项式
学习曲线的作用
场景
学习曲线介绍
欠拟合曲线
示例
结论
过拟合曲线
示例
结论
多项式回归介绍
当数据不是线性时我们该如何处理呢,考虑如下数据
import matplotlib.pyplot as plt
import numpy as npnp.random.seed(42)x = 8 * np.random.rand(100, 1) - 4
y = 2*x**2+3*x+np.random.randn(100, 1)plt.scatter(x, y)
plt.show()
方法与代码
方法描述
先讲思路,以这个二元函数为例
将多项式化为多个单项的,也就是将x的平方和x两个项分离开,然后单独给线性模型处理,求出参数,最后再组合在一起,很好理解,让我们来看一下代码
分离多项式
我们使用机器学习库的PolynomialFeatures来分离多项式
from sklearn.preprocessing import PolynomialFeaturespoly_features = PolynomialFeatures(degree=2, include_bias=False)
x_poly = poly_features.fit_transform(x)
print(x[0])
print(x_poly[0])运行结果

可以看到,4, 5行代码将原始x和x平方挑选了出来,这时我们再把这个数据进行线性回归
model = LinearRegression()
model.fit(x_poly, y)
print(model.coef_)这段代码使用处理后的x拟合y,再打印模型拟合的参数,可以看到模型的两个参数分别是2.9和2左右,而我们的方程的一次参数和二次参数分别是3和2,可见效果还是很好的
![]()
把预测的结果绘制出来
model = LinearRegression()
model.fit(x_poly, y)
pre_y = model.predict(x_poly)# 这里是为了让x升序的排序算法, 可以尝试不加这段代码图会变成什么样
sorted_indices = sorted(range(len(x)), key=lambda k: x[k])
x_sorted = [x[i] for i in sorted_indices]
y_sorted = [pre_y[i] for i in sorted_indices]plt.plot(x_sorted, y_sorted, "r-")
plt.scatter(x, y)
plt.show()
学习曲线的作用
场景
设想一下,当你需要预测房价,你也有多组数据,包括离学校距离,交通状况等,但是问题来了,你只知道这些特征可能与房价有关,但并不知道这些特征与房价之间的方程关系,这时我们进行回归任务时,就可能导致欠拟合或者过拟合,幸运的是,我们可以通过学习曲线来判断
学习曲线介绍
学习曲线图就是以损失函数为纵坐标,数据集大小为横坐标,然后在图上画出训练集和验证集两条曲线的图,训练集就是我们用来训练模型的数据,验证集就是我们用来验证模型性能的数据集,我们往往将数据集分成训练集与验证集
我们先定义一个学习曲线绘制函数
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegressiondef plot_learning_curves(model, x, y):x_train, x_val, y_train, y_val = train_test_split(x, y, test_size=0.2)train_errors, val_errors = [], []for m in range(1, len(x_train)):model.fit(x_train[:m], y_train[:m])y_train_predict = model.predict(x_train[:m])y_val_predict = model.predict(x_val)train_errors.append(mean_squared_error(y_train[:m], y_train_predict))val_errors.append(mean_squared_error(y_val, y_val_predict))plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")plt.legend()plt.show() 简单介绍一下,这个函数接收模型参数,x,y参数,然后在for循环中,取不同数据集大小来计算RMSE损失(就是),然后把曲线绘制出来
欠拟合曲线
我们知道欠拟合就是模拟效果不好的情况,可以想象的到,无论在训练集还是验证集上,他的损失都会比较高
示例
我们将线性模型的学习曲线绘制出来
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegressiondef plot_learning_curves(model, x, y):x_train, x_val, y_train, y_val = train_test_split(x, y, test_size=0.2)train_errors, val_errors = [], []for m in range(1, len(x_train)):model.fit(x_train[:m], y_train[:m])y_train_predict = model.predict(x_train[:m])y_val_predict = model.predict(x_val)train_errors.append(mean_squared_error(y_train[:m], y_train_predict))val_errors.append(mean_squared_error(y_val, y_val_predict))plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")plt.legend()plt.show()x = np.random.rand(100, 1)
y = 2 * x + np.random.rand(100, 1)model = LinearRegression()
plot_learning_curves(model, x, y)

结论
可以看到,在只有一点数据时,模型在训练集上效果很好(因为就是开始这一些数据训练出来的),而在验证集上效果不好,但随着训练集增加(模型学习到的越多),验证集上的误差逐渐减小,训练集上的误差增加(因为是学到了一个趋势,不会完全和训练集一样了)
这个图的特征是两条曲线非常接近,且误差都较大(差不多在0.3) ,这是欠拟合的表现(模型效果不好)
过拟合曲线
过拟合就是完全以数据集来模拟曲线,泛化能力很差
示例
我们来试试将一次函数模拟成三次函数,再来看看学习曲线(毫无疑问过拟合了)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipelinedef plot_learning_curves(model, x, y):x_train, x_val, y_train, y_val = train_test_split(x, y, test_size=0.2)train_errors, val_errors = [], []for m in range(1, len(x_train)):model.fit(x_train[:m], y_train[:m])y_train_predict = model.predict(x_train[:m])y_val_predict = model.predict(x_val)train_errors.append(mean_squared_error(y_train[:m], y_train_predict))val_errors.append(mean_squared_error(y_val, y_val_predict))plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")plt.legend()plt.show()np.random.seed(10)
x = np.random.rand(200, 1)
y = 2 * x + np.random.rand(200, 1)poly_regression = Pipeline([("Poly", PolynomialFeatures(degree=3, include_bias=False)),("Line", LinearRegression())
])plot_learning_curves(poly_regression, x, y)
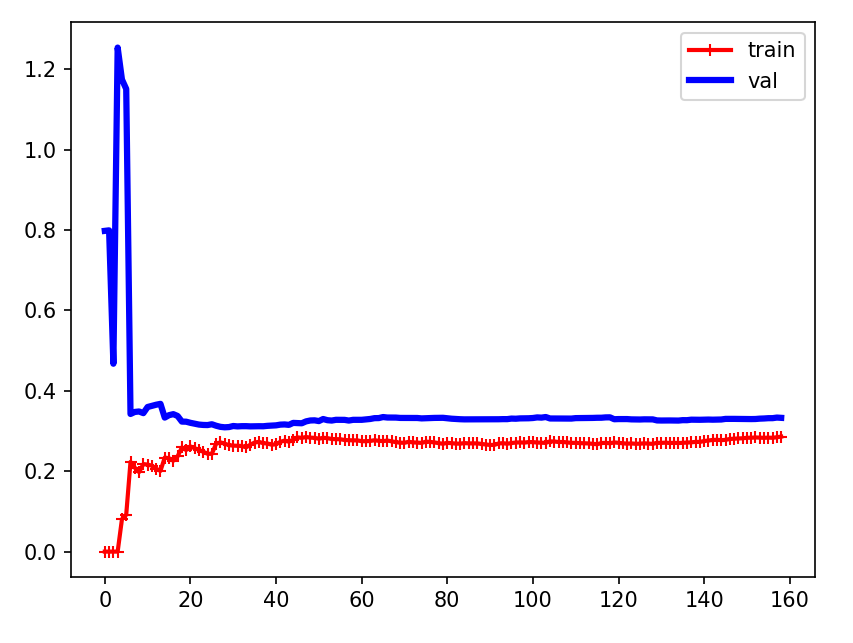 结论
结论
这条曲线的特征是训练集的效果比验证集好(两条线之间有一定间距),这往往是过拟合的表现(在训练集上效果好,验证集差,表面泛化能力差)
相关文章:

机器学习第5天:多项式回归与学习曲线
文章目录 多项式回归介绍 方法与代码 方法描述 分离多项式 学习曲线的作用 场景 学习曲线介绍 欠拟合曲线 示例 结论 过拟合曲线 示例 结论 多项式回归介绍 当数据不是线性时我们该如何处理呢,考虑如下数据 import matplotlib.pyplot as plt impo…...
MSYS2介绍及工具安装
0 Preface/Foreword 1 MSYS2 官网:MSYS2...

Swift开发中:非逃逸闭包、逃逸闭包、自动闭包的区别
1. 非逃逸闭包(Non-Escaping Closure) 定义:默认情况下,在 Swift 中闭包是非逃逸的。这意味着闭包在函数结束之前被调用并完成,它不会“逃逸”出函数的范围。内存管理:由于闭包在函数返回前被调用…...

栈结构应用-进制转换-辗转相除法
// 定义类class Stack{// #items [] 前边加#变为私有 外部不能随意修改 内部使用也要加#items []pop(){return this.items.pop()}push(data){this.items.push(data)}peek(){return this.items[this.items.length-1]}isEmpty(){return this.items.length 0}size(){return th…...
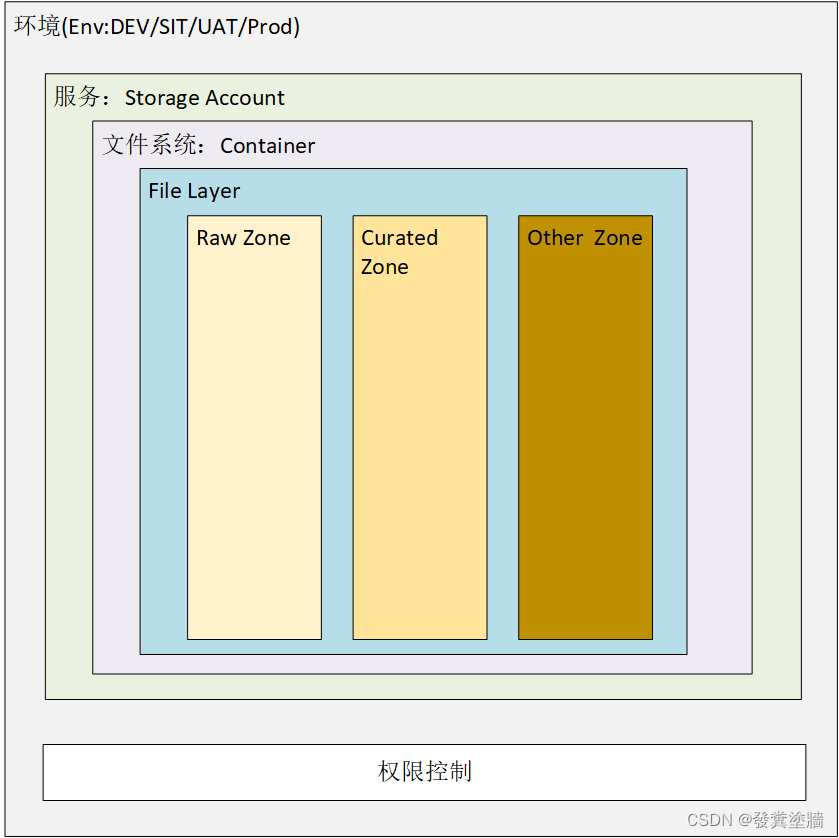
【Azure 架构师学习笔记】-Azure Storage Account(6)- File Layer
本文属于【Azure 架构师学习笔记】系列。 本文属于【Azure Storage Account】系列。 接上文 【Azure 架构师学习笔记】-Azure Storage Account(5)- Data Lake layers 前言 上一文介绍了存储帐户的概述,还有container的一些配置,在…...
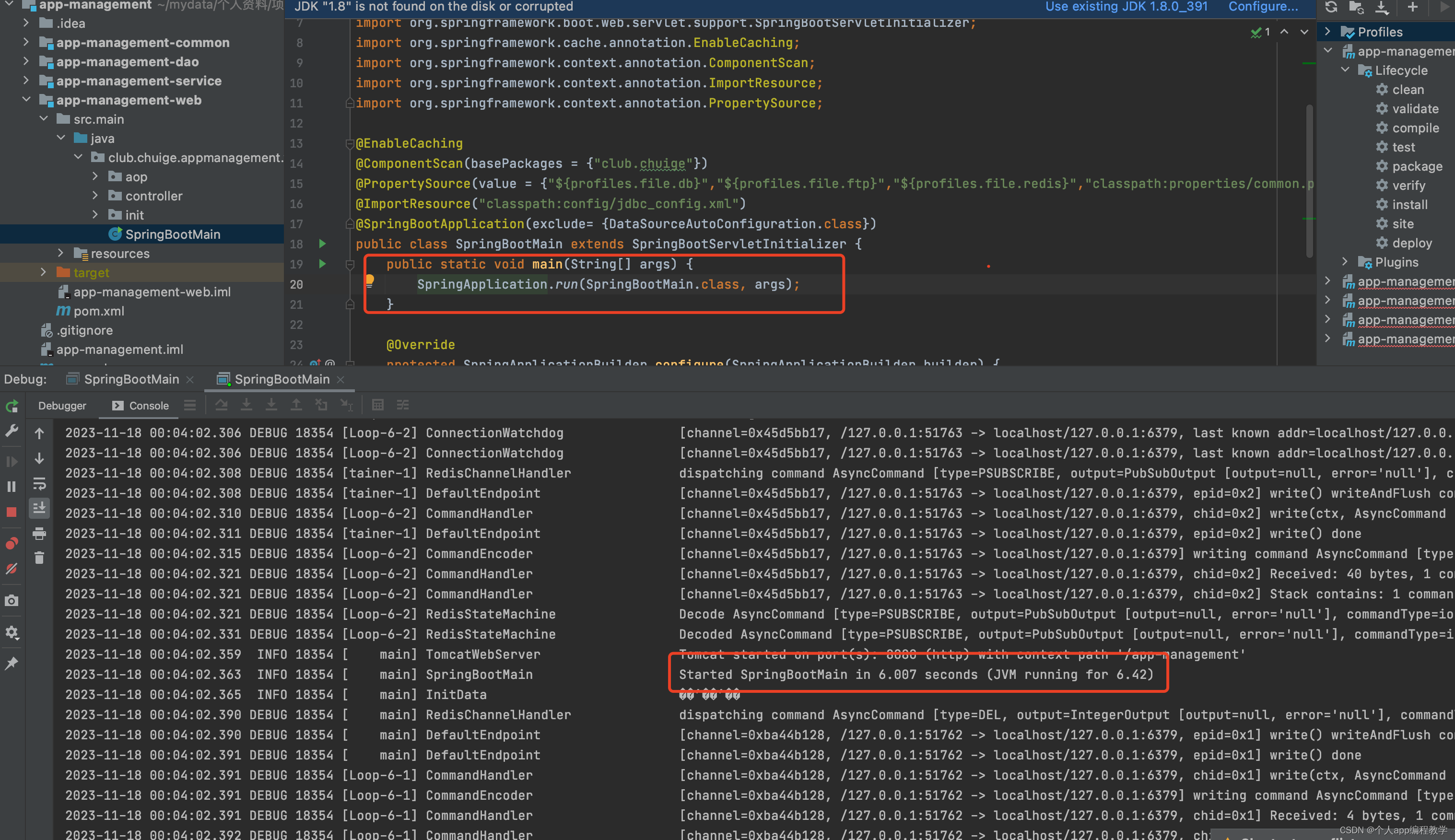
idea 环境搭建及运行java后端源码
1、 idea 历史版本下载及安装 建议下载和我一样的版本,2020.3 https://www.jetbrains.com/idea/download/other.html,idea分为专业版本(Ultimate)和社区版本(Community),前期可以下载专业版本…...
掌握Shell:从新手到编程大师的Linux之旅
1 shell介绍 1.1 shell脚本的意义 1.记录命令执行的过程和执行逻辑,以便以后重复执行 2.脚本可以批量处理主机 3.脚本可以定时处理主机 1.2 脚本的创建 #!/bin/bash # 运行脚本时候执行的环境1.3 自动添加脚本说明信息 /etc/vimrc # vim主配置文件 ~/.vimrc # 该…...

有重复元素的快速排序
当涉及到处理重复元素的快速排序时,可以使用荷兰国旗问题的方法,也就是三路划分。下面是使用 Java 实现的示例代码: import java.util.Arrays;public class QuickSort {public static void quickSort(int[] arr, int low, int high) {if (lo…...

Bert浅谈
优点 首先,bert的创新点在于利用了双向transformer,这就跟openai的gpt有区别,gpt是采用单向的transformer,而作者认为双向transformer更能够融合上下文的信息。这里双向和单向的区别在于,单向只跟当前位置之前的tocke…...

产品运营的场景和运营策略
一、启动屏 1.概念 启动屏,特指 APP 产品启动时即显示的界面,这个界面一般会停留几秒钟时间,在这个时间内 APP 会在后台加载服务框架、启动各种服务 SDK 、获取用户地理位置、判断有无新版本、判断用户账户状态以及其他系统级别的…...

C#异常捕获try catch详细介绍
在C#中,异常处理是通过try、catch、finally和throw语句来实现的,它们提供了一种结构化和可预测的方法来处理运行时错误。 C#异常基本用法 try块 异常处理以try块开始,try块包含可能会引发异常的代码。如果在try块中的代码执行过程中发生了…...

切换阿里云ES方式及故障应急处理方案
一、阿里云es服务相关问题及答解 1.1 ES7.10扩容节点时间 增加节点数量需要节点拉起和数据Rebalance两步,拉起时间7.16及以上的新版本大概10分钟以内,7.16以前大概一小时,数据迁移的时间就看数据量了,一般整体在半小时以内 (需进行相关测试验证) 1.2 ES7.10扩容数据节点…...
CTFhub-RCE-过滤空格
1. 查看当前目录:127.0.0.1|ls 2. 查看 flag_890277429145.php 127.0.0.1|cat flag_890277429145.php 根据题目可以知道空格被过滤掉了 3.空格可以用以下字符代替: < 、>、<>、%20(space)、%09(tab)、$IFS$9、 ${IFS}、$IFS等 $IFS在li…...

无需添加udid,ios企业证书的自助生成方法
我们开发uniapp的app的时候,需要苹果证书去打包。 假如申请的是个人或company类型的苹果开发者账号,必须上架才能安装,异常的麻烦,但是有一些app,比如企业内部使用的app,是不需要上架苹果应用市场的。 假…...

【PTA题目】6-20 使用函数判断完全平方数 分数 10
6-20 使用函数判断完全平方数 分数 10 全屏浏览题目 切换布局 作者 张高燕 单位 浙大城市学院 本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare( int n ); 其中n是用户传入的参数,在长整型范围内。如果n是完全…...
Nas搭建webdav服务器并同步Zotero科研文献
无需云盘,不限流量实现Zotero跨平台同步:内网穿透私有WebDAV服务器 文章目录 无需云盘,不限流量实现Zotero跨平台同步:内网穿透私有WebDAV服务器一、Zotero安装教程二、群晖NAS WebDAV设置三、Zotero设置四、使用公网地址同步Zote…...

一句话总结敏捷实践中不同方法
敏捷实践是指一组优先考虑灵活性、协作和客户满意度的软件开发和项目管理原则和方法。 不同方法论的敏捷实践: 1、敏捷: Sprints:限时迭代(通常 2-4 周),在此期间创建潜在的可交付产品增量。每日站立会议…...

【数据结构】线段树(点修区查)
数据结构-线段树(点修区查) 前置知识 分治递归二叉树 思路 我们需要维护一个支持单点修改,区间查询的数据结构,并且要求在线,一般使用线段树解决。 线段树是一个二叉树形的数据结构。 线段树的思想很简单,…...
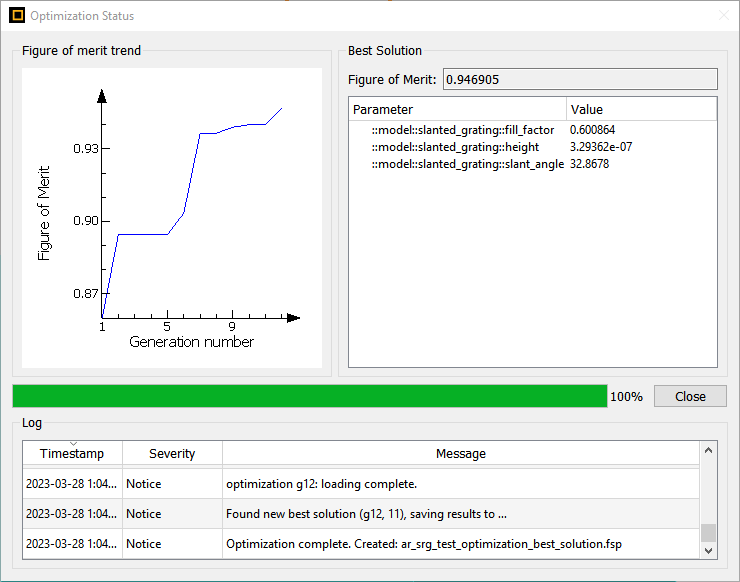
Ansys Lumerical | 用于增强现实系统的表面浮雕光栅
在本示例中,我们使用 RCWA 求解器设计了一个斜面浮雕光栅 (SRG),它将用于将光线耦合到单色增强现实 (AR) 系统的波导中。光栅的几何形状经过优化,可将正常入射光导入-1 光栅阶次。 然后我们将光栅特性导出为 Lumerical Sub-Wavelength Model …...

QT day3作业
1.思维导图 2、 完善对话框,点击登录对话框,如果账号和密码匹配,则弹出信息对话框,给出提示”登录成功“,提供一个Ok按钮,用户点击Ok后,关闭登录界面,跳转到其他界面 如果账号和密…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
