golang学习笔记——斐波纳契数列
斐波纳契数列

编写一个程序来计算某个数字的斐波纳契数列。
斐波那契数列是一个数字列表,其中每个数字是前两个斐波那契数字之和。 例如,数字 6 的序列是 1,1,2,3,5,8,数字 7 的序列是 1,1,2,3,5,8,13,数字 8 的序列是 1,1,2,3,5,8,13,21,以此类推。
package mainimport "fmt"func fibonacci(n int) []int {if n < 2 {return make([]int, 0)}nums := make([]int, n)nums[0], nums[1] = 1, 1for i := 2; i < n; i++ {nums[i] = nums[i-1] + nums[i-2]}return nums
}func main() {var num intfmt.Print("What's the Fibonacci sequence you want? ")fmt.Scanln(&num)fmt.Println("The Fibonacci sequence is:", fibonacci(num))
}
测试,输入13
The Fibonacci sequence is: [1 1 2 3 5 8 13 21 34 55 89 144 233]
相关文章:

golang学习笔记——斐波纳契数列
斐波纳契数列 编写一个程序来计算某个数字的斐波纳契数列。 斐波那契数列是一个数字列表,其中每个数字是前两个斐波那契数字之和。 例如,数字 6 的序列是 1,1,2,3,5,8,数字 7 的序列是 1,1,2,3,5,8,13,数字 8 的序列是 1,1,2,3,5…...
)
学习raft协议(1)
CAP C: 一致性 强调数据的正确性,每次读操作,要么读到最新,要么读失败 A:可用性 不发生错误,也不能出现过长的等待时间. P:分区容错性 在网络环境不可靠的背景下,整个系统仍然是正常运作的两种流派 (1&am…...

SpringSecurity+jwt使用
参考文章链接 自定义SpringSecurity用户 package com.daben.springsecurityjwt.vo;import com.daben.springsecurityjwt.entity.SysUser; import org.springframework.security.core.GrantedAuthority; import org.springframework.security.core.userdetails.User; import j…...

html-网站菜单-点击显示导航栏
一、效果图 1.点击显示菜单栏,点击x号关闭; 2.点击一级菜单,展开显示二级,并且加号变为减号; 3.点击其他一级导航,自动收起展开的导航。 二、代码实现 <!DOCTYPE html> <html><head>&…...

【C++函数的进化】函数指针,模板,仿函数,lambda表达式
/*** poject * author jUicE_g2R(qq:3406291309)* file C函数的进化* * language C* EDA Base on VS2022* editor Obsidian(黑曜石笔记软件)* * copyright 2023* COPYRIGHT 原创学习笔记:转载需获得博…...

云服务器windows service2022 部署git服务器
1 安装 下载地址gitblit 解压到你的一个目录,我这里给的是C:\gitblit 根据官网提示要下载jre or jdk7.0,这里建议使用下载jre (jdk 有时候运行出问题,或者2个都安装),自行安装java,这里不做环境配置的说明 进入c:\gitblit\data 目录里面找到,defaults.properties 文件,编辑主…...

Linux_Docker修改Docker Root Dir
今天遇到需求,要修改一下docker容器和镜像的存储位置,默认位置为/var/lib/docker目录下,要修改到/new/dockerFile目录下。 停止docker服务 sudo service docker stop 备份docker容器镜像 移动/var/lib/docker目录下的文件到/dockerFile目录…...

解决requests 2.28.x版本SSL错误:证书验证失败
1、问题背景 在使用requests 2.28.1版本时,我进行HTTP post传输报告负载时,由于SSL验证设置为True,请求失败,错误如下:(Caused by SSLError(SSLCertVerificationError(1, ‘[SSL: CERTIFICATE_VERIFY_FAILED] certifi…...

【开源】基于Vue.js的开放实验室管理系统的设计和实现
项目编号: S 013 ,文末获取源码。 \color{red}{项目编号:S013,文末获取源码。} 项目编号:S013,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 实验室类型模块2.2 实验室模块2.3 实…...

使用composer安装ffmpeg的步骤
以下是使用composer安装ffmpeg的步骤: 1.在laravel根目录下执行以下命令安装ffmpeg: composer require php-ffmpeg/php-ffmpeg 2.如果不指定版本号,则默认使用0.14版本。 3.执行以上命令后,composer会自动下载并安装ffmpeg。 …...
,现代倒残差移动模块设计|ICCV2023)
RT-DETR优化策略:轻量级Backbone改进 | 高效模型 (Efficient MOdel, EMO),现代倒残差移动模块设计|ICCV2023
🚀🚀🚀本文改进:面向移动端的轻量化网络模型——EMO,它能够以相对较低的参数和 FLOPs 超越了基于 CNN/Transformer 的 SOTA 模型,支持四个版本EMO_1M, EMO_2M, EMO_5M, EMO_6M,参数量如下,相对于自带的rtdetr-l、rtdetr-x有很大提升 layersparametersgradientsEMO_1…...

一些nginx命令
1.停止nginx nginx -s quit systemctl stop nginx.service 立即停止 nginx-s stop 杀死nginx进程 killall nginx 2.启动命令 nginx systemctl start nginx.service 3.查看nginx进程 ps aux | grep nginx 4.重启nginx服务 systemctl restart nginx.service 5.重载…...

WPF自定义控件介绍
在WPF中,自定义控件通常是指从头开始创建一个新控件或从现有控件继承并扩展其功能。自定义控件与用户控件(User Control)不同,用户控件是通过组合其他控件来构建的,而自定义控件通常涉及对控件的更底层的渲染和行为进行…...

JUNIT使用和注意、以及断言的介绍使用、SpringBoot Test测试类的使用、maven配置使用junit详细介绍
参考文章: https://www.cnblogs.com/zhukaile/p/14514238.html,https://blog.csdn.net/qq_36448800/article/details/126438339 一、什么是单元测试 在平时的开发当中,一个项目往往包含了大量的方法,可能有成千上万个。如何去保…...

强化学习在文生图中的应用:Training Diffusion Models with Reinforcement Learning
论文链接:Training Diffusion Models with Reinforcement Learning项目地址:Training Diffusion Models with Reinforcement Learning官方代码:https://github.com/kvablack/ddpo-pytorch/tree/maintrl实现:https://huggingface.co/docs/trl/ddpo_trainer🤗关注公众号 fu…...
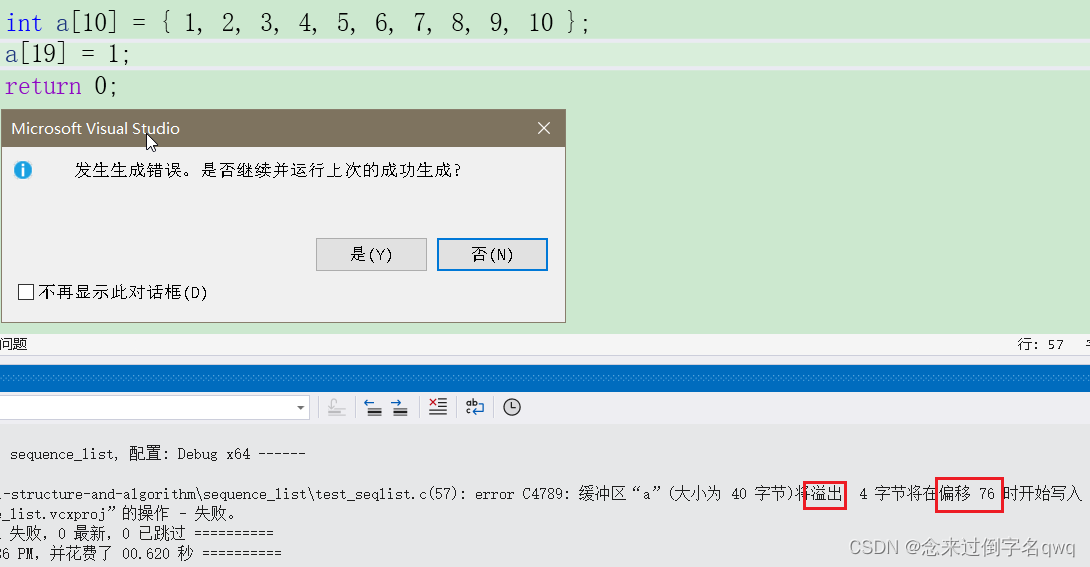
【C语言】数组下标为啥从0开始?下标越界访问一定报错吗?
本篇文章目录 0. 相关文章1. 下标从0开始问题2. 数组下标越界不报错问题 0. 相关文章 指针与指针变量数组名不是首元素地址的的2个例外拨开指针和数组名之间的迷雾 1. 下标从0开始问题 原因是:数组下标访问本质是“指针解引用操作”,而指针又是地址&am…...
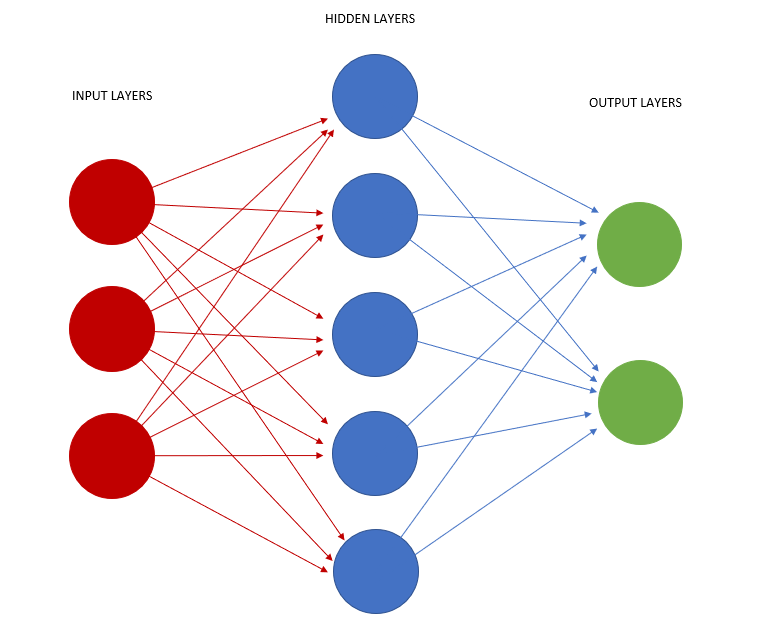
机器学习-搜索技术:从技术发展到应用实战的全面指南
在本文中,我们全面探讨了人工智能中搜索技术的发展,从基础算法如DFS和BFS,到高级搜索技术如CSP和优化问题的解决方案,进而探索了机器学习与搜索的融合,最后展望了未来的趋势和挑战,提供了对AI搜索技术深刻的…...

Axelar、J.P.Morgan Onyx、Apollo 完成概念验证,向跨区块链自动化投资领域探索
J.P.Morgan Onyx、Apollo、Axelar、Oasis Pro 以及 Provenance Block Chain 展开合作,共同进行互操作性概念验证(Proof-of-Concept,PoC)。 新加坡 — Axelar Inc.、Oasis Pro 、Provenance Blockchain 与 J.P.Morgan Onyx 以及 Apollo 通过新…...
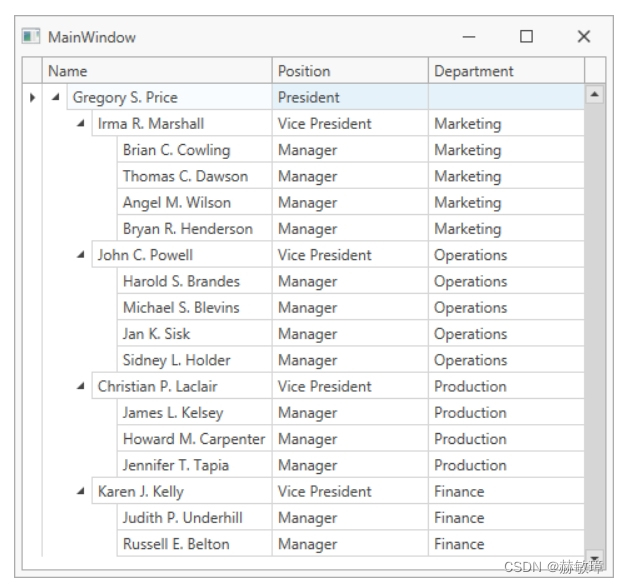
wpf devexpress添加TreeListControl到项目
此教程示范如何添加TreeListControl到项目和绑定控件自引用数据源: 添加数据模型 绑定tree,并添加如下字段到数据源对象: Key字段包含唯一值索引节点 Parent字段包含父索引节点 添加数据模型(Employee和Staff类)到…...

WPF创建自定义控件编译通过但是找不到资源
报错: 原因: 路径写错了: 不是这样: Source"pack://application:,,,/Controls/Styles/xTabControl.xaml" 而是这样: Source"pack://application:,,,/项目名;component/Controls/Styles/xTabControl.xaml …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
