强化学习在文生图中的应用：Training Diffusion Models with Reinforcement Learning
- 论文链接：Training Diffusion Models with Reinforcement Learning
- 项目地址：Training Diffusion Models with Reinforcement Learning
- 官方代码：https://github.com/kvablack/ddpo-pytorch/tree/main
- trl实现：https://huggingface.co/docs/trl/ddpo_trainer
- 🤗关注公众号 funNLPer 分享有用的算法知识🤗
文章目录
- 1. 概述
- 2. 预备知识
- 2.1 扩散模型简介
- 2.2 马尔可夫决策过程和强化学习
- 3.强化学习训练扩散模型
- 3.1 问题定义
- 3.2 REWARD-WEIGHTED REGRESSION(RWR)
相关文章：
强化学习在文生图中的应用：Training Diffusion Models with Reinforcement Learning
论文链接：Training Diffusion Models with Reinforcement Learning项目地址：Training Diffusion Models with Reinforcement Learning官方代码：https://github.com/kvablack/ddpo-pytorch/tree/maintrl实现：https://huggingface.co/docs/trl/ddpo_trainer🤗关注公众号 fu…...
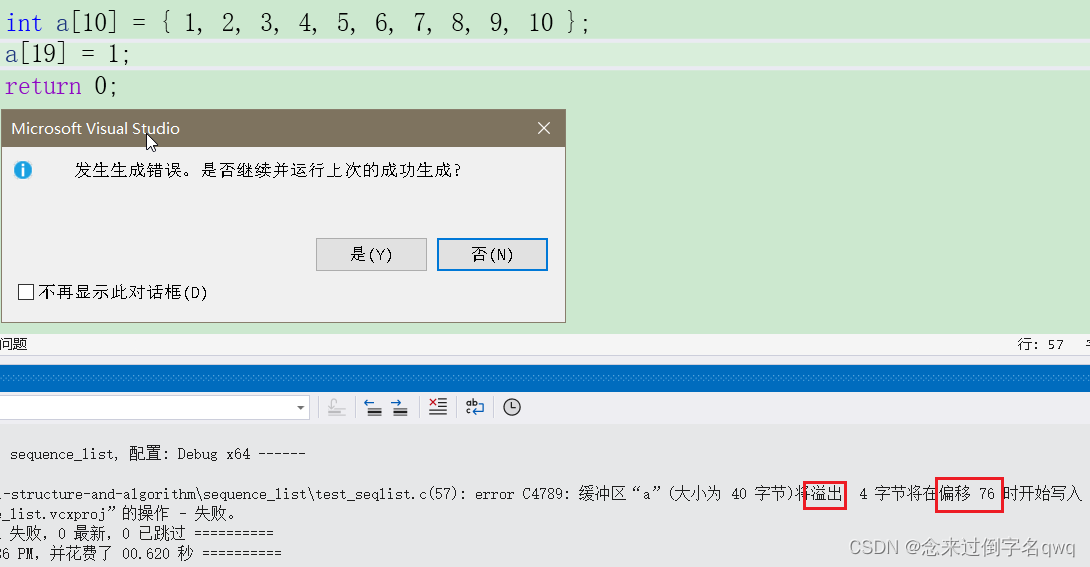
【C语言】数组下标为啥从0开始？下标越界访问一定报错吗？
本篇文章目录 0. 相关文章1. 下标从0开始问题2. 数组下标越界不报错问题 0. 相关文章 指针与指针变量数组名不是首元素地址的的2个例外拨开指针和数组名之间的迷雾 1. 下标从0开始问题 原因是：数组下标访问本质是“指针解引用操作”，而指针又是地址&am…...
机器学习-搜索技术：从技术发展到应用实战的全面指南
在本文中，我们全面探讨了人工智能中搜索技术的发展，从基础算法如DFS和BFS，到高级搜索技术如CSP和优化问题的解决方案，进而探索了机器学习与搜索的融合，最后展望了未来的趋势和挑战，提供了对AI搜索技术深刻的…...
Axelar、J.P.Morgan Onyx、Apollo 完成概念验证，向跨区块链自动化投资领域探索
J.P.Morgan Onyx、Apollo、Axelar、Oasis Pro 以及 Provenance Block Chain 展开合作，共同进行互操作性概念验证（Proof-of-Concept，PoC)。 新加坡 — Axelar Inc.、Oasis Pro 、Provenance Blockchain 与 J.P.Morgan Onyx 以及 Apollo 通过新…...
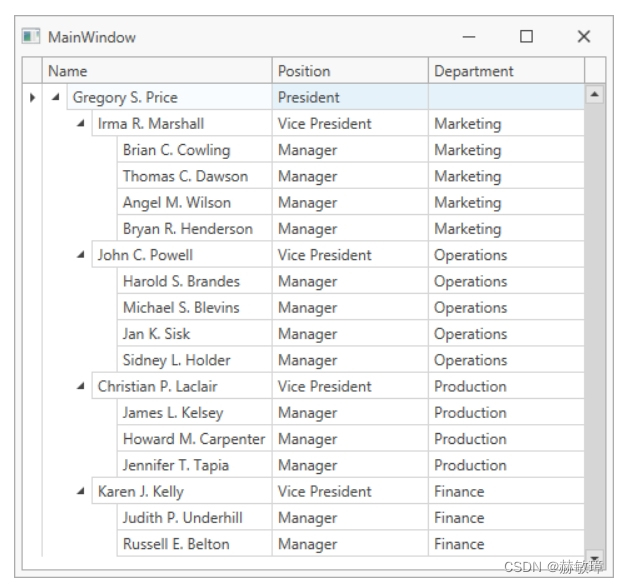
wpf devexpress添加TreeListControl到项目
此教程示范如何添加TreeListControl到项目和绑定控件自引用数据源： 添加数据模型 绑定tree，并添加如下字段到数据源对象： Key字段包含唯一值索引节点 Parent字段包含父索引节点 添加数据模型（Employee和Staff类）到…...
WPF创建自定义控件编译通过但是找不到资源
报错： 原因: 路径写错了： 不是这样： Source"pack://application:,,,/Controls/Styles/xTabControl.xaml" 而是这样： Source"pack://application:,,,/项目名;component/Controls/Styles/xTabControl.xaml …...
PHP 中传值与传引用的区别,什么时候传值什么时候传引用？
传值：当使用传值的方式时，函数或方法会创建原始变量的一个副本，并将该副本传递给函数或方法。在函数或方法内部，对副本的任何修改都不会影响到原始变量。当函数或方法执行完毕后，副本被销毁，不再使用。 传引…...
es安装方式
es安装方式 1.下载镜像的方式 分词器 kibana和es和容器互通的方式 docker network create es-net开始拉去镜像的方式 docker pull kibana:7.12.1运行镜像的方式 docker run -d \--name es \-e "ES_JAVA_OPTS-Xms512m -Xmx512m" \-e "discovery.typesingle-…...
苍穹外卖项目笔记（2）
1 Nginx 反向代理和负载均衡 1.1 概念 【Tips】可以看到前端请求地址和后端接口地址并不匹配，这里涉及到 nginx 反向代理 ，就是将前端发送的动态请求由 nginx 转发到后端服务器 使用 nginx 作反向代理的好处： 提高访问速度（在请…...
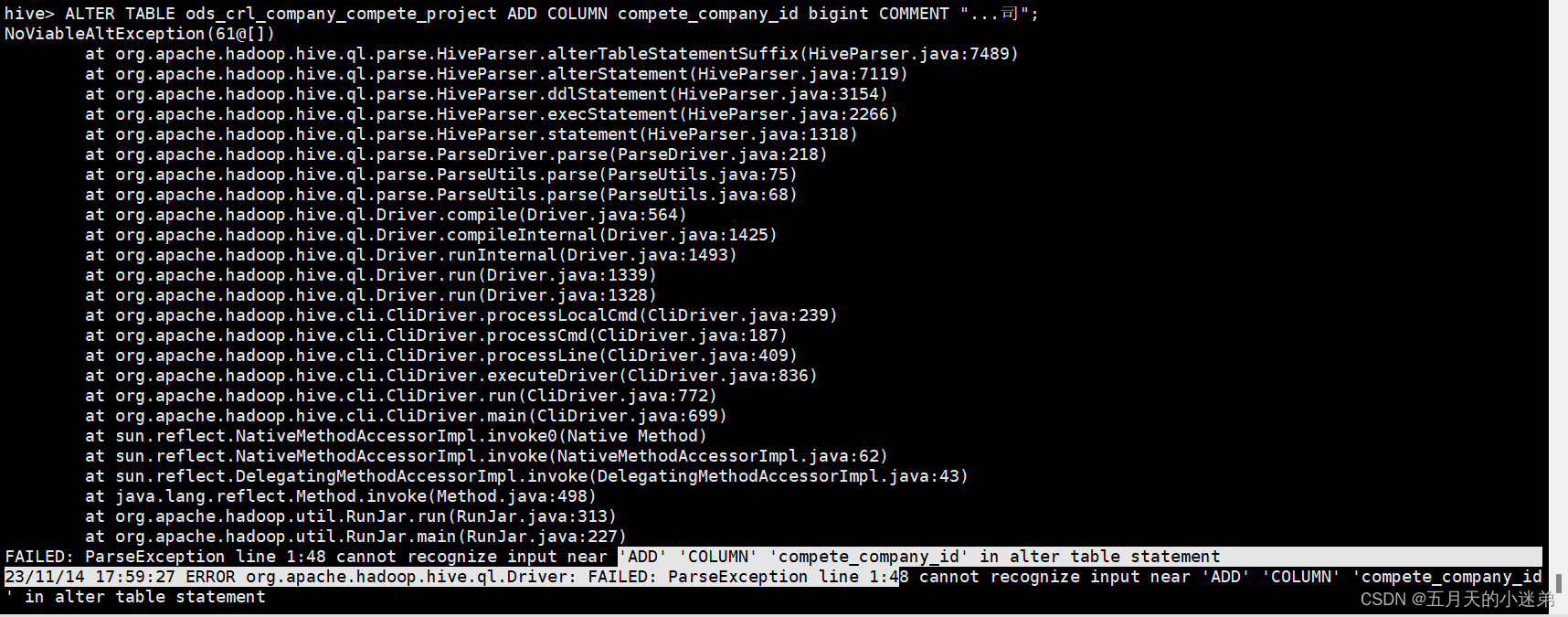
hive更改表结构的时候报错
现象 FAILED: ParseException line 1:48 cannot recognize input near ADD COLUMN compete_company_id in alter table statement 23/11/14 17:59:27 ERROR org.apache.hadoop.hive.ql.Driver: FAILED: ParseException line 1:48 cannot recognize input near ADD COLUMN compe…...
redis运维(六)redis-cli命令
一 redis-cli 注意： redis-cli核redis-server版本必须适配 --> 见 redis-cli --version提示： 不过一般安装服务端 redis-server 时内置了客户端 redis-cli说明： redis-cli 是 redis 的一种命令行的客户端工具备注： redis-se…...
JDK1.8 新特性（二）【Stream 流】
前言 上节我们学了 lambda 表达式，很快我就在 Flink 的学习中用到了，我学的是 Java 版本的 Flink，一开始会以为代码会很复杂，但事实上 Flink 中很多地方都用到了 函数接口，这也让我们在编写 Flink 程序的时候可以使用 …...
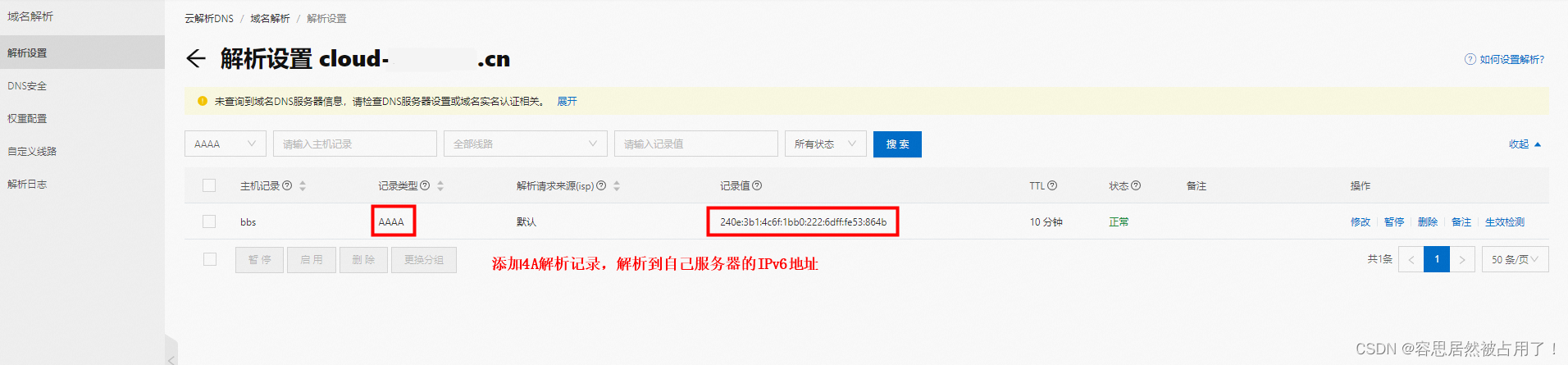
阿里云CentOS主机开启ipv6
目录 一、云主机开启和使用 ipv6 1、网络和交换机开启 ipv6 2、创建 / 编辑云主机，开启ipv6 3、安全组放行ipv6端口 二、使用 ipv6 地址进行 ssh 连接 三、ipv6 地址绑定域名 一、云主机开启和使用 ipv6 1、网络和交换机开启 ipv6 进入网络、交换机详情页面…...
【Git】第五篇：基本操作（添加文件）
.git目录结构 我们在前文中提过了.git目录，也明确说了我们不能手动去.git目录下创建修改等任何操作。 添加文件 我们现在已经了解到，git是一个版本控制器，可以对我们的文件进行管理。而我们需要使用git管理文件的时候，我们必须将…...
vue通过span-method合并列之后，合并列显示在中间位置，根据鼠标滑动跟随展示
当vue通过span-method合并列之后，出现的合并列显示在中间位置，但是如果页面没有分页，如何进行展示呢，难道要滑到最下面去看吗，下面我们来根据鼠标滑动跟随展示 没有处理的合并页面 <template> <el-table:dat…...
gRPC 四模式之 一元RPC模式
一元RPC模式 一元 RPC 模式也被称为简单 RPC 模式。在该模式中，当客户端调用服务器端的远程方法时，客户端发送请求至服务器端并获得一个响应，与响应一起发送的还有状态细节以及 trailer 元数据（这部分不是默认发送的，…...
Java GUI实现贪吃蛇游戏
贪吃蛇是一款经典的游戏，玩法相对简单但富有挑战性。以下是贪吃蛇游戏的基本玩法说明： 目标：控制一条蛇，在游戏区域内吃到尽可能多的食物，使蛇身变长，同时避免撞到自己的身体或游戏区域的边界。 控制&…...
Vue3 使用教程
目录 一、创建vue3工程1. 使用vue-cli创建2.使用 vite 创建 二、setup使用三、ref函数四、reactive函数五、计算属性与监视属性5.1 computed函数5.2 watch函数5.3 watchEffect函数 六、自定义hook函数七、toRef函数八、shallowReactive 与 shallowRef九、readonly 与 shallowRe…...
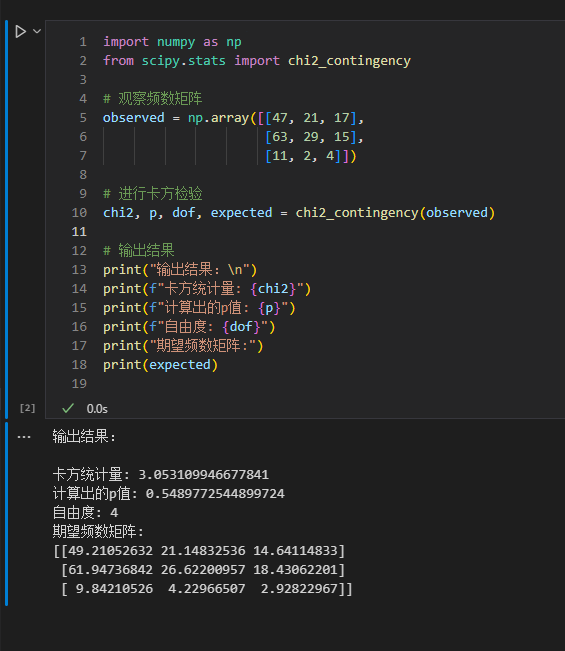
卡方检验-python代码
故事背景 问题 卡方检验的结果怎么计算？ 方法 python代码 import numpy as np from scipy.stats import chi2_contingency# 观察频数矩阵 observed np.array([[47, 21, 17],[63, 29, 15],[11, 2, 4]])# 进行卡方检验 chi2, p, dof, expected chi2_contingency(o…...
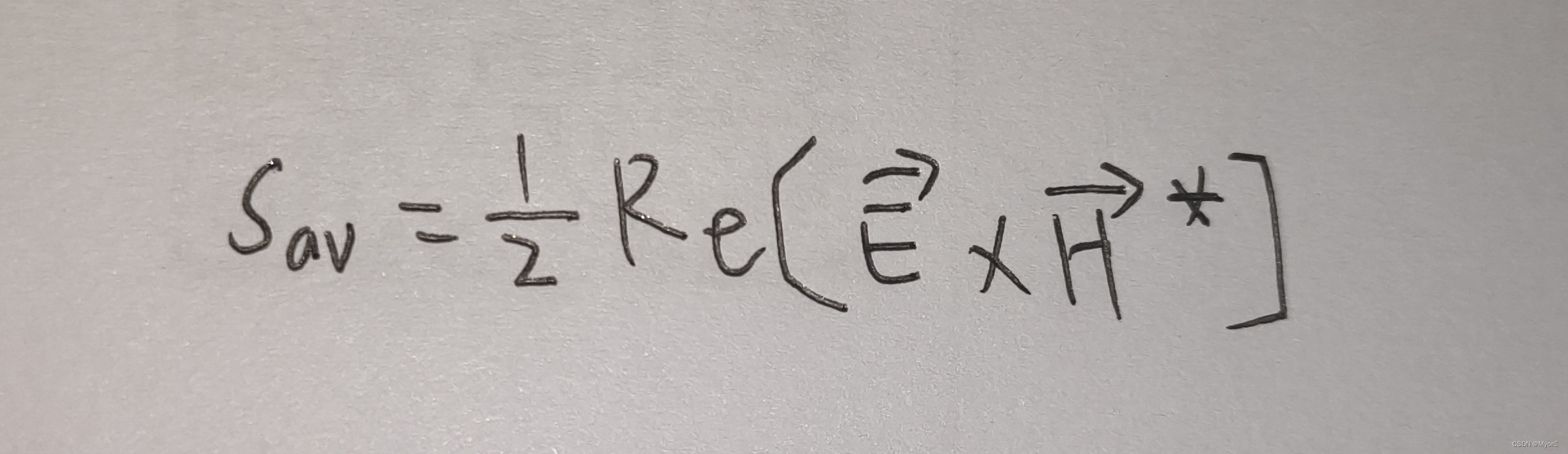
电磁场与电磁波part4--时变电磁场
1、采用洛伦兹条件使得矢量位 与标量位 分离在两个独立的方程中，且矢量位 仅与电流密度 有关，而标量位 仅与电荷密度 有关。 2、电磁能量守恒定理（坡印廷定理） 即减少的电磁能量电磁场所做的功流出的电磁能量 3、设u(r,t)是…...
Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码，写上注释 当然可以！这段代码是 Qt …...
关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径， 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解，但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后，通常在该文件中会出现以下配置&…...
MMaDA: Multimodal Large Diffusion Language Models
CODE ： https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA，它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
高危文件识别的常用算法：原理、应用与企业场景
高危文件识别的常用算法：原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件，如包含恶意代码、敏感数据或欺诈内容的文档，在企业协同办公环境中（如Teams、Google Workspace）尤为重要。结合大模型技术&…...
EtherNet/IP转DeviceNet协议网关详解
一，设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络，本网关连接到EtherNet/IP总线中做为从站使用，连接到DeviceNet总线中做为从站使用。 在自动…...
汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX（不访问内存）XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包： for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
【生成模型】视频生成论文调研
工作清单 上游应用方向：控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
MFC 抛体运动模拟：常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时，我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点，详细解析原因并提供解决方案，同时兼顾界面美化，让模拟效果更专业、更高效。 问题一：历史轨迹与小球残影残留 现象 小球运动后，历史位置的 “残影”…...
Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行： rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...