使用 DFS 轻松求解数独难题(C++ 的一个简单实现)
起因
都说懒惰是第一生产力,最近在玩数独游戏的时候,总会遇到拆解数独比较复杂的情况,就想着自己写个代码解题,解放双手。所以很快就写了一个简单的代码求解经典数独。拿来跑了几个最高难度的数独发现确实很爽!虽说是比较暴力的 DFS,但是由于数独中约束较多的性质,实际上要找出唯一解并不复杂,即使是最高难度的数独也可以在 0.04s 内解完,可以说是非常的方便。
思路
经典数独游戏由 9*9 的方格组成,每个方格可填 1~9 的数字,一般都有三种约束:同行,同列,同宫不可出现相同的数字。只要暴力时利用这些约束,就可以快速剪枝。
考虑最简单的情况:我们对于任何一个空位,可以尝试去填 1~9 的数字,并且检查三种约束是否满足。若满足,就继续填下一个空位。
处理约束
实际上,并不需要每个格子都去把 1~9 全部尝试。因为填的数字越多,约束就越强,我们就越容易发现之前填数时的错误。所以我们可以预先处理三种约束影响的格子范围:
void initializeRelation() {memset(digitsUsed, 0, sizeof digitsUsed);// sub-gridsfor (int i = 0; i < 3; i++) {for (int j = 0; j < 3; j++) {int num = i * 3 + j;for (int k = 0; k < 3; k++) {for (int l = 0; l < 3; l++) {int idx = calcIdx(i * 3 + k, j * 3 + l);group[2][idx] = num;r[num].push_back(idx);}}}}// rowsfor (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {int idx = calcIdx(i, j);group[0][idx] = i + N;r[i + N].push_back(idx);}}// columnsfor (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {int idx = calcIdx(j, i);group[1][idx] = i + N * 2;r[i + N * 2].push_back(idx);}}
}
预先处理完约束后,下次要找一个格子到底应该对应哪些约束时,就可以直接找到对应的 idx 序号了。
状态压缩
一个格子可以填 1~9 共九种数字,那么到底哪些是可以填的呢?就如同我们实际解数独时一样,我们可以在格子上标记一下有哪些数字是符合约束的。一个简单的方法是把这个状态压缩成二进制数,每个可用数字代表一个二进制位的 1,若不可用,则该位为 0。那么一个格子上的可用数字可用一个 9 位二进制数表示,范围是0~2^9,也即一个格子至多只有 512 种状态。
接下来 gcc 有一些方便的内建函数可以帮到我们,它们都是以 __builtin 开头:
__builtin_popcount(unsigned int x)返回无符号整型x的二进制中 1 的个数__builtin_ctz(unsigned int x)返回无符号整型x的二进制的末尾有多少个 0
上述函数也可使用 std::bitset<N>::count 等实现,作用类似。
现在计算某个格子还有多少可用数字就可以这样:
inline int calcUsable(int idx) {return 9 - __builtin_popcount(digitsUsed[idx]);
}
DFS
当我们枚举数字时,其实就是从当前状态中找到下一个可用数字,并根据约束关系删除与其相关的格子中的可用数字。
那么搜索时如何快速判断当前填的数字否可行呢?一个简单的思路是每次找到可用数字最少的格子,这样的格子可以确定更多的约束,搜索空间也更少,一旦失败了,我们可以迅速回滚。
那么把所有的空格子按照他们的[可用数字个数,可用数字状态]作为一个数对,我们就可以利用std::set构造出一个暴力 DFS 方案:
bool dfs() {if (grid.empty()) {return true;}pair<int, int> p = *grid.begin();grid.erase(p);int idx = p.second;int digitBit = MASK & ~digitsUsed[idx];for (int nextDigitBit = digitBit; nextDigitBit; nextDigitBit ^= lowbit(nextDigitBit)) {int digit = lowbit0Count(nextDigitBit);int currentDigitBit = 1 << digit;g[idx] = digit + 1;vector<int> last;for (int j = 0; j < 3; j++) {for (auto & x: r[group[j][idx]]) {auto it = grid.find(make_pair(calcUsable(x), x));if (it != grid.end() && (digitsUsed[x] | currentDigitBit) != digitsUsed[x]) {grid.erase(it);digitsUsed[x] = digitsUsed[x] | currentDigitBit;grid.insert(make_pair(calcUsable(x), x));last.push_back(x);}}}if (dfs()) {return true;}for (auto &x: last) {grid.erase(make_pair(calcUsable(x), x));digitsUsed[x] = digitsUsed[x] & ~currentDigitBit;grid.insert(make_pair(calcUsable(x), x));}}grid.insert(p);return false;
}
结语
由于只考虑经典数独,代码还是非常简洁而且高效的。而对于各种各样的变形数独,也可以考虑根据这种简化约束的方式去暴力求解。如果想要模仿人类解法,对强弱链等逻辑进行推演而非简单暴力的话,还需要更多的工作。
当然,数独如果由机器暴力计算就会缺失很多乐趣,但去寻找现有问题的一种代码实现也同样是另一种乐趣。我觉得能在数学游戏中找到自己喜欢的部分,并发掘出其中的趣味,其本身也是一种快乐的事情。
附录
最终代码如下,输入重定向于sudoku.in,输入格式中星号*代表空位,可在代码最后注释中看到样例。
输出格式为先输出整体的解,再输出只包含原数独中空位的解。
#include <bits/stdc++.h>using namespace std;const int N = 9;
const int R_NUM = 27;
const int GRID_NUM = 81;
const int MASK = (1 << N) - 1;char str[10][100];
int s[9][9];
int g[GRID_NUM];
int group[3][GRID_NUM]; // groups
vector<int> r[R_NUM]; // relations
set<pair<int, int>> grid;
int digitsUsed[GRID_NUM];/**
group 0:
000000000
111111111
222222222
333333333
444444444
555555555
666666666
777777777
888888888group 1:
012345678
012345678
012345678
012345678
012345678
012345678
012345678
012345678
012345678group 2:
000111222
000111222
000111222
333444555
333444555
333444555
666777888
666777888
666777888
**/inline int calcX(int idx) {return group[0][idx];
}inline int calcIdx(int x, int y) {return x * N + y;
}inline int lowbit(int x) {return x & (-x);
}inline int lowbit0Count(int x) {return __builtin_ctz(x);
}inline int calcUsable(int idx) {return 9 - __builtin_popcount(digitsUsed[idx]);
}void initializeRelation() {memset(digitsUsed, 0, sizeof digitsUsed);// sub-gridsfor (int i = 0; i < 3; i++) {for (int j = 0; j < 3; j++) {int num = i * 3 + j;for (int k = 0; k < 3; k++) {for (int l = 0; l < 3; l++) {int idx = calcIdx(i * 3 + k, j * 3 + l);group[2][idx] = num;r[num].push_back(idx);}}}}// rowsfor (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {int idx = calcIdx(i, j);group[0][idx] = i + N;r[i + N].push_back(idx);}}// columnsfor (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {int idx = calcIdx(j, i);group[1][idx] = i + N * 2;r[i + N * 2].push_back(idx);}}
}void fail() {printf("IMPOSSIBLE\n");exit(0);
}void printResult() {printf("Result:\n");for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {printf("%d", g[calcIdx(i, j)]);}printf("\n");}
}void printFillableResult() {printf("\nFillable Result:\n");for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {printf("%c", (s[i][j] == 0) ? g[calcIdx(i, j)] + '0' : '*');}printf("\n");}
}bool dfs() {if (grid.empty()) {return true;}pair<int, int> p = *grid.begin();grid.erase(p);int idx = p.second;int digitBit = MASK & ~digitsUsed[idx];for (int nextDigitBit = digitBit; nextDigitBit; nextDigitBit ^= lowbit(nextDigitBit)) {int digit = lowbit0Count(nextDigitBit);int currentDigitBit = 1 << digit;g[idx] = digit + 1;vector<int> last;for (int j = 0; j < 3; j++) {for (auto & x: r[group[j][idx]]) {auto it = grid.find(make_pair(calcUsable(x), x));if (it != grid.end() && (digitsUsed[x] | currentDigitBit) != digitsUsed[x]) {grid.erase(it);digitsUsed[x] = digitsUsed[x] | currentDigitBit;grid.insert(make_pair(calcUsable(x), x));last.push_back(x);}}}if (dfs()) {return true;}for (auto &x: last) {grid.erase(make_pair(calcUsable(x), x));digitsUsed[x] = digitsUsed[x] & ~currentDigitBit;grid.insert(make_pair(calcUsable(x), x));}}grid.insert(p);return false;
}int main() {freopen("sudoku.in", "r", stdin);initializeRelation();// Enter a sudoku puzzle: (9 lines with 9 characters on each line, use * for blank)for (int i = 0; i < N; i++) {scanf("%s", str[i]);}for (int i = 0; i < N; i++) {if (strlen(str[i]) != N) {exit(0);}for (int j = 0; j < N; j++) {int idx = calcIdx(i, j);if (str[i][j] == '*') {g[idx] = s[i][j] = 0;digitsUsed[idx] = 0;} else if (str[i][j] >= '1' && str[i][j] <= '9') {g[idx] = s[i][j] = str[i][j] - '0';} else {exit(0);}}}for (int idx = 0; idx < GRID_NUM; idx++) {if (g[idx] == 0) {for (int j = 0; j < 3; j++) {for (auto & cur: r[group[j][idx]]) {if (g[cur] != 0) {digitsUsed[idx] |= 1 << (g[cur] - 1);}}}// pair is (digitsLeftCount, idx)grid.insert(make_pair(calcUsable(idx), idx));}}if (dfs()) {printResult();printFillableResult();} else {printResult();fail();}return 0;
}/*
<Sample Input>*23456789
456789123
789123456
312645978
645978312
978312645
231564897
564897231
897231564**95*8*7*
23769***4
5**32**1*
8*1935**7
49*8*2*51
**3**6*2*
*1*2*4**6
6*8*****2
*7*1*38*******2***
2*4****7*
****5**49
**6**85**
******83*
57**4****
*3*7****6
*65*3**9*
7***9*1***/
相关文章:
)
使用 DFS 轻松求解数独难题(C++ 的一个简单实现)
起因 都说懒惰是第一生产力,最近在玩数独游戏的时候,总会遇到拆解数独比较复杂的情况,就想着自己写个代码解题,解放双手。所以很快就写了一个简单的代码求解经典数独。拿来跑了几个最高难度的数独发现确实很爽!虽说是…...
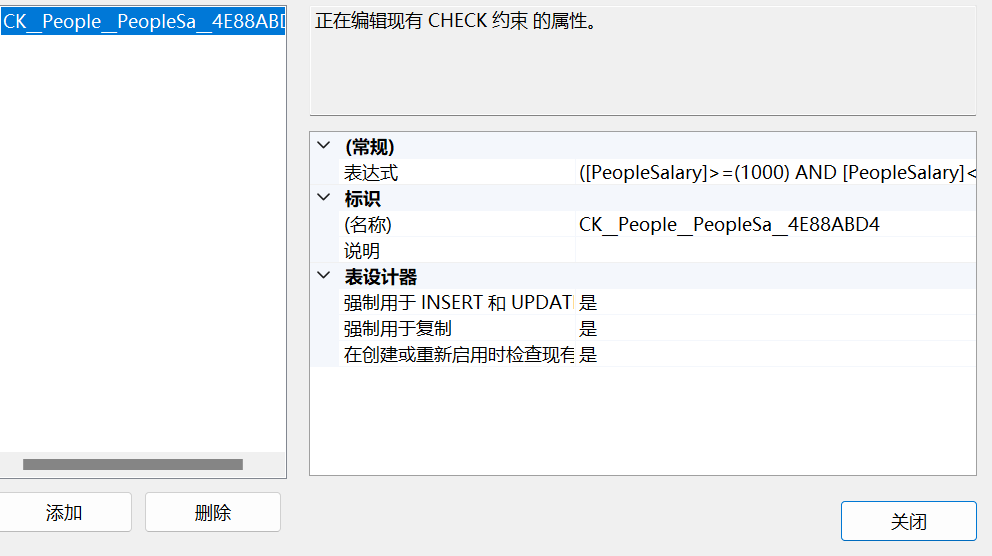
【SQL server】 表结构的约束和维护
表结构的约束和维护 修改表结构 (1)添加列 (2)删除列 (3)修改列alter table 表名 add 新列名 数据类型给员工表添加一列邮箱 alter table People add PeopleMail varchar(200)删除列 alter table People drop column PeopleMain修改列 alter table 表名 alter column 列名 数据…...

竞赛 题目:基于大数据的用户画像分析系统 数据分析 开题
文章目录 1 前言2 用户画像分析概述2.1 用户画像构建的相关技术2.2 标签体系2.3 标签优先级 3 实站 - 百货商场用户画像描述与价值分析3.1 数据格式3.2 数据预处理3.3 会员年龄构成3.4 订单占比 消费画像3.5 季度偏好画像3.6 会员用户画像与特征3.6.1 构建会员用户业务特征标签…...

Vue3-ref、reactive函数的watch
Vue3-ref、reactive函数的watch ref函数的watch 原理:监视某个属性的变化。当被监视的属性一旦发生改变时,执行某段代码。watch 属性中的数据需要具有响应式watch 属性可以使用箭头函数watch 属性可以监视一个或者多个响应式数据,并且可以配…...

【智能家居项目】FreeRTOS版本——多任务系统中使用DHT11 | 获取SNTP服务器时间 | 重新设计功能框架
🐱作者:一只大喵咪1201 🐱专栏:《智能家居项目》 🔥格言:你只管努力,剩下的交给时间! 目录 🍓多任务系统中使用DHT11🍅关闭调度器🍅使用中断 &am…...
鸿蒙APP外包开发需要注意的问题
在进行鸿蒙(HarmonyOS)应用开发时,开发者需要注意一些重要的问题,以确保应用的质量、性能和用户体验。以下是一些鸿蒙APP开发中需要特别关注的问题,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软…...

Redis 19 事务
Redis通过MULTI、EXEC、WATCH等命令来实现事务(transaction)功能。事务提供了一种将多个命令请求打包,然后一次性、按顺序地执行多个命令的机制,并且在事务执行期间,服务器不会中断事务而改去执行其他客户端的命令请求…...

Fabric多机部署启动节点与合约部署
这是我搭建的fabric的网络拓扑 3 个 orderer 节点;组织 org1 , org1 下有两个 peer 节点, peer0 和 peer1; 组织 org2 , org2 下有两个 peer 节点, peer0 和 peer1; 以上是我的多机环境的网络拓扑,使用的是docker搭建的。我的网络…...
WordPress主题WoodMart v7.3.2 WooCommerce主题和谐汉化版下载
WordPress主题WoodMart v7.3.2 WooCommerce主题和谐汉化版下载 WoodMart是一款出色的WooCommerce商店主题,它不仅提供强大的电子商务功能,还与流行的Elementor页面编辑器插件完美兼容。 主题文件在WoodMart Theme/woodmart.7.3.2.zip,核心在P…...

Java 高等院校分析与推荐系统
1)项目简介 随着我国高等教育的大众化,高校毕业生就业碰到了前所未有的压力,高校学生就业问题开始进入相关研究者们的视野。在高校学生供给忽然急剧增加的同时,我国高校大学生的就业机制也在发生着深刻的变化,作为就业…...

【JVM】Java虚拟机
本文主要介绍了JVM的内存区域划分,类加载机制以及垃圾回收机制. 其实JVM的初心,就是让java程序员不需要去了解JVM的细节,它把很多工作内部封装好了.但是学习JVM的内部原理有利于我们深入理解学习Java. 1.JVM的内存区域划分 JVM其实是一个java进程 ; 每个java进程,就是一个jvm…...
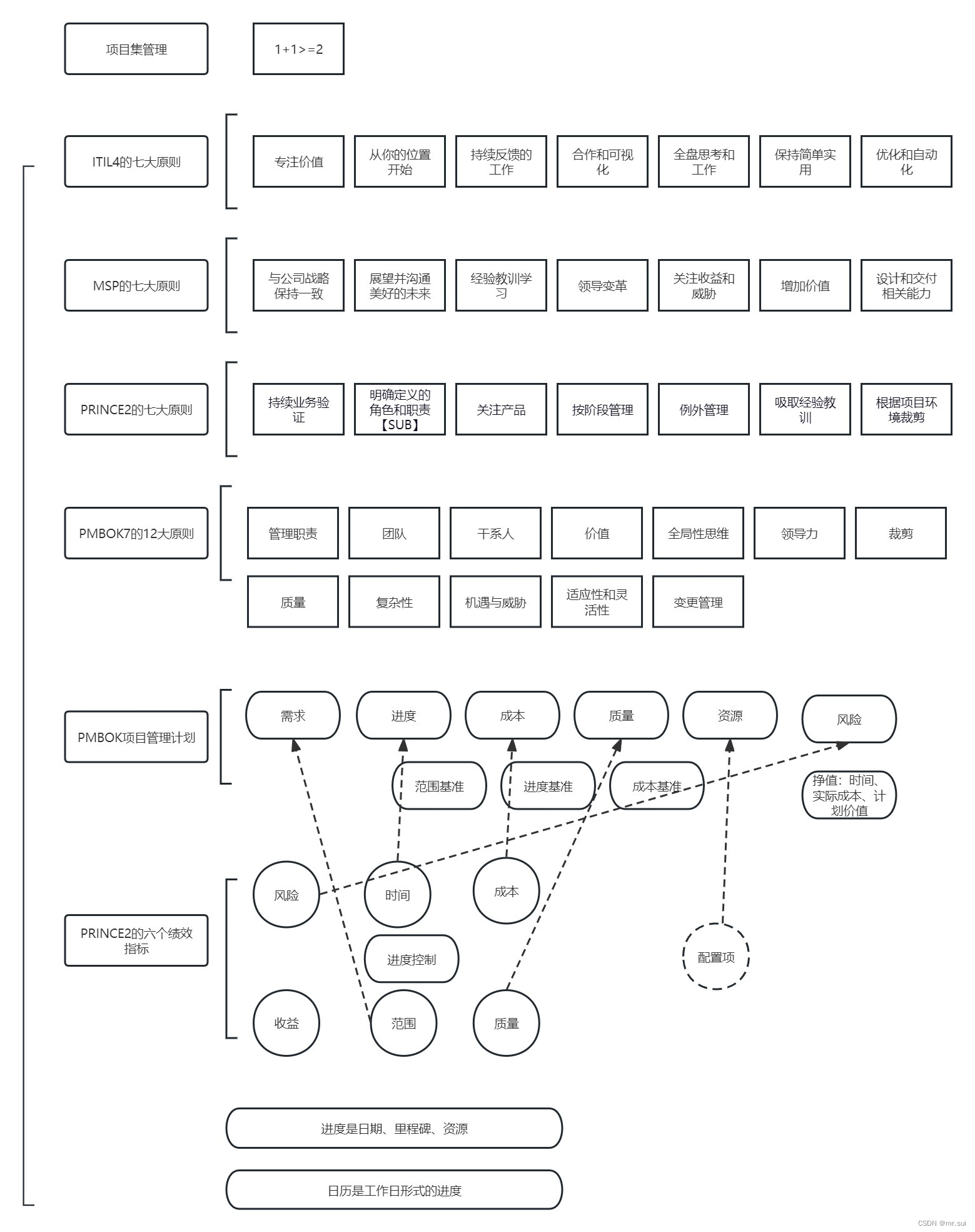
业务架构、技术架构、项目管理的有机结合
新入职的创业公司一年不行了。 这一年来没有上班,也因为大龄的问题找不到合适的工作。然后考了几个项目管理证书,又思考了一个技术兑现的问题。 技术本身是架构的执行层面,如果上面的公司战略、业务架构变小,缩水,或者…...

拜耳阵列(Bayer Pattern)以及常见彩色滤波矩阵(CFA)
一、拜耳阵列的来源 图像传感器将光线转化成电流,光线越亮,电流的数值就越大;光线越暗,电流的数值就越小。图像传感器只能感受光的强弱,无法感受光的波长。由于光的颜色由波长决定,所以图像传播器无法记录…...

【信息安全】浅谈IDOR越权漏洞的原理、危害和防范:直接对象引用导致的越权行为
前言 ┌──────────────────────────────────┐ │ 正在播放《越权访问》 - Hanser │ ●━━━━━━─────── 00:00 / 03:05 │ ↻ ◁ ❚❚ ▷ ⇆ └───────────────────────────────…...

uni-app 蓝牙打印, CPCL指令集使用
先上代码: GitHub - byc233518/uniapp-bluetooth-printer-demo: 使用uniApp 连接蓝牙打印机 Demo, CPCL 指令简单实用示例 (内含 芝珂,佳博,精臣 多个厂家指令集使用文档) 文件结构: ├── App.vue ├── CPCL 指令手册.pdf // 指令集参考手册 ├── LICENSE ├── R…...

vue-组件通信(二)
🌈个人主页:前端青山 🔥系列专栏:Vue篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来vue篇专栏内容:vue-组件通信(二) 目录 组件通信(二) (1) props / $emit 1. 父组件向子组…...
2023年【危险化学品经营单位安全管理人员】考试题及危险化学品经营单位安全管理人员模拟试题
题库来源:安全生产模拟考试一点通公众号小程序 危险化学品经营单位安全管理人员考试题是安全生产模拟考试一点通总题库中生成的一套危险化学品经营单位安全管理人员模拟试题,安全生产模拟考试一点通上危险化学品经营单位安全管理人员作业手机同步练习。…...

Uni-App常用事件
Uni-App是一个跨平台的前端开发框架,支持多个平台的应用开发,包括H5、小程序、App等。在Uni-App中,有许多常用的事件可以用来处理用户交互、页面生命周期等方面的逻辑。以下是一些Uni-App中常用的事件: 点击事件(click…...

【笔记 Pytorch】稀疏矩阵、scipy.sparse模块的使用
安装:pip install scipy 描述:就是专门为了解决稀疏矩阵而生。导入模块:from scipy import sparse 优缺点总结 七种矩阵类型描述coo_matrix ★【名称】coordinate format 【优点】 ① 不同稀疏格式间转换效率高(特别是CSR和CSC) …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

