选硬币该用动态规划
选硬币:
现有面值分别为1角1分,5分,1分的硬币,请给出找1角5分钱的最佳方案。
#include <iostream>
#include <vector>std::vector<int> findChange(int amount) {std::vector<int> coins = {11, 5, 1}; // 按面值从大到小排序的硬币面值std::vector<int> result(coins.size(), 0); // 用于存储每种硬币的数量for (int i = 0; i < coins.size(); i++) {int numCoins = amount / coins[i]; // 计算当前硬币面值的数量result[i] = numCoins; // 存储数量amount -= numCoins * coins[i]; // 更新剩余金额}return result;
}int main() {int amount = 15; // 需要找零的金额,单位为分std::vector<int> change = findChange(amount);std::cout << "找零方案为:" << std::endl;std::cout << "1角1分硬币数量:" << change[0] << std::endl;std::cout << "5分硬币数量:" << change[1] << std::endl;std::cout << "1分硬币数量:" << change[2] << std::endl;return 0;
}
一开始我想的很简单,以为是简单的求整除数。
但要是你仔细一想,这肯定是不对的,不是所有问题都能用贪心。
在求最优的过程中,贪心和动态规划一直是一对冤家,到底选择哪个,难道了很多英雄好汉,所以最好的方式就是具体问题具体分析,只有结合实际情况才能选出最适合问题的算法。
我们都知道贪心的局限性,只能求出其中一个解的,但是不是最优需要考量。
让我们来看一下用上面贪心求出来的解:

但这肯定不是最优解,我们在找零的时候遵循的规则是用最少的钱张数交给别人,这样才方便。
所以最佳找零方案为:
1角1分硬币数量:0
5分硬币数量:3
1分硬币数量:0
让我们来看看用动态规划写出来的代码:
#include <iostream>
using namespace std;const int N = 10005;
const int INF = 0x3f3f3f3f;
int f[N], a[N];int main() {int n, w;cin >> n >> w;for (int i = 0; i < n; i++) {cin >> a[i];}for (int i = 1; i <= w; i++) {f[i] = INF;}for (int i = 0; i < n; i++) {for (int j = a[i]; j <= w; j++) {f[j] = min(f[j], f[j - a[i]] + 1);}}if (f[w] == INF) {cout << -1; } else {cout << f[w];}return 0;
}

结果和我们预期的完全一样
总结
选硬币在动态规划中是一种叫状态表示的题型,通常用一维/二维的数组组成状态转移方程,通过更新数组来达到获取最优解的目标
相关文章:

选硬币该用动态规划
选硬币: 现有面值分别为1角1分,5分,1分的硬币,请给出找1角5分钱的最佳方案。 #include <iostream> #include <vector>std::vector<int> findChange(int amount) {std::vector<int> coins {11, 5, 1}; /…...

LeetCode 2342. 数位和相等数对的最大和:哈希表
【LetMeFly】2342.数位和相等数对的最大和:哈希表 力扣题目链接:https://leetcode.cn/problems/max-sum-of-a-pair-with-equal-sum-of-digits/ 给你一个下标从 0 开始的数组 nums ,数组中的元素都是 正 整数。请你选出两个下标 i 和 j&…...
Vulkan渲染引擎开发教程 一、开发环境搭建
一 安装 Vulkan SDK Vulkan SDK 就是我们要搞的图形接口 首先到官网下载SDK并安装 https://vulkan.lunarg.com/sdk/home 二 安装 GLFW 窗口库 GLFW是个跨平台的小型窗口库,也就是显示窗口,图形的载体 去主页下载并安装,https://www.glfw.…...
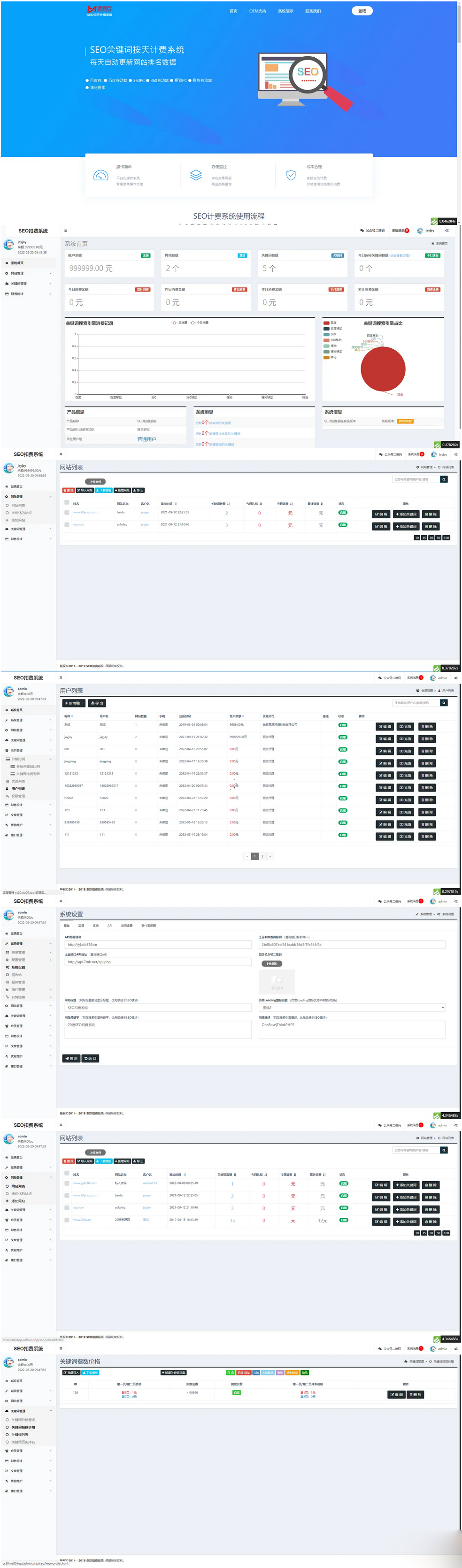
(带教程)商业版SEO关键词按天计费系统:关键词排名优化、代理服务、手机自适应及搭建教程
源码简介: 1、会员管理: 该系统分为三个级别的会员流程:总站管理员、代理与会员(会员有普通会员、中级会员和高级会员三个等级)。总站管理员可以添加代理用户并为其充值余额,代理用户可以为普通用户充值余…...
IDEA 快捷键汇总
目录 1、altinsert 2、ctrl/ 3、altenter 4、alt回车 5、ctrlD 6、ctrlaltL 7、ctrl点击 8、alt左键向下拉 9、ctrlaltv 10、ctrlaltwint 1、altinsert 快速创建代码,可以快速创建类中get set tostring等方法 2、ctrl/ 单行注释 3、altenter…...

目标检测YOLO实战应用案例100讲-基于机器视觉的水稻病虫害监测预警
目录 前言 国内外研究现状 国外研究现状 国内研究现状 2 相关理论与技术...

OrthoNets:正交信道注意网络
文章目录 摘要1、简介2、相关工作3、方法4、实验设置及结果5、论述6、结论摘要 链接:https://arxiv.org/pdf/2311.03071v2.pdf 设计有效的通道注意力机制要求人们找到一种有损压缩方法,以实现最佳特征表示。尽管该领域近年来取得了进展,但仍然存在一个未解决的问题。FcaNet…...
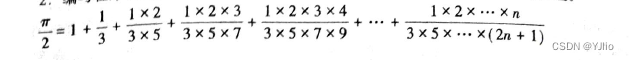
C_12练习题
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) C 风格的注释,也称块注释或多行注释,以()…...

导航守卫有哪三种?
导航守卫主要分为三种: 全局前置守卫:使用 router.beforeEach 注册,作用是在路由切换开始前进行拦截和处理,可以用来进行一些全局的权限校验、登录状态检查等操作。 全局解析守卫:使用 beforeResolve 注册,…...

强烈 推荐 13 个 Web前端在线代码IDE
codesandbox.io(国外,提供免费空间) 网址:https://codesandbox.io/ CodeSandbox 专注于构建完整的 Web 应用程序,支持多种流行的前端框架和库,例如 React、Vue 和 Angular。它提供了一系列增强的功能&…...

网络协议 WebSocket
一、介绍 WebSocket 是基于 TCP 的一种新的网络协议。它实现了浏览器与服务器全双工通信——浏览器和服务器只需要完成一次握手,两者之间就可以创建持久性的连接, 并进行双向数据传输 1、HTTP协议和WebSocket协议对比 HTTP 是短连接WebSocket 是长连接H…...

路径操作 合法路径名
python中路径的三种合法表示:在路径前面加上r、分隔符使用/。 在路径前面加上r python中在前面加上r,是防止字符转义。 例如:这样一个路径: \Undergraduate\School\Programme\Python_Learnpython会将这个字符串的**\和\后面的…...

JavaEE初阶 01 计算机是如何工作的
前言 今天开始进行对JavaEE的一些基本总结,希望大家能在阅读中有所收获,如有错误还望多多指正. 1.冯诺依曼体系结构 这个体系结构相信学计算机的同学都不陌生,但是你真的知道这个体系结构说的是什么嘛?请听我娓娓道来.首先我先给出一张冯诺依曼体系结构的简图 你可以理解为当前…...

【shell 常用脚本30例】
先了解下编写Shell过程中注意事项 开头加解释器:#!/bin/bash语法缩进,使用四个空格;多加注释说明。命名建议规则:全局变量名大写、局部变量小写,函数名小写,名字体现出实际作用。默认变量是全局的…...

【我和Python算法的初相遇】——体验递归的可视化篇
🌈个人主页: Aileen_0v0 🔥系列专栏:PYTHON数据结构与算法学习系列专栏💫"没有罗马,那就自己创造罗马~" 目录 递归的起源 什么是递归? 利用递归解决列表求和问题 递归三定律 递归应用-整数转换为任意进制数 递归可视化 画…...
【C语言的秘密】密探—深究C语言中多组输入的秘密!
场景引入: 你是否在刷题过程中,经常遇到以下场景呢? 场景一: 场景二: 从这些题上都能看见输入描述中提出了一条多组输入,那啥是多组输入?如何实现它呢? 多组输入:在输入…...

ClickHouse 语法优化规则
ClickHouse 的 SQL 优化规则是基于RBO(Rule Based Optimization),下面是一些优化规则 1 准备测试用表 1)上传官方的数据集 将visits_v1.tar和hits_v1.tar上传到虚拟机,解压到clickhouse数据路径下 // 解压到clickhouse数据路径 sudo tar -xvf…...

3-运行第一个docker image-hello world
CentOS7.9下安装完成docker后,我们开始部署第一个docker image-hello world 1.以root用户登录CentOS7.9服务器,拉取centos7 images 命令: docker pull hello-world [root@centos79 ~]# docker pull hello-world Using default tag: latest latest: Pulling from library…...
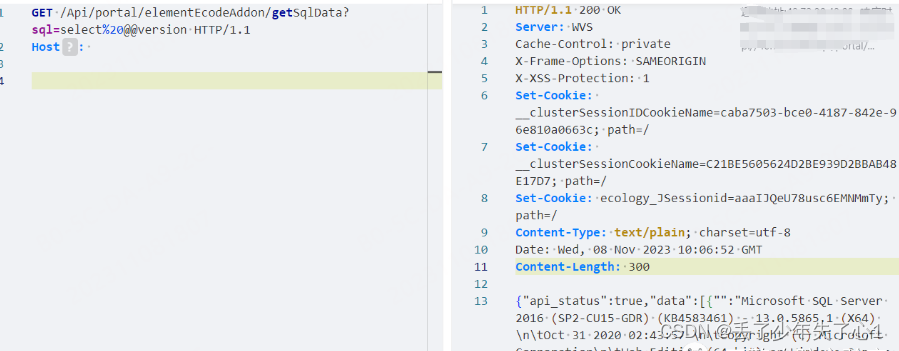
【漏洞复现】泛微e-Weaver SQL注入
漏洞描述 泛微e-Weaver(FANWEI e-Weaver)是一款广泛应用于企业数字化转型领域的集成协同管理平台。作为中国知名的企业级软件解决方案提供商,泛微软件(广州)股份有限公司开发和推广了e-Weaver平台。 泛微e-Weaver旨在…...
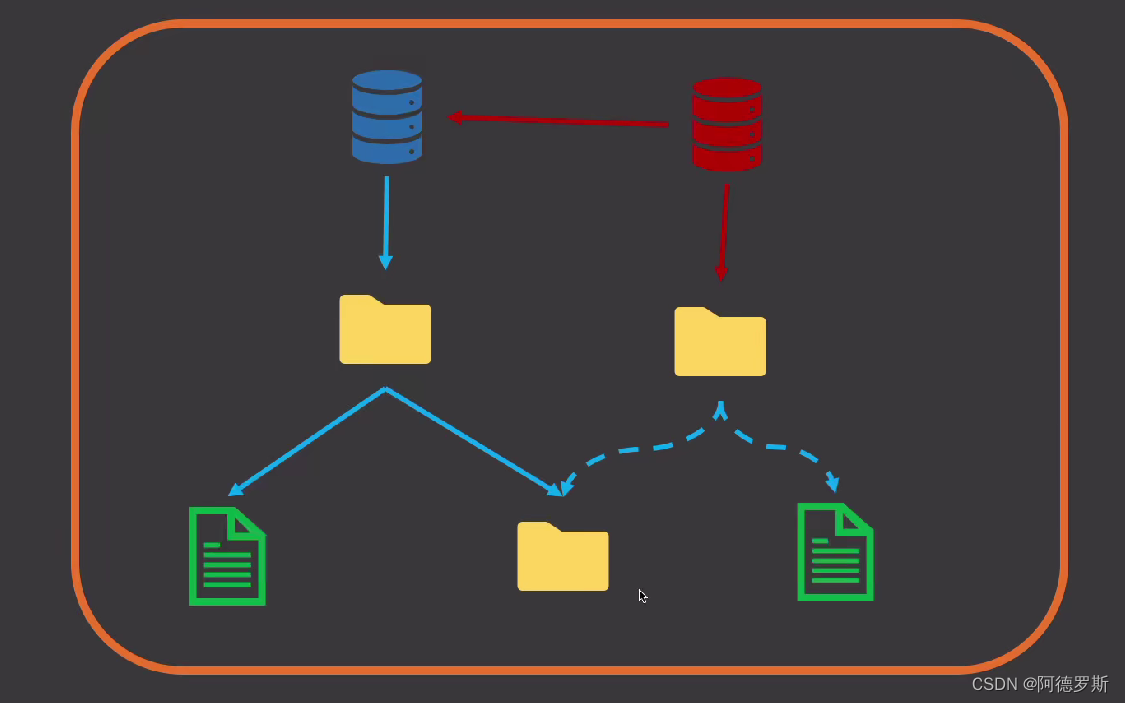
「git 系列」git 如何存储代码的?
这里写自定义目录标题 git 文件存储位置git 数据模型示例分析分析前准备命令哈希值 具体示例 不同版本的提交,git 做了什么工作?snapshot vs delta-based vs backup参考资料 git 文件存储位置 想要了解如何存储,首先需要知道存储位置。 当我…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
