数据结构02附录01:顺序表考研习题[C++]

图源:文心一言
考研笔记整理~🥝🥝
之前的博文链接在此:数据结构02:线性表[顺序表+链表]_线性链表-CSDN博客~🥝🥝
本篇作为线性表的代码补充,每道题提供了优解和暴力解算法,供小伙伴们参考~🥝🥝
- 第1版:无情地Push Chat GPT老师写代码、分析GPT老师写的代码并思考弱智解~🧩🧩
编辑:梅头脑🌸
参考用书:王道考研《2024年 数据结构考研复习指导》
📇目录
📇目录
🧵2010统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
⌨️优解演算
🌰暴力解
📇暴力解思路
⌨️暴力解代码
⌨️暴力解演算
🧵2011统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
⌨️优解演算
🌰暴力解
📇暴力解思路
⌨️暴力解代码
⌨️暴力解演算
🧵2013统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
⌨️优解演算
🌰暴力解
📇暴力解思路
⌨️暴力解代码
⌨️暴力解演算
🧵2018统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
🧵2020统考真题
🧩题目
🌰优解
📇优解思路
⌨️优解代码
🌰暴力解
📇暴力解思路
⌨️暴力解代码
🔚结语
🧵2010统考真题
🧩题目
设将n个整数存放到一维数组R中。设计一个在时间和空间两方面都尽可能高效的算法。将R中保存的序列循环左移p个位置,即将R的数据由(X0,X1,…,Xn-1)变换为(Xp,Xp+1,…Xn-1,X0,X1,…,Xp-1)。
🌰优解
📇优解思路
- 算法思想:
- 将数组p(n-p)转化为数组(n-p)p,(n-p)p=(p-1(n-p)-1)-1;
- 因此分别反转前p项,后n-p项,最后整体反转p-1(n-p)-1;
- reverse函数用于反转数组中指定范围的元素,它通过交换两端的元素来实现反转。
- 时间复杂度:O(n),其中n是数组的长度,因为需要反转数组的两部分和整体数组。
- 空间复杂度:O(1),因为算法只使用了固定的额外空间来存储一些临时变量,与数组的长度无关。
⌨️优解代码
#include <iostream>
using namespace std;// 反转数组中指定范围的元素
void reverse(int arr[], int start, int end) {// 使用双指针法将数组中指定范围的元素进行反转// start 指向要反转的范围的起始位置,end 指向要反转的范围的末尾位置while (start < end) {// 交换 start 和 end 位置的元素int temp = arr[start];arr[start] = arr[end];arr[end] = temp;// 向中间移动双指针start++;end--;}
}// 执行循环左移操作
void rotateLeft(int arr[], int n, int p) {// 将左移位数取模以确保它在数组长度范围内p = p % n;if (p == 0) return; // 如果左移位数为0,直接返回,不需要进行操作reverse(arr, 0, p - 1); // 反转前半部分reverse(arr, p, n - 1); // 反转后半部分reverse(arr, 0, n - 1); // 整体反转
}int main() {const int n = 10; // 数组长度为10const int p = 3; // 左移3位int arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; // 初始化数组元素rotateLeft(arr, n, p); // 执行左移操作// 输出结果cout << "左移后的数组为: ";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}return 0;
}
⌨️优解演算
- 初始轮 arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; temp = NULL;
- 第一轮 arr[n] = {2, 1, 0, 3, 4, 5, 6, 7, 8, 9}; temp = 0;
- 第二轮 arr[n] = {2, 1, 0, 9, 8, 7, 6, 5, 4, 3}; temp = 3;temp = 4;temp = 5;
- 第三轮 arr[n] = {3, 4, 5, 6, 7, 8, 9, 0, 1, 2}; temp = 2;temp = 1;temp = 0;temp = 9;temp = 8;
🌰暴力解
📇暴力解思路
- 算法思想:
- 创建一个临时数组 temp,用于存储前p个元素。
- 将后面的元素向前移动p个位置,留出前p个位置用于粘贴临时数组的内容。
- 将临时数组中的元素复制回原数组的末尾。
- 时间复杂度:O(n),因为我们额外使用了一个临时数组 temp 来存储前p个元素。这个临时数组的大小与左移的位数p相等,因此空间复杂度是O(p),而在最坏情况下,p可以等于n,所以空间复杂度可以达到O(n)。
- 空间复杂度:O(n),理由同上。
⌨️暴力解代码
#include <iostream>
using namespace std;void rotateLeft(int arr[], int n, int p) {int temp[p]; // 创建一个临时数组用于存储前p个元素// 复制前p个元素到临时数组中for (int i = 0; i < p; i++) {temp[i] = arr[i];}// 将后面的元素向前移动p个位置for (int i = p; i < n; i++) {arr[i - p] = arr[i];}// 将临时数组中的元素复制回原数组末尾for (int i = 0; i < p; i++) {arr[n - p + i] = temp[i];}
}int main() {const int n = 10; // 数组长度为10const int p = 3; // 左移3位int arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; // 初始化数组元素rotateLeft(arr, n, p); // 执行左移操作// 输出结果cout << "左移后的数组为: ";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}return 0;
}
⌨️暴力解演算
- 初始轮 arr[n] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; temp[p] = NULL;
- 第一轮 arr[n] = {2, 1, 0, 3, 4, 5, 6, 7, 8, 9}; temp[p] = {2, 1, 0};
- 第二轮 arr[n] = {3, 4, 5, 6, 7, 8, 9, 7, 8, 9}; temp[p] = {2, 1, 0};
- 第三轮 arr[n] = {3, 4, 5, 6, 7, 8, 9, 0, 1, 2}; temp[p] = {2, 1, 0};
🧵2011统考真题
🧩题目
一个长度为L的升序序列S,处在第[L/2]个位置的元素称为S的中位数。例如,若序列S1=(11,13,15,17,19),则S1的中位数是15,两个序列的中位数是他们所有元素的升序序列的中位数。例如若S2=(2,4,6,8,10),则S1和S2的中位数是11。现在有两个等长的升序序列A和B,试设计在一个时间和空间两方面都尽可能高效的算法,找出两个序列A和B的中位数。
🌰优解
📇优解思路
- 算法思想:
- 检查A和B的中间位置的元素,分别记为a_mid和b_mid。
如果a_mid等于b_mid,那么它们就是两个序列的中位数,直接返回a_mid或b_mid都可以。
如果a_mid小于b_mid,说明A的中位数位于A的后半部分和B的前半部分之间,将A的前半部分和B的后半部分丢弃,继续在剩下的部分中查找中位数。
如果a_mid大于b_mid,说明B的中位数位于B的后半部分和A的前半部分之间,将B的前半部分和A的后半部分丢弃,继续在剩下的部分中查找中位数。
- 重复上述步骤,直到找到中位数。
- 时间复杂度:O(log(min(La, Lb))),其中La和Lb分别是序列A和B的长度。这是因为在每一步中,我们都将输入规模减少一半。
- 空间复杂度:O(1),因为它只使用了一些变量来存储中间结果,而不需要额外的数据结构。
- 备注:这段程序好像不能在网上的在线编译器跑,会显示“‘INT_MIN’ was not declared in this scope”。
⌨️优解代码
#include <iostream>
using namespace std;// 函数:findMedianSortedArrays
// 参数:两个升序数组A和B,以及它们的长度La和Lb
// 返回值:两个数组的中位数
double findMedianSortedArrays(int A[], int B[], int La, int Lb) {// 确保La小于等于Lb,方便后续处理if (La > Lb) {swap(A, B);swap(La, Lb);}// 初始化左边界和右边界,以及两数组的中位数的位置(结果向下取整)int left = 0, right = La;int halfLen = (La + Lb + 1) / 2;// 使用二分查找在数组A中找到合适的位置while (left < right) {int i = left + (right - left) / 2;int j = halfLen - i;int round = 1;// cout << "Round " << round++ << ":" << endl;// cout << "i = " << i << ", j = " << j << endl;// 通过比较A[i]和B[j-1]来调整i的位置if (A[i] < B[j - 1])left = i + 1;elseright = i;// cout << "After comparison, left = " << left << ", right = " << right << endl << endl;}// 计算中位数所在的位置int i = left, j = halfLen - left;// 计算四个关键值,用于求解中位数int AleftMax = (i == 0) ? INT_MIN : A[i - 1]; //如果i等于0(也就是A的左边界),那么将AleftMax设为整型的最小值 INT_MIN(通常是-2147483648)。否则,将AleftMax设为A中下标为i-1的元素的值。int ArightMin = (i == La) ? INT_MAX : A[i];int BleftMax = (j == 0) ? INT_MIN : B[j - 1];int BrightMin = (j == Lb) ? INT_MAX : B[j];// cout << "Final values:" << endl;// cout << "i = " << i << ", j = " << j << endl;// cout << "AleftMax = " << AleftMax << ", ArightMin = " << ArightMin << endl;// cout << "BleftMax = " << BleftMax << ", BrightMin = " << BrightMin << endl;// 根据数组总长度的奇偶性返回中位数if ((La + Lb) % 2 == 1)return max(AleftMax, BleftMax);elsereturn (max(AleftMax, BleftMax) + min(ArightMin, BrightMin)) / 2.0;
}int main() {int A[] = {11, 13, 15, 17, 19}; // 第一个升序数组int B[] = {2, 4, 6, 8, 20}; // 第二个升序数组int La = sizeof(A) / sizeof(A[0]); // 第一个数组的长度,将数组占用内存的总字节数除以第一个元素占用的字节数,我们得到了数组中元素的个数,也就是数组的长度。int Lb = sizeof(B) / sizeof(B[0]); // 第二个数组的长度double median = findMedianSortedArrays(A, B, La, Lb); // 调用函数计算中位数cout << "中位数是: " << median << endl; // 输出中位数return 0;
}
⌨️优解演算
初始:
int A[] = {11, 13, 15, 17, 19};
int B[] = {2, 4, 6, 8, 20};
int La = 5;
int Lb = 5;
halfLen = (La + Lb + 1) / 2 = (5 + 5 + 1) / 2 = 11 / 2 = 5;
left = 0;
right = La = 5;第一轮循环:
i = 0 + ( 5 - 0 ) / 2 = 2, j = 5 - 2 = 3;
A[i = 2] = 15, B[j - 1 = 2] = 6;
A[i] 大于 B[j - 1],所以更新 right = i = 2第二轮循环:
i = 0 + ( 2 - 0 ) / 2 = 1, j = 5 - 1 = 4;
A[i = 1] = 13, B[4 - 1 = 3] = 8;
A[i] 大于 B[j - 1],所以更新 right = i = 1第三轮循环:
i = 0 + ( 1 - 0 ) / 2 = 0, j = 5 - 0 = 5;
A[i = 0] = 11, B[5 - 1 = 4] = 20;
A[i] 小于 B[j - 1],所以更新 left = j = 1不满足while循环条件,跳出:
i = j = 1; j = 5-1 = 4;
AleftMax = A[i-1] = 11, ArightMin = A[1] = 13;
BleftMax = B[j-1] = 8, BrightMin = B[j] = 20;(La + Lb) % 2 = (5 + 5) % 2 = 10 % 2 = 0;
max(AleftMax, BleftMax) + min(ArightMin, BrightMin)) / 2.0 = max(11+13)/2 =12
🌰暴力解
📇暴力解思路
- 算法思想:将两个数组合并后排序,然后找到合并后数组的中位数;
- 时间复杂度:O(La + Lb);
- 空间复杂度:O(La + Lb);
⌨️暴力解代码
#include <iostream>
#include <vector>
using namespace std;double findMedianSortedArrays(int A[], int B[], int La, int Lb) {// 将数组A和数组B合并到一个新的数组C中vector<int> C;int i = 0, j = 0;while (i < La && j < Lb) {if (A[i] <= B[j]) {C.push_back(A[i]);i++;} else {C.push_back(B[j]);j++;}}while (i < La) {C.push_back(A[i]);i++;}while (j < Lb) {C.push_back(B[j]);j++;}// 计算合并后数组C的长度int Lc = C.size();// 计算中位数的位置int mid = Lc / 2;if (Lc % 2 == 1) {return C[mid];} else {return (C[mid - 1] + C[mid]) / 2.0;}
}int main() {int A[] = {11, 13, 15, 17, 19};int B[] = {2, 4, 6, 8, 20};int La = sizeof(A) / sizeof(A[0]);int Lb = sizeof(B) / sizeof(B[0]);double median = findMedianSortedArrays(A, B, La, Lb);cout << "中位数是: " << median << endl;return 0;
}⌨️暴力解演算
- int A[] = {11, 13, 15, 17, 19}; int B[] = {2, 4, 6, 8, 20};
- vector<int> C = {2, 4, 6, 8, 11, 13, 15, 17, 19};
Lc = (C[4 ]+ C[5])/2 = 12;
🧵2013统考真题
🧩题目
已知一个整数序列A=(a0,a1,…,an),其中0≤ai≤n。若存在ap1=ap2=…=apm=x 且 m > n/2 (0≤pk<n,1≤k≤m),则称x为A的主元素。例如A=(0,5,5,3,5,7,5,5),则5为主元素;又如A=(0,5,5,3,5,1,5,7),则A中没有主元素。假设A中的n个元素保存在一个一维数组中,请设计一个尽可能高效的算法,找出A的主元素。若存在主元素,则输出该元素;否则输出-1。
🌰优解
📇优解思路
- 算法思想:"摩尔投票算法"
- 遍历数组并维护一个候选主元素以及一个计数器;
- 在遍历过程中,如果计数器为零,就将当前元素设为候选主元素;否则,如果当前元素与候选主元素相同,计数器增加,否则计数器减少。最后剩下的候选主元素可能就是主元素;
- 但还需要再次遍历数组确认它是否真的满足主元素的条件。
- 时间复杂度:O(n),其中n是输入数组的长度。算法需要进行两次遍历,每次遍历的时间复杂度都是O(n)。
- 空间复杂度:O(1),因为它只使用了常数级别的额外空间来存储候选主元素和计数器,而不随输入规模变化。
⌨️优解代码
#include <iostream>
using namespace std;int findMajorityElement(int A[], int n) {int candidate = -1;int count = 0;// 第一轮遍历,选出候选主元素for (int i = 0; i < n; i++) {// cout << "candidate = A[" << i << "] = " << candidate << ", count = " << count << endl;if (count == 0) {candidate = A[i];count = 1;} else {if (A[i] == candidate) {count++;} else {count--;}}}// 第二轮遍历,确认候选主元素是否真的是主元素count = 0;for (int i = 0; i < n; i++) {if (A[i] == candidate) {count++;}}// cout << "count = " << count << endl;if (count > n / 2) {return candidate;} else {return -1;}
}int main() {int A[] = {0, 5, 5, 3, 5, 7, 5, 5};int B[] = {0, 5, 5, 3, 5, 1, 5, 7};int La = sizeof(A) / sizeof(A[0]);int Lb = sizeof(B) / sizeof(B[0]);int resultA = findMajorityElement(A, La);int resultB = findMajorityElement(B, Lb);if (resultA != -1) {cout << "数组A的主元素是:" << resultA << endl;} else {cout << "数组A没有主元素" << endl;}if (resultB != -1) {cout << "数组B的主元素是:" << resultB << endl;} else {cout << "数组B没有主元素" << endl;}return 0;
}
⌨️优解演算
数组A
candidate = A[0] = -1, count = 0
candidate = A[1] = 0, count = 1
candidate = A[2] = 0, count = 0
candidate = A[3] = 5, count = 1
candidate = A[4] = 5, count = 0
candidate = A[5] = 5, count = 1
candidate = A[6] = 5, count = 0
candidate = A[7] = 5, count = 1
count = 5,count > 8/2数组B
candidate = A[0] = -1, count = 0
candidate = A[1] = 0, count = 1
candidate = A[2] = 0, count = 0
candidate = A[3] = 5, count = 1
candidate = A[4] = 5, count = 0
candidate = A[5] = 5, count = 1
candidate = A[6] = 5, count = 0
candidate = A[7] = 5, count = 1
count = 4,count ≤ 8/2
🌰暴力解
📇暴力解思路
- 算法思想:
- 统计每种元素的出现次数,然后找到出现次数最多的元素。
- 第一遍遍历数组,统计每种元素的出现次数,可以使用一个哈希表或者数组来存储。
- 第二遍遍历统计结果,找到出现次数最多的元素。
- 检查该元素的出现次数是否大于总长度除以2,如果满足条件,则它是主元素,否则不存在主元素。
- 时间复杂度:O(n),其中n是输入数组的长度。
- 空间复杂度:O(n),取决于不同元素的数量,最坏情况下可能会达到O(n)。
⌨️暴力解代码
#include <iostream>
#include <unordered_map>
using namespace std;int findMajorityElement(int A[], int n) {// 使用哈希表 counter 统计每个元素的出现次数unordered_map<int, int> counter;// 第一次遍历,统计每个元素的出现次数for (int i = 0; i < n; i++) {counter[A[i]]++;}// 测试:输出哈希表的值// cout << "Counter:" << endl;// for (auto& pair : counter) {// cout << pair.first << ": " << pair.second << endl;// }// 找到出现次数最多的元素int maxCount = 0;int majorityElement = -1;for (auto& pair : counter) { // 声明一个名为 pair 的变量,它的类型会根据 counter 中的元素类型自动推断(因为我们使用了 auto)。pair 实际上是一个键值对,包括一个键(pair.first)和一个值(pair.second)。// 测试:输出所有参数的值// cout << "pair.first = " << pair.first << ", pair.second = " << pair.second << endl;// cout << "maxCount = " << maxCount << ", majorityElement = " << majorityElement << endl;if (pair.second > maxCount) { // 比较当前键值对的值(也就是元素出现的次数 pair.second)和 maxCount 的大小maxCount = pair.second; // 如果当前元素出现的次数大于 maxCount,则更新 maxCount 和 majorityElementmajorityElement = pair.first; // 将当前元素作为候选主元素}}// 检查出现次数是否大于总长度的一半if (maxCount > n / 2) {return majorityElement;} else {return -1;}
}int main() {int A[] = {0, 5, 5, 3, 5, 7, 5, 5};int B[] = {0, 5, 5, 3, 5, 1, 5, 7};int La = sizeof(A) / sizeof(A[0]);int Lb = sizeof(B) / sizeof(B[0]);int resultA = findMajorityElement(A, La);int resultB = findMajorityElement(B, Lb);if (resultA != -1) {cout << "数组A的主元素是:" << resultA << endl;} else {cout << "数组A没有主元素" << endl;}if (resultB != -1) {cout << "数组B的主元素是:" << resultB << endl;} else {cout << "数组B没有主元素" << endl;}return 0;
}⌨️暴力解演算
- 数组A模拟:
Counter:
3: 1
7: 1
0: 1
5: 5
pair.first = 3, pair.second = 1
maxCount = 0, majorityElement = -1
pair.first = 7, pair.second = 1
maxCount = 1, majorityElement = 3
pair.first = 0, pair.second = 1
maxCount = 1, majorityElement = 3
pair.first = 5, pair.second = 5
maxCount = 1, majorityElement = 3
数组A的主元素是:5
- 数组B模拟:
Counter:
1: 1
3: 1
7: 1
0: 1
5: 4
pair.first = 1, pair.second = 1
maxCount = 0, majorityElement = -1
pair.first = 3, pair.second = 1
maxCount = 1, majorityElement = 1
pair.first = 7, pair.second = 1
maxCount = 1, majorityElement = 1
pair.first = 0, pair.second = 1
maxCount = 1, majorityElement = 1
pair.first = 5, pair.second = 4
maxCount = 1, majorityElement = 1
数组B没有主元素
🧵2018统考真题
🧩题目
给定一个含n个整数的数组,请设计一个在时间上尽可能高效的算法,找出数组中未出现的最小正整数。例如,数组{-5,3,2,3}中未出现的最小正整数是1,数组{1,2,3}中未出现的最小正整数是4。
🌰优解
📇优解思路
- 算法思想:"哈希表标记"
- 利用数组本身来进行标记,将数组元素放置到其对应的位置上;
- 然后再遍历一次数组找出第一个不符合规则的位置,即未出现的最小正整数。
- 时间复杂度:O(n),因为最多需要遍历两次数组。
- 空间复杂度:O(n),使用了一个大小与输入数组相同的数组进行操作,因此空间复杂度是线性的,与输入数组的大小成正比。
- 备注:这个算法思想应该还是挺容易想到的,因此没有暴力解。
⌨️优解代码
#include <iostream>
#include <vector>
using namespace std;int firstMissingPositive(vector<int>& nums) {int n = nums.size();// 将数组元素放置到其对应的位置上for (int i = 0; i < n; ++i) {while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {swap(nums[i], nums[nums[i] - 1]);}}// 再次遍历数组,找出第一个不符合规则的位置for (int i = 0; i < n; ++i) {if (nums[i] != i + 1) {return i + 1;}}return n + 1; // 如果数组本身符合规则,则返回数组长度加1
}int main() {vector<int> arr1 = {-5, 3, 2, 3};vector<int> arr2 = {1, 2, 3};int missing1 = firstMissingPositive(arr1);int missing2 = firstMissingPositive(arr2);cout << "数组{-5, 3, 2, 3}中未出现的最小正整数是:" << missing1 << endl;cout << "数组{1, 2, 3}中未出现的最小正整数是:" << missing2 << endl;return 0;
}
🧵2020统考真题
🧩题目
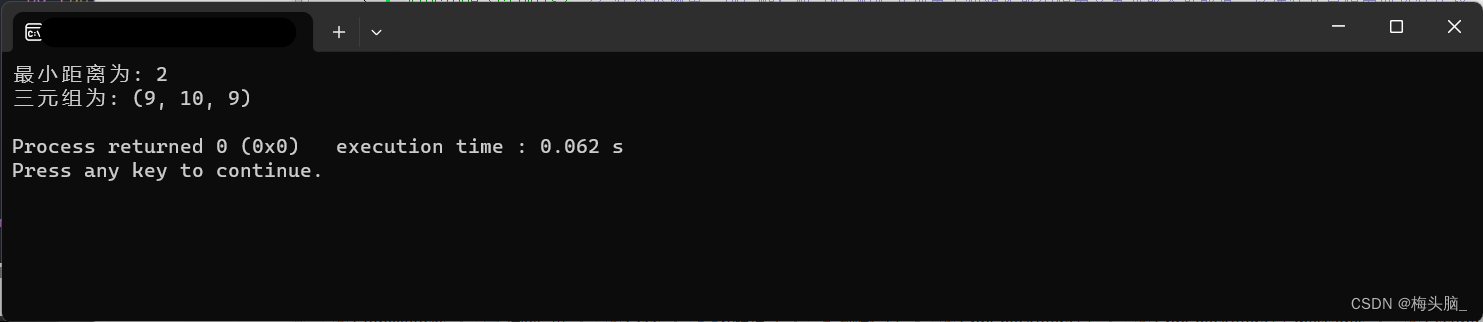
定义三元组(a,b,c)(a,b,c均为整数)的距离D=|a-b| + |b-c| + |c-a|。给定3个非空整数集合S1、S2和S3,按升序分别存储在3个数组中。请设计一个尽可能高效的算法,计算并输出所有可能得三元组(a,b,c)(a∈S1,b∈S2,c∈S3)中的最小距离、例如S1={-1,0,9},S2={-25,-10,-10,11},S3={2,9,17,30,41},则最小距离为2,相应的三元组为(9,10,9)。
🌰优解
📇优解思路
- 通用思路:在求解距离的问题中,通常的做法是通过遍历或者适当的比较来不断更新最小值。这种方法通常会在处理多个元素之间的关系时有效,尤其是在找到最小值或最大值时。
- 算法思想:
- 选择S1、S2和S3中的一个数作为其中一个元素(比如选择S1中的元素作为a);
- 然后在S2和S3中使用两个指针分别找到与a最接近的b和c,从而计算距离,并维护最小距离;
- 时间复杂度:O(n),emm...如果忽略那段蠢萌的vector输出的话;
- 空间复杂度:O(1),除了用于存储输入数组外,算法中没有使用额外的辅助空间。
⌨️优解代码
#include <iostream>
#include <vector>
#include <climits> // 在本示例中,INT_MAX 和 INT_MIN 分别用于初始化最小距离变量为最大可能值,以便在计算距离时进行比较,并找到最小值。
using namespace std;int minDistanceTriplet(vector<int>& S1, vector<int>& S2, vector<int>& S3) {int minDistance = INT_MAX;int i = 0, j = 0, k = 0;int size1 = S1.size(), size2 = S2.size(), size3 = S3.size();while (i < size1 && j < size2 && k < size3) {int a = S1[i], b = S2[j], c = S3[k];int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);minDistance = min(minDistance, currentDistance);// 找到与当前 a 最接近的 bif (a <= b && a <= c) {i++;} else if (b <= a && b <= c) {j++;} else {k++;}}return minDistance;
}void printTriplet(int a, int b, int c) {cout << "三元组为: (" << a << ", " << b << ", " << c << ")" << endl;
}int main() {vector<int> S1 = {-1, 0, 9};vector<int> S2 = {-25, -10, 10, 11};vector<int> S3 = {2, 9, 17, 30, 41};int minDist = minDistanceTriplet(S1, S2, S3);cout << "最小距离为: " << minDist << endl;// 输出三元组// 遍历三元组的索引,根据索引取得对应元素输出for (int i = 0; i < S1.size(); ++i) {for (int j = 0; j < S2.size(); ++j) {for (int k = 0; k < S3.size(); ++k) {int a = S1[i], b = S2[j], c = S3[k];int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);if (currentDistance == minDist) {printTriplet(a, b, c);}}}}return 0;
}
🌰暴力解
📇暴力解思路
- 算法思想:
- 使用三重循环来遍历所有可能的三元组;
- 计算每个三元组的距离并更新最小值;
- 时间复杂度:O(n),其中n是输入数组的长度;
- 空间复杂度:O(1)。
⌨️暴力解代码
#include <iostream>
#include <vector>
#include <climits> // 在本示例中,INT_MAX 和 INT_MIN 分别用于初始化最小距离变量为最大可能值,以便在计算距离时进行比较,并找到最小值。
using namespace std;int minDistanceTriplet(vector<int>& S1, vector<int>& S2, vector<int>& S3) {int minDistance = INT_MAX;for (int i = 0; i < S1.size(); ++i) {for (int j = 0; j < S2.size(); ++j) {for (int k = 0; k < S3.size(); ++k) {int a = S1[i], b = S2[j], c = S3[k];int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);minDistance = min(minDistance, currentDistance);}}}return minDistance;
}void printTriplet(int a, int b, int c) {cout << "三元组为: (" << a << ", " << b << ", " << c << ")" << endl;
}int main() {vector<int> S1 = {-1, 0, 9};vector<int> S2 = {-25, -10, 10, 11};vector<int> S3 = {2, 9, 17, 30, 41};int minDist = minDistanceTriplet(S1, S2, S3);cout << "最小距离为: " << minDist << endl;// 输出三元组// 遍历三元组的索引,根据索引取得对应元素输出for (int i = 0; i < S1.size(); ++i) {for (int j = 0; j < S2.size(); ++j) {for (int k = 0; k < S3.size(); ++k) {int a = S1[i], b = S2[j], c = S3[k];int currentDistance = abs(a - b) + abs(b - c) + abs(c - a);if (currentDistance == minDist) {printTriplet(a, b, c);}}}}return 0;
}🔚结语
博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容{例如有错误、难理解、不简洁、缺功能}等,博主会顶锅前来修改~😶🌫️
我是梅头脑,本片博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下,收到点赞的话,博主肝文的动力++~🌟🌟
数据结构_梅头脑_的博客-CSDN博客![]() https://blog.csdn.net/weixin_42789937/category_12262100.html?spm=1001.2014.3001.5482
https://blog.csdn.net/weixin_42789937/category_12262100.html?spm=1001.2014.3001.5482
相关文章:
数据结构02附录01:顺序表考研习题[C++]
图源:文心一言 考研笔记整理~🥝🥝 之前的博文链接在此:数据结构02:线性表[顺序表链表]_线性链表-CSDN博客~🥝🥝 本篇作为线性表的代码补充,每道题提供了优解和暴力解算法…...
ClientDateSet:Cannot perform this operation on a closed dataset
一、问题表现 Delphi 三层DataSnap,使用AlphaControls控件优化界面,一窗口编辑时,出现下列错误提示: 编译通过,该窗口中,重新显示数据,下图: 相关代码: procedure…...

python中列表的基础解释
列表: 一种可以存放多种类型数据的数据结构 列表的创建: 1.用【】创建列表 #创建一个空列表 list1[] #创建一个非空列表 list2 [zhang,li,ying,1,2,3] #输出内容及类型 print(list1,type(list1)) print(list2,type(list2))结果: 2.使用list…...

『力扣刷题本』:链表分割
一、题目 现有一链表的头指针 ListNode* pHead,给一定值x,编写一段代码将所有小于x的结点排在其余结点之前,且不能改变原来的数据顺序,返回重新排列后的链表的头指针。 二、思路解析 首先,让我们列出我们需要做的事情&…...
FISCOBCOS入门(十)Truffle测试helloworld智能合约
本文带你从零开始搭建truffle以及编写迁移脚本和测试文件,并对测试文件的代码进行解释,让你更深入的理解truffle测试智能合约的原理,制作不易,望一键三连 在windos终端内安装truffle npm install -g truffle 安装truffle时可能出现网络报错,多试几次即可 truffle --vers…...

Unity Text文本首行缩进两个字符的方法
Text文本首行缩进两个字符的方法比较简单。通过代码把"\u3000\u3000"加到文本字符串前面即可。 参考如下代码: TMPtext1.text "\u3000\u3000" "这是一段有首行缩进的文本内容。\n这是第二行"; 运行效果如下图所示: 虽…...

TS的函数重载、类型合并、类型断言
函数重载 let list5 [1, 2, 3, 4]function findNum(id: number): number[]function findNum(): number[]function findNum(list: number[]): number[]function findNum(ids?: number | number[]): number[] {if (typeof ids number) {return list5.filter((num) > num …...

JVM:字节码文件,类的生命周期,类加载器
JVM:字节码文件,类的生命周期,类加载器 为什么要学这门课程 1. 初识JVM1.1. 什么是JVM1.2. JVM的功能1.3. 常见的JVM 2. 字节码文件详解2.1. Java虚拟机的组成2.2. 字节码文件的组成2.2.1. 以正确的姿势打开文…...
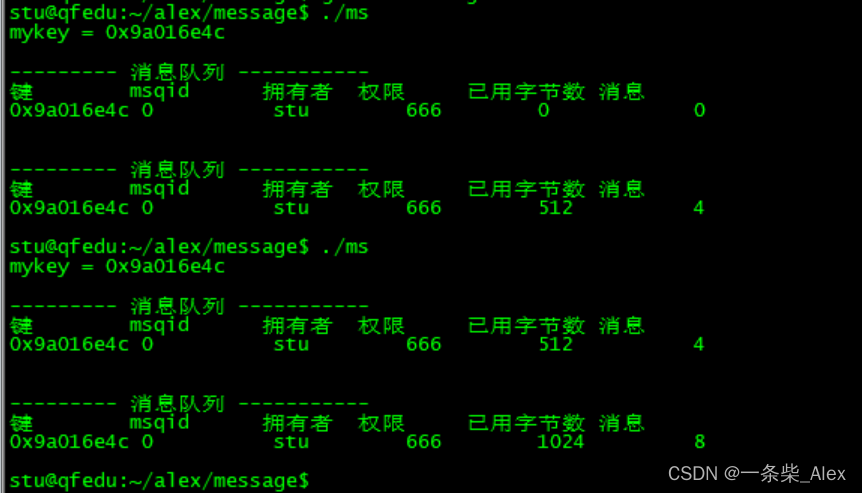
【IPC】消息队列
1、IPC对象 除了最原始的进程间通信方式信号、无名管道和有名管道外,还有三种进程间通信方式,这 三种方式称之为IPC对象 IPC对象分类:消息队列、共享内存、信号量(信号灯集) IPC对象也是在内核空间开辟区域,每一种IPC对象创建好…...
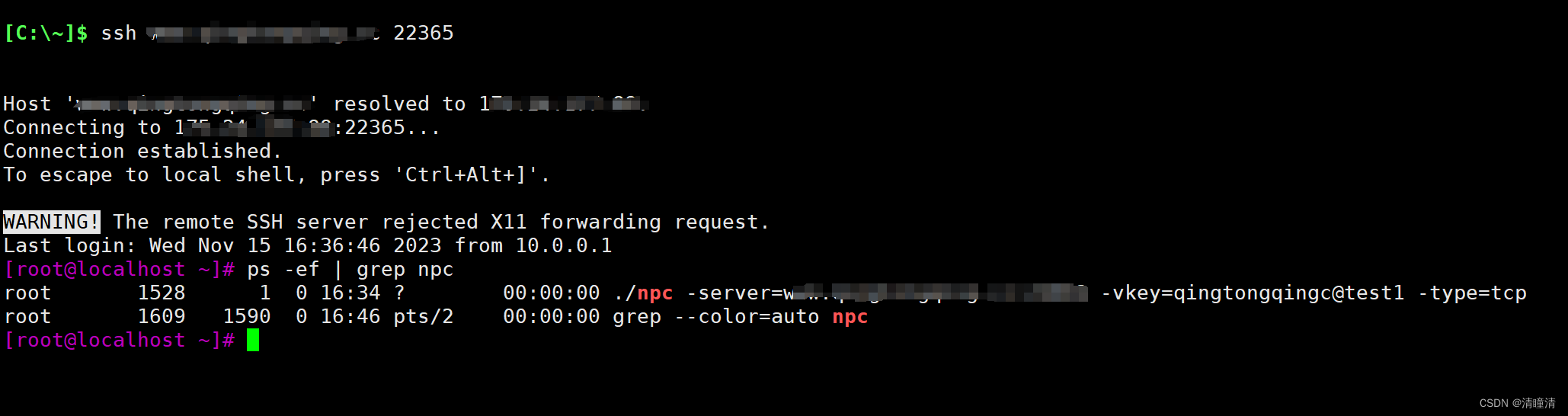
内网穿透工具NPS(保姆级教程)
前言: 有时候我们受限于硬件设备和网络的的问题,无法将内网的大容量、高性能存储设备或计算设备对外访问。这个时候就会变的特别苦恼,上云呢成本太大,不用云呢公网又无法直接访问,这个时候怎么办呢,NPS它来…...

最长公共子序列问题
构造最长公共子序列为什么要这样构造序列 for(int i1;i<n;i){int k;cin>>k;b[k]i;}for(int i1;i<n;i){int k;cin>>k;a[i]b[k];}并且为什么要求上升序列,是有什么数学知识包含在其中吗? 为什么在求最长公共子序列时,f[mid]大…...

服务器数据恢复—热备盘同步中断导致Raid5数据丢失的数据恢复案例
服务器数据恢复环境: 某单位一台服务器上有一组raid5阵列,该raid5阵列有15块成员盘。上层是一个xfs裸分区,起始位置是0扇区。 服务器故障&检测: 服务器raid5阵列中有硬盘性能表现不稳定,但是由于管理员长时间没有关…...

桥接模式-C++实现
桥接模式是一种结构型设计模式,它是将抽象部分和实现部分隔离,通过组合关系将抽象部分和实现部分解耦,使它们可以独立变化。 因此,桥接模式可以很好的处理两个或两个以上维度的变化。 举一个例子说明: 假设我们现在…...

PHP字符串函数的解析
在PHP中,字符串是一种常见的数据类型,用于存储和操作文本数据。PHP提供了丰富的字符串函数,用于执行各种字符串操作,包括截取、连接、替换、搜索等。在这篇文章中,我们将深入解析一些常用的PHP字符串函数,以…...

科研学习|研究方法——使用python强大的Statsmodel 执行假设检验和线性回归
如果你使用 Python 处理数据,你可能听说过 statsmodel 库。 Statsmodels 是一个 Python 模块,它提供各种统计模型和函数来探索、分析和可视化数据。该库广泛用于学术研究、金融和数据科学。 在本文中,我们将介绍 statsmodel 库的基础知识、如…...

设计模式——责任链模式
文章目录 责任链模式的定义场景示例责任链模式实现方案责任链模式扩展责任链模式的优缺点责任链模式在框架源码中的应用 责任链模式的定义 责任链模式又称职责链模式,是一种行为型设计模式。官方描述:使多个对象都有机会处理请求,从而避免请…...

nginx得if语句内proxy_pass不允许携带url部分,如何处理
在nginx中,proxy_pass指令不能直接携带URL部分。但是,可以使用rewrite指令结合正则表达式来处理URL部分。 下面是一个示例配置,演示如何使用rewrite指令将URL中的某个部分进行替换后传递给后端服务器: location /v100/{proxy_…...

CentOS7设置 redis 开机自启动
CentOS7设置 redis 开机自启动 步骤1.创建redis.service文件2.重新加载所有服务3.设置开机自启动4.自由地使用linux系统命令4.1.启动 Redis 服务4.2.查看 Redis 状态(-l:查看完整的信息)4.3.停止 Redis 服务4.4.重启 Redis 服务 步骤 如果你傲娇,不想拷贝࿰…...
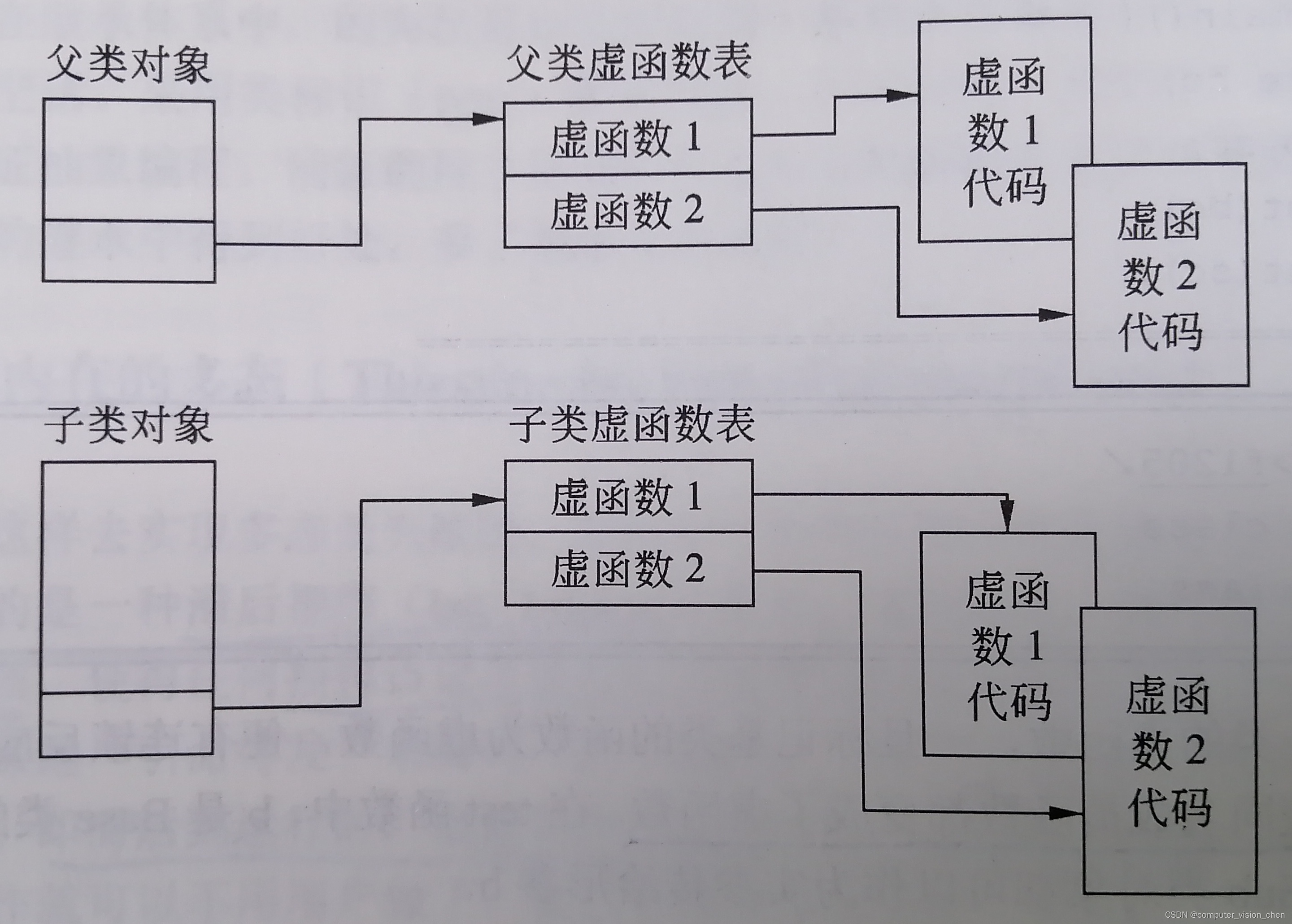
C++虚函数(定义,作用,原理,案例)
一.定义: C的虚函数是在父类(基类)中声明的的函数,它可在子类(派生类)中重写。二.作用 虚函数的目的是实现多态性,即在程序运行时根据对象的实际类型确定调用哪个函数。三.使用方法: 在基类中声明虚函数时,需要在函…...

C#中.NET 6.0 控制台应用通过EF访问新建数据库
目录 一、 操作步骤 二、编写EF模型和数据库上下文 三、 移植(Migrations)数据库 四、编写应用程序并运行 前文已经说过.NET Framework4.8 控制台应用通过EF访问新建数据库,这里的数据据库要根据事先编写好的EF模型、经过一番操作&#x…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...
: 发布订阅模式)
JS设计模式(5): 发布订阅模式
解锁JavaScript发布订阅模式:让代码沟通更优雅 在JavaScript的世界里,我们常常会遇到这样的场景:多个模块之间需要相互通信,但是又不想让它们产生过于紧密的耦合。这时候,发布订阅模式就像一位优雅的信使,…...
