基于世界杯算法优化概率神经网络PNN的分类预测 - 附代码
基于世界杯算法优化概率神经网络PNN的分类预测 - 附代码
文章目录
- 基于世界杯算法优化概率神经网络PNN的分类预测 - 附代码
- 1.PNN网络概述
- 2.变压器故障诊街系统相关背景
- 2.1 模型建立
- 3.基于世界杯优化的PNN网络
- 5.测试结果
- 6.参考文献
- 7.Matlab代码
摘要:针对PNN神经网络的光滑因子选择问题,利用世界杯算法优化PNN神经网络的光滑因子的选择,并应用于变压器故障诊断。
1.PNN网络概述
概率神经网络( probabilistic neural networks , PNN )是 D. F. Specht 博士在 1 989 年首先提出的,是一种基于 Bayes 分类规则与 Parzen窗的概率密度面数估计方法发展而来的并行算 法。它是一类结胸简单、训练简洁、应用广泛的人工神经网络 。在实际应用中,尤其是在解决分类问题的应用中, PNN 的优势在于用线性学习算法来完成非线性学 习算法所傲的工作,同 时保持非线性算法的高精度等特性;这种网络对应的权值就是模式样本的分布,网络不需要训练,因而能够满足训练上实时处理的要求。
PNN 网络是由径向基函数网络发展而来的一种前馈型神经网络,其理论依据是贝叶斯最小风险准则(即贝叶斯决策理论), PNN作为径向基网络的一种,适合于模式分类。当分布密度 SPREAD 的值接近于 0 时,它构成最邻分类器; 当 SPREAD 的值较大时,它构成对几个训练样本的临近分类器 。 PNN 的层次模型,由输入层、模式层、求和层、输出层共 4 层组成 , 其基本结构如图 1 所示。
f ( X , w i ) = e x p [ − ( X − w i ) T ( X − W i ) / 2 δ ] (1) f(X,w_i)=exp[-(X-w_i)^T(X-W_i)/2\delta]\tag{1} f(X,wi)=exp[−(X−wi)T(X−Wi)/2δ](1)
式中, w i w_i wi为输入层到模式层连接的权值 ; δ \delta δ为平滑因子,它对分类起着至关重要的作用。第 3 层是求和层,是将属于某类的概率累计 ,按式(1)计算 ,从而得到故障模式的估计概率密度函数。每一类只有一个求和层单元,求和层单元与只属于自己类的模式层单元相连接,而与模式层中的其他单元没有连接。因此求和层单元简单地将属于自己类的模式层单元 的输出相加,而与属于其他类别的模式层单元的输出无关。求和层单元的输出与各类基于内 核的概率密度的估计成比例,通过输出层的归一化处理 , 就能得到各类的概率估计。网络的输 出决策层由简单的阔值辨别器组成,其作用是在各个故障模式的估计概率密度中选择一个具 有最大后验概率密度的神经元作为整个系统的输出。输出层神经元是一种竞争神经元,每个神经元分别对应于一个数据类型即故障模式,输出层神经元个数等于训练样本数据的种类个 数,它接收从求和层输出的各类概率密度函数,概率密度函数最大的那个神经元输出为 1 ,即 所对应的那一类为待识别的样本模式类别,其他神经元的输出全为 0 。

2.变压器故障诊街系统相关背景
运行中的变压器发生不同程度的故障时,会产生异常现象或信息。故障分析就是搜集变压器的异常现象或信息,根据这些现象或信息进行分析 ,从而判断故障的类型 、严重程度和故障部位 。 因此 , 变压器故障诊断的目的首先是准确判断运行设备当前处于正常状态还是异常状态。若变压器处于异常状态有故障,则判断故障的性质、类型和原因 。 如是绝缘故障、过热故障还是机械故障。若是绝缘故障,则是绝缘老化 、 受潮,还是放电性故障 ;若是放电性故障又 是哪种类型的放电等。变压器故障诊断还要根据故障信息或根据信息处理结果,预测故障的可能发展即对故障的严重程度、发展趋势做出诊断;提出控制故障的措施,防止和消除故障;提出设备维修的合理方法和相应的反事故措施;对设备的设计、制造、装配等提出改进意见,为设备现代化管理提供科学依据和建议。
2.1 模型建立
本案例在对油中溶解气体分 析法进行深入分析后,以改良三比值法为基础,建立基于概率神经网络的故障诊断模型。案例数据中的 data. mat 是 33 × 4 维的矩阵,前3列为改良三比值法数值,第 4 列为分类的输出,也就是故障的类别 。 使用前 23 个样本作为 PNN 训练样本,后10个样本作为验证样本 。
3.基于世界杯优化的PNN网络
世界杯算法原理请参考:https://blog.csdn.net/u011835903/article/details/120418580
利用世界杯算法对PNN网络的光滑因子进行优化。适应度函数设计为训练集与测试集的分类错误率:
f i t n e s s = a r g m i n { T r a i n E r r o r R a t e + P r e d i c t E r r o r R a t e } (2) fitness = argmin\{TrainErrorRate + PredictErrorRate\}\tag{2} fitness=argmin{TrainErrorRate+PredictErrorRate}(2)
适应度函数表明,如果网络的分类错误率越低越好。
5.测试结果
世界杯参数设置如下:
%% 世界杯参数
pop=20; %种群数量
Max_iteration=20; % 设定最大迭代次数
dim = 1;%维度,即权值与阈值的个数
lb = 0.01;%下边界
ub = 5;%上边界



从结果来看,世界杯-pnn能够获得好的分类结果。
6.参考文献
书籍《MATLAB神经网络43个案例分析》,PNN原理部分均来自该书籍
7.Matlab代码
相关文章:

基于世界杯算法优化概率神经网络PNN的分类预测 - 附代码
基于世界杯算法优化概率神经网络PNN的分类预测 - 附代码 文章目录 基于世界杯算法优化概率神经网络PNN的分类预测 - 附代码1.PNN网络概述2.变压器故障诊街系统相关背景2.1 模型建立 3.基于世界杯优化的PNN网络5.测试结果6.参考文献7.Matlab代码 摘要:针对PNN神经网络…...
NPM 与 XUI 共存!Nginx Proxy Manager 搭配 X-UI 实现 Vless+WS+TLS 教程!
之前分享过搭建可以与宝塔共存的一个 “魔法” 服务器状态监控应用 ——xui,支持 VmessWSTLS。 最近 Docker 视频出的比较多,前阵子又出现了宝塔国内版存在隐私泄露的问题,很多小伙伴其实都不用宝塔了,那么,在我们现在…...

【网络奇遇记】那年我与计算机网络的浅相知
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 一. 计算机网络的定义1.1 计算机早期的一个最简单的定义1.2 现阶段计算机网络的一个较好的定义 二. …...
)
LeetCode26.删除有序数组中的重复项(双指针法)
LeetCode26.删除有序数组中的重复项 1.问题描述2.解题思路3.代码 1.问题描述 给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然…...

原型网络Prototypical Network的python代码逐行解释,新手小白也可学会!!-----系列8
文章目录 前言一、原始代码二、对每一行代码的解释:总结 前言 这是该系列原型网络的最后一段代码及其详细解释,感谢各位的阅读! 一、原始代码 if __name__ __main__:##载入数据labels_trainData, labels_testData load_data() # labels_…...

黑马点评回顾 redis实现共享session
文章目录 传统session缺点整体访问流程代码实现生成验证码登录 问题具体思路 传统session缺点 传统单体项目一般是把session存入tomcat,但是每个tomcat中都有一份属于自己的session,假设用户第一次访问第一台tomcat,并且把自己的信息存放到第一台服务器…...

Redis篇---第八篇
系列文章目录 文章目录 系列文章目录前言一、说说 Redis 哈希槽的概念?二、Redis 常见性能问题和解决方案有哪些?三、假如 Redis 里面有 1 亿个 key,其中有 10w 个 key 是以某个固定的已知的前缀开头的,如果将它们全部找出来?前言 前些天发现了一个巨牛的人工智能学习网站…...

Unity使用Visual Studio Code 调试
Unity 使用Visual Studio Code 调试C# PackageManager安装Visual Studio EditorVisual Studio Code安装Unity 插件修改Unity配置调试 PackageManager安装Visual Studio Editor 打开 Window->PackageManger卸载 Visual Studio Code Editor ,这个已经被官方废弃安…...

【Linux】进程替换|exec系列函数
文章目录 一、看一看单进程版的进程替换二、进程替换的原理三、多进程版——验证各种程序替换接口exec系列函数execlexeclpexecvexecvp tipsexecleexecve 四、总结 一、看一看单进程版的进程替换 #include<stdio.h> #include<unistd.h> #include<stdlib.h>i…...

Java编程技巧:将图片导出成pdf文件
目录 一、pom依赖二、代码三、测试链接 一、pom依赖 <!-- pdf插件 start --> <dependency><groupId>com.itextpdf</groupId><artifactId>itextpdf</artifactId><version>5.5.3</version> </dependency> <dependency…...

二项分布和泊松分布
一、二项分布 1.1 n重伯努利试验 若是二项分布,则必是n重伯努利试验概型。即:每次试验只有两种结果 与 ,且在每次试验中A发生的概率相等,即P(A)p,将这种试验独立重复n次,则称这种试验为n重伯努利试验&#…...

【飞控调试】DJIF450机架+Pixhawk6c mini+v1.13.3固件+好盈Platinium 40A电调无人机调试
1 背景 由于使用了一种新的航电设备组合,在调试无人机起飞的时候遇到了之前没有遇到的问题。之前用的飞控(Pixhawk 6c)和电调(Hobbywing X-Rotor 40A),在QGC里按默认参数配置来基本就能平稳飞行࿰…...
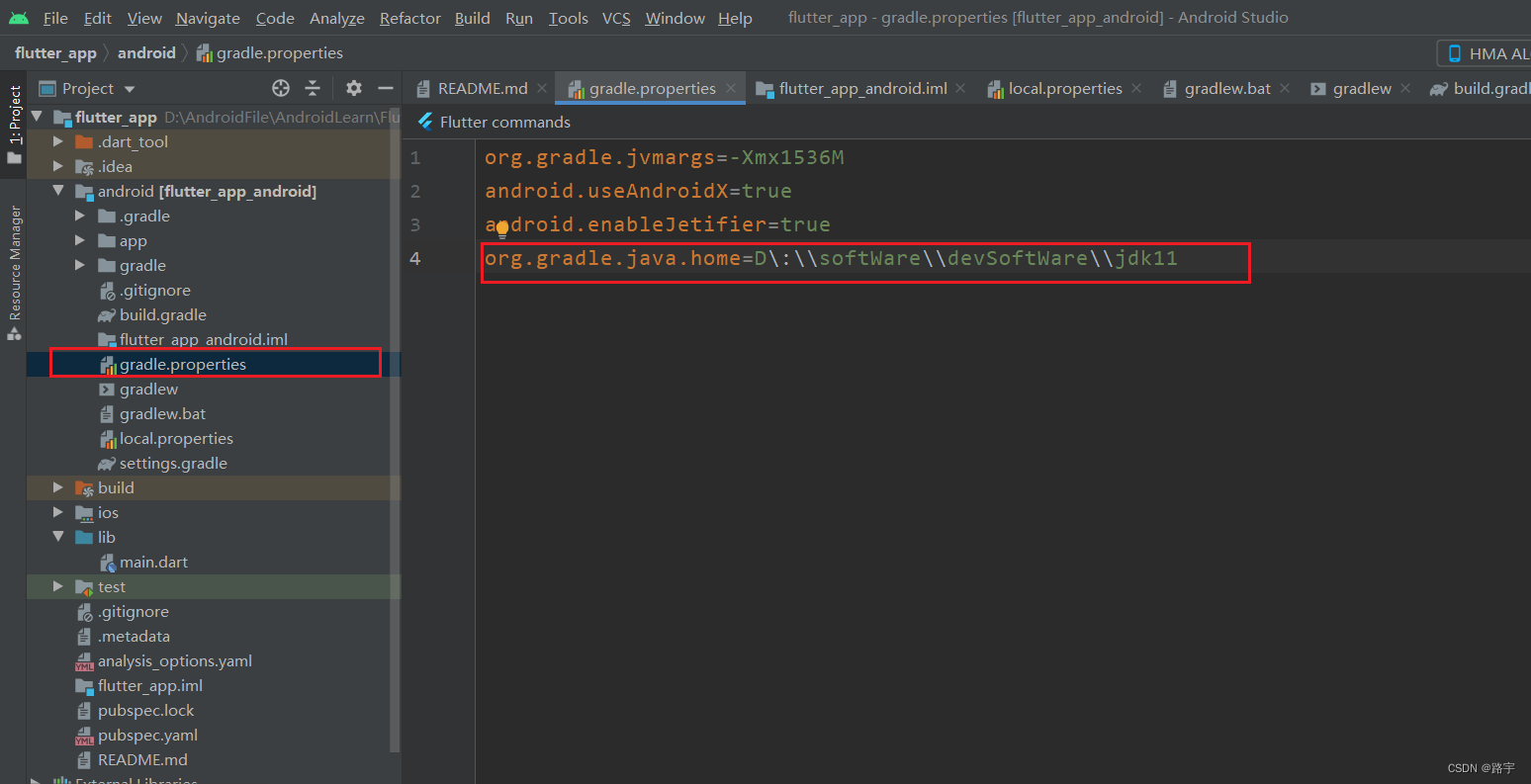
Android studio配置Flutter开发环境报错问题解决
博主前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住也分享一下给大家 👉点击跳转到教程 报错问题截图 报错原因已经给出: You need Java 11 or higher to build your app with this version of G…...

2023.11.18 -自用hadoop高可用环境搭建命令
启动hadoop高可用环境 # 1.先恢复快照到高可用环境 # 2.三台服务器启动zookeeper服务 [rootnode1 ~]# zkServer.sh start [rootnode2 ~]# zkServer.sh start [rootnode3 ~]# zkServer.sh start 查看服务状态: [rootnode]# zkServer.sh status 关闭zk服务的命令是: [rootnode]# …...

【Linux】常用系统工作命令
一、Linux文档目录结构 在Linux系统中,目录、字符设备、套接字、硬盘、光驱、打印机等都被抽象成文件形式,“Linux系统中一切都是文件”。Linux系统中的一切文件都是从"根"目录(/)开始的,并按照文件系统层次…...

深入理解网络协议:通信世界的基石
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 在当今数字化时代,网络协议是连接世…...
PL/SQL编程
一、Oracle常用函数 concat:用于连接两个字符串。 CONCAT(Oraok, .com) -- Result: Oraok.com ceil:小数点向上取整。 secect ceil(7.3) from dual --Result: 8 dual表是oracle系统为计算设计的一张临时表 select sysdate as 系统日期 from dual…...

Prompt提示词——什么是CRISPE框架?QCIPSPE框架?
框架介绍 【CRISPE】框架 是由 Matt Nigh 提出并发布的提示词书写框架,共由五部分组成。 这个框架(CRISPE)主要包括五个部分,用于指导用户向ChatGPT提问。首先,通过设定ChatGPT的角色(Capacity and Role&…...

Nginx的核心配置文件
Nginx的核心配置文件 学习Nginx首先需要对它的核心配置文件有一定的认识,这个文件位于Nginx的安装目录/usr/local/nginx/conf目录下,名字为nginx.conf 详细配置,可以参考resources目录下的<<nginx配置中文详解.conf>> Nginx的核…...
)
Java,集合框架,关于Collection接口(子接口List和Set)
目录 数组储存多个数据方面的特点: Java集合框架体系:(Java.util包下) Collection接口中的方法测试: 迭代器(Iterator)的作用:用来遍历集合元素。 增强for循环(即for…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...
