【C刷题】day7
- 🎥 个人主页:深鱼~
- 🔥收录专栏:【C】每日一练
- 🌄欢迎 👍点赞✍评论⭐收藏
一、选择题
1、以下对C语言函数的有关描述中,正确的有【多选】( )
A: 在C语言中,一个函数一般由两个部分组成,它们是函数首部和函数体
B: 函数的实参和形参可以是相同的名字
C: 在main()中定义的变量都可以在其它被调函数中直接使用
D: 在C程序中,函数调用不能出现在表达式语句中
【答案】:
AB
【解析】:
考点:函数(局部变量+返回值+参数)
C:主函数中定义的局部变量只在主函数中有效,因为主函数也是一个函数,它与其他函数是平行关系,所以错误;
D:当函数有返回值时,可以出现在表达式中,所以错误
2、在C语言中,以下正确的说法是( )
A: 实参和与其对应的形参各占用独立的存储单元
B: 实参和与其对应的形参共占用一个存储单元
C: 只有当实参和与其对应的形参同名时才共占用存储单元
D: 形参是虚拟的,不占用存储单元
【答案】:
A
【解析】:
考点:形参和实参
A,B,C:形参是实参的一份临时拷贝,分别占用不同的内存空间
D:函数如果不被调用时,函数的形参是形式上存在的,但是函数在被调用的时候,形参是要分配内存空间的
3、在上下文及头文件均正常的情况下,下列代码的输出是( )(注: print 已经声明过)
int main()
{char str[] = "Geneius";print(str);return 0;
}
print(char *s)
{if(*s){print(++s);printf("%c", *s);}
}A: suiene B: neius C: run-time error D: suieneG
【答案】:
A
【解析】:
考点:递归的理解
递的过程:
*s=’G‘:++s,注意是先将s=s+1(s已经变了),再s+1的值赋给print函数
*s=’e‘:++s,先将s=s+1,再s+1的值赋给print函数
....
*s=’s‘:++s,先将s=s+1,再s+1的值赋给print函数
归的过程:
*s='\0':回到上一次递归
*s=’s‘:打印\0(因为s已经变成了当前字符的下一个),也就是不打印
...
*s=’e‘:打印n
*s=’G‘:打印e
代码实现了递归倒序打印字符串的功能,但是++s使得s的值发生了变化,回不到'G'的位置上,故而没有打印'G'
4、对于函数 void f(int x); ,下面调用正确的是( )
A: int y=f(9); B: f(9); C: f(f(9)); D: x=f();
【答案】:
B
【解析】:
考点:函数的返回值
A:函数f是没有返回值的,不能给int类型变量赋值,故错误同时需要一个整型参数,
C:f(9)不能作为f的参数,也是错的
D:没有传参,也不能接收返回值也是错误的
5、给定 fun 函数如下,那么 fun(10) 的输出结果是( )
int fun(int x)
{return (x==1) ? 1 : (x + fun(x-1));
}A: 0 B: 10 C: 55 D: 3628800
【答案】:
C
【解析】:
考点:递归的理解
x =10 :10+fun(9)
x =9:10+9+fun(8)
x = 8:10+9+8+fun(7)
...
x = 1:10+9+8+7+6+5+4+3+2+1
代码是一个递归函数,计算x+(x-1)+(x-2)+...+2+1即等差数列的和
二、编程题
1. 图片整理

【参考答案】:
思路:图片按照大小(ASCII码值从小到大)排列直接快排
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int char_cmp(const void* e1,const void*e2)
{return (*(char*)e1-*(char*)e2);
}
int main() {char str[1001]={0};while(~scanf("%s",str)){qsort(str, strlen(str), sizeof(char), char_cmp);printf("%s",str);}return 0;
}知识点补充:快排:
qsort函数是一个库函数,底层使用的快速排序的方式,对数据进行排序,这个函数可以直接使用,可以用来排序任意类型的数据
头文件:#include<stdlib.h>
void qsort( void *base, size_t num, size_t width, int (__cdecl *compare )(const void *elem1, const void *elem2 ) );
qsort(被排序数组的初始位置,要排序的数组的元素个数,一个元素所占字节,比较函数)
其中比较函数需要根据自己排序类型数据来写(以int类型快排为例)
int int_cmp(const void* e1, const void* e2)
{
return (*(int*)e1 - *(int*)e2);
}
如果想要更详细学习:可以看看这篇文章:【C进阶】指针(二)
2.寻找数组的中心下标

【参考答案】:
思路1:暴力求解:遍历数组i之前数之和为sum1,i之后的数之和为sum2,如果sum1等于sum2就返回1;否则返回-1
int pivotIndex(int* nums, int numsSize)
{for(int i=0;i<numsSize;i++){int sum1=0;int sum2=0;for(int j=0;j<i;j++){sum1+=nums[j];}for(int k=i+1;k<numsSize;k++){sum2+=nums[k];}if(sum1==sum2)return i;}return -1;
}思路2:先求出数组总和,然后遍历数组的过程中看当前sum的两倍加上当前元素值是否为数组总和,即:2*sum+nums[i]==total,等于就返回i,否则继续遍历,直到结束,如果结束还没有,就返回-1
int pivotIndex(int* nums, int numsSize)
{//计算总和int total=0;for(int i=0;i<numsSize;i++){total+=nums[i];}int sum=0;for(int i=0;i<numsSize;i++){if(2*sum+nums[i]==total)return i;sum+=nums[i];}return -1;
}相关文章:

【C刷题】day7
🎥 个人主页:深鱼~🔥收录专栏:【C】每日一练🌄欢迎 👍点赞✍评论⭐收藏 一、选择题 1、以下对C语言函数的有关描述中,正确的有【多选】( ) A: 在C语言中,一…...
数据挖掘复盘——apriori
read_csv函数返回的数据类型是Dataframe类型 对于Dataframe类型使用条件表达式 dfdf.loc[df.loc[:,0]2]df: 这是一个DataFrame对象的变量名,表示一个二维的表格型数据结构,类似于电子表格或SQL表。 df.loc[:, 0]: 这是使用DataFrame的.loc属性来进行…...

Windows10下Maven3.9.5安装教程
文章目录 1.下载maven2.安装3.配置系统变量3.1.新建系统变量 MAVEN_HOME3.2.编辑系统变量Path 4.CMD命令测试是否安装成功5.配置maven本地仓库6.配置国内镜像仓库 1.下载maven 官网 https://maven.apache.org/download.cgi 点击下载。 2.安装 解压到指定目录 D:\installSoft…...

【开源】基于JAVA的校园失物招领管理系统
项目编号: S 006 ,文末获取源码。 \color{red}{项目编号:S006,文末获取源码。} 项目编号:S006,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 招领管理模块2.2 寻物管理模块2.3 系…...

requests爬虫IP连接初始化问题及解决方案
问题背景 在使用HTTPS爬虫IP连接时,如果第一次请求是chunked方式,那么HTTPS爬虫IP连接将不会被初始化。这个问题可能会导致403错误,或者在使用HTTPS爬虫IP时出现SSL错误。 解决方案 为了解决这个问题,我们可以在requests库的ada…...
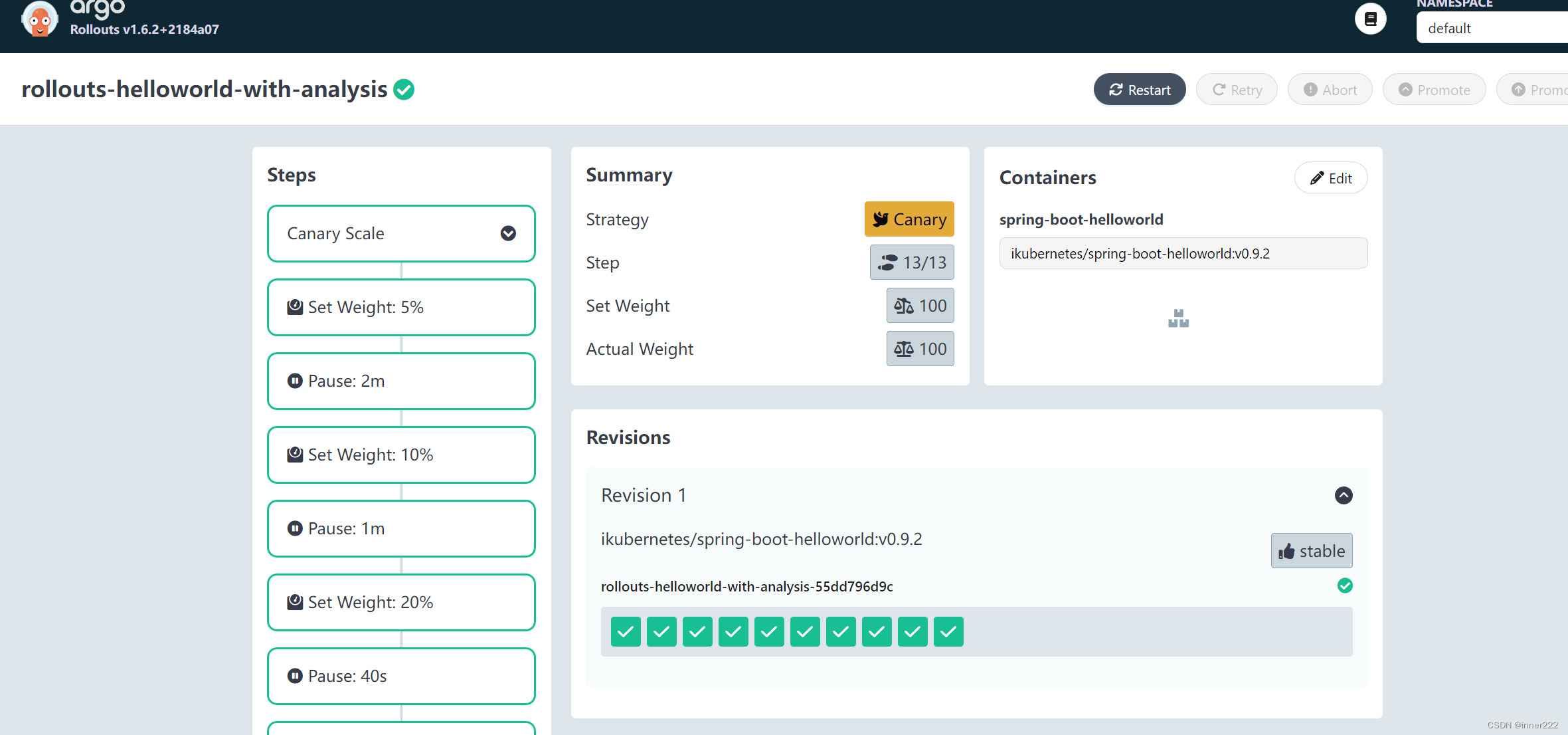
Argo Rollouts结合Service进行Blue-Green部署
删除03 部署04 rootk8s-master01:~/learning-jenkins-cicd/09-argocd-and-rollout/rollout-demos# kubectl delete -f 03-rollouts-with-prometheus-analysis.yaml rootk8s-master01:~/learning-jenkins-cicd/09-argocd-and-rollout/rollout-demos# kubectl apply -f 04-rol…...
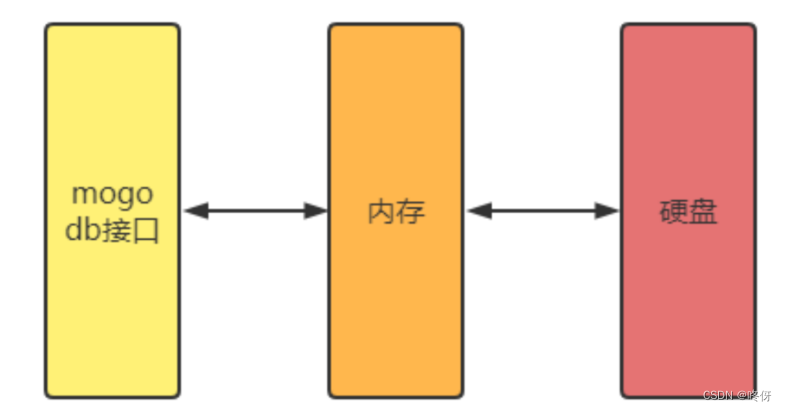
mongodb——原理简介,docker单机部署
MongoDB noSQL数据库 特点 数据文件存储格式为 BSON (JSON 的扩展) {“name”:“joe”}这是 BSON 的例子,其中"name"是键,"joe"是值。键值对组成了 BSON 格式。面向集合…...
ThinkPHP 系列漏洞
目录 2、thinkphp5 sql注入2 3、thinkphp5 sql注入3 4、 thinkphp5 SQL注入4 5、 thinkphp5 sql注入5 6、 thinkphp5 sql注入6 7、thinkphp5 文件包含漏洞 8、ThinkPHP5 RCE 1 9、ThinkPHP5 RCE 2 10、ThinkPHP5 rce3 11、ThinkPHP 5.0.X 反序列化漏洞 12、ThinkPHP…...

系列十、你说你做过JVM调优和参数配置,请问如何盘点JVM系统的默认值?
一、JVM的参数类型 1.1、标配参数 java -versionjava -help 1.2、XX参数 1.2.1、Boolean类型 公式:-XX:或者- 某个属性值 表示开启、-表示关闭 # 是否打印GC收集细节 -XX:PrintGCDetails -XX:-PrintGCDetails# 是否使用串行垃圾收集器 -XX:UseSerialGC -XX:-UseS…...
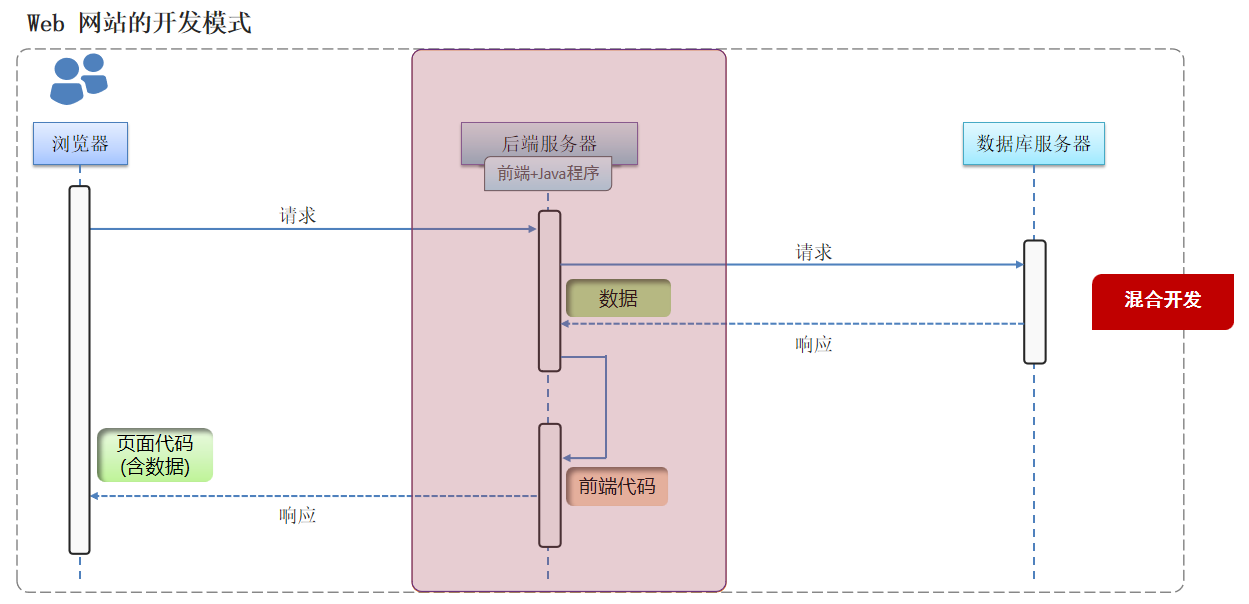
Java Web——Web开发介绍
什么是Web开发 Web开发是一种创建和维护全球广域网(World Wide Web)上的网站和应用的技术。全球广域网也称为万维网(www World Wide Web),是一个能够通过浏览器访问的互联网上的巨大信息库。 Web开发的目标是创建功能齐全、易于使用和安全的…...

Vue 数据监听机制及 Vue 2.0 和 Vue 3.0 的比较
Vue 数据监听机制 在 Vue 中,数据的变化通常是通过数据劫持(Data Binding)和观察者模式来实现的。当数据发生变化时,Vue 能够自动更新视图。 Vue 2.0 的数据监听 在 Vue 2.0 中,数据监听是通过 Object.defineProper…...

QT多线程项目中子线程无法修改主线程的ui组件
情况描述 今天我创建了一个QT多线程的工程,框架如下。我希望通过指针的方式,让子线程去直接修改主线程的ui组件,但事与愿违。 class ChildThread : public QThread {Q_OBJECT public:ChildThread (MainThread* par):m_Par(par){}; protecte…...
Python 如何实现备忘录设计模式?什么是备忘录设计模式?Python 备忘录设计模式示例代码
什么是备忘录(Memento)设计模式? 备忘录(Memento)设计模式是一种行为型设计模式,用于捕获一个对象的内部状态,并在对象之外保存这个状态,以便在需要时恢复对象到先前的状态。这种模…...
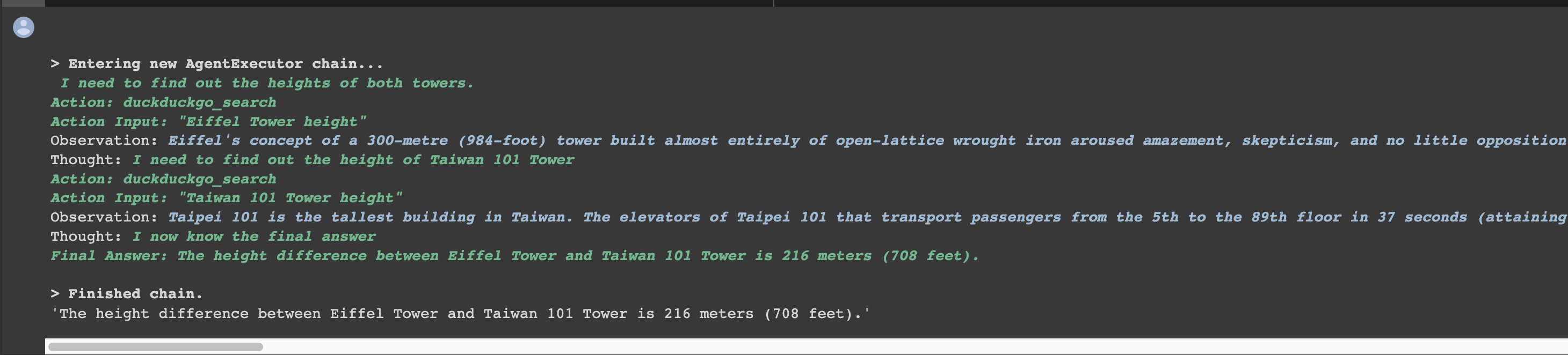
LangChain 代理 Agent(学习笔记)
原文:LangChain 代理 Agent(学习笔记) - 尘叶心繁的专栏 - TNBLOG LangChain 代理 Agent(学习笔记) LangChain 代理 Agent(学习笔记) 简介Agent Zero-shot ReActStructured Input ReActOpenAI FunctionsConversationalSelf ask with searchReAct document storePlan…...
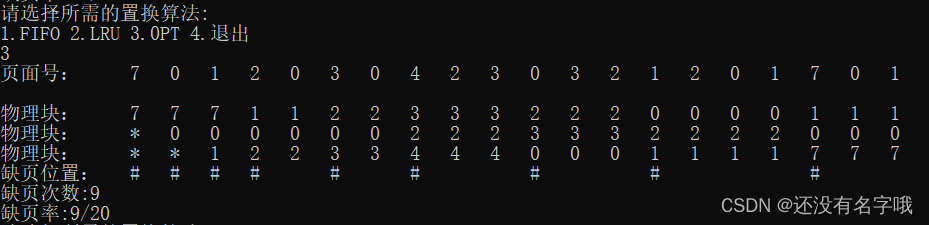
实验三 页面置换算法
一. 实验目的: 1、熟悉虚存管理的各种页面淘汰算法 二、实验环境: 硬件环境:计算机一台,局域网环境; 软件环境:Windows XP及以上版本 Professional操作系统平台,Visual C 6.0专业版或企业版…...

Node.js中的Buffer和Stream
Node.js中的Buffer和Stream 计算机只能理解二进制数据,即0和1形式的数据。这些数据的顺序移动称为流。以称为块(chunk)的破碎部分流式传输数据;计算机一收到数据块就开始处理数据,而不用等待整个数据。 我们这篇文章…...
3.5 Windows驱动开发:应用层与内核层内存映射
在上一篇博文《内核通过PEB得到进程参数》中我们通过使用KeStackAttachProcess附加进程的方式得到了该进程的PEB结构信息,本篇文章同样需要使用进程附加功能,但这次我们将实现一个更加有趣的功能,在某些情况下应用层与内核层需要共享一片内存…...

【小黑送书—第八期】>>别再吐槽大学教材了,来看看这些网友强推的数学神作!
导读:关于大学数学教材的吐槽似乎从来没停止过。有人慨叹:数学教材晦涩难懂。错!难懂,起码还可以读懂。数学教材你根本读不懂;也有人说:数学教材简直就是天书。 数学教材有好有坏,这话不假&…...
MatLab的下载、安装与使用(亲测有效)
1、概述 MatLab是由MathWorks公司开发并发布的,支持线性代数、矩阵运算、绘制函数和数据、信号处理、图像处理以及视频处理等功能。广泛用于算法开发、数据可视化、数据分析以及数值计算等。 Matlab 的主要特性包括: 简单易用的语法,使得程…...

无人智能货柜:引领便捷购物新体验
无人智能货柜:引领便捷购物新体验 无人智能货柜利用人工智能技术,将传统货架与电子商务相结合,形成智能销售终端。其采用先拿货后付款的购物模式,用户只需扫码、拿货、关门三个简洁流畅的步骤,极大地提升了消费者的购物…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
