15分钟,不,用模板做数据可视化只需5分钟
测试显示,一个对奥威BI软件不太熟悉的人来开发数据可视化报表,要15分钟,而当这个人去套用数据可视化模板做报表,只需5分钟!
数据可视化模板是奥威BI上的一个特色功能板块。用户下载后更新数据源,立即就能获得新报表,完成BI数据可视化分析。
数据可视化模板:所见即所得
你在模板秀中看到的数据可视化模板是什么样,下载套用后,它就是什么样,只一点,数据会变。套用前,模板里用的是虚拟数据;套用后,报表上分析展示的是用户自己的数据。
套用模板做分析,可个性化修改
修改的范围基本无限制,可对模板里的数据可视化图表、内存计算(分析指标计算)、智能分析功能(钻取、联动、筛选)以及图表样式做个性化的修改。
由于模板支持做任意修改,因此可以很好地满足不同分析场景下的数据分析需求。

模板封装成套,一经下载套用,立得系统化数据分析报表
奥威BI软件将不同主题的数据可视化模板集中起来,封装成套,形成多套系统化的BI数据可视化模板套装,且可无缝对接金蝶、用友主流ERP。
除此之外,还有数个行业的BI数据可视化模板套装,如BI零售数据分析套装里封装了“人、货、场、供、财“主题的BI数据可视化模型,重点关注零售数据分析关键指标、数据情况。比如在门店管理驾驶中集中分析展现人效、坪效、客单价、销售额等关键指标,又对商品品类结构、不同时间销售趋势等做了可视化的分析展现。
套用奥威BI的BI数据可视化模板,不仅报表做得快,数据分析地清楚,更能帮助业务人及时摸清数据的来龙去脉,排查问题原因,对解决问题、监控决策执行等起到了决定性作用。
相关文章:

15分钟,不,用模板做数据可视化只需5分钟
测试显示,一个对奥威BI软件不太熟悉的人来开发数据可视化报表,要15分钟,而当这个人去套用数据可视化模板做报表,只需5分钟! 数据可视化模板是奥威BI上的一个特色功能板块。用户下载后更新数据源,立即就能获…...

C 语言字符串函数
C 语言字符串函数 在本文中,您将学习使用诸如gets(),puts,strlen()等库函数在C中操作字符串。您将学习从用户那里获取字符串并对该字符串执行操作。 您通常需要根据问题的需要来操作字符串。大多数字符串操作都可以自定义方法完成ÿ…...
nvm安装详细教程(卸载旧的nodejs,安装nvm、node、npm、cnpm、yarn及环境变量配置)
文章目录 一、完全卸载旧的nodejs1、打开系统的控制面板,点击卸载程序,卸载nodejs(1)打开系统的控制面板,点击程序下的卸载程序(2)找到node.js,鼠标右击出现下拉框,点卸载…...
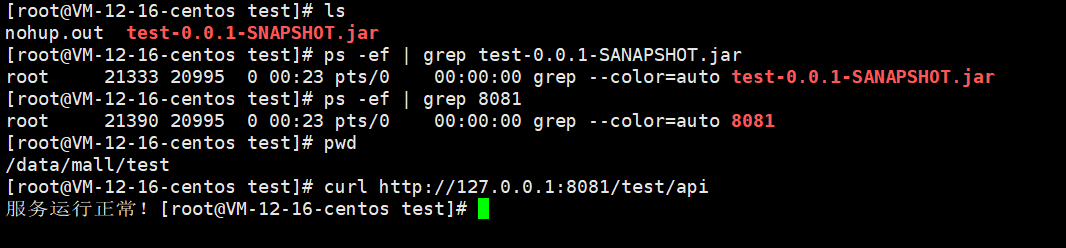
详细步骤记录:持续集成Jenkins自动化部署一个Maven项目
Jenkins自动化部署 提示:本教程基于CentOS Linux 7系统下进行 Jenkins的安装 1. 下载安装jdk11 官网下载地址:https://www.oracle.com/cn/java/technologies/javase/jdk11-archive-downloads.html 本文档教程选择的是jdk-11.0.20_linux-x64_bin.tar.g…...
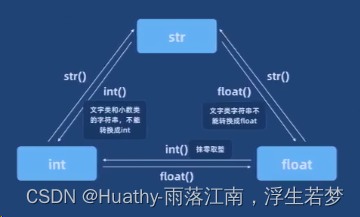
Python学习(一)基础语法
文章目录 1. 入门1.1 解释器的作用1.2 下载1.3 基础语法输入输出语法与引号注释:变量: 数据类型与四则运算数据类型四则运算数据类型的查看type()数据类型的转换int()、int()、float() 流程控制格式化输出循环与遍历逻辑运算符list遍历字典dict遍历 跳出…...

【C刷题】day7
🎥 个人主页:深鱼~🔥收录专栏:【C】每日一练🌄欢迎 👍点赞✍评论⭐收藏 一、选择题 1、以下对C语言函数的有关描述中,正确的有【多选】( ) A: 在C语言中,一…...
数据挖掘复盘——apriori
read_csv函数返回的数据类型是Dataframe类型 对于Dataframe类型使用条件表达式 dfdf.loc[df.loc[:,0]2]df: 这是一个DataFrame对象的变量名,表示一个二维的表格型数据结构,类似于电子表格或SQL表。 df.loc[:, 0]: 这是使用DataFrame的.loc属性来进行…...

Windows10下Maven3.9.5安装教程
文章目录 1.下载maven2.安装3.配置系统变量3.1.新建系统变量 MAVEN_HOME3.2.编辑系统变量Path 4.CMD命令测试是否安装成功5.配置maven本地仓库6.配置国内镜像仓库 1.下载maven 官网 https://maven.apache.org/download.cgi 点击下载。 2.安装 解压到指定目录 D:\installSoft…...

【开源】基于JAVA的校园失物招领管理系统
项目编号: S 006 ,文末获取源码。 \color{red}{项目编号:S006,文末获取源码。} 项目编号:S006,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 招领管理模块2.2 寻物管理模块2.3 系…...

requests爬虫IP连接初始化问题及解决方案
问题背景 在使用HTTPS爬虫IP连接时,如果第一次请求是chunked方式,那么HTTPS爬虫IP连接将不会被初始化。这个问题可能会导致403错误,或者在使用HTTPS爬虫IP时出现SSL错误。 解决方案 为了解决这个问题,我们可以在requests库的ada…...
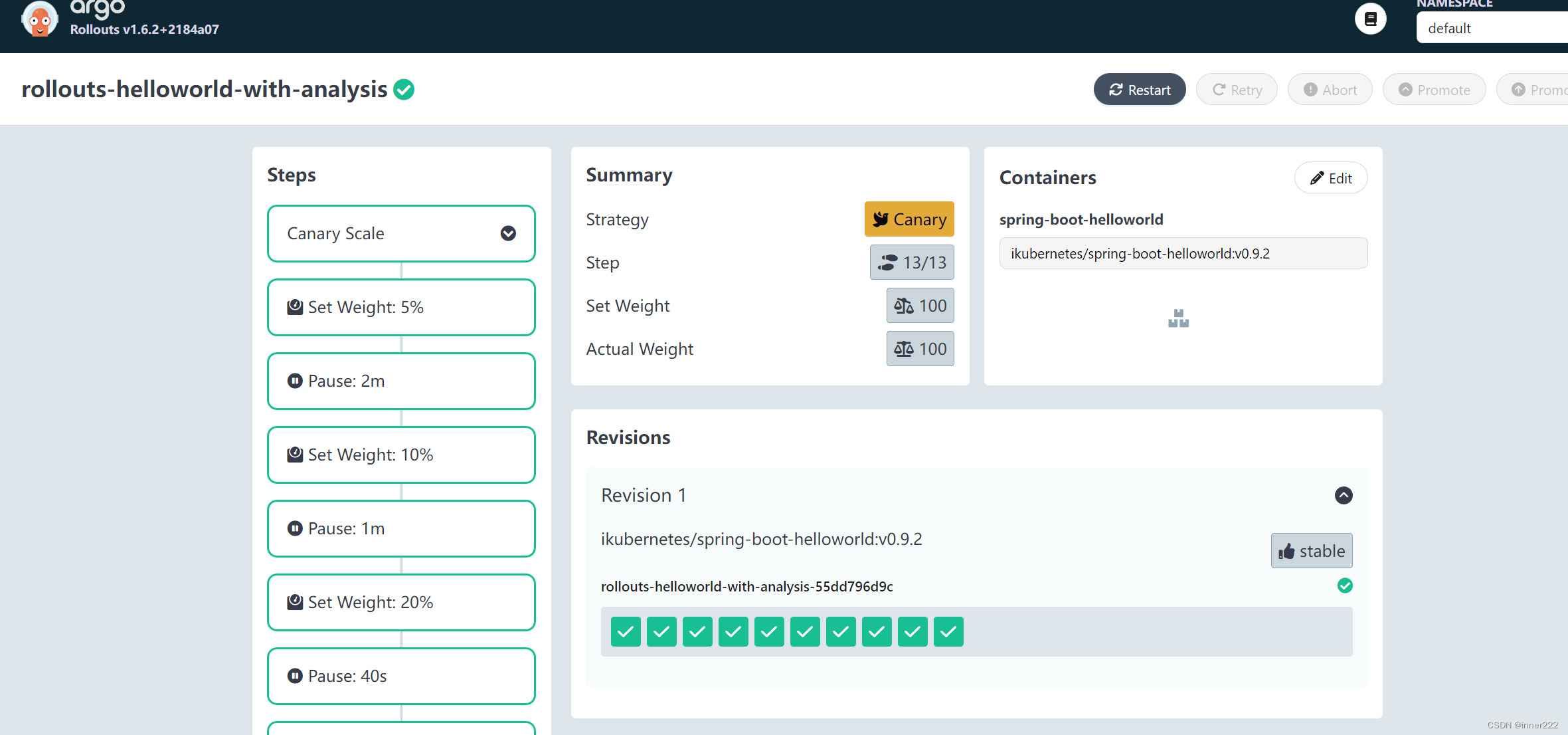
Argo Rollouts结合Service进行Blue-Green部署
删除03 部署04 rootk8s-master01:~/learning-jenkins-cicd/09-argocd-and-rollout/rollout-demos# kubectl delete -f 03-rollouts-with-prometheus-analysis.yaml rootk8s-master01:~/learning-jenkins-cicd/09-argocd-and-rollout/rollout-demos# kubectl apply -f 04-rol…...
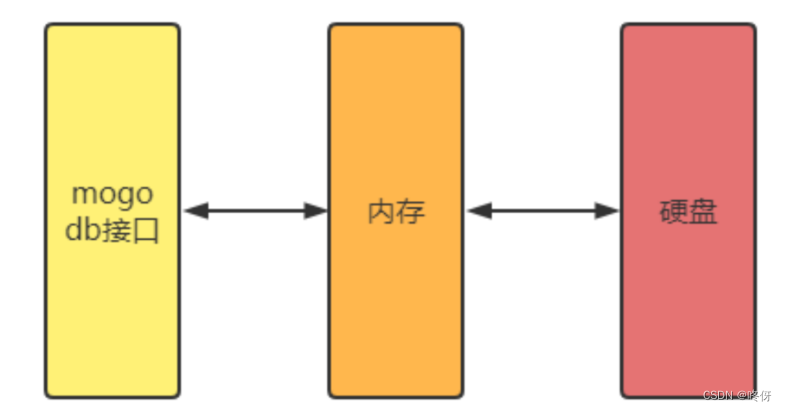
mongodb——原理简介,docker单机部署
MongoDB noSQL数据库 特点 数据文件存储格式为 BSON (JSON 的扩展) {“name”:“joe”}这是 BSON 的例子,其中"name"是键,"joe"是值。键值对组成了 BSON 格式。面向集合…...
ThinkPHP 系列漏洞
目录 2、thinkphp5 sql注入2 3、thinkphp5 sql注入3 4、 thinkphp5 SQL注入4 5、 thinkphp5 sql注入5 6、 thinkphp5 sql注入6 7、thinkphp5 文件包含漏洞 8、ThinkPHP5 RCE 1 9、ThinkPHP5 RCE 2 10、ThinkPHP5 rce3 11、ThinkPHP 5.0.X 反序列化漏洞 12、ThinkPHP…...

系列十、你说你做过JVM调优和参数配置,请问如何盘点JVM系统的默认值?
一、JVM的参数类型 1.1、标配参数 java -versionjava -help 1.2、XX参数 1.2.1、Boolean类型 公式:-XX:或者- 某个属性值 表示开启、-表示关闭 # 是否打印GC收集细节 -XX:PrintGCDetails -XX:-PrintGCDetails# 是否使用串行垃圾收集器 -XX:UseSerialGC -XX:-UseS…...
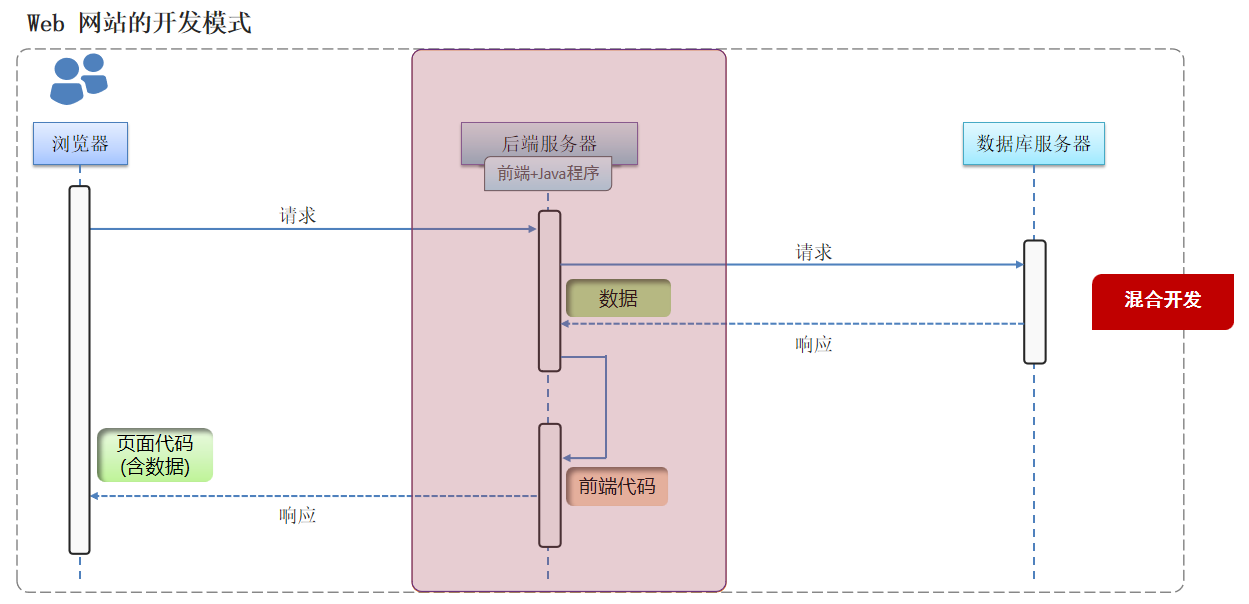
Java Web——Web开发介绍
什么是Web开发 Web开发是一种创建和维护全球广域网(World Wide Web)上的网站和应用的技术。全球广域网也称为万维网(www World Wide Web),是一个能够通过浏览器访问的互联网上的巨大信息库。 Web开发的目标是创建功能齐全、易于使用和安全的…...

Vue 数据监听机制及 Vue 2.0 和 Vue 3.0 的比较
Vue 数据监听机制 在 Vue 中,数据的变化通常是通过数据劫持(Data Binding)和观察者模式来实现的。当数据发生变化时,Vue 能够自动更新视图。 Vue 2.0 的数据监听 在 Vue 2.0 中,数据监听是通过 Object.defineProper…...

QT多线程项目中子线程无法修改主线程的ui组件
情况描述 今天我创建了一个QT多线程的工程,框架如下。我希望通过指针的方式,让子线程去直接修改主线程的ui组件,但事与愿违。 class ChildThread : public QThread {Q_OBJECT public:ChildThread (MainThread* par):m_Par(par){}; protecte…...
Python 如何实现备忘录设计模式?什么是备忘录设计模式?Python 备忘录设计模式示例代码
什么是备忘录(Memento)设计模式? 备忘录(Memento)设计模式是一种行为型设计模式,用于捕获一个对象的内部状态,并在对象之外保存这个状态,以便在需要时恢复对象到先前的状态。这种模…...
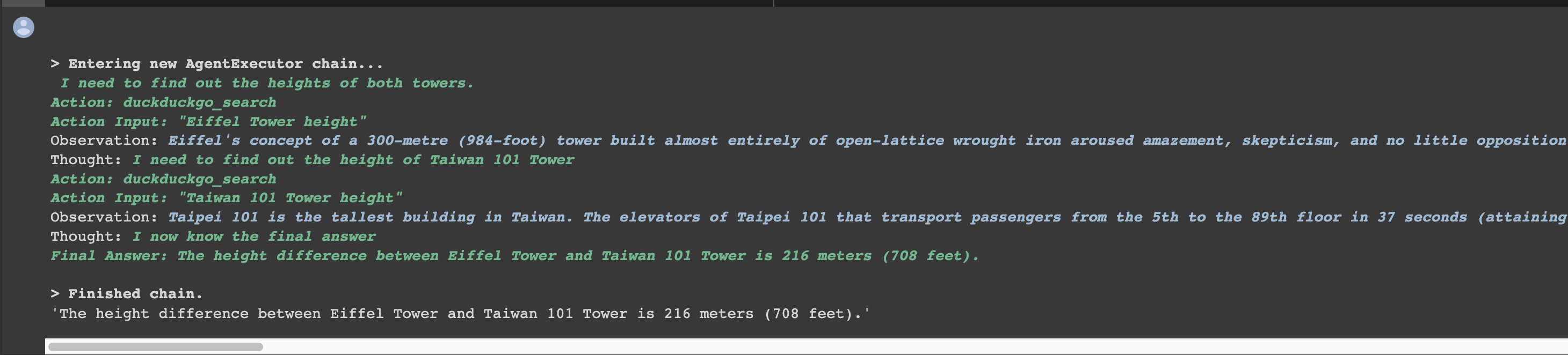
LangChain 代理 Agent(学习笔记)
原文:LangChain 代理 Agent(学习笔记) - 尘叶心繁的专栏 - TNBLOG LangChain 代理 Agent(学习笔记) LangChain 代理 Agent(学习笔记) 简介Agent Zero-shot ReActStructured Input ReActOpenAI FunctionsConversationalSelf ask with searchReAct document storePlan…...
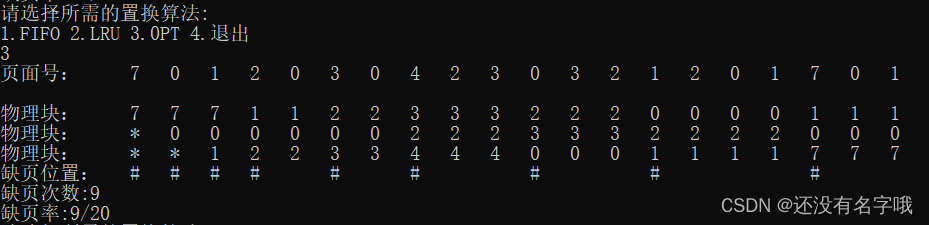
实验三 页面置换算法
一. 实验目的: 1、熟悉虚存管理的各种页面淘汰算法 二、实验环境: 硬件环境:计算机一台,局域网环境; 软件环境:Windows XP及以上版本 Professional操作系统平台,Visual C 6.0专业版或企业版…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
