矩阵的QR分解
矩阵的QR分解
GramSchmidt
设存在 B = { x 1 , x 2 , … , x n } \mathcal{B}=\left\{\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}\right\} B={x1,x2,…,xn}在施密特正交化过程中
- q 1 = x 1 ∣ ∣ x 1 ∣ ∣ q_1=\frac{x_1}{||x_1||} q1=∣∣x1∣∣x1
- q k = x k − ∑ i = 1 k − 1 < q i , x k > u i ∣ ∣ x k − ∑ i = 1 k − 1 < q i , x k > u i ∣ ∣ q_k=\frac{x_k-\sum_{i=1}^{k-1}\left< q_i,x_k\right>u_i}{||x_k-\sum_{i=1}^{k-1}\left< q_i,x_k\right>u_i||} qk=∣∣xk−∑i=1k−1⟨qi,xk⟩ui∣∣xk−∑i=1k−1⟨qi,xk⟩ui
对于任意一个矩阵 A m × n = { a 1 ∣ a 2 ∣ … ∣ a n } A_{m\times n}=\{a_1|a_2|\dots|a_n\} Am×n={a1∣a2∣…∣an},其行向量线性无关,则存在 A = Q R A=QR A=QR,其 Q m × n = { q 1 ∣ q 2 ∣ … ∣ q n } Q_{m\times n}=\{q_1|q_2|\dots|q_n\} Qm×n={q1∣q2∣…∣qn}矩阵是 R ( A ) R(A) R(A)的一组正交基, R m × m R_{m\times m} Rm×m是一个上三角矩阵,则
R = ( ν 1 q 1 ∗ a 2 q 1 ∗ a 3 ⋯ q 1 ∗ a n 0 ν 2 q 2 ∗ a 3 ⋯ q 2 ∗ a n 0 0 ν 3 ⋯ q 3 ∗ a n ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ ν n ) \mathbf{R}=\begin{pmatrix}\nu_1&\mathbf{q}_1^*\mathbf{a}_2&\mathbf{q}_1^*\mathbf{a}_3&\cdots&\mathbf{q}_1^*\mathbf{a}_n\\0&\nu_2&\mathbf{q}_2^*\mathbf{a}_3&\cdots&\mathbf{q}_2^*\mathbf{a}_n\\0&0&\nu_3&\cdots&\mathbf{q}_3^*\mathbf{a}_n\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&\nu_n\end{pmatrix} R= ν100⋮0q1∗a2ν20⋮0q1∗a3q2∗a3ν3⋮0⋯⋯⋯⋱⋯q1∗anq2∗anq3∗an⋮νn
其中 v 1 = ∣ ∣ a 1 ∣ ∣ , v k = ∣ ∣ a k − ∑ i = 1 k − 1 < q i , a k > q i ∣ ∣ for k>1 v_1=||a_1||,v_k=||a_k-\sum_{i=1}^{k-1}<q_i,a_k>q_i|| \quad\text{for k>1} v1=∣∣a1∣∣,vk=∣∣ak−∑i=1k−1<qi,ak>qi∣∣for k>1

Householder
酉矩阵:一个复数矩阵 U n × n U_{n\times n} Un×n它的行或列构成一个 C n C^n Cn的正交基,其中 U ∗ U = I , ∣ ∣ U x ∣ ∣ 2 = ∣ ∣ x ∣ ∣ 2 U^*U=I,||Ux||_2=||x||_2 U∗U=I,∣∣Ux∣∣2=∣∣x∣∣2
对于非0向量 U ∈ C n × 1 U \in C^{n\times 1} U∈Cn×1 ,则 U U U的正交投影是 P u = U U ∗ U ∗ U P_u=\frac{UU^*}{U^*U} Pu=U∗UUU∗,其垂直方向的投影是 P u ⊥ = I − U U ∗ U ∗ U P_{u\perp}=I-\frac{UU^*}{U^*U} Pu⊥=I−U∗UUU∗
初等反射( householder 变换)
其中对于 u ⊥ u^{\perp} u⊥ 的初等反射为 R = I − 2 U U ∗ U ∗ U R=I-2\frac{UU^*}{U^*U} R=I−2U∗UUU∗
对于矩阵 A m × n = [ A ∗ 1 ∣ A ∗ 2 ∣ ⋯ ∣ A ∗ n ] \mathbf{A}_{m\times n}=[\mathbf{A}_{*1}|\mathbf{A}_{*2}|\cdots|\mathbf{A}_{*n}] Am×n=[A∗1∣A∗2∣⋯∣A∗n]
构建基本反射 R = I − 2 U U ∗ U ∗ U R=I-2\frac{UU^*}{U^*U} R=I−2U∗UUU∗,其中 u = A ∗ 1 ± μ ∣ ∣ A ∗ 1 ∣ ∣ e 1 , μ = { 1 if x 1 is real , x 1 / ∣ x 1 ∣ if x 1 is not real , u=A_{*1}\pm\mu||A_{*1}||e_1,\quad\left.\mu=\left\{\begin{matrix}1&\text{if }x_1\text{ is real},\\x_1/|x_1|&\text{if }x_1\text{ is not real},\end{matrix}\right.\right. u=A∗1±μ∣∣A∗1∣∣e1,μ={1x1/∣x1∣if x1 is real,if x1 is not real,
根据householder变换可得 R 1 A ∗ 1 = ∓ μ ∥ A ∗ 1 ∥ e 1 = ( t 11 , 0 , ⋯ , 0 ) T \mathbf{R}_1\mathbf{A}_{*1}=\mp\mu\|\mathbf{A}_{*1}\|\mathbf{e}_1=(t_{11},0,\cdots,0)^T R1A∗1=∓μ∥A∗1∥e1=(t11,0,⋯,0)T
所以 R 1 A = [ R 1 A ∗ 1 ∣ R 1 A ∗ 2 ∣ ⋯ ∣ R 1 A ∗ n ] = ( t 11 t 1 T 0 A 2 ) \left.\mathbf{R}_1\mathbf{A}=[\mathbf{R}_1\mathbf{A}_{*1}|\mathbf{R}_1\mathbf{A}_{*2}|\cdots|\mathbf{R}_1\mathbf{A}_{*n}]=\left(\begin{array}{cc}t_{11}&\mathbf{t}_1^T\\\mathbf{0}&\mathbf{A}_2\end{array}\right.\right) R1A=[R1A∗1∣R1A∗2∣⋯∣R1A∗n]=(t110t1TA2),其中 A 2 A_2 A2 是一个 ( m − 1 × n − 1 ) (m-1\times n-1) (m−1×n−1)的矩阵
若同时对 A 2 A_2 A2矩阵进行操作可以得到一个上三角矩阵 ( m = n ) (m=n) (m=n),即 P A = T PA=T PA=T,其中 P P P矩阵为elementary reflector矩阵的乘积, T T T矩阵为上梯形


Givens 旋转

对于正交矩阵 P P P形式如上,表示在平面 ( i , j ) (i,j) (i,j)上旋转,其中 s 2 + c 2 = 1 s^2+c^2=1 s2+c2=1
对于向量 X = { x 1 , x 2 … , x n } T X=\{x_1,x_2\dots,x_n\}^T X={x1,x2…,xn}T, P i j X = { x 1 , x 2 , … , c x i + s x j , … , − s x i + c x j , … , x n } T P_{ij}X=\{x_1,x_2,\dots,cx_i+sx_j,\dots,-sx_i+cx_j,\dots,x_n\}^T PijX={x1,x2,…,cxi+sxj,…,−sxi+cxj,…,xn}T,易知旋转矩阵乘某一个向量,其只有在该旋转平面上的值发生改变,若存在:
c = x i x i 2 + x j 2 , s = x j x i 2 + x j 2 c=\frac{x_i}{\sqrt{x_i^2+x_j^2}},s=\frac{x_j}{\sqrt{x_i^2+x_j^2}} c=xi2+xj2xi,s=xi2+xj2xj
则 P i j X = { x 1 , x 2 , … , x i 2 + x j 2 , … , 0 , … , x n } T P_{ij}X=\{x_1,x_2,\dots,\sqrt{x_i^2+x_j^2},\dots,0,\dots,x_n\}^T PijX={x1,x2,…,xi2+xj2,…,0,…,xn}T
由此可以实现消去向量的第j个值,即存在:
P 12 x = ( x 1 2 + x 2 2 0 x 3 x 4 ⋮ x n ) , P 13 P 12 x = ( x 1 2 + x 2 2 + x 3 2 0 x 4 ⋮ x n ) , … , P 1 n ⋯ P 13 P 12 x = ( ∥ x ∥ 0 0 ⋮ 0 ) . \mathbf P_{12}\mathbf x=\begin{pmatrix}\sqrt{x_1^2+x_2^2}\\0\\x_3\\x_4\\\vdots\\x_n\end{pmatrix},~\mathbf P_{13}\mathbf P_{12}\mathbf x=\begin{pmatrix}\sqrt{x_1^2+x_2^2+x_3^2}\\0\\x_4\\\vdots\\x_n\end{pmatrix},~\ldots,~\mathbf P_{1n}\cdots\mathbf P_{13}\mathbf P_{12}\mathbf x=\begin{pmatrix}\|\mathbf x\|\\0\\0\\\vdots\\0\end{pmatrix}. P12x= x12+x220x3x4⋮xn , P13P12x= x12+x22+x320x4⋮xn , …, P1n⋯P13P12x= ∥x∥00⋮0 .
若 A A A矩阵是非奇异矩阵,则可以利用householder、givens以及Gram-schmidt来产生一个正交矩阵 Q Q Q以及一个上三角矩阵 R R R其对角线上全为正数,可以得到形如 A = Q R A=QR A=QR的形式
相关文章:

矩阵的QR分解
矩阵的QR分解 GramSchmidt 设存在 B { x 1 , x 2 , … , x n } \mathcal{B}\left\{\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}\right\} B{x1,x2,…,xn}在施密特正交化过程中 q 1 x 1 ∣ ∣ x 1 ∣ ∣ q_1\frac{x_1}{||x_1||} q1∣∣x1∣∣x1 q k …...

STL总结
STL vector 头文件<vector> 初始化,定义,定义长度,定义长度并且赋值,从数组中获取数据返回元素个数size()判断是否为空empty()返回第一个元素front()返回最后一个数back()删除最后一个数pop_back()插入push_back(x)清空clear()begin()end()使用s…...
资深测试总结,现在软件测试有未来吗?“你“的底气在哪里?
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、为什么会有 “…...

Scalable Exact Inference in Multi-Output Gaussian Processes
Orthogonal Instantaneous Linear Mixing Model TY are m-dimensional summaries,ILMM means ‘Instantaneous Linear Mixing Model’,OILMM means ‘Orthogonal Instantaneous Linear Mixing Model’ 辅助信息 作者未提供代码...
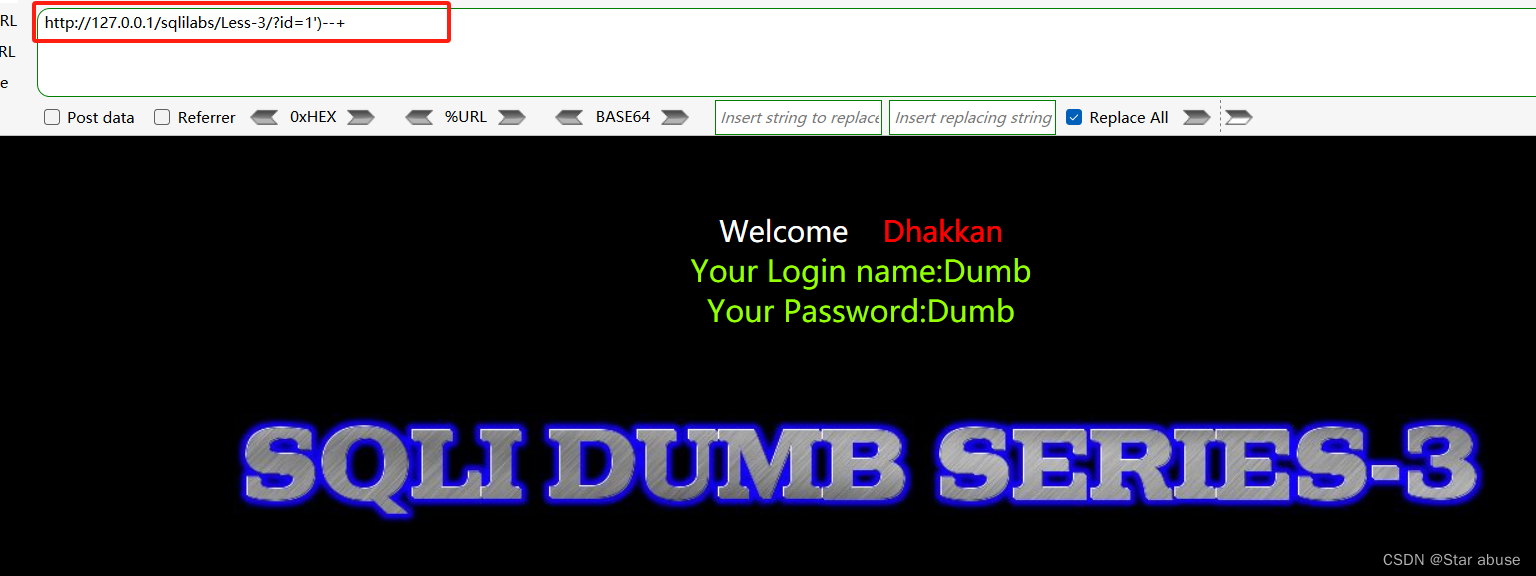
sqli-labs(Less-3)
1. 通过构造id1’ 和id1’) 和id1’)–确定存在注入 可知原始url为 id(‘1’) 2.使用order by 语句猜字段数 http://127.0.0.1/sqlilabs/Less-3/?id1) order by 4 -- http://127.0.0.1/sqlilabs/Less-3/?id1) order by 3 --3. 使用联合查询union select http://127.0.0.1…...

集合框架面试题
一、集合容器的概述 1. 什么是集合 集合框架:用于存储数据的容器。 集合框架是为表示和操作集合而规定的一种统一的标准的体系结构。 任何集合框架都包含三大块内容: 对外的接口、接口的实现和对集合运算的算 法。 接口:表示集合的抽象数据…...

【LeetCode刷题日志】225.用队列实现栈
🎈个人主页:库库的里昂 🎐C/C领域新星创作者 🎉欢迎 👍点赞✍评论⭐收藏✨收录专栏:LeetCode 刷题日志🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,…...

【JavaScript】fetch 处理流式数据,实现类 chatgpt 对话
本文只包含最基础的请求后端大佬给得对话接口,大部分模型的传参是差不多的,核心还是如何处理 fetch 获取的流数据 import { defineStore } from pinia; import { ElMessage } from element-plus;type Role system | user | assistant; export interfac…...

收发电子邮件
电子邮件是Internet提供的又一个重要服务项目。早在1987年9月20日,中国首封电子邮件就是从北京经意大利向前联邦德国卡尔斯鲁厄大学发出的,在中国首次实现了与Internet的连接,使中国成为国际互联网大家庭中的一员。现在随着Internet的迅速发展…...
)
sql13(Leetcode570至少有5名直接下属的经理)
代码: 脑子记不住 语法全靠试.. # Write your MySQL query statement below select b.name from (select managerId,count(managerId) as numfrom Employeegroup by managerId ) a left join Employee b on a.managerIdb.id where a.num>5 and b.name is not N…...

15分钟,不,用模板做数据可视化只需5分钟
测试显示,一个对奥威BI软件不太熟悉的人来开发数据可视化报表,要15分钟,而当这个人去套用数据可视化模板做报表,只需5分钟! 数据可视化模板是奥威BI上的一个特色功能板块。用户下载后更新数据源,立即就能获…...

C 语言字符串函数
C 语言字符串函数 在本文中,您将学习使用诸如gets(),puts,strlen()等库函数在C中操作字符串。您将学习从用户那里获取字符串并对该字符串执行操作。 您通常需要根据问题的需要来操作字符串。大多数字符串操作都可以自定义方法完成ÿ…...
nvm安装详细教程(卸载旧的nodejs,安装nvm、node、npm、cnpm、yarn及环境变量配置)
文章目录 一、完全卸载旧的nodejs1、打开系统的控制面板,点击卸载程序,卸载nodejs(1)打开系统的控制面板,点击程序下的卸载程序(2)找到node.js,鼠标右击出现下拉框,点卸载…...
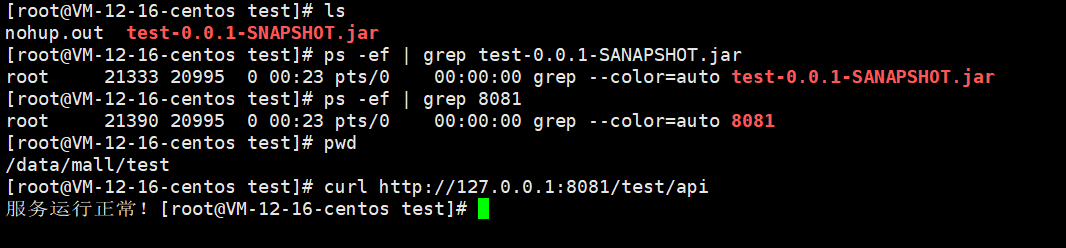
详细步骤记录:持续集成Jenkins自动化部署一个Maven项目
Jenkins自动化部署 提示:本教程基于CentOS Linux 7系统下进行 Jenkins的安装 1. 下载安装jdk11 官网下载地址:https://www.oracle.com/cn/java/technologies/javase/jdk11-archive-downloads.html 本文档教程选择的是jdk-11.0.20_linux-x64_bin.tar.g…...
Python学习(一)基础语法
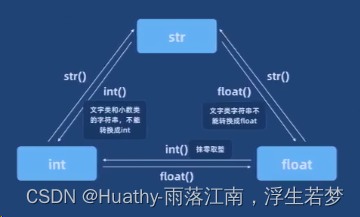
文章目录 1. 入门1.1 解释器的作用1.2 下载1.3 基础语法输入输出语法与引号注释:变量: 数据类型与四则运算数据类型四则运算数据类型的查看type()数据类型的转换int()、int()、float() 流程控制格式化输出循环与遍历逻辑运算符list遍历字典dict遍历 跳出…...

【C刷题】day7
🎥 个人主页:深鱼~🔥收录专栏:【C】每日一练🌄欢迎 👍点赞✍评论⭐收藏 一、选择题 1、以下对C语言函数的有关描述中,正确的有【多选】( ) A: 在C语言中,一…...
数据挖掘复盘——apriori
read_csv函数返回的数据类型是Dataframe类型 对于Dataframe类型使用条件表达式 dfdf.loc[df.loc[:,0]2]df: 这是一个DataFrame对象的变量名,表示一个二维的表格型数据结构,类似于电子表格或SQL表。 df.loc[:, 0]: 这是使用DataFrame的.loc属性来进行…...

Windows10下Maven3.9.5安装教程
文章目录 1.下载maven2.安装3.配置系统变量3.1.新建系统变量 MAVEN_HOME3.2.编辑系统变量Path 4.CMD命令测试是否安装成功5.配置maven本地仓库6.配置国内镜像仓库 1.下载maven 官网 https://maven.apache.org/download.cgi 点击下载。 2.安装 解压到指定目录 D:\installSoft…...

【开源】基于JAVA的校园失物招领管理系统
项目编号: S 006 ,文末获取源码。 \color{red}{项目编号:S006,文末获取源码。} 项目编号:S006,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 招领管理模块2.2 寻物管理模块2.3 系…...

requests爬虫IP连接初始化问题及解决方案
问题背景 在使用HTTPS爬虫IP连接时,如果第一次请求是chunked方式,那么HTTPS爬虫IP连接将不会被初始化。这个问题可能会导致403错误,或者在使用HTTPS爬虫IP时出现SSL错误。 解决方案 为了解决这个问题,我们可以在requests库的ada…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
