LeeCode AutoX-4 计算几何
题意
传送门 LeeCode AutoX-4 蚂蚁爬行
题解
枚举每一对几何图形,判断相交性,用并查集维护连通性即可。总时间复杂度 O ( n 2 + m ) O(n^2 + m) O(n2+m),其中 n n n 为几何图形数量, m m m 为查询数量。
根据几何图形性质分类讨论。
判断两圆相交,令 d d d 表示圆心距离, r 1 , r 2 ( r 1 ≤ r 2 ) r1,r2(r1\leq r2) r1,r2(r1≤r2) 分别为两圆半径,则充要条件为 r 2 − r 1 ≤ d ≤ r 1 + r 2 r2 - r1 \leq d \leq r1 + r2 r2−r1≤d≤r1+r2。
判断两线段相交,一类思路是计算出交点,在判断交点是否处于两条线段上;由于只用判断相交性,不用求交点,可以使用基于ccw函数的做法简单求解,具体而言,用端点表示的两条非平行的线段 ( p 1 , p 2 ) , ( q 1 , q 2 ) (p1,p2),(q1,q2) (p1,p2),(q1,q2),对其中任意线段 ( p 1 , p 2 ) (p1, p2) (p1,p2) 而言,另一条线段 ( q 1 , q 2 ) (q1, q2) (q1,q2) 的两个端点必然在 ( p 1 , p 2 ) (p1, p2) (p1,p2) 所在直线的两侧(或者至多一个端点位于直线上),此时可以通过叉积简单地进行判断。
判断线段与圆的相交性,若圆心到线段所在直线的最小距离大于半径,则不可能相交;反之,若线段存在位于圆上的端点,则相交;若线段存在位于圆内部的端点,则除了两个端点都位于圆内的情况,其他情况都相交;其余情况,圆心与线段两端点的连线都位于圆心与线段的垂线两侧,此时可以通过内积简单地进行判断。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using lll = __int128;
struct Point {ll x, y;Point operator+(Point o) {return {x + o.x, y + o.y};}Point operator-(Point o) {return {x - o.x, y - o.y};}ll dot(Point o) {return x * o.x + y * o.y;}ll det(Point o) {return x * o.y - o.x * y;}
};
struct DSU {vector<int> par;DSU(int n) : par(n) {iota(par.begin(), par.end(), 0);}int find(int x) {return par[x] == x ? x : (par[x] = find(par[x]));}void unite(int x, int y) {x = find(x), y = find(y);par[x] = y;}bool same(int x, int y) {return find(x) == find(y);}
};
class Solution {public:vector<bool> antPass(vector<vector<int>> &geometry, vector<vector<int>> &path) {int n = geometry.size();DSU dsu(n);auto on_seg = [&](Point &p, Point &q1, Point &q2) {return (q1 - p).det(q2 - p) == 0 && (q1 - p).dot(q2 - p) <= 0;};auto intersection = [&](Point &p1, Point &p2, Point &q1, Point &q2) {auto f = [&](Point &p1, Point &p2, Point &q1, Point &q2) {return (lll)(p1 - p2).det(q1 - p2) * (p1 - p2).det(q2 - p2) <= 0;};if ((p1 - p2).det(q1 - q2) == 0) {return on_seg(p1, q1, q2) || on_seg(p2, q1, q2) || on_seg(q1, p1, p2) || on_seg(q2, p1, p2);}return f(p1, p2, q1, q2) && f(q1, q2, p1, p2);};auto in_circle = [&](Point p, Point q, ll r) {return (p - q).dot(p - q) < r * r;};auto on_circle = [&](Point p, Point q, ll r) {return (p - q).dot(p - q) == r * r;};for (int i = 0; i < n; ++i) {for (int j = 0; j < i; ++j) {int n = geometry[i].size(), m = geometry[j].size();if (n == m) {if (n == 3) {ll dx = geometry[i][0] - geometry[j][0];ll dy = geometry[i][1] - geometry[j][1];ll r = geometry[i][2] + geometry[j][2];ll l = max(geometry[i][2], geometry[j][2]) - min(geometry[i][2], geometry[j][2]);if (dx * dx + dy * dy <= r * r && dx * dx + dy * dy >= l * l) {dsu.unite(i, j);}} else {Point p1 = {geometry[i][0], geometry[i][1]};Point p2 = {geometry[i][2], geometry[i][3]};Point q1 = {geometry[j][0], geometry[j][1]};Point q2 = {geometry[j][2], geometry[j][3]};if (intersection(p1, p2, q1, q2)) {dsu.unite(i, j);}}} else {auto a = geometry[i], b = geometry[j];if (a.size() == 3) {swap(a, b);}Point p1 = {a[0], a[1]};Point p2 = {a[2], a[3]};Point q = {b[0], b[1]};ll r = b[2];lll d = (p1 - p2).det(p1 - q);if (d * d <= (lll)(p1 - p2).dot(p1 - p2) * r * r) {int can = 0;if (on_circle(p1, q, r) || on_circle(p2, q, r)) {can = 1;} else if (in_circle(p1, q, r) || in_circle(p2, q, r)) {can = !(in_circle(p1, q, r) && in_circle(p2, q, r));} else if (((p1 - q).dot(p1 - p2) > 0) != ((p2 - q).dot(p1 - p2) > 0)) {can = 1;}if (can) {dsu.unite(i, j);}}}}}int m = path.size();vector<bool> res(m);for (int i = 0; i < m; ++i) {res[i] = dsu.same(path[i][0], path[i][1]);}return res;}
};
相关文章:

LeeCode AutoX-4 计算几何
题意 传送门 LeeCode AutoX-4 蚂蚁爬行 题解 枚举每一对几何图形,判断相交性,用并查集维护连通性即可。总时间复杂度 O ( n 2 m ) O(n^2 m) O(n2m),其中 n n n 为几何图形数量, m m m 为查询数量。 根据几何图形性质分类讨…...

Vue3 动态设置 ref
介绍 在一些场景,ref设置是未知的需要根据动态数据来决定,如表格中的input框需要我们主动聚焦,就需要给每一个input设置一个ref,进而进行聚焦操作。 Demo 点击下面截图中的编辑按钮,自动聚焦到相应的输入框中。 &…...

fast lio 2 保存每一帧的点云PCD和里程计矩阵 Odom 在txt文件
修改了源代码的 laserMapping.cpp 文件,替换为下面的代码就可以保存了,注意里面有一个路径,需要修改为你的电脑的路径 // This is an advanced implementation of the algorithm described in the // following paper: // J. Zhang and S. Singh. LOAM: Lidar Odometry an…...

当前主流DDos方式有哪几类
随着互联网的普及和技术的进步,网络安全问题日益凸显。DDoS攻击作为其中一种常见且具破坏性的攻击方式,受到了广泛关注。小德将带领大家一起来了解当前流行的三种DDoS攻击方式。 1. 容量耗尽攻击 容量耗尽攻击是最常见也是最直接的DDoS攻击方式。攻击者通…...
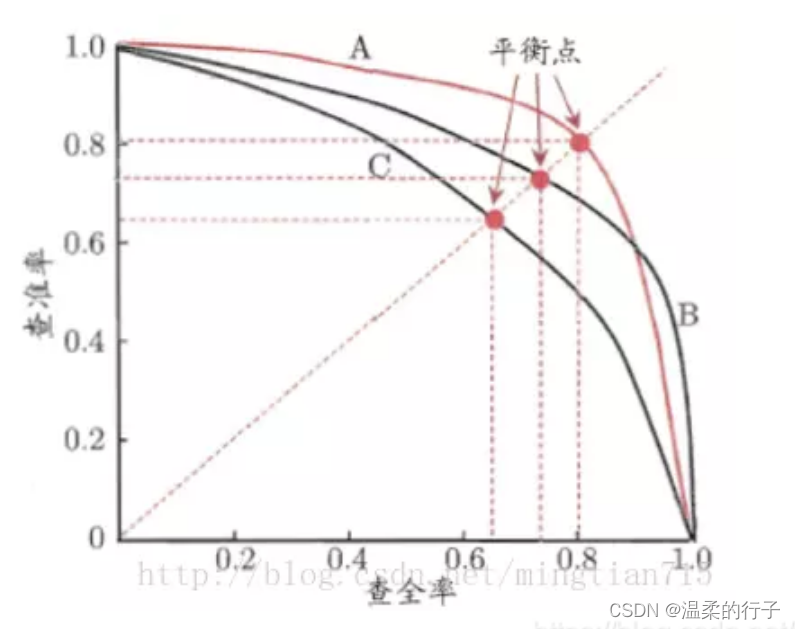
神经网络常见评价指标AUROC(AUC-ROC)、AUPR(AUC-PR)
神经网络的性能可以通过多个评价指标进行衡量,具体选择哪些指标取决于任务的性质。以下是神经网络中常见的评价指标: 准确性(Accuracy): 准确性是最常见的分类任务评价指标,表示模型正确预测的样本数占总样…...

Apache Doris安装部署
Apache Doris安装部署 版本: CentOS 7.6 Apache Doris 0.14.0 编译 选择合适的版本进行下载,此次选择0.14.0版本 下载 | Apache Doris 一、CentOS编译 1 安装依赖 sudo yum groupinstall Development Tools && sudo yum install maven c…...

Excel查询时用vlookup或者xlookup时,虽然用的参数选择的是精确匹配,但是发现不能区分大小写,应该如何解决?
Excel查询时用vlookup或者xlookup时,虽然用的参数选择的是精确匹配,但是发现不能区分大小写,应该如何解决? Index函数解决 INDEX([excel1.xlsx]Sheet1!$E:$E,MATCH(1,EXACT(G5,[excel1.xlsx]Sheet1!$E:$E)*1,0))重点说明&#x…...
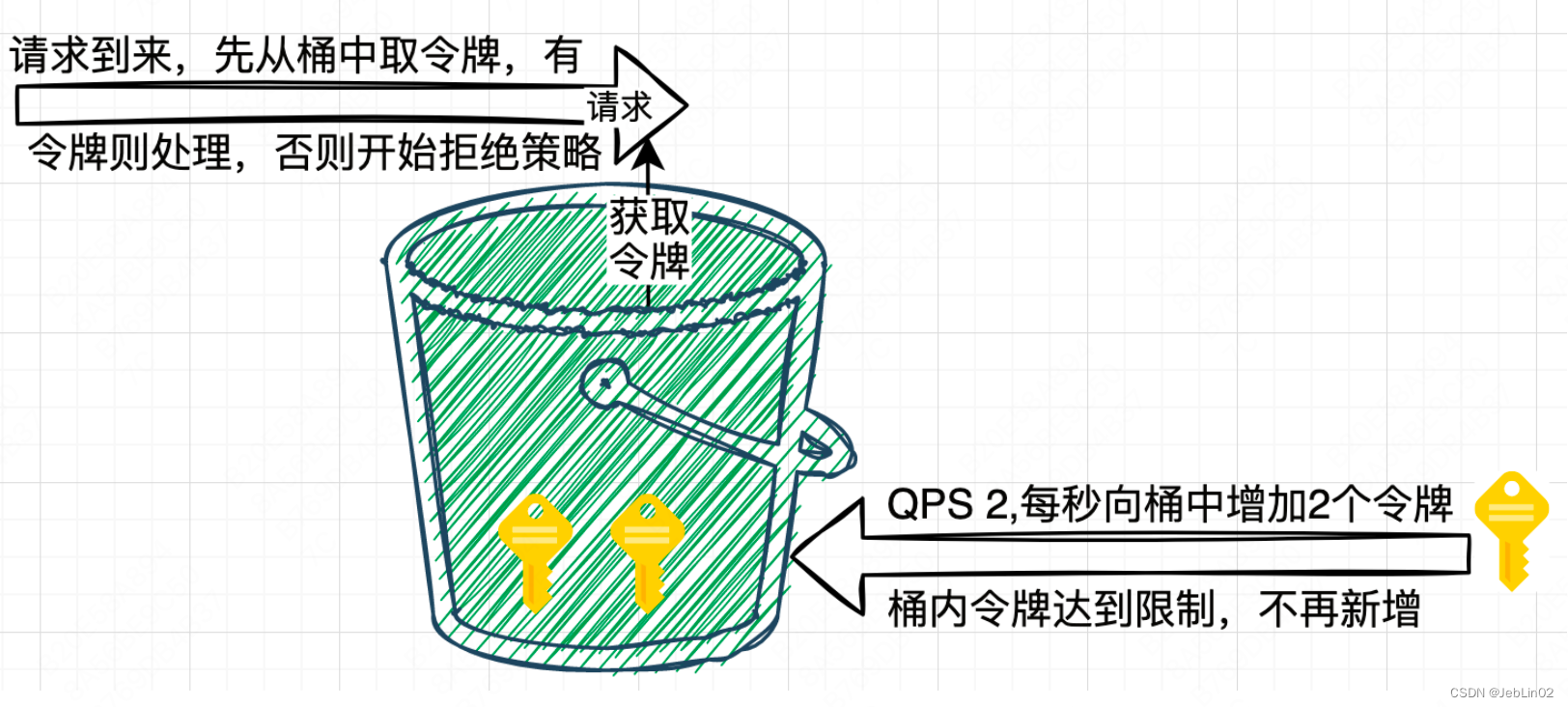
4种经典的限流算法
0、基础知识 1000毫秒内,允许2个请求,其他请求全部拒绝。 不拒绝就可能往db打请求,把db干爆~ interval 1000 rate 2; 一、固定窗口限流 固定窗口限流算法(Fixed Window Rate Limiting Algorithm)是…...
<MySQL> 什么是数据库事务?事务该如何使用?
目录 一、事务的概念 二、事务的核心特性 三、事务操作中的常见BUG 3.1 脏读 3.2 不可重复读 3.3 幻读 四、隔离级别 五、使用事务 一、事务的概念 “事务”是指一组操作,在逻辑上是不可分割的,组成这组操作的各个语句,或者全部执行成…...
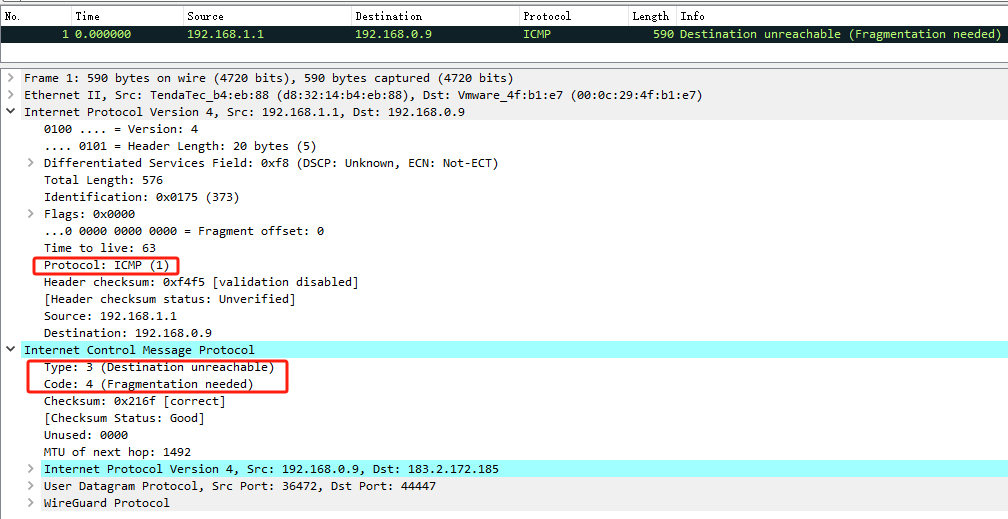
Linux 网络:PMTUD 简介
文章目录 1. 前言2. Path MTU Discovery(PMTUD) 协议2.1 PMTUD 发现最小 MTU 的过程 3. Linux 的 PMTUD 简析3.1 创建 socket 时初始化 PMTUD 模式3.2 数据发送时 PMTUD 相关处理3.2.1 源头主机发送过程中 PMTU 处理3.2.2 转发过程中 PMTUD 处理 4. PMTUD 观察5. 参考链接 1. 前…...

BatchNormalization:解决神经网络中的内部协变量偏移问题
ICML2015 截至目前51172引 论文链接 代码连接(planing) 文章提出的问题 减少神经网络隐藏层中的”内部协变量偏移”问题。 在机器学习领域存在“协变量偏移”问题,问题的前提是我们划分数据集的时候,训练集和测试集往往假设是独立同分布(i.i.d)的,这种独立同分布更有利于…...

DAC实验(DAC 输出三角波实验)(DAC 输出正弦波实验)
DAC 输出三角波实验 本实验我们来学习使用如何让 DAC 输出三角波,DAC 初始化部分还是用 DAC 输出实验 的,所以做本实验的前提是先学习 DAC 输出实验。 使用 DAC 输出三角波,通过 KEY0/KEY1 两个按键,控制 DAC1 的通道 1 输出两种…...
许多网友可能还不知道,升级到Windows 11其实没那么复杂,只要符合几个条件可以了
如果你的Windows 10电脑可以升级Windows 11,现在怎么办?有几种方法可以免费安装新的操作系统。以下是你的选择。 如果你想升级到Windows 11,你可以随时购买一台已经安装了操作系统的新电脑。然而,如果你目前的Windows 10 PC满足所有必要的升级要求,那么在Windows 11免费的…...
ubuntu下载conda
系统:Ubuntu18.04 (1)下载安装包 wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/Anaconda3-2021.11-Linux-x86_64.sh 报错错误 403:Forbidden 解决方法 wget -U NoSuchBrowser/1.0 https://mirrors.tuna.tsingh…...

重磅 | 进一步夯实生态建设,朗思科技与阿里龙蜥完成兼容性认证
近日,北京朗思智能科技有限公司(以下简称“朗思科技”)自主研发的数字员工产品与OpenAnolis龙蜥社区龙蜥操作系统(Anolis OS)8完成兼容性认证。测试结果显示,双方产品相互兼容,功能正常…...

Qt给控件添加图片
双击qrc文件,选择下面的addFiles,将图片添加进来,然后选中图片右键Select All 设置控件字符: ui.btnSet->setText(""); 设置资源: ui.btnSet->setStyleSheet("QPushButton{background-image:…...

3.6-Dockerfile语法梳理及最佳实践
WORKDIR是设置当前docker的工作目录 ADD 和 COPY 为了将本地的一些文件添加到docker image里面,ADD 和 COPY的作用特别像,但是ADD 和 COPY还有一些区别,ADD不仅可以添加本地文件到docker里面,还可以将文件在添加到docker image里面…...
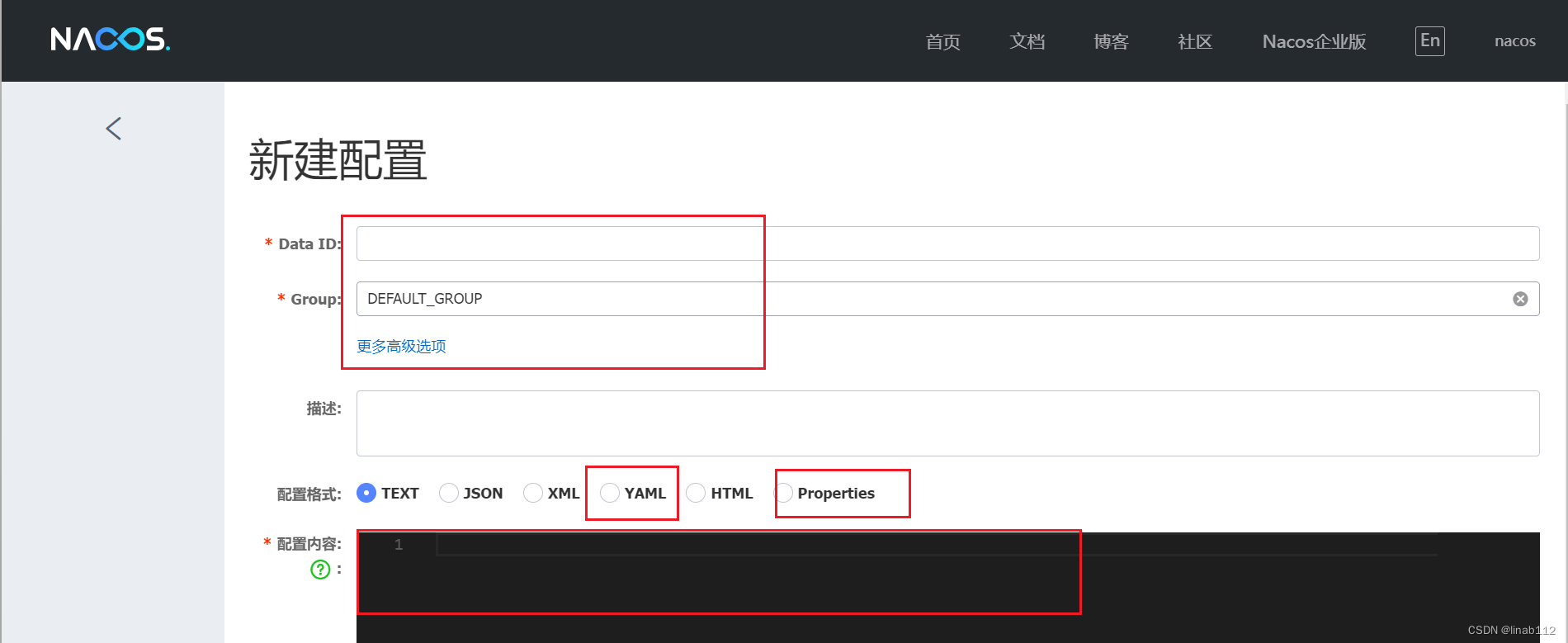
springboot集成nacos并实现自动刷新
目录 1.说明 2.示例 3.自动刷新的注意点 1.说明 springboot项目中存在好多配置文件,比如配置数据信息,redis信息等等,配置文件可以直接放在代码,也可以放在像nacos这样的组件中,实现动态的管理,修改配置…...

java面试八股文2023完整版详解110题附带答案
以下是一份Java面试八股文2023,涵盖了Java编程语言的核心概念和常用技术,帮助你更好地准备面试。 1. Java语言有哪些特点? Java语言是一种面向对象的编程语言,具有简单、面向对象、分布式、多线程、动态等优点。它是一种跨平台的…...

微服务实战系列之Token
前言 什么是“Token”? 它是服务端生成的一串字符串,以作客户端进行请求的一个令牌,当第一次登录后,服务器生成一个Token便返回给客户端;以后客户端只携带此Token请求数据即可。 简言之,Token其实就是用户身…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
