巴塞尔问题数值逼近方法
巴塞尔问题:计算所有平方数的导数和
∑n=1∞1n2=limn→+∞(112+122+⋯+1n2)\sum_{n=1}^{\infty} \frac{1}{n^{2}}=\lim _{n \rightarrow+\infty}\left(\frac{1}{1^{2}}+\frac{1}{2^{2}}+\cdots+\frac{1}{n^{2}}\right)n=1∑∞n21=n→+∞lim(121+221+⋯+n21)
其理论解为 1/6π21/6\pi^21/6π2
网络上有很多关于理论解的证明,此处不在赘述。下面介绍数值逼近的方法(也可以用此方法来求 π\piπ)
如果直接使用定义,通过matlab计算我们可以知道,前1e6次项,误差也有1e-6,误差还是比较大的。
n = 1e6;
num = 1:n;
a = sum(1./(num.^2))
err = zeta(2)-a
使用下面的加速算法,
ζ(2)∼∑k=1n1k2+1n−12n2+16n3−130n5+142n7−130n9\zeta(2) \sim \sum_{k=1}^{n} \frac{1}{k^{2}}+\frac{1}{n}-\frac{1}{2 n^{2}}+\frac{1}{6 n^{3}}-\frac{1}{30 n^{5}}+\frac{1}{42 n^{7}}-\frac{1}{30 n^{9}}ζ(2)∼k=1∑nk21+n1−2n21+6n31−30n51+42n71−30n91
n = 1e6;
num = 1:n;
a = sum(1./(num.^2))+1/n-1/(2*n^2)+1/(6*n^3)-1/(30*n^5)+1/(42*n^7)-1/(30*n^9);
err = zeta(2)-a
前1e6次项,误差达到了1e-16,结果让人满意。
上面的那个加速算法,是通过 Euler–Maclaurin 公式得到的。但是我自己也没有算明白,有兴趣的读者可以自己搜着看一下。
2023年2月28日19点36分
相关文章:

巴塞尔问题数值逼近方法
巴塞尔问题:计算所有平方数的导数和 ∑n1∞1n2limn→∞(112122⋯1n2)\sum_{n1}^{\infty} \frac{1}{n^{2}}\lim _{n \rightarrow\infty}\left(\frac{1}{1^{2}}\frac{1}{2^{2}}\cdots\frac{1}{n^{2}}\right)n1∑∞n21n→∞lim(121221⋯n21) 其理论解为…...

【深度学习环境】Docker
1. Docker 相关安装配置 1.1 docker 安装 参考:https://www.runoob.com/docker/ubuntu-docker-install.html 1.2 nvidia-docker 安装 参考:https://zhuanlan.zhihu.com/p/37519492 1.3 代理加速 参考:https://yeasy.gitbook.io/docker_…...
基于vscode开发vue项目的详细步骤教程 2 第三方图标库FontAwesome
1、Vue下载安装步骤的详细教程(亲测有效) 1_水w的博客-CSDN博客 2、Vue下载安装步骤的详细教程(亲测有效) 2 安装与创建默认项目_水w的博客-CSDN博客 3、基于vscode开发vue项目的详细步骤教程_水w的博客-CSDN博客 目录 六、第三方图标库FontAwesome 1 安装FontAwesome 解决报…...

今天面了个腾讯拿25K出来的软件测试工程师,让我见识到了真正的天花板...
今天上班开早会就是新人见面仪式,听说来了个很厉害的大佬,年纪还不大,是上家公司离职过来的,薪资已经达到中高等水平,很多人都好奇不已,能拿到这个薪资应该人不简单,果然,自我介绍的…...

OSG三维渲染引擎编程学习之六十九:“第六章:OSG场景工作机制” 之 “6.9 OSG数据变量”
目录 第六章 OSG场景工作机制 6.9 OSG数据变量 第六章 OSG场景工作机制 作为一个成熟的三维渲染引擎,需要提供快速获取场景数据、节点等信息,具备自定义数据或动画更新接口,能接收应用程序或窗口等各类消息。OSG三维渲染引擎能较好地完成上述工作,OSG是采用什么方式或工作…...

Tektronix泰克TDP3500差分探头3.5GHz
附加功能: 带宽:3.5 GHz 差分输入电容:≤0.3 pF 差分输入电阻:100 kΩ DC pk 交流输入电压:15 V >60 dB 在 1 MHz 和 >25 dB 在 1 GHz CMRR 出色的共模抑制——减少较高共模环境中的测量误差 低电容和电阻负载…...
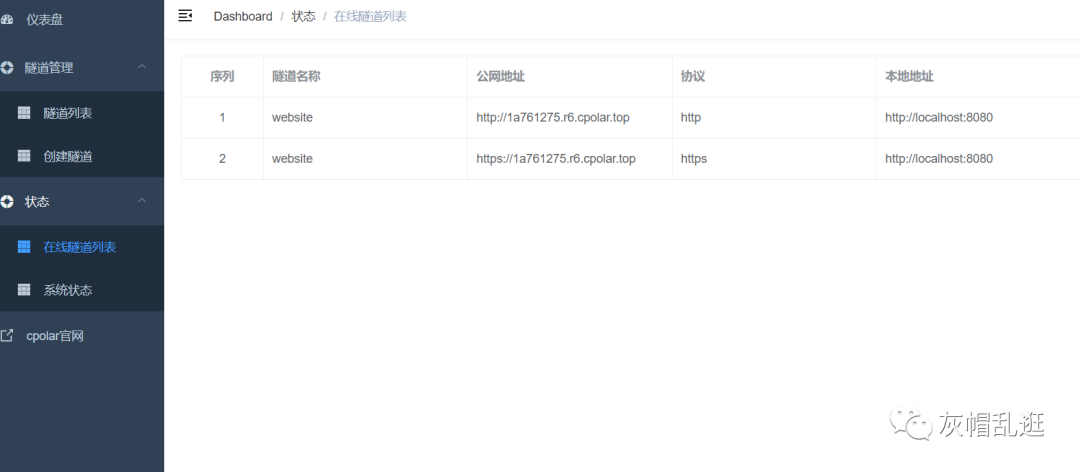
轻松实现内网穿透:实现远程访问你的私人网络
导语:内网穿透是什么?为什么我们需要它?今天我们将介绍这个令人惊叹的技术,让你实现远程访问你的私人网络。 使用内网穿透,轻松实现外网访问本地部署的网站 第一部分:什么是内网穿透? 通俗解释…...

MySQL长字符截断
MySQL超长字符截断又名"SQL-Column-Truncation",是安全研究者Stefan Esser在2008 年8月提出的。 在MySQL中的一个设置里有一个sql_mode选项,当sql_mode设置为default时,即没有开启STRICT_ALL_TABLES选项时(MySQLsql_mo…...

python计算量比指标
百度百科是这么写的:量比定义:股市开市后平均每分钟的成交量与过去5个交易日平均每分钟成交量之比。计算公式:量比(现成交总手数 / 现累计开市时间(分) )/ 过去5日平均每分钟成交量。这里公式没有问题,但是…...
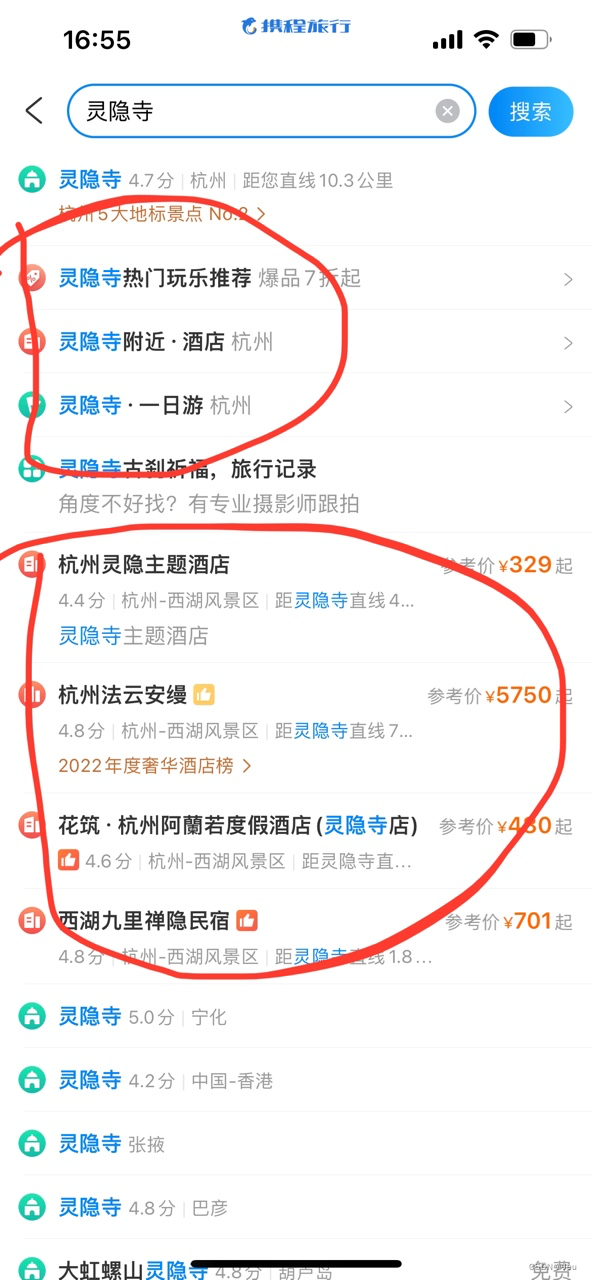
下拉框推荐-Suggest-SUG
什么是下拉框推荐 在我们使用各种app(飞猪)想要搜索我们想要的东西,假设我想要上海迪士尼的门票,那么精确的query是“上海迪士尼门票”,要打7个字,如果在你输入“上海”的时候app就推荐了query“上海迪士尼…...

Nmap的几种扫描方式以及相应的命令
Nmap是一款常用的网络扫描工具,它可以扫描目标网络上的主机和服务,帮助安全研究员了解目标网络的拓扑结构和安全情况。以下是Nmap的几种扫描方式以及相应的命令: 1.Ping扫描 Ping扫描可以用来探测网络上响应的主机,可以使用“-sn…...
Qt::QOpenGLWidget 渲染天空壳
在qt窗口中嵌入opengl渲染天空壳和各种立方体一 学前知识天空壳的渲染学前小知识1 立方体贴图 天空壳的渲染就是利用立方体贴图来实现渲染流程2 基础光照 光照模型3 opengl帧缓冲 如何自定义帧缓冲实现后期特效4 glsl常见的shader内置函数 glsl编程常用的内置函数二 shader代码…...
谷歌搜索技巧大全 | 谷歌高级搜索语法指令
谷歌搜索技巧是利用各种高级搜索语法或者搜索指令,让我们能够使用Google进行精确化的搜索,外贸找客户和学术文件查找都可以应用到这些搜索技巧。(大部分命令也适用百度搜索)。Google通过互联网收集数据,抓取有意义的信息,将其存储…...

JAVA开发(JAVA垃圾回收的几种常见算法)
JAVA GC 是JAVA虚拟机中的一个系统或者说是一个服务,专门是用于内存回收,交还给虚拟机的功能。 JAVA语言相对其他语言除了跨平台性,还有一个最重要的功能是JAVA语言封装了对内存的自动回收。俗称垃圾回收器。所以有时候我们不得不承认&#…...
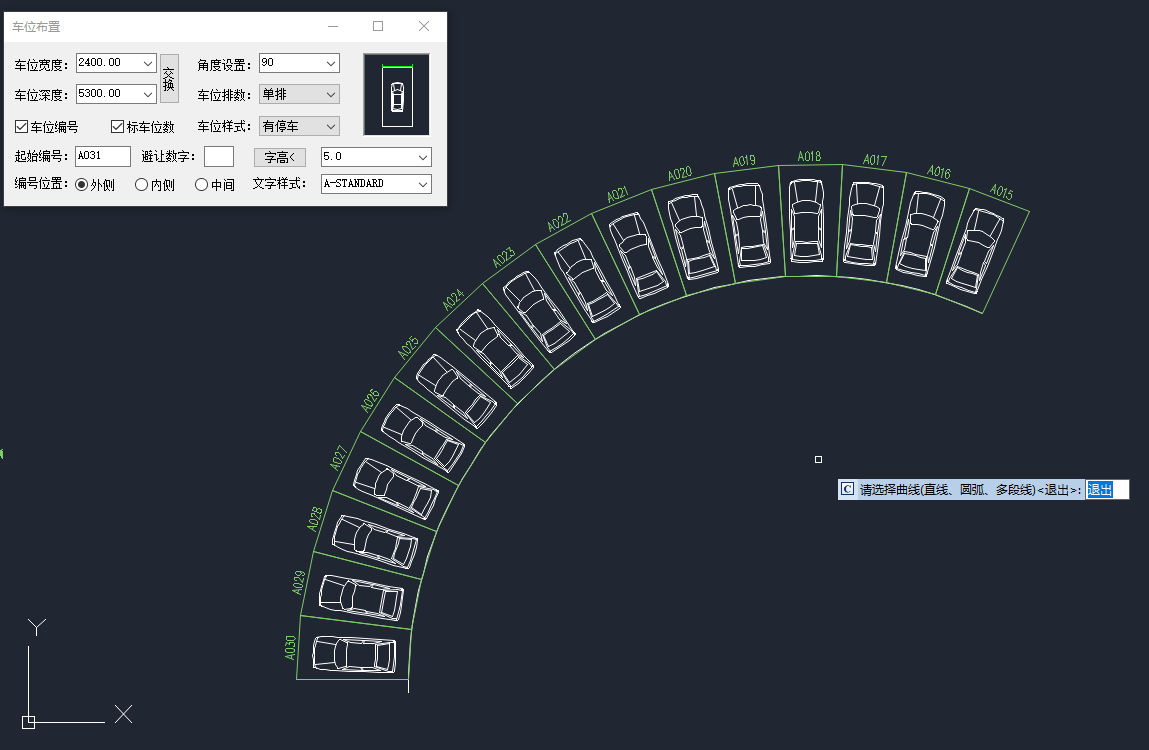
你还不会用CAD一键布置停车位?赶紧学起来!
在设计CAD建筑图的过程中,你还在一个一个地画停车位吗?那未免也太低效了吧!今天,小编用浩辰CAD建筑软件来教大家一键布置停车位,赶紧学起来吧! 浩辰CAD建筑软件是行业应用最广泛的创新型建筑设计专业软件&…...

【MySQL之MySQL底层分析篇】系统学习MySQL,从应用SQL语法到底层知识讲解,这将是你见过最完成的知识体系
文章目录MySQL体系结构MySQL存储结构(以InnoDB为例)MySQL执行流程(以InnoDB为例)1. 数据写入原理2. 数据查询原理MySQL存储引擎1. 为什么需要不同的存储引擎2. 如何为数据指定不同的存储引擎,数据粒度又是多少3. MySQL…...
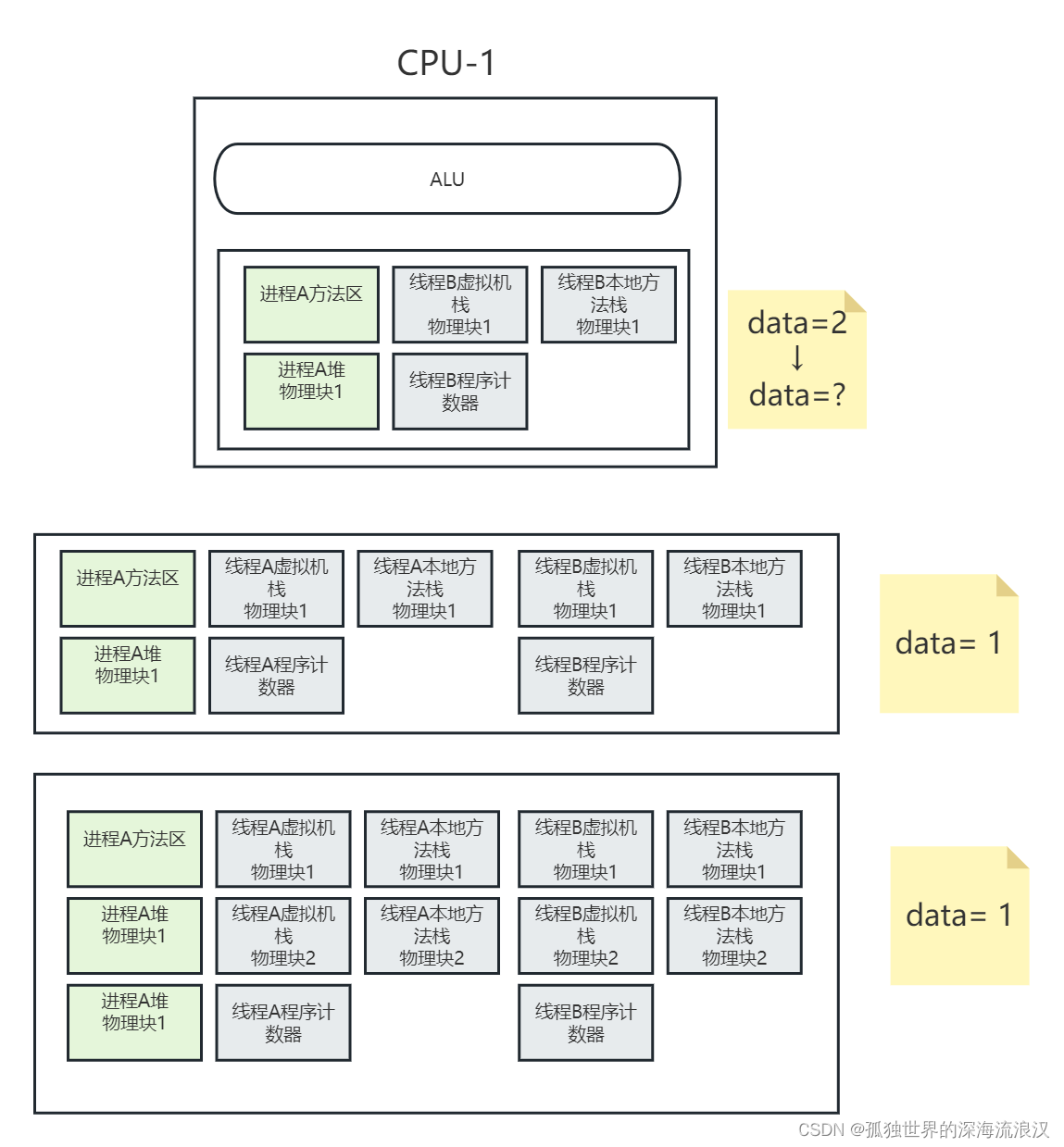
单核CPU是否有线程可见性问题?
本文仅是本人对问题的思考记录,并没有实操验证,有误请大家评论指出。 今天见到了一个经典的问题,单核CPU是否有线程可见性问题,学完操作系统应该可以直接回答,不会有线程安全问题。但如果结合JVM虚拟机来进行分析&…...
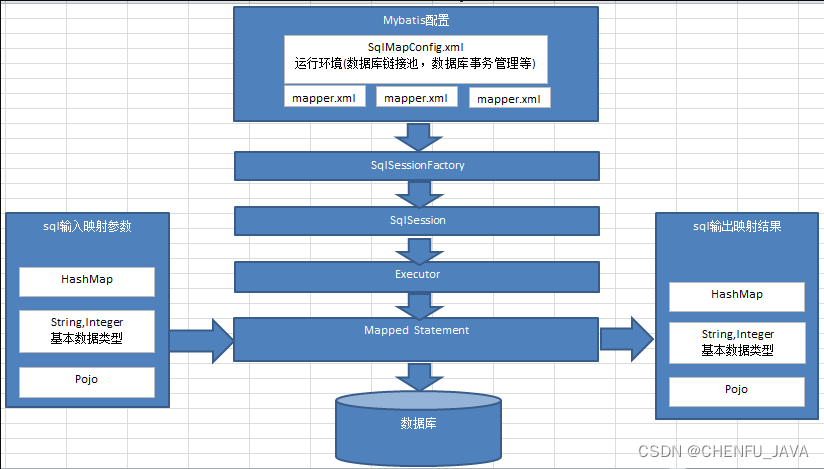
MyBatis 架构介绍
MyBatis 架构介绍MyBatis 架构图MyBatis 所解决的 JDBC 中存在的问题引用MyBatis 架构图 mybatis 配置:mybatis-config.xml,此文件作为 mybatis 的全局配置文件,配置了 mybatis 的运行环境等信息。另一个 mapper.xml 文件即 sql 映射文件,文件…...

加密算法---RSA 非对称加密原理及使用
加密算法---RSA 非对称加密原理及使用一 非对称加密原理介绍二 加密解密测试2.1 加密解密工具类2.2 测试一 非对称加密原理介绍 非对称加密算法中,有两个密钥:公钥和私钥。它们是一对,如果用公钥进行加密,只有用对应的私钥才能解…...

MySQL-查询语句
数据库管理系统的一个最重要的功能就是数据查询,数据查询不应只是简单查询数据库中存储的数据,还应该根据需要对数据进行筛选,以及确定数据以什么样的格式显示。MySQL提供了功能强大、灵活的语句来实现这些操作。下面是通过help帮助查看到的s…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
