【华为OD题库-026】通过软盘拷贝文件-java
题目
有一名科学家想要从一台古董电脑中拷贝文件到自己的电脑中加以研究。但此电脑除了有一个3.5寸软盘驱动器以外,没有任何手段可以将文件拷贝出来,而且只有一张软盘可以使用。因此这一张软盘是唯一可以用来拷贝文件的载体。科学家想要尽可能多地将计算机中的信息拷贝到软盘中,做到软盘中文件内容总大小最大。已知该软盘容量为1474560字节。文件占用的软盘空间都是按块分配的,每个块大小为512个字节。一个块只能被一个文件使用。拷贝到软盘中的文件必须是完整的,且不能采取任何压缩技术。
输入描述
第1行为一个整数N,表示计算机中的文件数量。1<= N<= 1000
接下来的第2行到第N+1行(共N行),每行为一个整数,表示每个文件的大小Si,单位为字节.0<=i<N;i<=Si
输出描述
科学家最多能拷贝的文件总大小
备注
为了充分利用软盘空间,将每个文件在软盘上占用的块记录到本子上。即真正占用软盘空间的只有文件内容本身
示例1:
输入
3
737270
737272
737288
输出
1474542
说明
3个文件中,每个文件实际占用的大小分别为737280字节737280字节、737792字节。
只能选取前两个文件,总大小为1474542字节。虽然后两个文件总大小更大且未超过1474560字节,但因为实际占用的大小超过了1474560字节,所以不能选后两个文件。
示例2:
输入
6
400000
200000
200000
200000
400000
400000
输出
1400000
说明
从6个文件中,选择3个大小为400000的文件和1个大小为200000的文件,得到最大总大小为1400000;
也可以选择2个大小为400000的文件和3个大小为200000的文件,得到的总大小也是1400000.
思路
题目翻译过来就是:在N个数字中选若干数字(子集),使其占用的总的块大小(大小/512.0)不超过1474560/512=2880。求所有子集中容量的最大值?需要注意的是:
一个块只能被一个文件使用,假设一个文件大小为737270,转为块大小:737270/512.0=1439.98046875,此处不管小数部分是多少,都只能向上取整(超出一点点,也只能存到一个新的块中)。即占用1440个块大小,实际占用空间为1440 * 512=737280。
可以有两种思路来解决:
- 按照组合的思想,找出所有满足条件的组合,然后求容量最大值
- 典型的背包问题,可用动态规划解决
组合思想之前写过博客专门介绍,本文不赘述,直接给出题解。传送门:【JAVA-排列组合】一个套路速解排列组合题
本节重点介绍动态规划思想。
定义二维数组:
dp[i][j]:代表从数组nums的前(i+1)个文件(即nums[0:i])中选则任意个文件,使其占用的block不超过j,能够得到的文件的最大大小总和。
- 确定i的取值范围:i刚好对应nums的下标。范围为[0,nums.length-1]
- 确定j的取值范围:根据题目描述,最大block为:1474560/512=2880个,范围为[0,2880]
- 因此,dp初始化时,可以写为new int[nums.length][2881]
初始化dp
1.dp[i][0]代表,最多选nums前(i+1)个文件,使其占用的block个数不超过0时的最大文件和,很明显只要选了文件,其占用的block就不可能为0个,所以dp[i][0]=0
2.dp[0][j]代表,最多选取第一个文件,即nums[0],使其占用空间不超过j个block时的最大文件和。首先需要计算选则的文件占用的block大小:curBlock=Math.ceil(nums[0] / 512.0),如果j的大小比curBlock还小,说明不能放入nums[0]这个文件,反之,如果j>=curBlock,那么此时的dp[0][j]=nums[0]。确定递推关系
对于dp[i][j](i>=1,j>=1)来说。对于当前文件nums[i]只有选取或者不选取两种状态:记录当前nums[i]文件占用的block大小为:curBlock=Math.ceil(nums[i] / 512.0)。
不选取:不选取就是从前i-1个元素中去选取不超过j个block大小的结果,那么dp[i][j]=dp[i-1][j]
选取:此时的结果应该等于未选当前值的结果+当前值的大小。即:dp[i-1][j-curBlock]+nums[i]
最后dp[i][j]取两种状态的最大值即可,即dp[i][j]=max(dp[i-1][j],dp[i-1][j-curBlock]+nums[i])有了初始值和递推关系,可以得到我们需要的结果:dp[nums.length-1][2880]
题解
方案一:组合思想
package hwod;import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;public class CopyFileFromSoftDisk {private static int max_block = (int) Math.ceil(1474560 / 512.0);private static int ans = -1;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[] nums = new int[n];for (int i = 0; i < n; i++) {nums[i] = sc.nextInt();}System.out.println(copyFileFromSoftDisk(nums));}private static int copyFileFromSoftDisk(int[] nums) {LinkedList<Integer> path = new LinkedList<>();Arrays.sort(nums);int[] used = new int[nums.length];dfs(nums, 0, path, used, 0, 0);return ans;}private static void dfs(int[] nums, int begin, LinkedList<Integer> path, int[] used, int sum, int block) {if (block > max_block) return;ans = Math.max(sum, ans);for (int i = begin; i < nums.length; i++) {if (i > begin && nums[i] == nums[i - 1] && used[i - 1] == 0) break;//同层重复剪枝path.addLast(nums[i]);used[i] = 1;dfs(nums, i + 1, path, used, sum + nums[i], block + (int) Math.ceil(nums[i] / 512.0));path.removeLast();used[i] = 0;}}
}方案二:动态规划
package hwod;import java.util.Scanner;public class CopyFileFromSoftDisk2 {private static int max_block = (int) Math.ceil(1474560 / 512.0);private static int ans = -1;private static int cnt = 0;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[] nums = new int[n];for (int i = 0; i < n; i++) {nums[i] = sc.nextInt();}System.out.println(copyFileFromSoftDisk(nums));}private static int copyFileFromSoftDisk(int[] nums) {int m = nums.length, n = max_block;int[][] dp = new int[m][n + 1];for (int i = (int) Math.ceil(nums[0] / 512.0); i < n + 1; i++) {dp[0][i] = nums[i];}for (int i = 1; i < m; i++) {for (int j = 1; j < n + 1; j++) {int curBlock = (int) Math.ceil(nums[i] / 512.0);dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - curBlock] + nums[i]);}}return dp[m - 1][n];}
}推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。
相关文章:

【华为OD题库-026】通过软盘拷贝文件-java
题目 有一名科学家想要从一台古董电脑中拷贝文件到自己的电脑中加以研究。但此电脑除了有一个3.5寸软盘驱动器以外,没有任何手段可以将文件拷贝出来,而且只有一张软盘可以使用。因此这一张软盘是唯一可以用来拷贝文件的载体。科学家想要尽可能多地将计算…...

定量数据和定性数据
定量数据本质上是数值,应该是衡量某样东西的数量。 定性数据本质上是类别,应该是描述某样东西的性质。 全部的数据列如下,其中既有定性列也有定量列; import pandas as pdpd.options.display.max_columns None pd.set_option(e…...
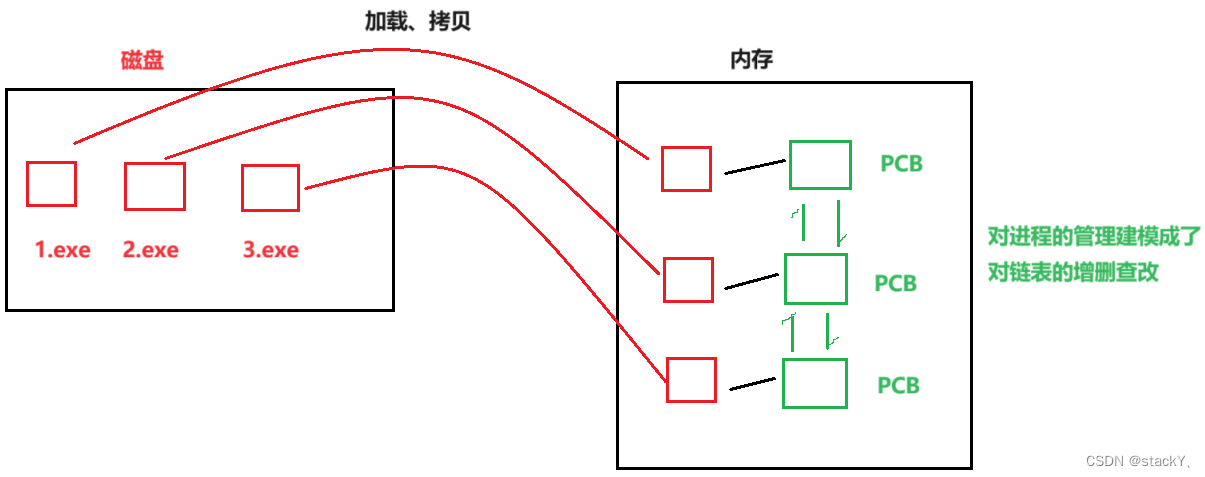
【Linux】:体系结构与进程概念
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux体系结构和进程的知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入…...

react-router-dom 版本6.18.0中NavLink的api和属性介绍
React Router 是一个基于 React 的路由库,它可以帮助我们在 React 应用中实现页面的切换和路由的管理。而 NavLink 则是 React Router 中的一个组件,它可以帮助我们实现导航栏的样式设置和路由跳转。 在 React Router 版本6.18.0 中,NavLink…...
和KD树区别?2d tree与3d tree区别?)
八叉树(Octree)和KD树区别?2d tree与3d tree区别?
一、八叉树(Octree)和KD树 八叉树(Octree) 结构:八叉树是一种用于三维空间数据的树状结构,每个分支节点恰好有八个子节点。每个节点代表空间中的一个立方体区域,这个立方体区域被均匀地分割成…...
)
Union(联合体、共用体)
结构体和共用体的区别在于:结构体的各个成员会占用不同的内存,互相之间没有影响;而共用体的所有成员占用同一段内存,修改一个成员会影响其余所有成员。 结构体占用的内存大于等于所有成员占用的内存的总和(成员之间可能…...

C++11的互斥包装器
文章目录 1. 为何要引入互斥包装器?2. lock_guard3. unique_lock4. 两者之间的不同5. 总结 1. 为何要引入互斥包装器? 在C多线程中会经常用到mutex,在使用的时候lock后,有时候会忘记使用unlock进行解锁造成死锁,或者在…...
HR应用在线人才测评,给企业招聘带来的好处
一、什么是人才测评? 人才测评是指运用一系列的科学方法,对人的基本素质,专业能力,心理健康,性格进行选拔,评价及发展人才的一种科学方法。近十多年,它被广泛运用于国有大型企业的人才招聘和人…...

深入了解百度爬虫工作原理
在当今数字化时代,互联网已经成为人们获取信息的主要渠道之一。而搜索引擎作为互联网上最重要的工具之一,扮演着连接用户与海量信息的桥梁角色。然而,我们是否曾经好奇过当我们在搜索引擎中输入关键词并点击搜索按钮后,究竟是如何…...

【C语言基础】分享近期学习到的volatile关键字、__NOP__()函数以及# #if 1 #endif
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

docker容器自启动
场景 当服务器关机重启后,docker容器每次都要去docker start 容器id 怎么可以下次让它自启动呢? 解决 先 # docker ps -a 查到之前启动过的容器id # docker update --restartalways 容器id重启后,reboot,就不用再单独去启动容…...

【C++】:模板的使用
目录 1、泛型编程 2、函数模板 2.1、函数模板概念 2.2、函数模板格式 2.3、函数模板的原理 2.4、函数模板的实例化 2.6、模板参数的匹配原则 3、类模板 3.1、 类模板的定义格式 3.2、 类模板的实例化 4、非类型模板参数 5、模板的特化 5.1、函数模板特化 5.2、类模…...

Springboot框架中使用 Redis + Lua 脚本进行限流功能
Springboot框架中使用 Redis Lua 脚本进行限流功能 限流是一种用于控制系统资源利用率或确保服务质量的策略。在Web应用中,限流通常用于控制接口请求的频率,防止过多的请求导致系统负载过大或者防止恶意攻击。 什么是限流? 限流是一种通过…...
 人名分类器实战项目(对比RNN、LSTM、GRU模型))
【nlp】2.5(cpu version) 人名分类器实战项目(对比RNN、LSTM、GRU模型)
人名分类器实战项目 0 项目说明1 案例介绍2 案例步骤2.1 导入必备的工具包2.2 数据预处理2.2.1 获取常用的字符数量2.2.2 国家名种类数和个数2.2.3 读数据到python环境中2.2.4 构建数据源NameClassDataset2.2.5 构建迭代器遍历数据2.3 构建RNN及其变体模型2.3.1 构建RNN模型2.3…...
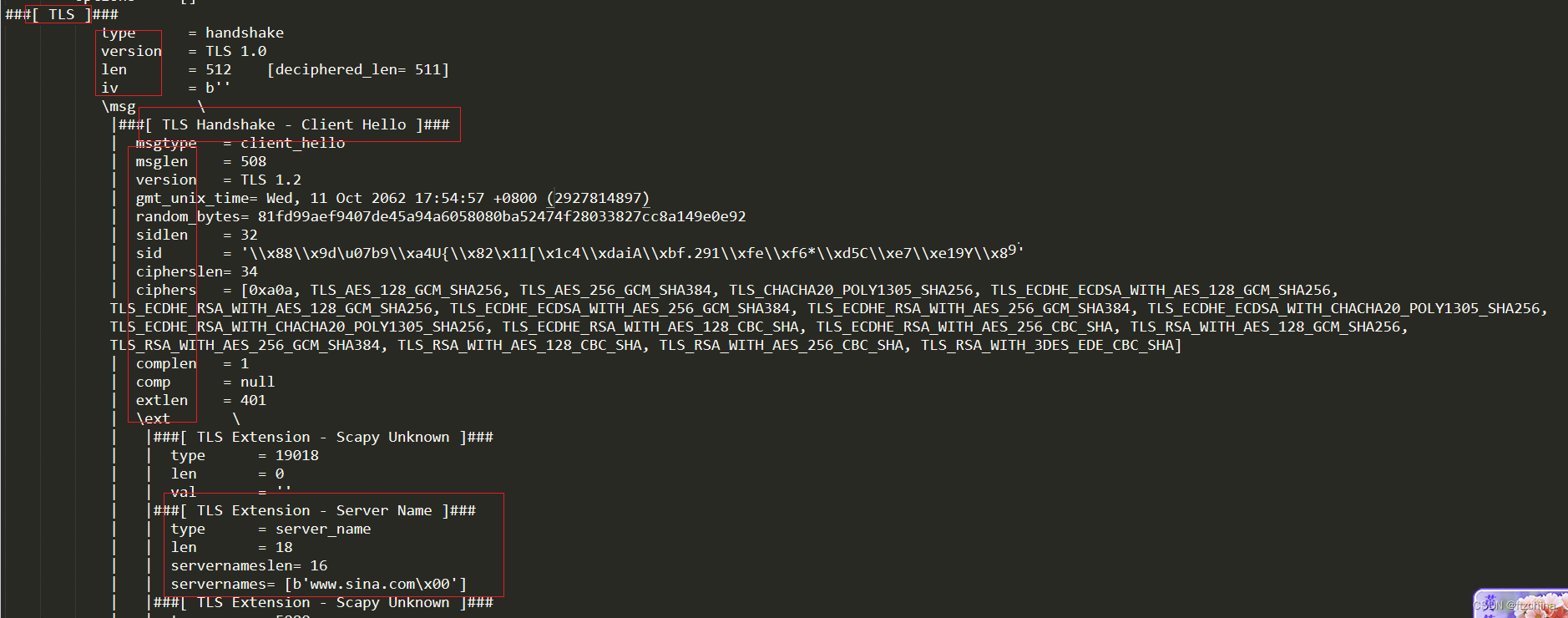
记录基于scapy构造ClientHello报文的尝试
最近有个需求就是用scapy构造https的client hello报文,由用户指定servername构造对应的报文。网上对于此的资料甚少,有的也是怎么去解析https报文,但是对于如果构造基本上没有找到相关的资料。 一直觉得最好的老师就是Python的help功能和dir功…...

程序设计实践学习笔记
第1题 题目描述 创建一个返回四舍五入到最接近整数的分数之和的函数。在矩阵中有每行的第一个数字表示分子,第二个数子表示分母,挑战者需要将该分数的结果进行四舍五入并将矩阵中所有分数结果总和进行返回。 输入输出格式 输入格式 数字 N 表示的是矩阵的行数。…...
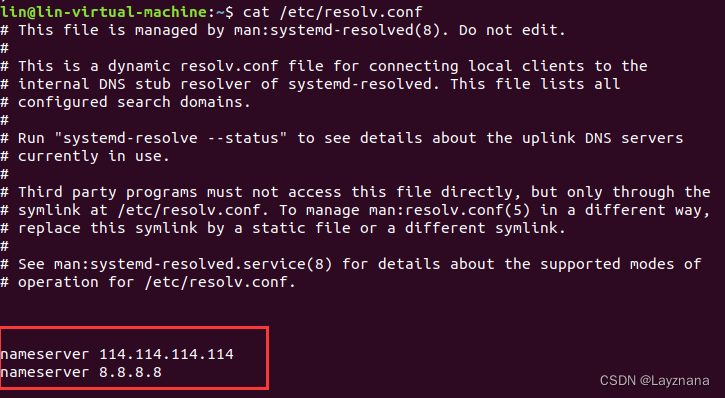
Ubuntu中apt-get update显示域名解析失败
第一步 检查主机->虚拟机能否ping成功 ping 红色框中的IPv4地址 能通,表示虚拟机ip配置成功;否则,需要先配置虚拟机ip 第二步 检查是否能ping成功百度网址 ping www.baidu.com 若不成功,可能原因 虚拟机没联网,打开火狐浏览器…...

go学习之简单项目
项目 文章目录 项目1.项目开发流程图2.家庭收支记账软件项目2)项目代码实现3)具体功能实现 3.客户信息管理系统1)项目需求说明2)界面设计3)项目框架图4)流程5)完成显示客户列表的功能6ÿ…...

代码随想录二刷 | 数组 | 总结篇
代码随想录二刷 | 数组 | 总结篇 基础知识二分查找移除元素有序数组的平方长度最小的数组最小覆盖子串螺旋数组 基础知识 定义:数组是存放在连续内存空间上的相同类型数据的集合 特点: 数组下标从 0 开始数组内存空间的地址是连…...

go test 命令详解
文章目录 1.简介2.test flag3.test/binary flags4.常用选项5.示例参考文献 1.简介 go test 是 Go 用来执行测试函数(test function)、基准函数(benchmark function)和示例函数(example function)的命令。 …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
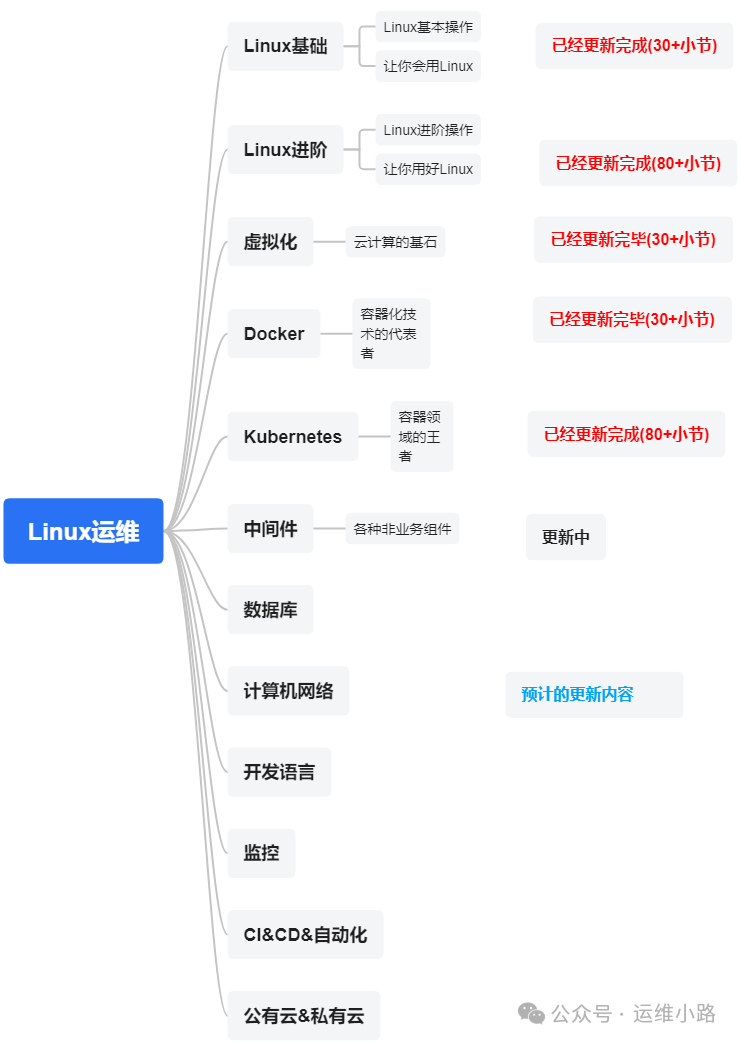
代理服务器-LVS的3种模式与调度算法
作者介绍:简历上没有一个精通的运维工程师。请点击上方的蓝色《运维小路》关注我,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 我们上一章介绍了Web服务器,其中以Nginx为主,本章我们来讲解几个代理软件:…...

uni-app学习笔记二十三--交互反馈showToast用法
showToast部分文档位于uniapp官网-->API-->界面:uni.showToast(OBJECT) | uni-app官网 uni.showToast(OBJECT) 用于显示消息提示框 OBJECT参数说明 参数类型必填说明平台差异说明titleString是提示的内容,长度与 icon 取值有关。iconString否图…...

【Elasticsearch基础】Elasticsearch批量操作(Bulk API)深度解析与实践指南
目录 1 Bulk API概述 1.1 什么是批量操作 1.2 Bulk API的优势 2 Bulk API的工作原理 2.1 请求处理流程 2.2 底层机制 3 Bulk API的使用方法 3.1 基本请求格式 3.2 操作类型示例 3.3 响应格式 4 Bulk API的最佳实践 4.1 批量大小优化 4.2 错误处理策略 4.3 性能调…...
