【数据结构&C++】二叉平衡搜索树-AVL树(25)
前言
大家好吖,欢迎来到 YY 滴C++系列 ,热烈欢迎! 本章主要内容面向接触过C++的老铁
主要内容含:
欢迎订阅 YY滴C++专栏!更多干货持续更新!以下是传送门!
目录
- 一.AVL树的概念
- 二.AVL树节点的定义(代码演示)
- 三.Avl树的基本操作:插入
- 四.AVL树的核心操作:旋转
- 【1】新节点插入较高右子树的右侧---右右:左单旋
- 【2】新节点插入较高左子树的左侧—左左:右单旋
- 【3】新节点插入较高左子树的右侧---左右:先左单旋再右单旋
- 【4】新节点插入较高右子树的左侧---右左:先右单旋再左单旋
- 五.AVL树的验证
- 1. 验证其为二叉搜索树
- 2. 验证其为平衡树
- 六.AVL树的性能&引入红黑树
- 七.AVL树的完整代码
一.AVL树的概念
- 二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证 每个结点的左右子树高度之差的绝对值不超过1 (需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
- 平衡因子是-1,左比右高1;平衡因子是1,右比左高1;平衡因子是0,左右一样高
- 一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
1. 它的左右子树都是AVL树
2. 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)- 如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在
O ( l o g 2 n ) O(log_2 n) O(log2n),搜索时间复杂度O( l o g 2 n log_2 n log2n)。
二.AVL树节点的定义(代码演示)
- 除了基本的左右孩子节点与数据外,还需要引入平衡因子
- 由于平衡因子取决于左右子树相对高度,所以节点本身 要能够返回父亲节点 ——> 要设置指向父亲节点的指针
- 注意AVL树节点是三叉链
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft; // 该节点的左孩子AVLTreeNode<T>* _pRight; // 该节点的右孩子AVLTreeNode<T>* _pParent; // 该节点的父亲节点T _data;int _bf; // 该节点的平衡因子
};
三.Avl树的基本操作:插入
- AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么 AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子
- AVL树的插入过程:
- 与二叉搜索树同理,二叉搜索树博客传送门:https://blog.csdn.net/YYDsis/article/details/134374001?spm=1001.2014.3001.5501
- 平衡因子的变化步骤:
- 新增在左,parent平衡因子减减
- 新增在右,parent平衡因子加加
- 平衡因子==0,高度不变,直接break
- 平衡因子==1/-1,高度改变-> 会影响祖先 -> 需要继续沿着到根节点root的路径向上更新
- 平衡因子==2/-2,高度改变& 树不再平衡 ->会影响祖先->需要对parent所在子树进行 旋转 操作,让其平衡 (旋转部分放在part4中详解)
- 向上更新,直到根节点(根节点parent==0)
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}//1. 按照二叉搜索树的方式插入新节点Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//2. 调整节点的平衡因子while (parent)//向上更新,直到根节点(根节点parent==0){if (cur == parent->_left)// 1.新增在左,parent平衡因子减减{parent->_bf--;}else // if (cur == parent->_right){parent->_bf++;//2.新增在右,parent平衡因子加加}if (parent->_bf == 0)//3.平衡因子==0,高度不变,直接break{// 更新结束break;}//4.平衡因子==1/-1,高度改变-> 会影响祖先 -> 需要继续沿着到根节点root的路径向上更新else if (parent->_bf == 1 || parent->_bf == -1){// 继续往上更新cur = parent;parent = parent->_parent;}//平衡因子==2/-2,高度改变& 树不再平衡 ->会影响祖先->//需要对parent所在子树进行 旋转 操作,让其平衡else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要旋转 (旋转部分为何这么设计放在part4中详解)if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{assert(false);}}return true;}
四.AVL树的核心操作:旋转
- 根据part3中avl树的基本操作"插入",以下情况会出现旋转
- 平衡因子==2/-2,高度改变& 树不再平衡 ->会影响祖先->需要对parent所在子树进行 旋转 操作,让其平衡 (旋转部分放在part4中详解)
- 所以一共有四种情况分别如下图所示:
- 旋转要注意以下两点:
1. 保持这颗树还是搜索树
2. 变成平衡树&降低其高度
【1】新节点插入较高右子树的右侧—右右:左单旋
- 分析:
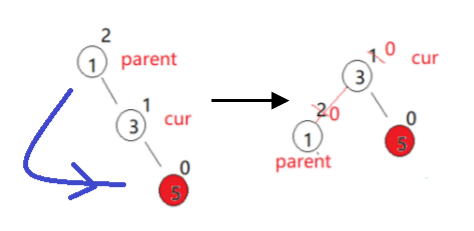
- 如下图所示,新节点插入较高右子树的右侧时候,整体会发生“向左的单旋”
- 核心操作:
cur->_right = parent;
parent->_parent = cur;
- 代码展示:
void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}
【2】新节点插入较高左子树的左侧—左左:右单旋
【3】新节点插入较高左子树的右侧—左右:先左单旋再右单旋
【4】新节点插入较高右子树的左侧—右左:先右单旋再左单旋
五.AVL树的验证
1. 验证其为二叉搜索树
- 如果其通过 中序遍历 可得到一个有序的序列,就说明为二叉搜索树
2. 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
六.AVL树的性能&引入红黑树
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这
样可以保证查询时高效的时间复杂度,即 l o g 2 ( N ) log_2 (N) log2(N)。但是如果要对AVL树做一些结构修改的操
作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,
有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数
据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。 因此需要
引入红黑树,传送门如下所示:红黑树博客传送门:
七.AVL树的完整代码
#pragma once#include<iostream>
#include<assert.h>
using namespace std;template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// ... 控制平衡// 更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else // if (cur == parent->_right){parent->_bf++;}if (parent->_bf == 0){// 更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{assert(false);}}return true;}void RotateL(Node* parent){++_rotateCount;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateR(Node* parent){++_rotateCount;Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}}int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;int leftHight = Height(root->_left);int rightHight = Height(root->_right);if (rightHight - leftHight != root->_bf){cout << "平衡因子异常:" <<root->_kv.first<<"->"<< root->_bf << endl;return false;}return abs(rightHight - leftHight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}private:Node* _root = nullptr;public:int _rotateCount = 0;
};
相关文章:
【数据结构&C++】二叉平衡搜索树-AVL树(25)
前言 大家好吖,欢迎来到 YY 滴C系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! 目录 一.AVL树的概念二.AVL树节点的定义(代码…...

Python算法——树的最大深度和最小深度
Python中的树的最大深度和最小深度算法详解 树的最大深度和最小深度是树结构中的两个关键指标,它们分别表示树的从根节点到最深叶子节点的最大路径长度和最小路径长度。在本文中,我们将深入讨论如何计算树的最大深度和最小深度,并提供Python…...

46.全排列-py
46.全排列 class Solution(object):def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""# 结果数组0ans[]nlen(nums)# 判断是否使用state_[False]*n# 临时状态数组dp_[]def dfs (index):# 终止条件if indexn:ans.appe…...
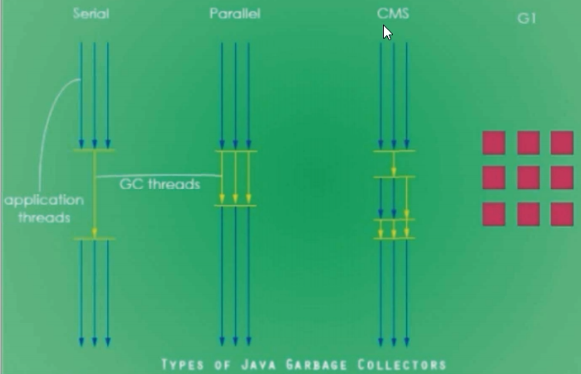
系列三、GC垃圾回收算法和垃圾收集器的关系?分别是什么请你谈谈
一、关系 GC算法(引用计数法、复制算法、标记清除算法、标记整理算法)是方法论,垃圾收集器是算法的落地实现。 二、4种主要垃圾收集器 4.1、串行垃圾收集器(Serial) 它为单线程环境设计,并且只使用一个线程…...
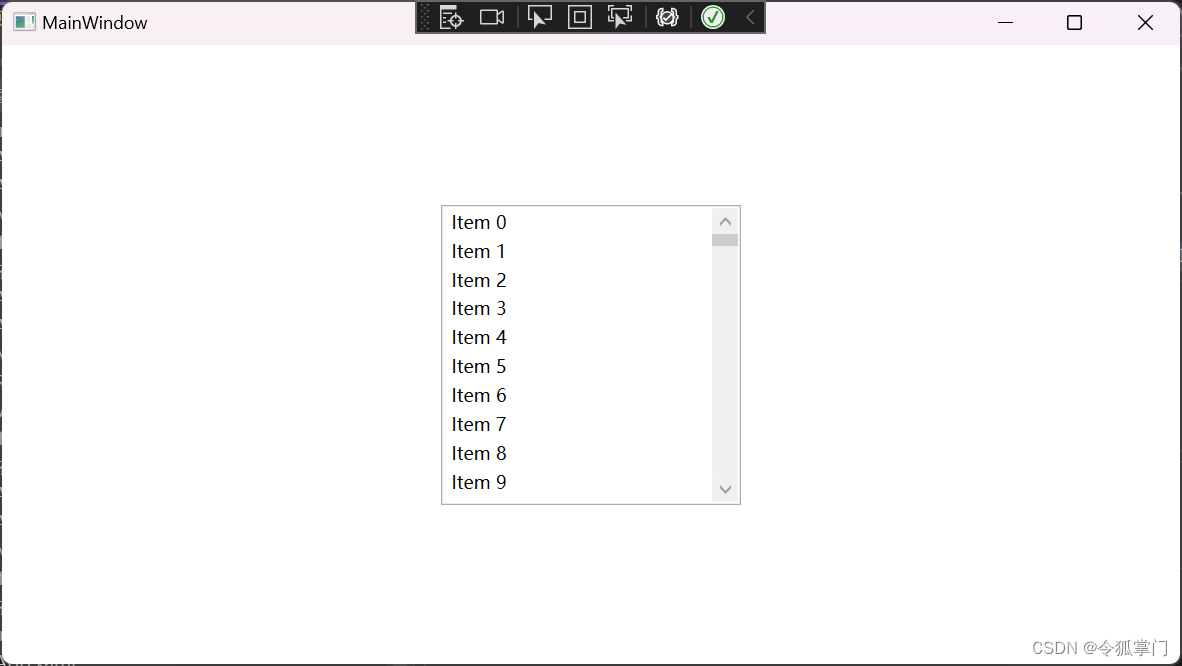
WPF中的虚拟化是什么
WPF(Windows Presentation Foundation)中的虚拟化是一种性能优化技术,它主要用于提高大量数据展示的效率。在WPF中,如果你有一个包含大量项的ItemsControl(例如ListBox、ListView或DataGrid等),…...

免费稳定几乎无门槛,我的ChartGPT助手免费分享给你
公众号「架构成长指南」,专注于生产实践、云原生、分布式系统、大数据技术分享。 概述 ChatGPT想必大家应该都不陌生了,大部分人或多或少都接触了,好多应该都是通过openAi的官方进行使用的,这个门槛对大部分人有点高,…...
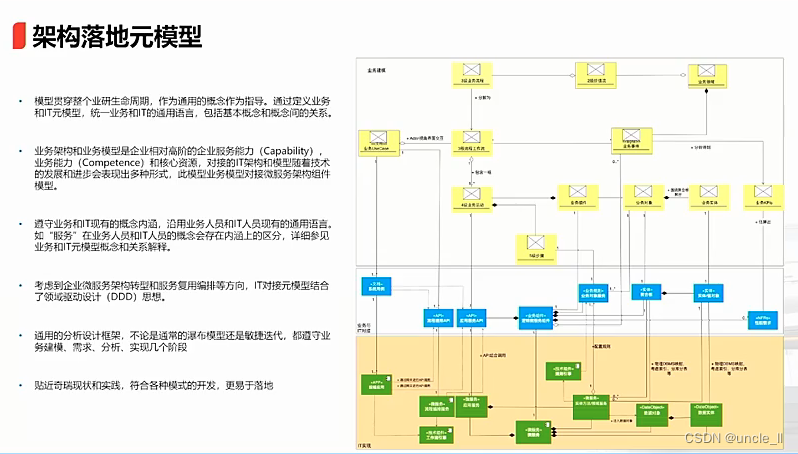
奇瑞金融:汽车金融行业架构设计
拆借联合贷款abs...

milvus数据库分区管理
一、创建分区 在创建集合时,会默认创建分区_default。 自己手动创建如下: from pymilvus import Collection collection Collection("book") # Get an existing collection. collection.create_partition("novel")二、检测分…...

pytorch.nn.Conv1d详解
通读了从论文中找的代码,终于找到这个痛点了! 以下详解nn.Conv1d方法 1 参数说明 in_channels(int) – 输入信号的通道。 out_channels(int) – 卷积产生的通道。 kernel_size(int or tuple) - 卷积核的尺寸,经测试后卷积核的大小应为in_cha…...
大数据HCIE成神之路之数学(2)——线性代数
线性代数 1.1 线性代数内容介绍1.1.1 线性代数介绍1.1.2 代码实现介绍 1.2 线性代数实现1.2.1 reshape运算1.2.2 转置实现1.2.3 矩阵乘法实现1.2.4 矩阵对应运算1.2.5 逆矩阵实现1.2.6 特征值与特征向量1.2.7 求行列式1.2.8 奇异值分解实现1.2.9 线性方程组求解 1.1 线性代数内…...
——使用ffmepg实现视音频解码)
音视频学习(十八)——使用ffmepg实现视音频解码
视频解码 初始化 视频常用的编解码器id定义(以h264和h265为例) // 定义在ffmpeg\include\libavcodec\avcodec.h AV_CODEC_ID_H264 AV_CODEC_ID_H265查找解码器:根据编解码id查看解码器 AVCodec* pCodecVideo avcodec_find_decoder(codec…...

nginx的GeoIP模块
使用场景 过滤指定地区/国家的IP,一般是国外IP禁止请求。 使用geoip模块实现不同国家的请求被转发到不同国家的nginx服务器,也就是根据国家负载均衡。 前置知识 GeoIP是什么? 官网地址 https://www.maxmind.com/en/home包含IP地址的地理位…...

mac控制台命令小技巧
shigen日更文章的博客写手,擅长Java、python、vue、shell等编程语言和各种应用程序、脚本的开发。记录成长,分享认知,留住感动。 hello伙伴们,作为忠实的mac骨灰级别的粉丝,它真的给我带来了很多效率上的提升。那作为接…...

Postman:API测试之Postman使用完全指南
Postman是一个可扩展的API开发和测试协同平台工具,可以快速集成到CI/CD管道中。旨在简化测试和开发中的API工作流。 Postman工具有Chrome扩展和独立客户端,推荐安装独立客户端。 Postman有个workspace的概念,workspace分personal和team类型…...

Flume学习笔记(3)—— Flume 自定义组件
前置知识: Flume学习笔记(1)—— Flume入门-CSDN博客 Flume学习笔记(2)—— Flume进阶-CSDN博客 Flume 自定义组件 自定义 Interceptor 需求分析:使用 Flume 采集服务器本地日志,需要按照日志…...

go的字符切片和字符串互转
Go 1.21 // 返回一个Slice,它的底层数组自ptr开始,长度和容量都是len func Slice(ptr *ArbitraryType, len IntegerType) []ArbitraryType // 返回一个指针,指向底层的数组 func SliceData(slice []ArbitraryType) *ArbitraryType // 生成一…...

所见即所得的动画效果:Animate.css
我们可以在集成Animate.css来改善界面的用户体验,省掉大量手写css动画的时间。 官网:Animate.css 使用 1、安装依赖 npm install animate.css --save2、引入依赖 import animate.css;3、在项目中使用 在class类名上animate__animated是必须的&#x…...
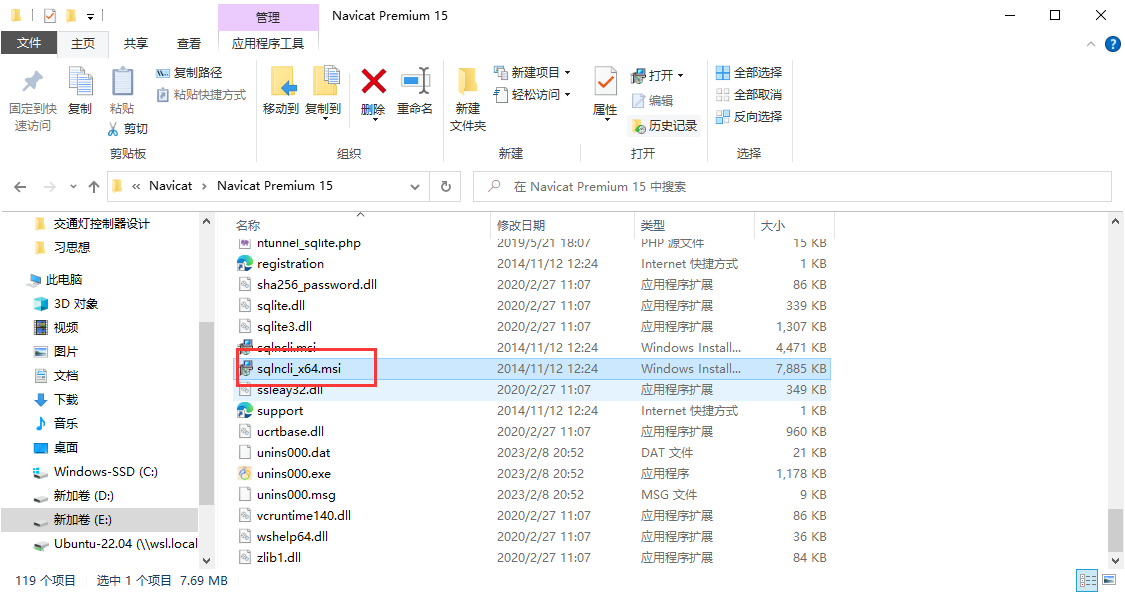
ERR:Navicat连接Sql Server报错
错误信息:报错:未发现数据源名称并且未指定默认驱动程序。 原因:Navicat没有安装Sqlserver驱动。 解决方案:在Navicat安装目录下找到sqlncli_x64.msi安装即可。 一键安装即可。 Navicat链接SQL Server配置 - MarchXD - 博客园 …...
python算法例10 整数转换为罗马数字
1. 问题描述 给定一个整数,将其转换为罗马数字,要求返回结果的取值范围为1~3999。 2. 问题示例 4→Ⅳ,12→Ⅻ,21→XⅪ,99→XCIX。 3. 代码实现 def int_to_roman(num):val [1000, 900, 500, 400,100, 90, 50, 40…...
springboot引入第三方jar包放到项目目录中,添加web.xml
参考博客:https://www.cnblogs.com/mask-xiexie/p/16086612.html https://zhuanlan.zhihu.com/p/587605618 1、在resources目录下新建lib文件夹,将jar包放到lib文件夹中 2、修改pom.xml文件 <dependency><groupId>com.lanren312</grou…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...