基于一致性算法的微电网分布式控制MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠)
本模型主要是基于一致性理论的自适应虚拟阻抗、二次电压补偿以及二次频率补偿,实现功率均分,保证电压以及频率稳定性。
一致性算法
分布式一致性控制主要分为两类:协调同步和跟踪同步。所谓协调同步是指将系统各个节点的某个控制目标同步到一个未规定或不可控的相同值,也称无领导者的一致性控制。跟踪同步控制是有领导者的一致性控制,其最终目的是将系统的其他各个节点的某个控制目标追踪到领导者状态,即向领导者看齐。对于本节要介绍的无功分配一致性控制采用的是无领导者的协调同步一致性控制。
分布式协同控制是通过建立稀疏通信网络的有向图实现的。将信息状态xi分配到通信节点i 上,每个节点都需要获取自身信息以及有向图上相邻节点的信息以更新其状态xi,基于连续一致性算法根据不同一致性控制采用不同更新规则。
针对协调同步问题,采用无领导者的一致性算法:
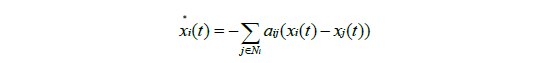
针对跟踪同步问题,采用有领导者的一致性算法:
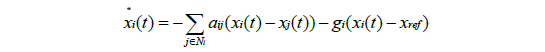
在分析功率分配问题时,需要把系统中所有节点的状态量niQi同步到一个未规定的共同值,因此,这里采用无领导者的一致性算法。
基于一致性算法的自适应虚拟阻抗控制
为了实现无功功率按比例分配,需要把系统中所有节点的状态量niQi同步到一个未规定的共同值,是一阶线性多智能体系统的协调同步问题。
![]()
其中, UQi是一个辅助控制,根据一致性控制协议,辅助控制是根据每一台DG 的自身信息和有向图中与其相邻的DG 信息得到的,即每一台DG 的无功功率控制器将本地无功分配信息与相邻的无功分配信息进行比较得到无功不匹配。
![]()
其中,cQ 是控制增益,eQi 为同步误差,即i 节点与相邻节点的无功分配误差
![]()
aij是邻接矩阵AG的元素, AG反映了通信网络的状态,如果通信网络发生变化,则AG 也会随之变化。
无功功率分配误差通过辅助控制uQ反馈到一个比例积分(PI)控制器,得到虚拟阻抗矫正项。虚拟阻抗矫正项动态更新虚拟阻抗的值。
![]()
如果各DG 的输出无功不能按各自的额定无功成比例分配,则通过分布式通信网络获取相邻DG 的无功分配信息,以更新本地的无功分配误差按照下式自适应地调节自身的虚拟电感。
![]()
同时采用自适应虚拟电阻可对微电网系统提供一定的阻尼效果
![]()
需要注意的是,这种方法不是直接调节每个DG 的无功功率,而是将每个DG 的虚拟阻抗调整到一个值,并且使得各DG 的等效阻抗与无功功率成反比,以消除由于线路阻抗不匹配所造成的无功功率分配误差。

基于一致性算法的二次电压补偿
电压恢复二次控制是将各DG 的参考电压幅值Vfi 同步到参考值 Vfref ,属于跟踪同步问题,故uvi 是根据有领导者的跟踪同步一致性算法确定的:

而Vfref 是根据公共母线电压Vpcc 和其参考电压Vref pcc 通过一个 PI 控制器确定的。
![]()
基于一致性算法的二次频率补偿
二次频率补偿类似于二次电压补偿
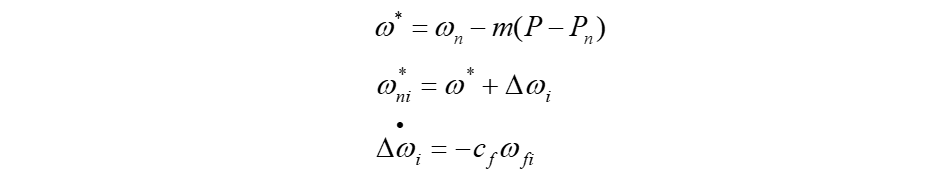
cf是控制增益,wfi用来实现频率控制的跟踪误差。

由公共母线参考频率wPCC和参考电压wPCCref通过PI控制后得到wfref。

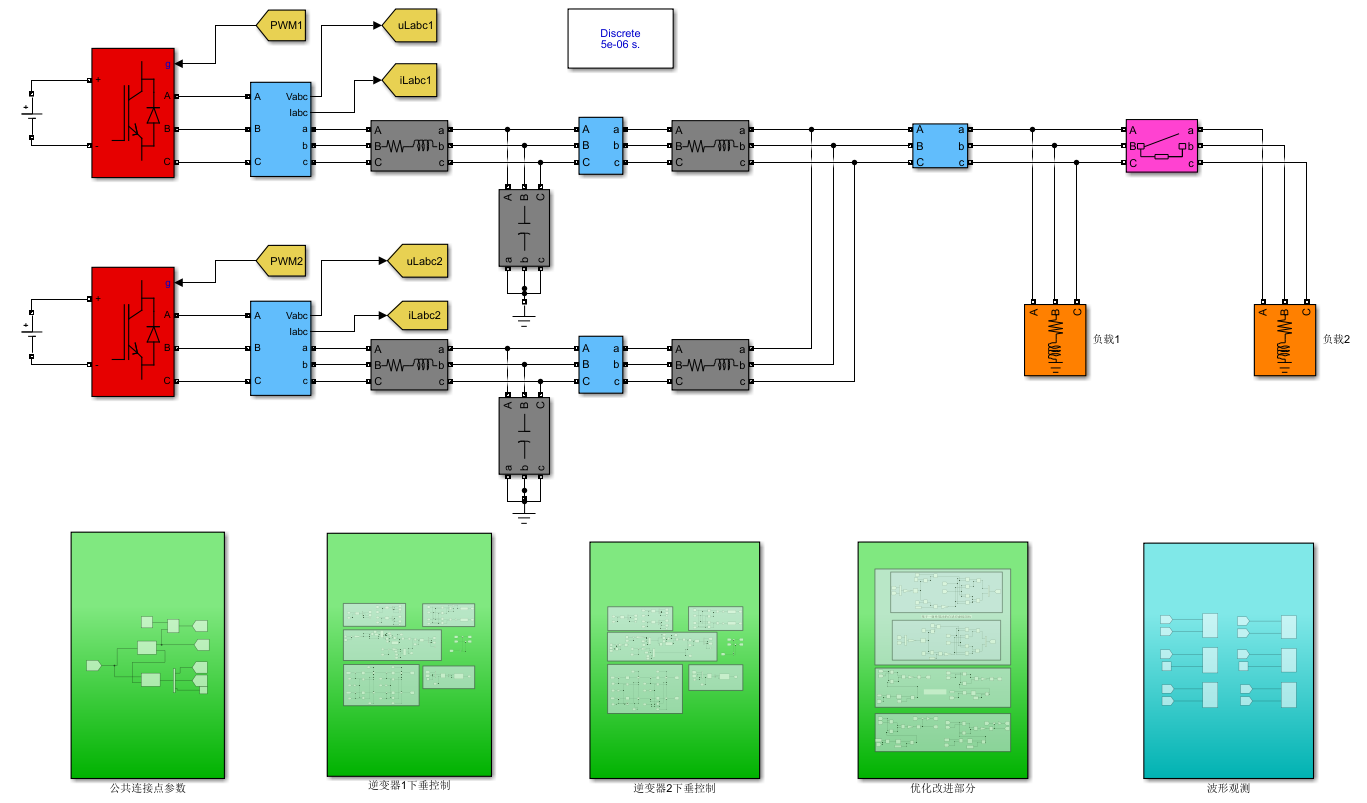
仿真主体模型:
优化控制部分:

功率输出波形:
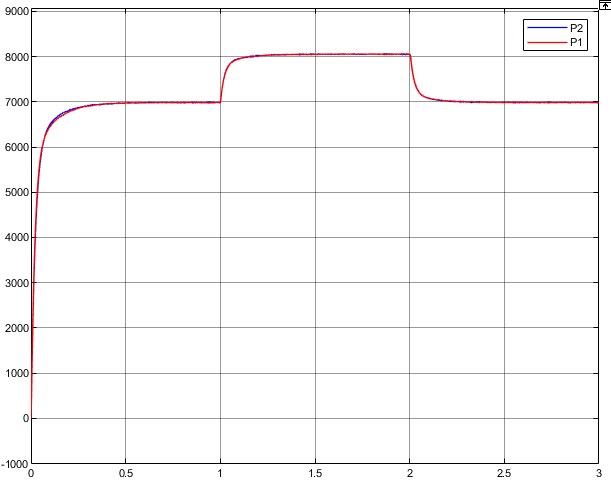

因为自适应虚拟阻抗的加入,有功、无功都能达到均分效果。
电压补偿:


上图为没有加入二次电压补偿的公共点电压,下图为加入二次补偿后的效果。因为二次电压补偿后,公共点电压不会因为虚拟阻抗的引入而导致电压跌落,快速回复到稳定值。
频率补偿:

上图为没有加入二次频率补偿的公共点电压,下图为加入二次频率补偿后的效果。因为二次频率补偿后,频率会稳定在50Hz,增加了系统的稳定性。
参考文献:
基于一致性理论的孤岛微电网分布式控制策略研究_熊德超
微电网中分布式电源改进下垂控制研究_曾信毅
相关文章:

基于一致性算法的微电网分布式控制MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 本模型主要是基于一致性理论的自适应虚拟阻抗、二次电压补偿以及二次频率补偿,实现功率均分,保证电压以及频率稳定性。 一致性算法 分布式一致性控制主要分为两类:协调同…...

Android 10.0 系统修改usb连接电脑mtp和PTP的显示名称
1.前言 在10.0的产品定制化开发中,在usb模块otg连接电脑,调整为mtp文件传输模式的时候,这时可以在电脑看到手机的内部存储 显示在电脑的盘符中,会有一个mtp名称做盘符,所以为了统一这个名称,就需要修改这个名称,接下来分析下处理的 方法来解决这个问题 2.系统修改usb连…...
飞鼠异地组网工具实战之访问k8s集群内部服务
飞鼠异地组网工具实战之访问k8s集群内部服务 一、飞鼠异地组网工具介绍1.1 飞鼠工具简介1.2 飞鼠工具官网 二、本次实践介绍2.1 本次实践场景描述2.2 本次实践前提2.3 本次实践环境规划 三、检查本地k8s集群环境3.1 检查k8s各节点状态3.2 检查k8s版本3.3 检查k8s系统pod状态 四…...
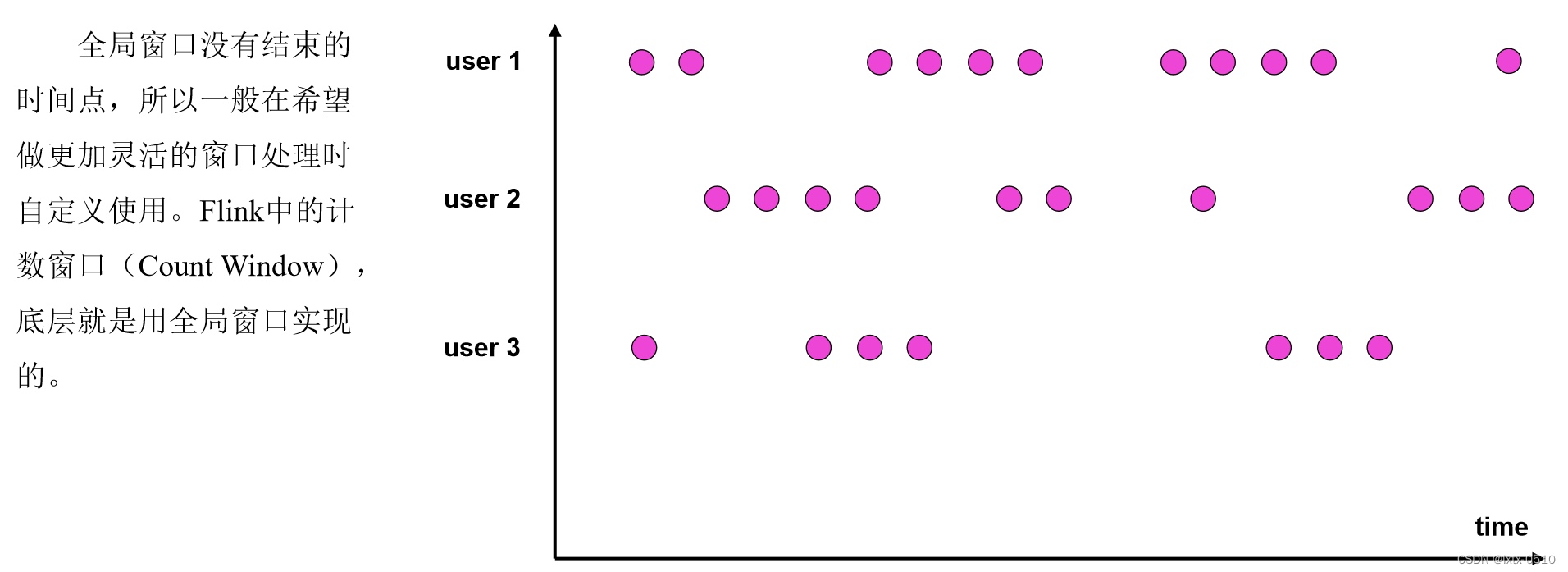
【Flink】窗口(Window)
窗口理解 窗口(Window)是处理无界流的关键所在。窗口可以将数据流装入大小有限的“桶”中,再对每个“桶”加以处理。 本文的重心将放在 Flink 如何进行窗口操作以及开发者如何尽可能地利用 Flink 所提供的功能。 对窗口的正确理解ÿ…...
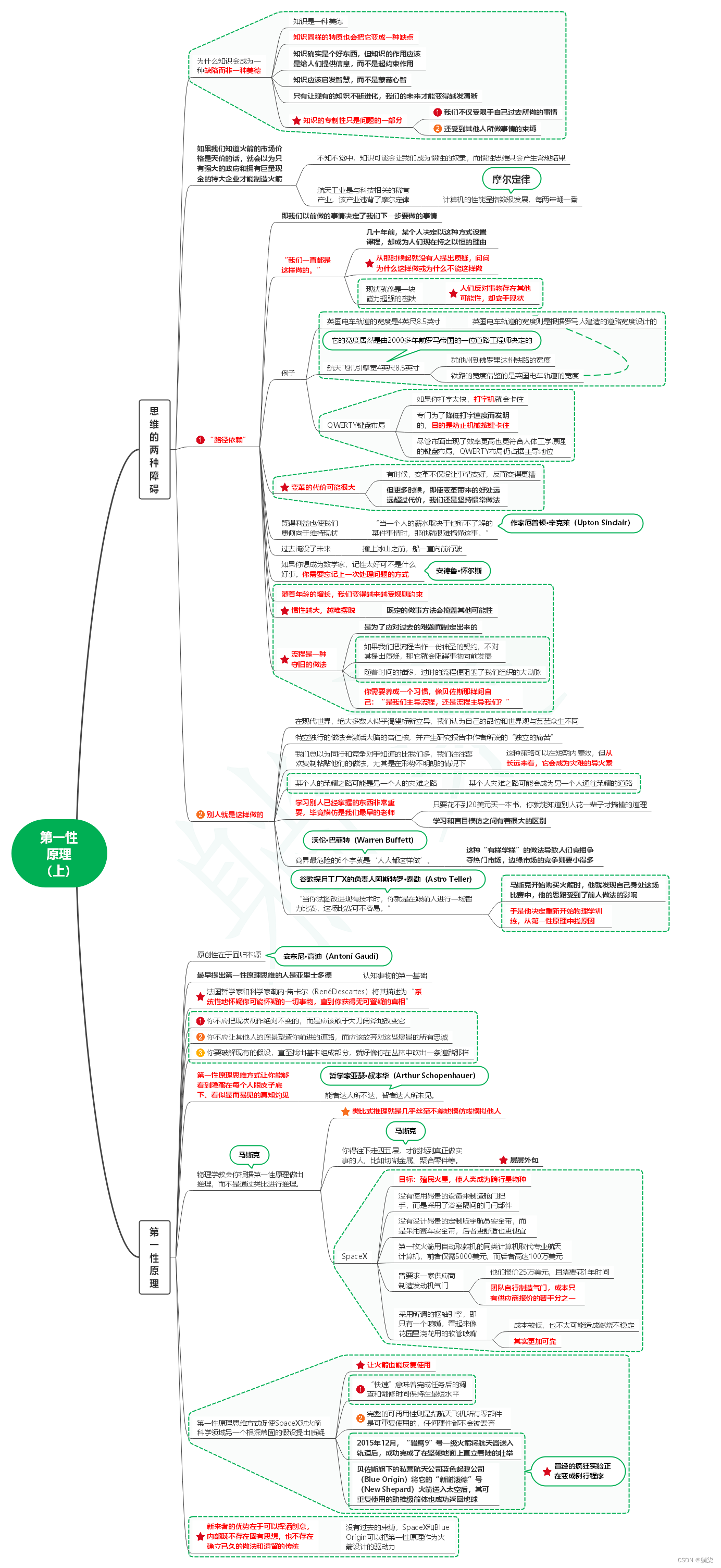
读像火箭科学家一样思考笔记03_第一性原理(上)
1. 思维的两种障碍 1.1. 为什么知识会成为一种缺陷而非一种美德 1.1.1. 知识是一种美德 1.1.2. 知识同样的特质也会把它变成一种缺点 1.1.3. 知识确实是个好东西,但知识的作用应该是给人们提供信息,而不是起约束作用 1.1.4. 知识应该启发智慧&#…...

npm私有云
安装node时npm会自动安装,npm也可以单独安装。 package.json 在使用npm时,package.json文件是非常重要的,因为它包含了关于项目的必要信息,比如名称、版本、依赖项等。在初始化新项目时,通常会使用npm init命令生成一…...

莹莹API管理系统源码附带两套模板
这是一个API后台管理系统的源码,可以自定义添加接口,并自带两个模板。 环境要求 PHP版本要求高于5.6且低于8.0,已测试通过的版本为7.4。 需要安装PHPSG11加密扩展。 已测试:宝塔/主机亲测成功搭建! 安装说明 &am…...

【Kingbase FlySync】命令模式:安装部署同步软件,实现KES到KES实现同步
【Kingbase FlySync】命令模式:安装部署同步软件,实现KES到KES实现同步迁移 概述准备环境目标资源1.测试虚拟机下载地址包含node1,node22.同步工具下载地址3.临时授权下载地址4.ruby工具下载地址5.EXAMv0.11.sql下载地址 实操:同步软件安装部署1.node1准…...
python使用selenium webDriver时 报错
可能原因和解决: 1. python 解释器 ----> 设置 2. 浏览器版本 与 浏览器驱动版本不一致 ----> 安装同一版本的 (下载chromedriver | 谷歌驱动更高版本的测试版) 参考:Python使用Selenium WebDriver的入门介绍及安装教程-CSDN博客 Selenium安…...

【ROS2机器人入门到实战】
ROS2机器人入门到实战教程(鱼香ROS) 写在前面 当前平台文章汇总地址:ROS2机器人从入门到实战获取完整教程及配套资料代码,请关注公众号<鱼香ROS>获取教程配套机器人开发平台:两驱版| 四驱版为方便交流,搭建了机器人技术问…...

Nuxt3框架局部文件引用外部JS/CSS文件的相关配置方法
引入外部JS: <script setup>useHead({script: [ {type: "text/javascript",src: https://cdnjs.cloudflare.com/ajax/libs/jquery/3.7.0/jquery.min.js}]}) </script>useHead只能与组件的setup和生命周期钩子一起使用 如果需要将js放置body区…...
Docker 可视化面板 ——Portainer
Portainer 是一个非常好用的 Docker 可视化面板,可以让你轻松地管理你的 Docker 容器。 官网:Portainer: Container Management Software for Kubernetes and Docker 【Docker系列】超级好用的Docker可视化工具——Portainer_哔哩哔哩_bilibili 环境 …...

Java 教育局民办教育信息服务与监管平台
1) 项目背景 按照《中华人民共和国民办教育促进法》和《中华人民共和国政府信息公开条例》的相关规定,为满足学生和家长、社会各界获取权威信息的需求,着力解决服务老百姓最后一公里问题,达到宣传民办教育和引导家长择校的效果࿰…...
小迪笔记(1)——操作系统文件下载反弹SHELL防火墙绕过
名词解释 POC:验证漏洞存在的代码; EXP:利用漏洞的代码; payload:漏洞利用载荷, shellcode:漏洞代码, webshell:特指网站后门; 木马:强调控制…...

Pytorch D2L Subplots方法对画图、图片处理
问题代码 def show_images(imgs, num_rows, num_cols, titlesNone, scale1.5): #save """绘制图像列表""" figsize (num_cols * scale, num_rows * scale) _, axes d2l.plt.subplots(num_rows, num_cols, figsizefigsize) axes axes.flatten…...
)
MATLAB算法实战应用案例精讲-【目标检测】YOLOV5(补充篇)
目录 算法原理 YOLOv5数据集训练 软硬件背景: 数据集准备 配置文件 模型训练...

WPF中可视化树和逻辑树的区别是什么
在WPF中,用户界面元素被组织成树形结构。这种结构主要分为两种:逻辑树(Logical Tree)和可视化树(Visual Tree)。它们在设计上各有特点和用途。 逻辑树(Logical Tree) 逻辑树是WPF中…...
——web应用架构搭建漏洞HTTP数据包代理服务器)
小迪安全笔记(2)——web应用架构搭建漏洞HTTP数据包代理服务器
Web应用环境架构类 开发语言:php、java、python、ASP、ASPX等程序源码:用的人多了,就成CMS了。中间件容器:IIS、Apache、Nginx、Tomcat、Weblogic、Jboos、glasshfish等数据库类型:Access、Mysql、Mssql、Oracle、Redi…...

[AI]ChatGPT4 与 ChatGPT3.5 区别有多大
ChatGPT 3.5 注册已经不需要手机了,直接邮箱认证就可以,这可真算是好消息,坏消息是 ChatGPT 4 还是要收费。 那么 GPT-3.5 与 GPT-4 区别有多大呢,下面简单测试一下。 以从 TDengine 订阅数据为例,TDengine 算是不太小…...

node实战——koa实现文件上传
文章目录 ⭐前言⭐koa实现文件上传⭐foxapi测试⭐总结⭐结束⭐前言 大家好,我是yma16,本文分享关于node实战——node实战——koa实现文件上传。 本文适用对象:前端初学者转node方向,在校大学生,即将毕业的同学,计算机爱好者。 node系列往期文章 node_windows环境变量配置…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
