C++二分查找算法:找到 Alice 和 Bob 可以相遇的建筑
本文涉及的基础知识点
二分查找算法合集
离线查询
题目
给你一个下标从 0 开始的正整数数组 heights ,其中 heights[i] 表示第 i 栋建筑的高度。
如果一个人在建筑 i ,且存在 i < j 的建筑 j 满足 heights[i] < heights[j] ,那么这个人可以移动到建筑 j 。
给你另外一个数组 queries ,其中 queries[i] = [ai, bi] 。第 i 个查询中,Alice 在建筑 ai ,Bob 在建筑 bi 。
请你能返回一个数组 ans ,其中 ans[i] 是第 i 个查询中,Alice 和 Bob 可以相遇的 最左边的建筑 。如果对于查询 i ,Alice 和 Bob 不能相遇,令 ans[i] 为 -1 。
示例 1:
输入:heights = [6,4,8,5,2,7], queries = [[0,1],[0,3],[2,4],[3,4],[2,2]]
输出:[2,5,-1,5,2]
解释:第一个查询中,Alice 和 Bob 可以移动到建筑 2 ,因为 heights[0] < heights[2] 且 heights[1] < heights[2] 。
第二个查询中,Alice 和 Bob 可以移动到建筑 5 ,因为 heights[0] < heights[5] 且 heights[3] < heights[5] 。
第三个查询中,Alice 无法与 Bob 相遇,因为 Alice 不能移动到任何其他建筑。
第四个查询中,Alice 和 Bob 可以移动到建筑 5 ,因为 heights[3] < heights[5] 且 heights[4] < heights[5] 。
第五个查询中,Alice 和 Bob 已经在同一栋建筑中。
对于 ans[i] != -1 ,ans[i] 是 Alice 和 Bob 可以相遇的建筑中最左边建筑的下标。
对于 ans[i] == -1 ,不存在 Alice 和 Bob 可以相遇的建筑。
示例 2:
输入:heights = [5,3,8,2,6,1,4,6], queries = [[0,7],[3,5],[5,2],[3,0],[1,6]]
输出:[7,6,-1,4,6]
解释:第一个查询中,Alice 可以直接移动到 Bob 的建筑,因为 heights[0] < heights[7] 。
第二个查询中,Alice 和 Bob 可以移动到建筑 6 ,因为 heights[3] < heights[6] 且 heights[5] < heights[6] 。
第三个查询中,Alice 无法与 Bob 相遇,因为 Bob 不能移动到任何其他建筑。
第四个查询中,Alice 和 Bob 可以移动到建筑 4 ,因为 heights[3] < heights[4] 且 heights[0] < heights[4] 。
第五个查询中,Alice 可以直接移动到 Bob 的建筑,因为 heights[1] < heights[6] 。
对于 ans[i] != -1 ,ans[i] 是 Alice 和 Bob 可以相遇的建筑中最左边建筑的下标。
对于 ans[i] == -1 ,不存在 Alice 和 Bob 可以相遇的建筑。
参数范围:
1 <= heights.length <= 5 * 104
1 <= heights[i] <= 109
1 <= queries.length <= 5 * 104
queries[i] = [ai, bi]
0 <= ai, bi <= heights.length - 1
分析
时间复杂度
时间复杂度(nlogm),枚举queries时间复杂度O(n),处理单个查询时间复杂度O(logm)。n和queries的长度,m是heights的长度。
分情况讨论
无需考虑一个人跳两次及以上的情况。假定跳了两次: i1->i2->i3,那说明i1<i2,i2<i3,也就是i1<i3,那直接跳到i3就可以了。
三种情况:
| 两人都不跳,初始位置相同 | |
| 一人直接跳到另外一个人处 | |
| 两个人都跳 |
两个人都跳
假定两人的最大位置是iMaxIndex,两人的最大高度是iMaxHeight。heights(iMaxIndex…]中寻找大于iMaxHeight的组合, 如果存在多个组合,返回最小的索引。
mHeightIndexs的key是高度,value是索引。如果key1 >= key0,且value1 <= value0,那key0被淘汰。
淘汰后,key和value都升序。
离线查询
如果iMaxIndex是按降序排列,那么mHeightIndexs每个元素只需要插入一次。
代码
核心代码
class Solution {
public:
vector leftmostBuildingQueries(vector& heights, vector<vector>& queries) {
m_c = queries.size();
vector indexs;
for (int i = 0; i < m_c; i++)
{
indexs.emplace_back(i);
}
sort(indexs.begin(), indexs.end(), [&](const int& i1, const int& i2)
{
return max(queries[i1][0], queries[i1][1]) > max(queries[i2][0], queries[i2][1]);
});
COrderValueMap<int,int,true,true> mHeightIndexs;
vector vRet(m_c, -1);
int iHeightIndex = heights.size() - 1;
for (int inx :indexs)
{
const int iMinIndex = min(queries[inx][0], queries[inx][1]);
const int iMaxIndex = max(queries[inx][0], queries[inx][1]);
if (iMinIndex == iMaxIndex) {
vRet[inx] = iMaxIndex;
continue;
}
if (heights[iMinIndex] < heights[iMaxIndex])
{
vRet[inx] = iMaxIndex;
continue;
}
const int iMaxHeight = max(heights[queries[inx][0]], heights[queries[inx][1]]);
while (iHeightIndex > iMaxIndex)
{
mHeightIndexs.Add(heights[iHeightIndex], iHeightIndex);
iHeightIndex–;
}
auto it = mHeightIndexs.m_map.upper_bound(iMaxHeight);
if (mHeightIndexs.m_map.end() != it)
{
vRet[inx] = it->second;
}
}
return vRet;
}
int m_c;
};
测试用例
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
Assert(v1[i], v2[i]);
}
}
int main()
{
vectorheights;
vector<vector> queries;
int k;
vector res;
{
Solution slu;
heights = {6, 4, 8, 5, 2, 7};
queries = { {0, 1}, { 0,3 }, { 2,4 }, { 3,4 }, { 2,2 }};
res = slu.leftmostBuildingQueries(heights, queries);
//Assert(1, res);
}
//CConsole::Out(res);
}
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨子曰:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
相关文章:

C++二分查找算法:找到 Alice 和 Bob 可以相遇的建筑
本文涉及的基础知识点 二分查找算法合集 离线查询 题目 给你一个下标从 0 开始的正整数数组 heights ,其中 heights[i] 表示第 i 栋建筑的高度。 如果一个人在建筑 i ,且存在 i < j 的建筑 j 满足 heights[i] < heights[j] ,那么这个…...

建立跨层全栈的区块链安全保障系统-应用层,系统层,设施层
目录 建立跨层全栈的区块链安全保障系统 应用层 系统层 设施层...
程序员告诉你:人工智能是什么?
随着科技的快速发展,人工智能这个词汇已经逐渐融入了我们的日常生活。然而,对于大多数人来说,人工智能仍然是一个相对模糊的概念。 首先,让我们从人工智能的定义开始。人工智能是一种模拟人类智能的技术,它涵盖了多个领…...
飞书开发学习笔记(七)-添加机器人及发送webhook消息
飞书开发学习笔记(七)-添加机器人及发送webhook消息 一.添加飞书机器人 1.1 添加飞书机器人过程 在群的右上角点击折叠按键…选择 设置 群机器人中选择 添加机器人 选择自定义机器人,通过webhook发送消息 弹出的信息中有webhook地址,选择复制。 安…...

C/C++统计数 2021年12月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C统计数 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C统计数 2021年12月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 给定一个数的序列S,以及一个区间[L, R], 求序列…...
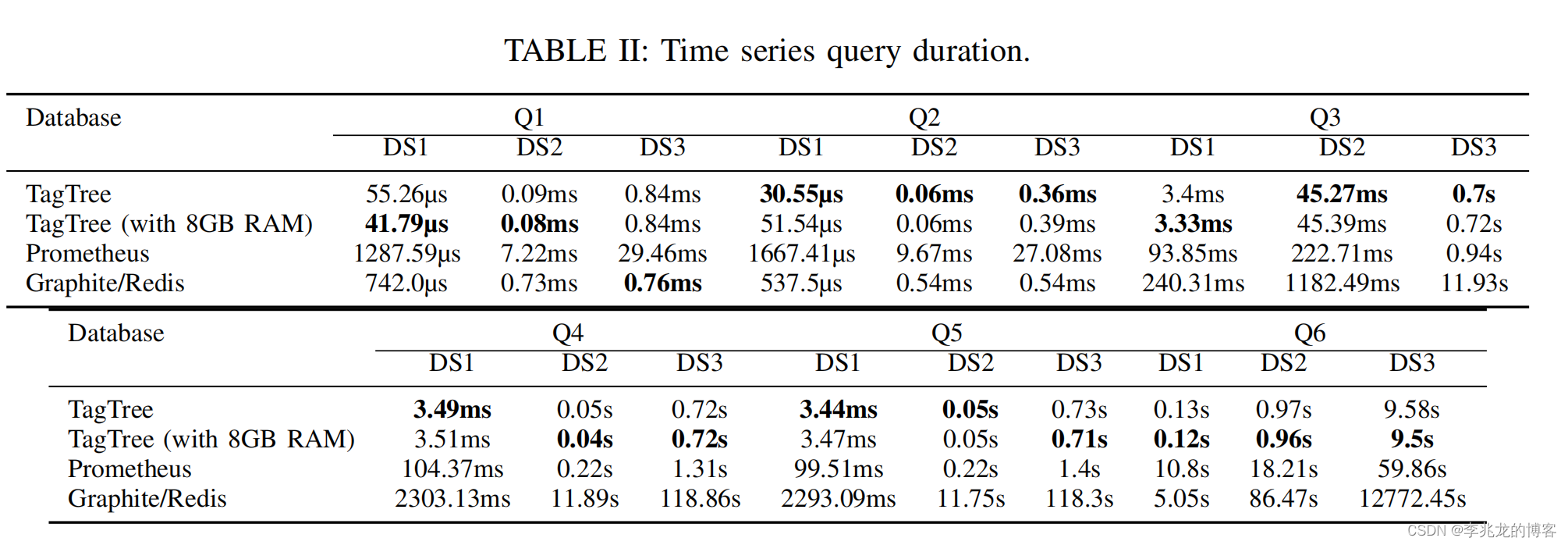
从一到无穷大 #19 TagTree,倒排索引入手是否是优化时序数据库查询的通用方案?
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 本作品 (李兆龙 博文, 由 李兆龙 创作),由 李兆龙 确认,转载请注明版权。 文章目录 文章主旨时序数据库查询的一般流程扫描维度聚合时间聚合管控语句 TagTree整体结构索引…...

程序员带你入门人工智能
随着人工智能技术的飞速发展,越来越多的程序员开始关注并学习人工智能。作为程序员,我们可能会对如何开始了解人工智能感到困惑。今天,我将向大家介绍一些如何通过自学了解人工智能的经验和方法,帮助大家更好地入门这个充满挑战和…...

机器学习笔记 - 了解常见开源文本识别数据集以及了解如何创建用于文本识别的合成数据
一、部分开源数据集 以下是一些英文可用的开源文本识别数据集。 ICDAR 数据集:ICDAR 代表国际文档分析和识别会议。该活动每两年举行一次。他们带来了一系列塑造了研究社区的场景文本数据集。例如, ICDAR-2013和ICDAR-2015数据集。 MJSynth 数据集:该合成词数据集由牛津大…...

openssl开发详解
文章目录 一、openssl 开发环境二、openssl随机数生成三、openssl对称加密3.1 SM43.2 AES3.3 DES3.4 3DES 四、openssl非对称加密4.1 SM24.2 RSA4.3 ECC 五、openssl的hash5.1 SM35.2 md55.3 sha256 五、证书5.1 证书格式 六、openssl网络编程七、openssl调试FIDO流程 一、open…...

conda虚拟环境中安装的cuda和服务器上安装的cuda的异同
服务器上已安装Nvidia提供的cuda,nvcc -V时会出现已安装的CUDA版本。如下图所示,服务器上已安装好的cuda版本为10.1。 但是当我们在Anaconda虚拟环境下安装pytorch或者paddlepaddle等深度学习框架的GPU版本时,通常会选择较高版本的cuda&…...

股东入股可用的出资形式主要有哪些
股东入股,可用的出资形式主要包括货币以及实物、知识产权、土地使用权等可以用货币估价并可以依法转让的非货币财产。 第一,货币。设立公司必然需要一定数量的流动资金。以支付创建公司时的开支和启动公司运营。因此,股东可以用货币出资。 第…...

react中设置activeClassName的笔记
React是一种流行的JavaScript库,用于构建动态用户界面。它具有许多有用的组件,其中之一是NavLink组件。NavLink组件用于在React应用程序中创建链接,并且它具有许多有用的属性,例如选中的样式设置。 react-router-dom": “^6…...

JS原型对象prototype
让我简单的为大家介绍一下原型对象prototype吧! 使用原型实现方法共享 1.构造函数通过原型分配的函数是所有对象所 共享的。 2.JavaScript 规定,每一个构造函数都有一个 prototype 属性,指向另一个对象,所以我们也称为原型对象…...
nodejs+vue实验室上机管理系统的设计与实现-微信小程序-安卓-python-PHP-计算机毕业设计
用户:管理员、教师、学生 基础功能:管理课表、管理机房情况、预约机房预约;权限不同,预约类型不同,教师可选课堂预约和个人;课堂预约。 在实验室上机前,实验室管理员需要对教务处发来的上机课表…...

SpringBoot 注解开发
利用自定义注解,解决问题 例1 自定义注解限制请求 场景:前端发起的频繁的请求,导致服务器压力过大。需要对后端接口进行限流处理,每个接口都需要做限流处理的话就会导致代码冗余,此时就可以利用注解进行解决 非注解形…...
使用持久卷部署 WordPress 和 MySQL
🗓️实验环境 OS名称Microsoft Windows 11 家庭中文版系统类型x64-based PCDocker版本Docker version 24.0.6, build ed223bcminikube版本v1.32.0 🖇️创建 kustomization.yaml 你可以通过 kustomization.yaml 中的生成器创建一个 Secret存储密码或密…...

2024年csdn最新最全的Postman接口测试: postman实现参数化
什么时候会用到参数化 比如:一个模块要用多组不同数据进行测试 验证业务的正确性 Login模块:正确的用户名,密码 成功;错误的用户名,正确的密码 失败 postman实现参数化 在实际的接口测试中,部分参数…...
开发知识点-uniapp微信小程序-开发指南
uniapp Vue的原型链生命周期函数onLoaduni.chooseLocationgetCurrentPages美团外卖微信小程序开发uniapp-美团外卖微信小程序开发P1 成果展示P2外卖小程序后端,学习给小程序写http接口P3 主界面配置P4 首页组件拆分P13 外卖列表布局筛选组件商家 布局测试数据创建样…...

Vue3+Vite实现工程化,事件绑定以及修饰符
我们可以使用v-on来监听DOM事件,并在事件触发时执行对应的Vue的Javascript代码。 用法:v-on:click "handler" 或简写为 click "handler"vue中的事件名原生事件名去掉 on 前缀 如:onClick --> clickhandler的值可以是方法事件…...

20、动态路由_下滑线为前缀的目录
创建文件 pages_question\index.vue pages_question\detail.vue 生成的对应路由: const _6bf6ece8 () > interopDefault(import(..\\pages\\_question\\index.vue /* webpackChunkName: "pages/_question/index" */)) const _a98c80aa () > in…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
