【算法挨揍日记】day31——673. 最长递增子序列的个数、646. 最长数对链
673. 最长递增子序列的个数
673. 最长递增子序列的个数
题目解析:
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。
注意 这个数列必须是 严格 递增的。
解题思路:
解题代码:
class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n=nums.size();vector<int>dp(n,1);vector<int>f(n,1);int retlength=1;int retcount=1;for(int i=1;i<n;i++){//int length=f[0];//0到i-1区间内的最大长度for(int j=0;j<i;j++){if(nums[j]<nums[i]){ if(f[j]+1==f[i])dp[i]+=dp[j];else if(f[j]+1>f[i]){dp[i]=dp[j];f[i]=f[j]+1;}} }if(retlength==f[i])retcount+=dp[i];else if(retlength<f[i]){retcount=dp[i];retlength=f[i];}}return retcount; }
};646. 最长数对链
646. 最长数对链
题目描述:
给你一个由 n 个数对组成的数对数组 pairs ,其中 pairs[i] = [lefti, righti] 且 lefti < righti 。
现在,我们定义一种 跟随 关系,当且仅当 b < c 时,数对 p2 = [c, d] 才可以跟在 p1 = [a, b] 后面。我们用这种形式来构造 数对链 。
找出并返回能够形成的 最长数对链的长度 。
你不需要用到所有的数对,你可以以任何顺序选择其中的一些数对来构造。
解题思路:
解题代码:
class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) {sort(pairs.begin(),pairs.end());int n=pairs.size();vector<int>dp(n,1);for(int i=1;i<n;i++){for(int j=0;j<i;j++){if(pairs[j][1]<pairs[i][0])dp[i]=max(dp[i],dp[j]+1);}}int ret=1;for(int i=0;i<n;i++)ret=max(ret,dp[i]);return ret;}
};相关文章:

【算法挨揍日记】day31——673. 最长递增子序列的个数、646. 最长数对链
673. 最长递增子序列的个数 673. 最长递增子序列的个数 题目解析: 给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。 注意 这个数列必须是 严格 递增的。 解题思路: 算法思路: 1. 状态表⽰: 先尝试…...
Jmeter做接口测试
1.Jmeter的安装以及环境变量的配置 Jmeter是基于java语法开发的接口测试以及性能测试的工具。 jdk:17 (最新的Jeknins,只能支持到17) jmeter:5.6 官网:http://jmeter.apache.org/download_jmeter.cgi 认识JMeter的目录࿱…...

第14届蓝桥杯青少组python试题解析:23年5月省赛
选择题 T1. 执行以下代码,输出结果是()。 lst "abc" print(lstlst)abcabc abc lstlst abcabc T2. 执行以下代码,输出的结果是()。 age {16,18,17} print(type(sorted(age)))<class set&…...
SpringCloud 微服务全栈体系(十四)
第十一章 分布式搜索引擎 elasticsearch 四、RestAPI ES 官方提供了各种不同语言的客户端,用来操作 ES。这些客户端的本质就是组装 DSL 语句,通过 http 请求发送给 ES。官方文档地址:https://www.elastic.co/guide/en/elasticsearch/client/…...

【开题报告】基于微信小程序的个人健康管理系统的设计与实现
1.选题背景与意义 在现代社会,人们对健康的关注日益增加。随着生活方式的变化和工作压力的增加,许多人意识到保持良好的身体健康对于提高生活质量和幸福感的重要性。 然而,许多人在日常生活中缺乏对自身健康状况的了解和管理。他们可能没有…...

Swagger笔记
一、导包 <!--引入swagger--> <dependency><groupId>io.springfox</groupId><artifactId>springfox-swagger2</artifactId><version>2.9.2</version> </dependency> <!--前端的UI界面--> <dependency><…...
数据结构 堆
手写堆,而非stl中的堆 如何手写一个堆? //将数组建成堆 <O(n) for (int i n / 2;i;i--) //从n/2开始down down(i); 从n/2元素开始down,最下面一层元素的个数是n/2,其余上面的元素的个数是n/2,从最下面一层到最高层…...
将 ONLYOFFICE 文档编辑器与 Node.js 应用集成
我们来了解下,如何将 ONLYOFFICE 文档编辑器与您的 Web 应用集成。 许多 Web 应用都可以从文档编辑功能中获益。但是要从头开始创建这个功能,需要花费大量时间和精力。幸运的是,您可以使用 ONLYOFFICE——这是一款开源办公套件,可…...
CentOS 7搭建Gitlab流程
目录 1、查询docker镜像gitlab-ce 2、拉取镜像 3、查询已下载的镜像 4、新建gitlab文件夹 5、在gitlab文件夹下新建相关文件夹 6、创建运行gitlab的容器 7、查看docker容器 8、根据Linux地址访问gitlab 9、进入docker容器,设置用户名的和密码 10、登录git…...
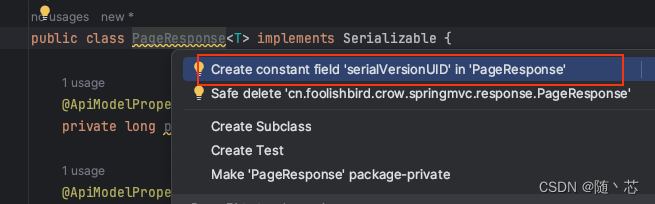
Idea安装完成配置
目录: 环境配置Java配置Maven配置Git配置 基础设置编码级设置File Header自动生成序列化编号配置 插件安装MyBtisPlusRestfulTooklkit-fix 环境配置 Java配置 Idea右上方,找到Project Settings. 有些版本直接有,有些是在设置下的二级菜单下…...

超详细~25考研规划~感恩现在努力的你!!!
25考研规划 俄语,翻译过来叫我爱你 考试时间 第一天 8.30-11.30政治——100分 2.00-5.00英语——100分 第二天 8.30-11.30数学——150分 2.00-5.00专业课——150分 1.什么是25考研 将在2024年12月参加考研,2025年本科毕业,9月读研究…...

智慧城市安全监控的新利器
在传统的城市管理中,井盖的监控一直是一个难题,而井盖异动传感器的出现为这一问题提供了有效的解决方案。它具有体积小、重量轻、安装方便等特点,可以灵活地应用于各种类型的井盖,实现对城市基础设施的全方位监控。 智能井盖监测终…...
)
【算法】石子合并(区间dp)
题目 设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子…...

C++-特殊类和单例模式
1.请设计一个类,不能被拷贝 拷贝构造函数以及赋值运算符重载,因此想要让一个类禁止拷贝,只需让该类不能调用拷贝构造函数以及赋值运算符重载即可。 //该类不能发生拷贝class NonCopy{public:NonCopy(const NonCopy& Nc) delete;NonCopy&…...

【开源】基于Vue.js的智能教学资源库系统
项目编号: S 050 ,文末获取源码。 \color{red}{项目编号:S050,文末获取源码。} 项目编号:S050,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课…...

C语言之qsort()函数的模拟实现
C语言之qsort()函数的模拟实现 文章目录 C语言之qsort()函数的模拟实现1. 简介2. 冒泡排序3. 对冒泡排序进行改造4. 改造部分4.1 保留部分的冒泡排序4.2 比较部分4.3 交换部分 5. bubble_sort2完整代码6. 使用bubble_sort2来排序整型数组7. 使用bubble_sort2来排序结构体数组7.…...

数字化未来:实时云渲染在智慧城市中的创新应用
数字中国战略"是国家推动数字经济发展的战略框架。这个战略旨在加速数字化转型,推动信息技术在各个领域的应用,提高社会经济效益和人民生活质量。而智慧城市作为其中的重要一环,重要性不言而喻。 智慧城市是当今城市发展的热点和趋势&a…...
Go语言常用命令详解(二)
文章目录 前言常用命令go bug示例参数说明 go doc示例参数说明 go env示例 go fix示例 go fmt示例 go generate示例 总结写在最后 前言 接着上一篇继续介绍Go语言的常用命令 常用命令 以下是一些常用的Go命令,这些命令可以帮助您在Go开发中进行编译、测试、运行和…...

ChatGPT 从零到一打造私人智能英语学习助手
近几年,随着智能化技术的发展和人工智能的兴起,越来越多的应用程序开始涌现出来。在这些应用中,语音识别、自然语言处理以及机器翻译等技术都得到了广泛的应用。其中,聊天机器人成为了最受欢迎的人工智能应用之一,它们…...
-盛最多水的容器)
算法升级之路(七)-盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 原题链接: 盛最多水的容器 解题思路&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
